预应力箱型梁桥遭受超高车辆在不同位置撞击下的动态响应

田　力，　冯振宁

(天津大学　建筑工程学院， 天津　300072)



预应力箱型梁桥遭受超高车辆在不同位置撞击下的动态响应

田力，冯振宁

(天津大学建筑工程学院， 天津300072)

摘要：随着城镇化的加快，超高车辆撞击城市预应力箱型桥梁上部结构的事故时有发生。因此，有必要对此类撞击事故的动态响应进行研究。运用LS-DYNA建立了精细化T型梁桥上部结构的三维分离式模型，与罐体模型进行碰撞分析。与相应试验结果进行了对比，验证了LS-DYNA模拟此类撞击的正确性。运用LS-DYNA建立了精细化预应力箱型梁桥上部结构的三维分离式模型，分别建立了三种工况下车辆与桥梁上部结构碰撞的耦合模型，由计算结果可以看出三种工况下桥梁损伤的位置和状况大致相似，撞击位置距离支座越近，桥梁损伤就越严重。结果表明：撞击位置距离支座越近，碰撞力越大，撞击区域位移就越大。因此，超高车辆撞击预应力箱梁考虑最不利情况时，应研究车辆撞击桥梁支座处的破坏情况。

关键词：箱型梁桥；汽车撞击；分离式模型；动态响应

在繁华的现代大都市中，运输繁忙的立交桥和其它一些跨线城市桥梁经常遭受超高车辆撞击，造成车辆和桥梁损伤。特别是最近二十年，随着中国经济技术的迅猛发展，城镇化进程的加快，越来越多的人们涌入大城市中，使得城市立体交通体系成为城市交通的重要组成部分。这一系列的变化改善了城市交通，方便人们的出行，但也致使超高车辆撞击城市桥梁上部结构的事故发生更加频繁。

尽管并非每次超高车辆撞击桥梁上部结构会造成车毁人亡的重大损失，但是桥梁被撞会使得城市交通受阻、桥梁寿命减少，造成一定的经济损失。因此，此类问题的频繁发生得到了社会多方面的重视。英国Arup公司曾经做过车撞桥梁上部结构的足尺实验，但并未公布实验结果。欧洲规范EUROCODE 1[1]对车撞桥梁上部结构提出了相关的撞击力计算方法，但对桥梁的动态响应没有具体研究。我国的JTG D60-2004《公路桥梁通用设计规范》[2]参考外国规范，简单规定汽车撞击力的等效撞击力大小取值(等效撞击力在车辆行驶方向取1000 kN，垂直车辆行驶方向取500 kN，两个方向不能同时考虑)，但是对于不同桥型、不同撞击位置，规范并没有详细划分。重庆交通大学的毕晨华等[3]对T型梁桥遭受超高车辆撞击的损伤进行有限元分析。清华大学陆新征等[4～6]对超高车辆撞击桥梁上部结构进行了一系列的数值模拟分析，研究了部分桥型的破坏过程和损坏机理，分析了各个桥梁遭受撞击后不同的动态响应。然而，对于预应力混凝土薄壁箱梁这一常见桥型的研究还没有涉及。而且，由于桥梁上部结构配筋的复杂性，目前研究桥梁上部结构多采用整体式建模。显然为了获取更精确的结果，建立分离式模型模拟超高车辆撞击桥梁上部结构显得十分必要。

本文运用有限元分析软件LS-DYNA对超高车辆撞击预应力箱型梁桥的过程进行了数值模拟。建立了精细化的预应力混凝土箱梁分离式模型，验证了该软件数值模拟的有效性，比较分析了汽车在不同撞击位置下，预应力混凝土桥梁的动态响应。

1数值模型和材料

1.1汽车数值模型

作为美国政府部门汽车安全的最高主管部门，美国高速公路安全管理局(NHTSA)在汽车碰撞实验分析和汽车安全性能分析领域具有话语权。与其合作的“国家碰撞分析中心”(National Crash Analysis Center, NCAC)拥有世界上最准确的汽车碰撞试验资料库，其官方网站为研究人员免费提供可靠的汽车有限元模型。本文使用的汽车有限元模型即是NCAC提供的标准双轴卡车有限元模型。该车模型原重为7.17 t，笔者通过改变相关参数将汽车质量提高到8 t，以符合我国常见的双轴卡车重量，有限元模型如图1所示。

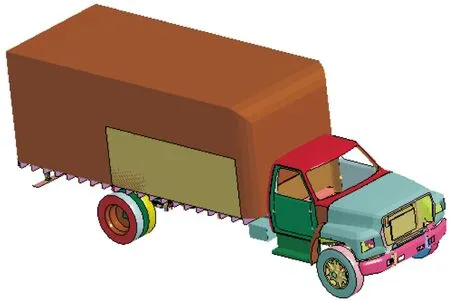
图1　汽车数值模型

1.2箱型梁桥数值模型

参考文献[7]建立了典型的预应力混凝土箱型梁桥上部结构数值模型。该桥梁由5个箱型梁组成，其中单个箱梁横截面尺寸及配筋图如图2所示。桥梁标准跨径为30 m，桥面宽度为15 m，可供四车道车辆同时行驶。桥梁边界条件采用板式橡胶支座，上部结构与支座定义为自动面面接触，摩擦系数为0.3[2]。

图2　箱梁横截面尺寸及配筋/mm

采用分离式建模，钢筋采用梁单元划分，混凝土采用六面体实体单元划分。钢筋和混凝土采用共节点处理，不考虑它们之间的粘结滑移效应[8]。其中，混凝土强度等级取为C50，单根箱梁预应力钢筋面积为7848 mm2，预应力值为1200 MPa。梁箍筋每隔100 mm配452 mm2的HRB300钢筋。其它配筋皆按照交通部专家委员会编制的《公路桥涵通用图》布置，并皆为二级钢筋，桥梁上部结构有限元模型如图3所示。

图3　单根箱梁有限元模型

1.3汽车-箱型梁桥耦合模型

本文运用后处理软件LS-PREPOST将汽车和预应力混凝土箱型梁桥的数值模型耦合在一起。计算中，汽车行驶速度取为80 km/h，汽车车厢与桥梁上部结构接触定义为面面接触。参考欧洲规范EUROCODE 1[1]的规定，本文将汽车超高值取为250 mm(车辆净高与桥下净空的差值)，其余设置皆按照文献[9]设置。汽车与预应力箱型梁桥的耦合模型如图4所示。

图4　汽车-桥梁上部结构的耦合模型

1.4材料选择

本文普通钢筋材料采用LS-DYNA中*MAT_PLASTIC_KINEMATIC(MAT3)[10]。钢筋材料模型的的屈服应力可以表示为

(1)

采用的普通钢筋材料参数如表1。

表1　钢筋材料参数

预应力钢筋材料采用LS-DYNA中*MAT_ELASTIC_PLASTIC_THERMAL(MAT4)[10]。利用此种材料“热胀冷缩”特性，当温度下降时，钢筋收缩，从而压缩混凝土，混凝土中产生预压应力。利用*LOAD_THERMAL_LOAD_CURVE关键字加载温度荷载。

混凝土材料采用*MAT_CONCRETE_DAMAGE_REAL3(MAT72)[10]。由于在冲击荷载作用下混凝土的抗压强度与静载作用时会有不同程度的提高，所以有必要考虑混凝土的应变率效应。混凝土材料应变率效应应根据CEB模型的建议，通常用材料强度动力增大系数DIF(Dynamic Increase Factor)来表示，DIF为在某一应变率下材料的动力强度与静力强度之比。

混凝土受拉时按以下公式计算强度增大系数TDIF：

(2)

混凝土受压时按以下公式计算强度增大系数CDIF：

(3)

2数值模型计算验证

图5　试验T梁模型

图6　试验有限元模型

图7　T梁有限元模型及配筋/mm

本文建立了文献[11]所做试验对应的有限元模型，其试验模型和有限元模型分别如图5和图6所示。该试验是以缩尺试验的方法，用罐体模型撞击钢筋混凝土T梁模型，以模拟现实中罐车撞击T型梁桥上部结构的情形。由图5可以看出，该试验采用的是反位试验。其中，罐体通过腹部若干点由缆绳约束，抬升至一定高度使之落下，获得的初速度为2.855 m/s，罐体与T梁的撞击区高度(罐体顶面到桥梁底面)为50 mm。在对应的有限元模型中，罐体采用壳单元来进行划分，其材料模型采用上文提到的*MAT_PLASTIC_KINEMATIC(MAT3)，支座采用实体单元自由划分，支座材料采用*MAT_RIGID(MAT20)[10]刚体材料，其它材料的选择与上文一致。采用精细化建模，建立了与试验模型一致的钢筋笼，钢筋单元和混凝土单元采用共节点，如图7所示，材料强度取值与试验一致。T梁与支座、钢筋混凝土梁接触皆采用自动面面接触，接触面间的摩擦系数取为0.5。将试验通过加速度积分算出的T梁受撞击部位最大点的位移时程与有限元模拟相应部位最大点位移时程结果对比，如图8所示。

图8　跨中位移时程比较

从图8可以看出，本文采用LS-DYNA建立的数值模型计算结果与试验测试结果吻合较好。无论T梁顶面还是底面，最大位移值相差不大，位移发展基本趋势大体相似。因此，可以断定，用有限元软件LS-DYNA以及采用上文提到的模型建立和材料参数设置来进行模拟超高车辆撞击桥梁上部结构动态响应分析是真实可靠的。

3不同撞击位置的桥梁损伤对比

3.1数值分析初始条件

本文将计算过程分为两个阶段，第一阶段为初应力加载阶段，第二阶段为车-桥碰撞阶段。

在第一阶段中，为减少计算单元，只建立桥梁上部结构模型，对桥梁上部结构施加重力、桥面上部荷载以及预应力荷载。为了让结构能够快速稳定下来，通过试算，估计出结构临界阻尼，加到桥梁模型上。在施加重力荷载时，分两步加载：荷载首先由零开始线性增加至重力加速度大小，加载时长为0.5 s，待桥梁上部结构稳定之后，保持荷载不变，直到第二阶段碰撞结束。

本文利用了LS-DYNA的重启动功能，在第二阶段中撤掉结构上的阻尼，避免阻尼对碰撞结果产生影响。同时，加入车辆模型，给予车辆80 km/h的初速度，分别撞击桥梁跨中处，距桥梁端部10 m处，距桥梁端部5 m处，本文分别称为工况一、工况二、工况三，如图9所示。

图9　三种工况

3.2不同撞击位置桥梁损伤对比

图10是三种工况下模型计算至1.2 s时的桥梁损伤图，可以看出，桥梁的局部损伤主要是在桥梁底部和箱梁被撞面另一侧。其中，底部混凝土大面积脱落、钢筋屈服，这是因为车厢变形后对箱梁底的冲切所致。而箱梁另一侧的混凝土脱落是因为箱梁受冲击使得另一面混凝土局部受压破坏。通过对比三种工况下桥梁损伤情况可以发现，工况三混凝土脱落面积最大，工况二次之，工况一最小，说明超高车辆撞击桥梁的位置不同，对桥梁造成的损伤也会不同。撞击位置离支座距离越近，桥梁受到的破坏就越大，原因是离支座越近，桥梁受到支座的约束越强，刚度相对就越大，使得撞击更为猛烈。

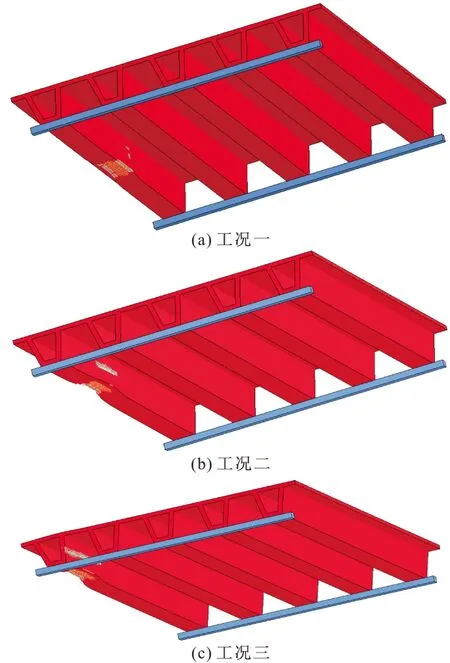
图10　三种工况下桥梁的损伤

3.3不同撞击位置下点位移及撞击力对比

在被撞箱梁另一侧取三个碰撞区域关联点，分别命名为点A、B和C，如图11所示。其中，A点为工况一箱梁被撞区域对应另一侧跨中一点，其距离箱梁底面高度为250 mm，距离梁端距离为15 m；B点为为工况二箱梁被撞区域对应另一侧跨中一点，其距离箱梁底面高度为250 mm，距离较近梁端为10 m；C点为为工况三箱梁被撞区域对应另一侧跨中一点，其距离箱梁底面高度为250 mm，距离较近梁端为5 m。图12是三种工况下，三个点的X方向位移时程曲线图，可以看出，三种工况各自在其撞击区域对应的那一点位移较大，其它两点位移较小。而且，工况三对应点的最大位移﹥工况二对应点最大位移﹥工况一的对应点最大位移。产生这种现象的原因是由于碰撞区域离端部越近，桥梁受到端部支座的约束越强，使得碰撞更为猛烈，致使局部损伤更为严重，表现为位移越大。另外，通过图12可以看出，工况一和工况二对应的最大位移时程曲线出现了反弯的现象，工况三没有反弯现象，而且随着撞击位置离端部越近，反弯现象越不明显，原因是因为碰撞区域离端部越远，受端部支座的约束越弱，使得刚度相对较弱，相对“柔一点”，因此会有反弯现象。图13给出了三种工况下碰撞力的时程对比，可以看出三种工况的碰撞力峰值由大到小依次为为工况三、工况二、工况一。这进一步的验证了上文提到的，撞击区域离端部越近，撞击更为猛烈。

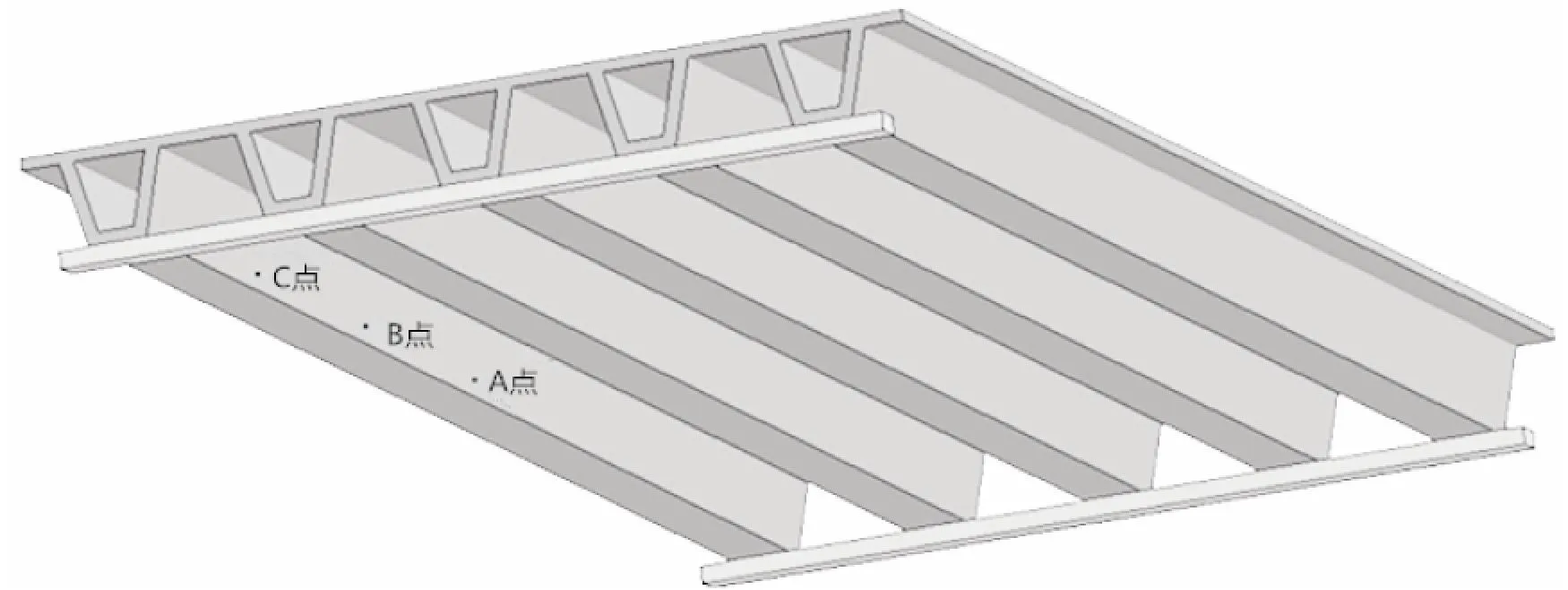
图11　数据采集点

图12　不同工况下三点位移时程曲线

图13　不同工况下碰撞力时程曲线

3.4撞击过程的能量转化

使用有限元单点积分方法可以大幅度降低计算成本，但关键要看能不能控制沙漏能的大小。因此，查看沙漏能(Hourglass Energy)与总能量(Total Energy)随时间变化的数值，判断其能量变化是否合理，显得非常必要。由于三种工况数值模拟方法一致，故单独拿出工况一的能量变化进行分析，如图14所示。该图显示了车桥碰撞过程中各种能量之间的动态变化走向。由此图可以看出，总能量基本保持不变，90%以上的动能转化为了内能，沙漏能占总能量的比例不到10%。因此，可以断定这次碰撞过程能量变化是合理的，也证明了这次数值模拟的正确性。

图14　能量变化

4结论

(1)根据相应试验建立的有限元模型数值分析结果与试验结果对比发现：利用LS-DYNA软件进行超高车辆撞击桥梁上部结构的模拟分析方法是可信的。

(2)不同撞击位置下，超高车辆以80 km/h的速度撞击预应力箱梁上部结构可以造成桥梁底部混凝土大面积脱落、钢筋屈服，箱梁被撞区域对应另一侧混凝土局部受压破坏，混凝土脱落。

(3)撞击位置越是靠近桥梁端部，车桥碰撞产生的碰撞力越大，局部损伤也就越大，表现为局部位移较大，局部混凝土脱落面积较大。因此，超高车辆撞击预应力箱梁考虑最不利情况应研究车辆撞击桥梁支座处的破坏情况。

[1]EN 1991-1-4-2005, EUROCODE 1: Actions on Structures[S].

[2]JTG D60-2004, 公路桥涵设计通用规范[S].

[3]毕晨华, 张永水. 超高车辆碰撞桥梁的有限元损伤分析[J]. 重庆交通大学学报(自然科学版), 2011, 30(6)： 1294-1297．

[4]陆新征, 张炎圣, 叶列平, 等. 超高车辆-桥梁上部结构碰撞的破坏模式与荷载计算[J]. 中国公路学报, 2009, 22(5)： 60-67.

[5]陆新征, 张炎圣, 宁静, 等. 超高车辆与立交桥梁碰撞的高精度非线性有限元仿真[J].石家庄铁道学院学报, 2007, 20(1)： 29-34.

[6]陆新征,何水涛,黄盛楠. 超高车辆撞击桥梁上部结构研究——破坏机理、设计方法和防护研究[M]. 北京：中国建筑工业出版社, 2011.

[7]闫志刚.钢筋混凝土及预应力混凝土简支梁桥结构设计[M]. 北京：机械工业出版社, 2009.

[8]Krauthammer T, Shahriar S, Shanaa H M. Response of reinforced concrete element severe impulsive loads[J]. Journal of Structural Engineering New York N Y, 1990, 116(4): 1061-1079.

[9]赵海鸥. LS-DYNA动力分析指南[M]. 北京: 兵器工业出版社, 2003.

[10]LS-DYNA. Keyword User’s Manual[Z]. Livermore, California：Livermore Software Technology Cooporation, 2006．

[11]何水涛, 陆新征, 卢 啸, 等. 超高车辆撞击钢筋混凝土T梁桥主梁试验研究[J]. 兰州交通大学学报, 2011, 30(6): 20-25.

Dynamic Response of the Pre-stressed Box Girder Bridge to

Over-high Truck Impact Under Different Impact Position

TIANLi,FENGZhen-ning

(School of Civil Engineering, Tianjin University, Tianjin 300072, China)

Abstract:With the acceleration of the urbanization, the accidents of the over-high truck impacting the pre-stressed box girder bridge superstructure have occurred. Therefore, it is necessary to study the dynamic response of this kind of the impact. A three-dimensional separation model of the fine T bridge superstructure is established by LS-DYNA, and the collision analysis of tank and the T bridge is made. The accuracy of the LS-DYNA simulation was verified by comparison with the experiments. The three-dimensional separation model of the fine pre-stressed box girder bridge superstructure is established by LS-DYNA, and the coupling models of the vehicle and bridge superstructure under three working conditions are established respectively. Through the calculation results can be seen in the bridge damage location and condition are roughly similar. The more close the impact position to the bearing, the more serious damage to the bridge. The results show that the more close the impact position to the bearing, the greater the impact force and the greater the displacement of the impact area. It can be Concluded that the impact of the high vehicle impact on the pre-stressed concrete box girder, the most unfavorable situation should be considered to study the failure of the vehicle impact bridge bearing.

Key words：box girder bridge; vehicle impact; discrete model; dynamic response

中图分类号：U447; U441+.3

文献标识码：A

文章编号：2095-0985(2016)01-0018-06

基金项目：国家自然科学基金 (51178310；50678116)

作者简介：田力(1970-)，男，天津人，副教授，博士，研究方向为工程结构抗爆、抗冲击理论(Email:ltian@tju.edu.cn)

收稿日期：2015-08-03修回日期： 2015-10-29