基于匹配滤波的伪码信号捕获搜索间隔优化与分析

赵鑫,黄新明,李井源,朱祥维,孙广富

(国防科技大学 电子科学与工程学院 卫星导航定位技术工程研究中心,长沙 410073)

基于匹配滤波的伪码信号捕获搜索间隔优化与分析

赵鑫,黄新明,李井源,朱祥维,孙广富

(国防科技大学 电子科学与工程学院 卫星导航定位技术工程研究中心,长沙 410073)

传统伪码信号检测方法优化分析仅仅从检测能力角度优化多普勒频率和码相位搜索间隔,没有考虑复杂度的影响。单位复杂度等效理想检测因子融合检测信噪比和捕获过程的复杂度,更全面更贴近实际体现频率和码相位间隔的影响。本文利用单位复杂度等效理想检测因子对频率搜索间隔和码相位搜索间隔联合优化,通过对单位复杂度等效理想检测因子进行求导,推导出频率和码相位搜索间隔优化值公式。通过仿真,改进的单位复杂度等效理想检测因子联合优化方法理论与实际仿真结果较吻合,而且对已有的相对等效理想检测因子单独优化方法进行仿真对比,基于单位复杂度等效理想检测因子联合优化方法得到的频率和码相位间隔检测能力较强,并且对不同相干积分条件进行优化仿真,总结优化值变化规律,为接收机设计提供指导。

捕获性能优化;单位复杂度等效检测能力因子;联合优化;频率搜索间隔;码相位搜索间隔

0 引 言

随着卫星导航系统的发展,导航接收机的研究无时无刻不在更新。作为经典的捕获算法,匹配滤波捕获算法已经非常成熟[1-2],常用的主要有并行频率搜索[3]和并行码相位搜索捕获[4],用途十分广泛。但是对于匹配滤波捕获算法频率和码相位搜索间隔的研究并不常见,频率和码相位搜索间隔的选取关系到相干积分过程的损耗,影响检波输入信噪比,直接对捕获性能造成影响。就目前来看,BPSK信号频率和码相位搜索间隔一般采用500 Hz和0.5个码片经验值,但是并不知晓其中原因,而且面对不同的自相关函数,不同的相干积分时间,并没有通用的方法来指导和优选频率和码相位搜索间隔,故频率和码相位搜索间隔选取的研究显得十分重要。

匹配滤波算法在雷达领域应用广泛,其中文献[5]中提出单位复杂度的概念,并用此来衡量相关部分的复杂度,文献[6]给出了理想检测能力因子的概念以衡量检测性能。文献[7]结合两个概念中提出了单位复杂度等效理想检测因子,并从此出发对频率和码相位搜索间隔进行了优化。本文以此为基础,从基于平方检波匹配滤波算法出发,进一步研究单位复杂度等效理想检测因子优化频率和码相位间隔,给出不同条件下优化频率和码相位搜索间隔结果和理论推导,匹配滤波器结构如图1所示。

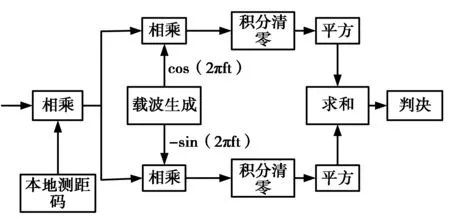
图1 匹配滤波器

本文重点研究单位复杂度等效理想检测因子联合优化频率和码相位搜索间隔。第二部分介绍单位复杂度等效理想检测因子概念和已有的优化方法;第三部分给出本文改进的联合优化方法,第四部分呈现不同条件下的仿真,并对比本文方法与已有方法的捕获性能;最后,对文章的方法进行总结。

1 单位复杂度等效理想检测因子

1) 复杂度

假设信号的码率为n×1.023 Mcps,则基带信号两路信号相干运算的计算复杂度为相干过程的单位复杂度Ocorr,搜索过程复杂度为Os,搜索层复杂度是建立在相关部分基础上的,于是搜索过程复杂度[5]计算如下:

(1)

假设搜索过程单位复杂度为Osu,其码片搜索间隔为τum个码片,频率搜索间隔为fmnHz,于此,可以得到搜索过程复杂度与搜索过程单位复杂度关系

(2)

式中,τunc,func分别为码相位和频率不确定范围,τbinfbin分别是码相位和频率搜索间隔,τunifum可取任意值,方便计算即可。

2) 等效理想检测因子

理想检测因子[6]是指在相干条件下,达到要求的检测性能所需的信噪比,而等效理想检测因子是指在捕获的过程中,为达到指定的性能,所对应理想检测因子。针对基于平方检波的匹配滤波器,其等效检测因子[8]为

(3)

其中,SNR为输入检波信噪比,其表达式为

(4)

式中:C/N0为载噪比;Tc为相干积分时间;fd为多普勒频率;R(τ)为基带信号自相关函数;τ为码相位。

由于多普勒频率,码相位偏差等因素,输入检波信噪比与理想信噪比相比存在损耗,常见的三种损耗为

(5)

其中:Lfilter为匹配滤波器损耗,一般在无限带宽下其为1,有限带宽下略大于1;Lcode为相位偏差引起的损耗,Lfreq为频率偏差引起的损耗。

一般来说,上述的三种损耗之间是相互独立的,因此可以单独考虑其中一种引起的误差,以最小值原则获得频率搜索间隔和相位搜索间隔优化值。

3) 单位复杂度等效理想检测因子

假设不考虑非相干积分,相关部分的等效理想检测因子为D,搜索过程的复杂度为Os,则单位计算复杂度等效理想检测因子[7]为

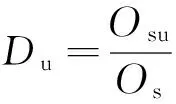
(6)

考虑到损耗之间的独立性,已有的优化方法对上式进行简化,采用相对单位复杂度等效理想检测因子最大值原则优化频率和码相位搜索间隔,其表达式为

(7)

(8)

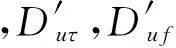
联系实际搜索过程,相位偏差和频率偏差是未知的而且是随机的,于是采用最恶劣条件下的最大损耗Lcodemax,Lfreqmax带入相对单位复杂度等效理想检测因子中来获取优化间隔,最大损耗获取表达式为

(9)

(10)

2 伪码捕获二维联合优化方法

已有的频率与码相位搜索间隔的优化存在一定的局限性:

1) 相对单位复杂度等效理想检测因子是对单位复杂度等效理想检测因子的简化,不能全面体现频率与码相位搜索间隔对捕获的影响。

2) 已有优化过程对频率和码相位搜索间隔优化是相互独立的,而且没有得到最终推导公式。实际上频率和码相位搜索间隔两者共同作用输入检波信号的信噪比,影响最后的检测性能(理想检测因子)。

因此,本文拟采用单位复杂度等效理想检测因子对频率和码相位搜索间隔进行二维联合的优化,使之接近实际使用情况,并且对其进行理论推导,求出理论优化值表达式。

将式(2)、式(4)、式(8)、式(9)带入单位复杂度等效理想检测因子式(6)中,其中假设R(0)=1,考虑频率偏差和码相位带来的最大损耗,得到:

(11)

优化τbin,fbin,采用单位复杂度等效理想检测因子最大原则,通过求导数来获得优化值表达式:

(12)

令m=C/N0×Tc,R(τ)=-τ+1,

v=τunifuni×

对于码相位搜索间隔求导公式,有:

(13)

进一步可得:

(14)

对于频率搜索间隔求导等式:

(15)

其中:

将上式带入式(15)后

(16)

结合式(14),式(16)可以得到:

(17)

为码相位搜索间隔与频率搜索间隔之间的关系

将码相位搜索间隔推导公式带入频率搜索间隔推导公式(14)可以得到:

(18)

此推导优化公式较为复杂,求解可以通过数值计算的方法,求出符合要求的结果。下面对该结果进行仿真验证。

3 数值计算和优化对比

1) 优化方法性能对比

为了体现本文方法的优势,自相关函数和相干积分时间均采用BPSK信号常用的数值(相干积分常用1ms),利用已有的相对单位复杂度等效理想检测因子单独优化和本文提出的基于单位复杂度等效理想检测因子二维联合优化方法寻找频率和码相位搜索间隔优化值,并对其捕获性能进行比较。优化实验条件为

Tc=1 ms,K=1,CN0dB=40 dBHz,

R(τ)=-|τ|+1，|τ|<=1.

① 相对单位复杂度等效理想检测因子单独优化

采用已有的基于相对单位复杂度等效理想检测因子单独优化码相位搜索间隔和频率搜索间隔,优化结果如图2、图3所示。

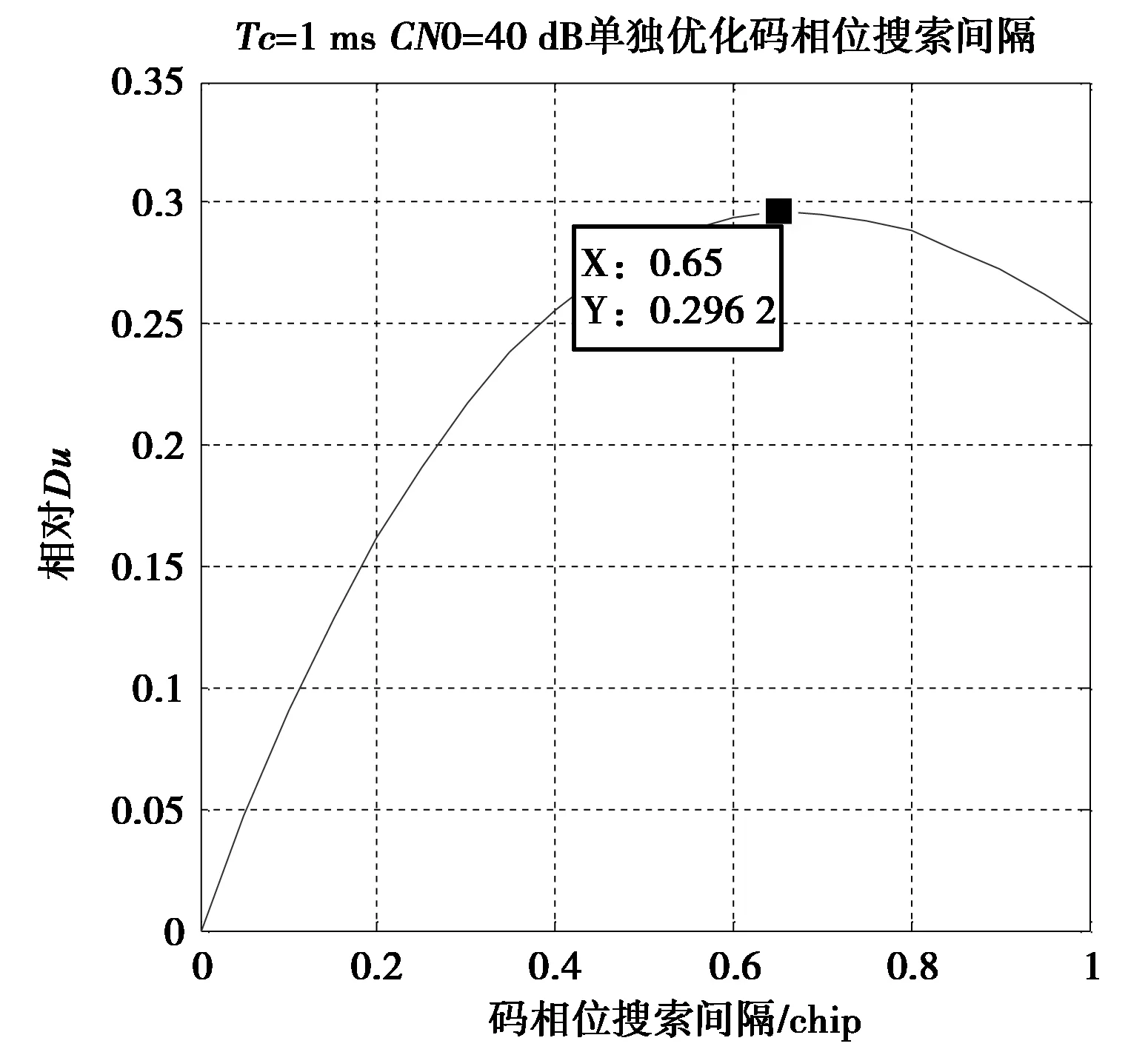
图2 相对Du与码相位的关系

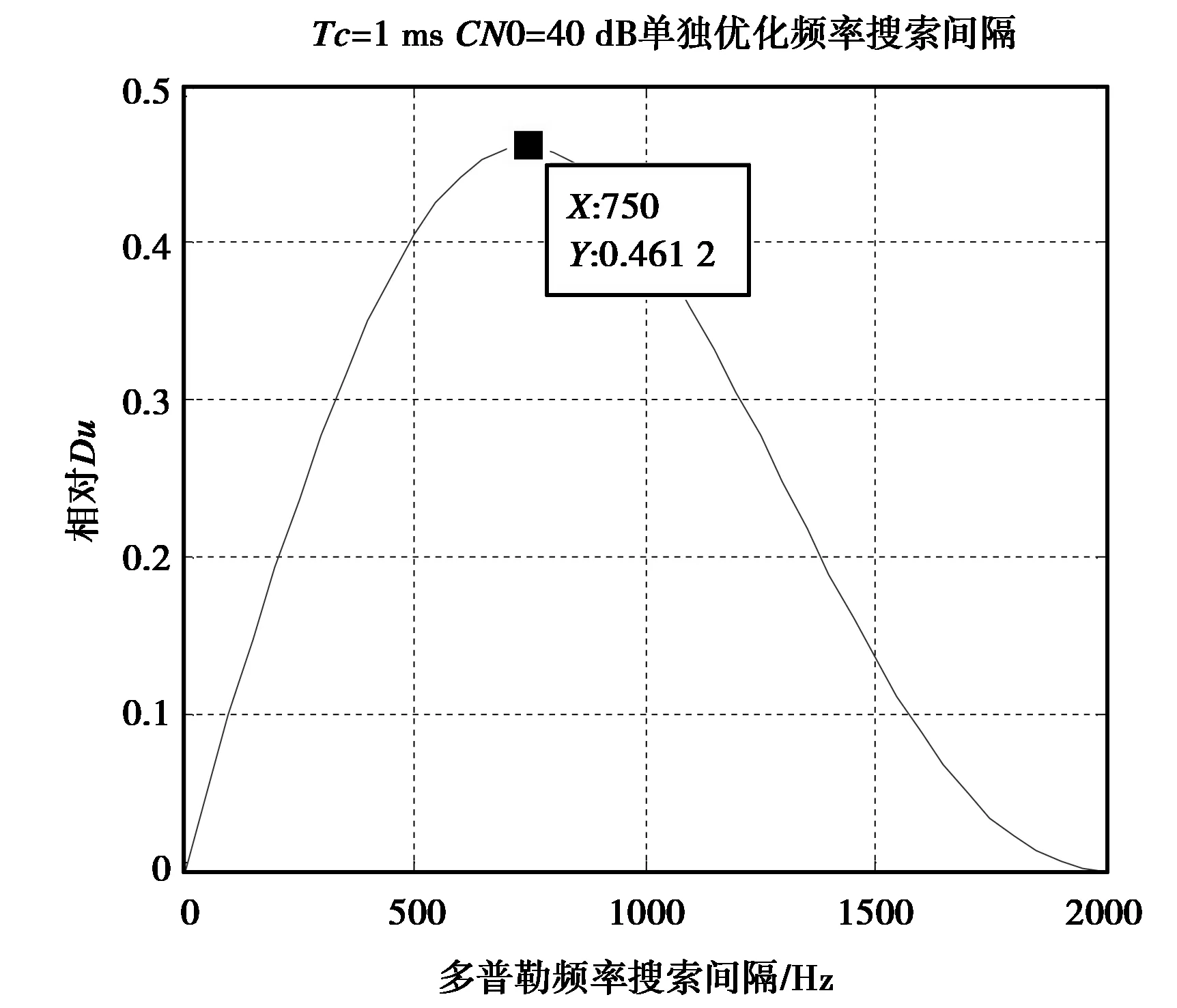
图3 相对Du与频率间隔的关系

② 单位复杂度等效理想检测因子二维联合优化

基于单位复杂度等效理想检测因子二维联合优化频率和码相位搜索间隔,实质上是以单位复杂度等效理想检测因子最大原则在一定的范围内寻找频率和码相位搜索间隔,其优化结果如图4所示。

为了验证本文基于单位复杂度等效理想检测因子推导的频率和码相位间隔优化值公式,在此采用理论数值计算方法求解频率和码相位间隔优化值。

令x=Tc×Fbin/2,求解公式(18),如图5和图6所示。

由图可知:x=0.320 8,fbin=0.320 8×2/1e-3=642 Hz,带入式(17)可得:τbin=0.534,综合以上仿真,可以得到表1所示的结果。

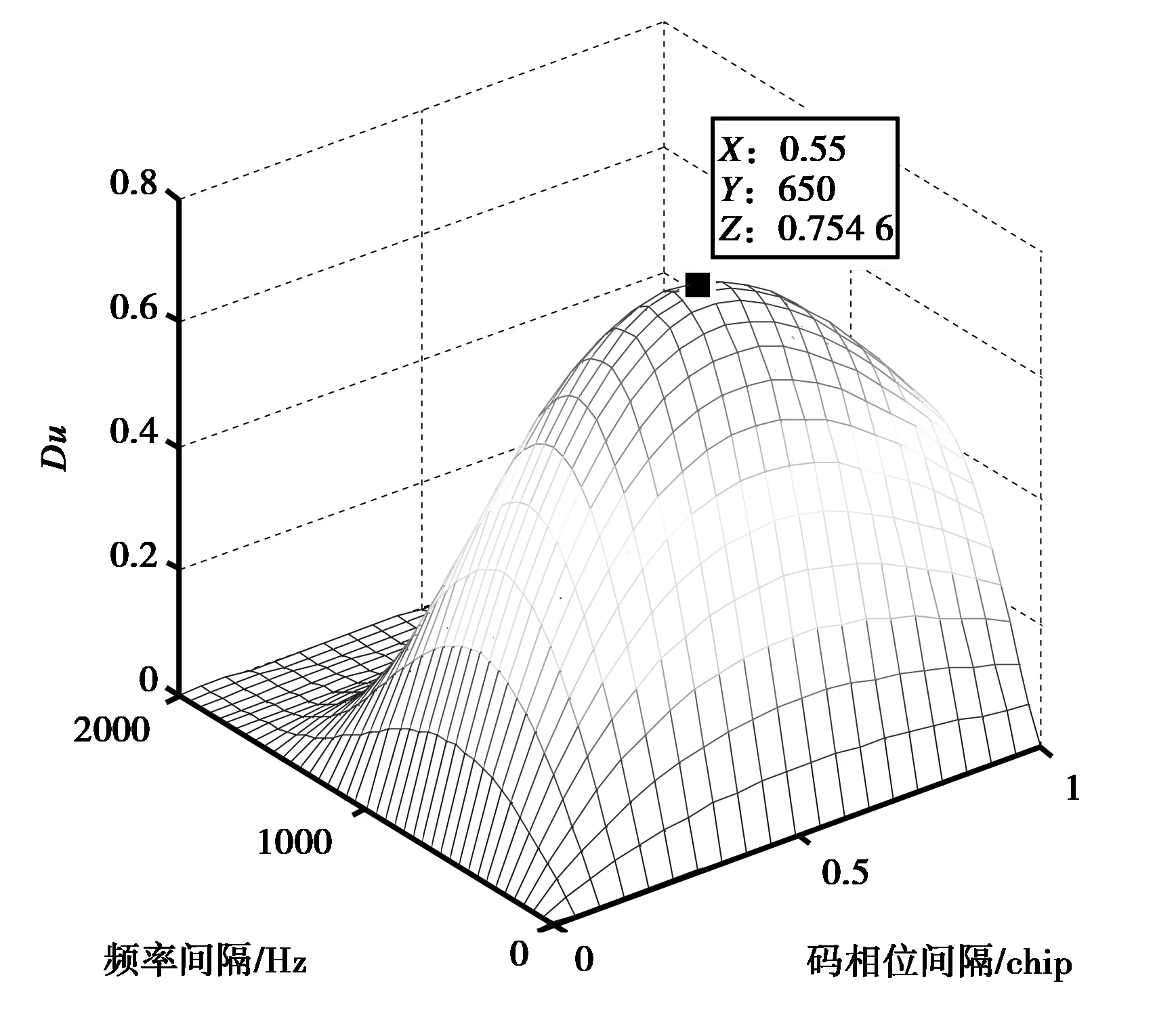
图4 基于Du二维联合优化方法优化图

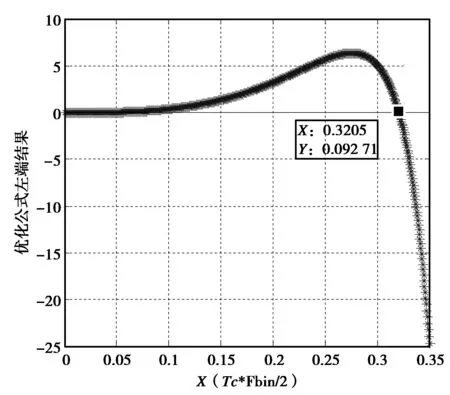
图5 数值求解曲线

图6 数值求解曲线局部放大图

表1 两种方法优化结果及性能比较(理想输入检波信噪比SNR0=10)

由表1可知,传统的相对单位复杂度等效理想检测因子独立优化获取的搜索间隔与本文提出的改进方法差距较大,最终检波输出的信噪比远远低于联合优化结果对应的输出信噪比,使得最终的捕获性能比本文的优化方法差。显然,本文提出的基于单位复杂度等效理想检测因子联合优化方法更贴近实际,优化的搜索间隔可以获得更优的检波输出信噪比,提高检测能力,为接收机设计提供指导。而且通过理论优化公式计算的结果与直接采用基于单位复杂度等效理想检测因子曲线优化的结果一致,验证理论推导的正确性,下面的优化均采用曲线优化,不再进行计算。

2) 不同相干积分时间条件的二维优化对比

此部分主要采用单位复杂度等效理想检测因子寻找频率和码相位搜索间隔二维优化,主要分为以下三个仿真情景。中频积累时间Tc分别为5 ms、1 ms、2 ms和0.5 ms.通过优化,可以得到表2所示的结果。

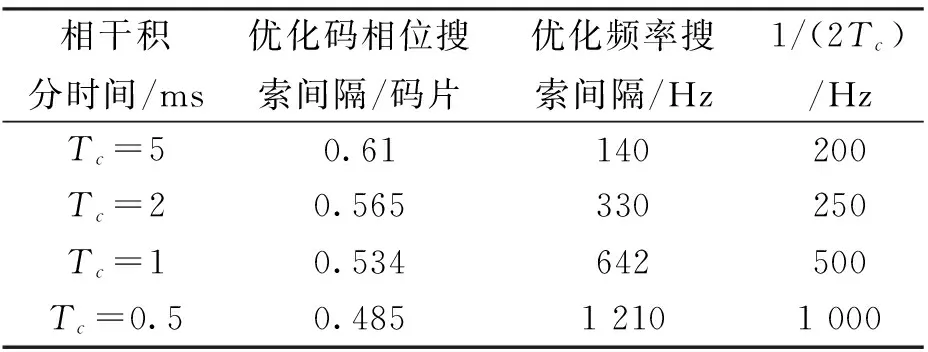
表2 不同相干积分条件下优化结果比较

由表2可知,随着相干积分时间的提高,采用二维联合优化方法,码相位搜索间隔缓慢提高,基本上在0.5个码片左右,频率搜索优化间隔不断减小，可根据相干积分数值选择优化搜索间隔。

3) 不同载噪比条件下的二维优化对比

此部分采用基于单位复杂度等效理想检测因子二维优化方法寻找频率和码相位搜索间隔,仿真条件与式(1)基本相同,其中载噪比CN0分别为36、38、40、42、44 dB.通过优化和理论计算,结果如表3所示。

由表3可知,随着载噪比的不断提高,优化的码相位和频率搜索间隔缓慢变大,码相位间隔优化值在0.5码片左右,频率搜索间隔在600 Hz左右,说明载噪比的变化对本文的二维联合优化方法影响较小,但是不可忽略,在实际的工程中需要根据信号的载噪比来选择优化频率间隔，码片相位间隔。

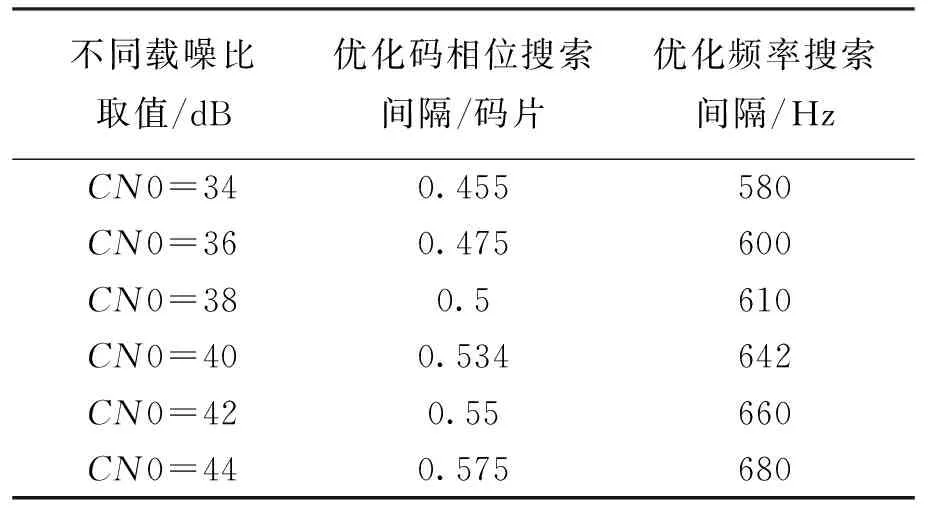
表3 不同载噪比调价下优化结果对比

4 结束语

本文旨在寻找匹配滤波捕获算法中优化频率和码相位搜索间隔的通用方法,在相对单位复杂度等效理想检测因子单独优化搜索间隔方法的基础上,提出利用单位复杂度等效理想检测因子进行二维联合优化方法,理论推导出一定条件下的频率和码相位搜索间隔优化公式,并对此作优化和理论计算,得出以下结论:

1) 基于单位复杂度等效理想检测因子二维联合优化方法获得的频率和码相位搜索间隔与相对单位复杂度等效理想检测因子单独优化的结果差距较大,而且二维优化的结果对应的检波输出信噪比高于单独优化结果对应的信噪比,捕获能力得到提升,本文提出的二维联合优化的方法效果更好。

2) 通过优化对比可知,相干积分时间对频率搜索优化间隔影响较大,对码相位优化搜索间隔影响较小,而载噪比对码相位和频率搜索间隔均影响较小。工程中可按照本方法选取对应的优化间隔,同时通过BPSK优化可以很好地解释通常选择采用0.5码片和500 Hz频率搜索优化间隔的理由,对于其他的捕获算法也可以参照本方法来需找频率和码相位搜索间隔优化值,为接收机设计提供指导。

[1] 谢钢.GPS原理与接收机设计[M].北京:电子工业出版社,2009.

[2] 朱祥维,王飞雪,基于平方律检波的二相编码信号分段相关——视频积累方法研究[J].电子学报,2005(3):545-548.

[3] ZHENG Y Z, ZHANG Y X. An improved segmented match filters with FFT approachfor GNSS signal acquisition[C]// 2010 2nd International Conference on Computer Technology and Development, 2010:425-428.

[4] QIU L, LI L, GPS signal acquisition based on FFT[C]// 2010 2nd International Conference on Computer Technology and Development,2010:110-113.

[5] DAFESH P A, HOLMES J K. Practical and theoretical tradeoffs of active parallel correlator and passive matched filter acquisition implementations[C]//Proceedings of the IAIN World Congress and the 56th Annual Meeting of the Institute of Navigation,2000:352-367.

[6] BARTON D K. Simple procedures for radar detection calculations[J]. IEEE Transactions on Aerospace and Electronic Systems,1969,5(5):837-846.

[7] 刘瀛祥,现代化导航信号高精度建模与接收技术研究[D].长沙:国防科学技术大学,2014.

[8] BARTON D K. Modern radar system analysis[M]. Norwood, MA: Artech House Inc.,1988.

Optimization and Analysis of Pseudorandom Code Signal Acquisition Search Interval Based on Matched Filter

ZHAO Xin,HUANG Xinming,LI Jingyuan,ZHU Xiangwei,SUN Guangfu

(CollegeofElectronicScienceandEngineering,NationalUniversityofDefenseTechnology,Changsha410073,China)

Optimization and analysis of the traditional Pseudo-code signal acquisition search interval method only optimizes the Doppler frequency and the code phase search interval from the viewpoint of detection capability, without considering the influence of complexity. The the ideal detection factor of unit complexity combines detection signal to noise ratio and complexity of the acquisition, more comprehensive and closer to the actual influence of the frequency and code phase interval. In this paper, I use the equivalent ideal detection factor of unit complexity to optimize the frequency search interval and the code phase search interval, and derive the optimal formula of frequency and code phase search interval by deriving the equivalent ideal detection factor of unit complexity. The simulation results show that the proposed method is better and more effective than the relative equivalent ideal detection method. Based on the equivalent ideal detection factor of unit complexity joint optimization, this paper acquires the optimization of frequency and code phase search interval by the simulation of different coherent integration conditions, and summarizes the variation rule of optimal value, and provides guidance for receiver design.

Acquisition; equivalent detection capability factor of unit complexity(Du); joint optimization; frequency search interval; code phase search interval

2016-09-10

10.13442/j.gnss.1008-9268.2016.06.009

P228.4

1008-9268(2016)06-0042-06

赵鑫(1992-),男,安徽蒙城人,硕士生,主要研究方向为卫星导航信号体制和接收机技术。

黄新明(1988-),男,湖北武汉人,讲师,主要研究方向为卫星导航系统时间同步和信号处理。

李井源(1982-),男,山西太原人,讲师,主要研究方向为卫星导航系统信号体制、接收机信号处理、站间视频传递等。

朱祥维(1980-),男,山东日照人,副研究员,研究生导师,主要研究方向为卫星导航系统、体制设计、全数字接收机、高精度测量。

孙广富(1970-),男,黑龙江巴彦人,研究员,博士生导师,主要研究方向为卫星导航信号接收技术。

联系人：黄新明 E-mail: huangxinming@nudt.edu.cn