侧向变位对板桩墙土压力影响的研究综述

陈 达，汪 啸，杨一琛，2，邓永锋

（1.河海大学港口海岸与近海工程学院，南京210098；2.中交上海航道勘察设计研究院有限公司，上海200120；3.东南大学交通学院岩土工程研究所，南京210096）

侧向变位对板桩墙土压力影响的研究综述

陈 达1，汪 啸1，杨一琛1，2，邓永锋3

（1.河海大学港口海岸与近海工程学院，南京210098；2.中交上海航道勘察设计研究院有限公司，上海200120；3.东南大学交通学院岩土工程研究所，南京210096）

板桩码头具有结构简单、施工方便、对复杂的地质条件适应性强等诸多优点，被广泛应用于沿海和内陆地区。常规的设计方法假定作用在板桩墙前后的土压力达到主动与被动极限状态，然而在板桩墙的施工和使用过程中，由于受到土体与锚碇结构的共同作用，整个墙体的侧向变形和位移会受到不同程度的限制，所以实际的土压力并不处于极限状态，这可能导致工程设计过于保守而造成浪费或过于轻率而产生安全隐患。因此，众多学者围绕侧向变位对板桩墙前后土压力的影响开展了卓有成效的研究。文中对土体侧向变形对土压力系数的影响和板桩墙变位对土压力的影响进行了综述和归纳，明确了板桩墙所受土压力的变化规律，并探讨了后续需进一步研究的问题。

板桩墙；变形；位移；土压力系数；土压力

我国建国以来，码头建设技术有了很大发展，多种码头结构形式相比之下，板桩码头方面的进展相对较慢。多年来我国主要将板桩结构形式用于中小型码头的建设，而国外的情况却大不相同，日本大部分码头采用钢板桩结构，他们认为板桩结构比其他结构型式便宜且施工简单；欧洲的应用更为普遍，几乎所有的码头都采用板桩结构。我国经过了60年的建港历史，目前水深、地基条件好的港址已经所剩无几了，现在正面临大量在滩涂、浅滩、粉砂质海岸和淤泥质海岸建港的形势，可以预言，今后板桩码头在我国的应用会越来越广。

目前在常规的设计中板桩墙受到的土压力一般取极限状态下的主、被动土压力，然而实际工程中由于板桩墙受到土体的嵌固作用和锚碇结构的支撑作用，结构位移受到限制，作用在墙后的实际土压力并不处于极限状态，实际的土压力是板桩与土相互作用的结果［1］。根据国内外研究成果，板桩墙的变形方式主要有两类：一种是以转动（或整体水平）位移为主，如先挖泥后打桩、板桩相对刚度较大、锚杆位移较大等情况；另一种是以弯曲变形为主，如先打桩后开挖、板桩相对刚度较小，锚固点位移小等情况［2］。土与墙相互作用的复杂性，给板桩墙所受土压力的确定带来很大的困难，进而可能导致工程设计过于保守而造成不必要的浪费，或是过于轻率而带来严重的安全隐患。因此，研究板桩墙土压力的实际分布情况，给出合理的简化计算方法，对于码头设计的安全性与经济性是十分必要的。很多学者对此开展了大量研究，取得了丰富的成果。本文将从土体侧向变形对土压力系数的影响出发，进一步总结板桩墙变位对墙后土压力分布的影响规律，阐述需要进一步研究的内容，为板桩码头的建设和科研提供借鉴和指导。

1 土体侧向变形对土压力系数的影响

随着土体侧向变形的增大，板桩墙所受土压力逐渐从静止状态过渡到主动或被动状态，即土体的侧压力系数逐渐从静止土压力系数K0变为主动土压力系数Ka或被动土压力系数Kp。目前国内外许多学者对此进行了大量研究，以下将详细阐述关于静止土压力系数K0，主、被动土压力系数Ka、Kp以及中间状态土压力系数的研究成果。

1.1 静止土压力系数K0

静止土压力系数K0是岩土工程的基本参数之一，这一概念首先由Donath提出，当时被定义为土体在没有侧向变形的条件下由竖向荷载引起的水平向应力与竖直向应力的比值，即

在现代土力学理论中，K0被定义为半无限土体中一点的水平与竖直有效自重应力之比。为了满足工程应用的需要，许多学者研究了K0的经验公式以及室内或原位测量方法。

1.1.1 经验公式

（1）正常固结土K0的理论与经验公式

大多数学者均将K0表示为土体有效内摩擦角的函数，其中最为经典的是Jaky公式

之后Brooker和Ireland［3］对该式进行了修正，他们认为Jaky公式更适用于估算无黏性土的K0，并提出了适用于黏性土的公式

除了以上两式以外，Fraser［4］、Burland和Roscoe［5］、Matsuoka［6］、史宏彦［7］、强跃［8］等也以有效内摩擦角为参数，分别给出了不同形式的K0计算公式，可见采用有效内摩擦角对K0值进行估算已经被广泛认可了。然而这里存在着一个有问题的理论假设，有效内摩擦角代表土体的极限或是破坏应力状态，而K0所处的土体状态显然远未达到极限状态，故用有效内摩擦角来计算K0在理论上是不合适的。基于以上考虑，有学者就提出采用已激发内摩擦角φ'mob来代替有效内摩擦角φ'估算K0。

已激发内摩擦角φ'mob的概念最早由Terzaghi提出。在一维压缩固结过程中，水平与竖直有效应力的比值随竖向荷载的增加保持为常数，若将竖向加荷过程中土体的应力状态绘制成一系列莫尔应力圆，可以发现它们与同一条直线相切，如图1所示，这条公切线的倾角即为φ'mob，显然φ'mob＜φ'。

图1 极限状态及一维压缩状态莫尔应力圆Fig.1 Mohr circles of stress for soils at failure and under one-dimensional loading conditions

根据图1中莫尔应力圆与公切线的几何关系，Taylor［9］得出了用已激发内摩擦角φ'mob计算K0的理论公式

虽然φ'mob不能直接通过试验量测，但它与φ'存在一定的关联，许多学者对此进行了研究，现将他们的成果以及与历史文献中试验数据的相关程度归纳于表1。

除了有效内摩擦角φ'和已激发内摩擦角之外，也有学者提出采用其他参数计算K0。

Kenney［13］对历史文献中的数据进行处理，得出了K0与塑性指数Ip的一个尝试性的表达式

Alpan［14］认为：当假设土体为理想弹性材料时，K0与土体泊松比存在式（6）所示的关系。

（2）考虑应力历史的K0计算公式

Brooker和Ireland［3］对5种黏性土的重塑样进行一维压缩试验，发现K0随超固结比OCR的增大而增大，最终趋近于被动土压力系数Kp。Alpan［14］对Wiseman和Brooker［3］的试验数据归纳得到下式

当使用对象为砂土时，λ与内摩擦角有关，且随着内摩擦角的增大而减小；当使用对象为黏土时，λ与塑性指数有关，且随着塑性指数的增大而减小。

Hanna［15］通过室内模型试验来验证Wroth、Meyerhof［16］、Mayne和Kulhawy［17］提出的K0受OCR影响的经验公式（见表2），结果表明当OCR≤3时，各公式计算结果均与试验数据吻合良好；Hanna同时给出了与任意OCR值对应的K0试验值吻合良好的经验公式。

1.1.2 试验测量

测量K0的试验一般分为室内单元试验与原位试验。

室内单元试验常利用固结仪或三轴仪进行。固结仪限制了试样的侧向变形，只要在试样压缩固结过程中测得其轴向压力和侧向压力，就能根据σh～σv关系，利用式（1）求得K0值。三轴仪没有限制试样的侧向变形，因此在施加轴向压力的同时需要同步增加侧向压力来保证试样不产生侧向变形，根据测得的轴向压力、侧向压力和孔隙水压力，利用有效强度指标来计算K0值。

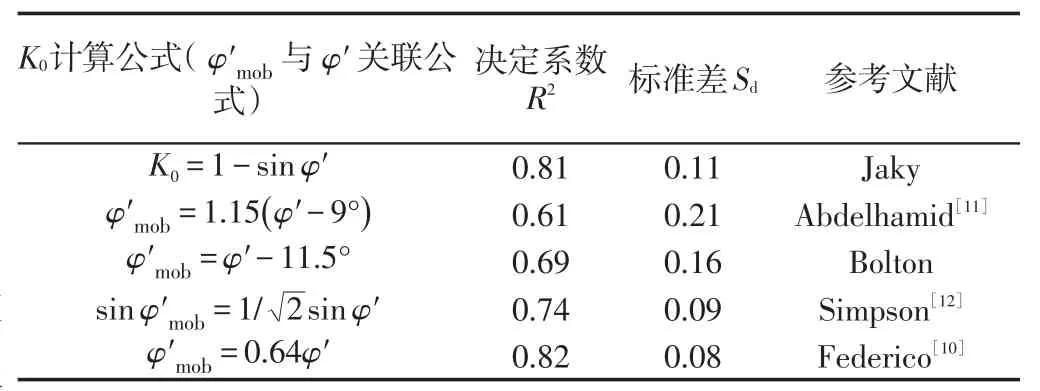
表1 不同K0公式R2与Sd的比较［10］Tab.1 Comparison between R2and Sdvalues relative to different K0equations

表2 考虑OCR的K0经验公式Tab.2 Empirical formulas for K0considering OCR influence

Okochi［18］利用双筒压力室三轴仪研究了影响K0固结试验结果的几个因素：（1）固结过程中出现的微小径向应变；（2）不同的初始应力状态：（3）在三轴压缩或伸长应力状态下的预先剪切；（4）不同的制样方法。结果表明，为了得到合理精确的试验结果，必须将整个试验过程中所产生的径向应变控制在一个相当小（±0.01%）的范围内。

姜朴［19］在普通三轴仪的基础上设计制作了双筒压力室，用光纤维位移传感器控制水位的变化来保持试样的侧向变形为0，实现了K0固结的功能。

Shamoto［20］基于双筒压力室三轴仪设计了控制应变增量比的应变路径试验（K0试验便是其中之一）并分析了仪器误差的来源，包括：加荷速率、环形水面面积以及薄膜渗透性，最后指出仪器无法进行试样膨胀条件下的应力路径试验这一不足。

Chen［21］研制了用于量测K0的大型土压力模型试验设备，研究了风干后松散堆积的Ottawa砂的K0值，并与Jaky公式进行了对比，吻合良好。

宋飞［22］为了研究砂土各向异性对K0的影响，制备了不同沉积方向的砂土试样，在研制应变路径试验设备的基础上给出了K0的测量方法，并将试验测得的K0与Jaky公式以及土压力离心模型试验结果进行了对比。

原位试验包括扁铲侧胀试验、旁压试验、原位应力铲试验、载荷试验等。

1.2 主动与被动土压力系数Ka、Kp

Rankine和Coulomb土压力理论是计算主、被动土压力的两种基本理论。Rankine理论假设土体是具有水平表面的半无限体、墙背竖直光滑，当墙后填土达到极限平衡状态时，与墙背接触的任一土单元体都处于极限平衡状态，然后根据土单元体处于极限平衡状态时应力所满足的条件来建立土压力的计算公式，最终得到Rankine理论的主动与被动土压力系数。Coulomb理论假定墙后填土达到极限平衡状态时的滑动面为平面、滑动体为刚性体，然后根据整个滑动土体上力的平衡条件来确定土压力，最终得到Coulomb理论的土压力系数。

王元战基于Coulomb理论的假设，在墙后填土滑动楔体上沿竖向取水平薄层作为微分单元体，通过作用在单元体上的水平力、竖向力和力矩平衡条件，建立了挡土墙上土压力强度的一阶微分方程式，求出了土侧主、被动压力系数的理论公式

式中：θ为滑动面与水平面的夹角；δ为填土与墙背之间的摩擦角；φ为填土内摩擦角。

章瑞文在前人研究的基础上，对墙背竖直、填土为砂土、填土面水平的刚性挡土墙在平移模式下，考虑土与墙背的摩擦所引起的主应力偏转，建立了主动状态下墙背处土侧压力系数的计算公式

式中：δ为土与墙背摩擦角；θ为主应力偏转角；当θ=0时，Ka与Rankine理论一致。

1.3 中间状态土压力系数

在K0的单元试验研究过程中，为了保证试样不产生侧向变形，许多学者设计了控制应变路径的试验设备。Gudehus等研制了等应变路径试验设备。Topolnicki等研制了应变增量比（侧向应变增量与轴向应变增量的比值）的控制范围为-1.0～1.0的平面应变双轴试验仪。Asaka等对常规三轴试验设备进行了改进，实现了等应变增量比的控制，其应变增量比的控制范围为-0.5～1.0。宋飞借鉴Asaka等的设备研制思路，在现有的三轴试验设备基础上增加了测量试样体变的传感器，进一步扩大了应变增量比的控制范围。

在控制应变路径的试验过程中，Gudehus等发现当砂土沿着应变增量比为常数的路径加载时，应力路径不管起点如何，最终都逼近于一条应力比为常数的直线，并将此常应力比所对应的应力状态称之为渐近状态。Chu和Lo通过应变增量比为常数的试验研究了渐近状态的应力比和应变增量比的关系，从图2的试验结果可以看出，当应变增量比保持为一个常数时，不管初始应力状态如何，最终都逼近一条应力比为常数的直线。

图2 应变增量比为常数时的应力路径（Chu）［34］Fig.2 Stress paths in the constant strain path test under different confining pressures

张建民在对应变路径试验结果观察分析的基础上，提出了平面应变条件下描述渐近状态应力比与应变增量比之间关系的数学表达式，并称之为渐近状态准则

式中：Rε为应变增量比，Kmin为某一Rε条件下的最终（最小）应力比。当Rε=0时，试样无侧向应变，Kmin=K0；当Rε=-1时，Kmin与朗肯理论的Ka、Kp相同。将Rε与挡墙位移Δ以某种函数相关联，便可得到土压力系数K与挡墙位移Δ的关系，即得到了中间状态土压力系数的计算公式。

周瑞忠等提出用Sigmoid函数对Rankine土压力理论进行改进，以使它更适合于非极限平衡条件下考虑结构与土体相互作用的影响。Sigmoid函数的基本形式如下

式中：i=0、α、p分别为静止、主动和被动的情况；sgn（x）为取变位值x的符号；|δi| 为3种情况下的位移量；x为参考点位移量；f（x）为任意位移状态的土压力系数。

2 板桩墙变位对土压力的影响

2.1 模型与现场试验研究

Rowe进行了一系列的板桩土压力模型试验研究，试验结果见图3。当在拉杆有足够的弹性变形条件下（变位约等于墙高的0.1%）进行试验时，土压力为三角形分布，与采用库伦土压力公式取δ=(2/3) φ得出的土压力分布相近，因而Rowe认为在板桩设计时可采用库伦土压力公式计算土压力；而当拉杆变形受限时，墙后主动土压力不同于经典土压力的三角形分布情况，主动土压力值在拉杆附近增大、而在跨中减小，然而主动土压力合力的大小与三角形分布的情形相近，由于拉杆处的应力集中和相近的合力大小，墙后主动土压力的实际合力作用点就比按三角形分布计算时的位置高，这将影响结构设计时所依据的弯矩平衡方程的正确性，导致设计参数的误差。

Fang和Ishibashi对砂填土刚性挡墙的主动土压力分布进行了模型试验，结果表明：主动土压力为非线性分布，具体的分布形式随挡墙变位方式的不同而改变，但达到主动土压力状态时，不同的挡墙变位方式所需的位移量基本相同，土压力的合力作用点会随着填土密度的增长而上升。

Endley分析了Freeport港口1986年建设的单锚板桩码头监测数据，包括板桩墙的变形、内力及锚杆位置下方三个测点的土压力数据，发现接近锚杆位置测点的土压力系数最大，随测点远离锚杆而逐渐减小，且土压力测值明显大于设计取值，这也导致了板桩的水平位移明显大于设计值，增加了码头使用过程中的风险。

图3 拉杆变位对板桩墙后土压力的影响（Rowe）［37］Fig.3 Influence of tie rod displacement to the earth pressure behind sheet pile wall

图4 砂土悬臂支护土压力变化过程（陆培毅）［40］Fig.4 Earth pressure in cantilever support

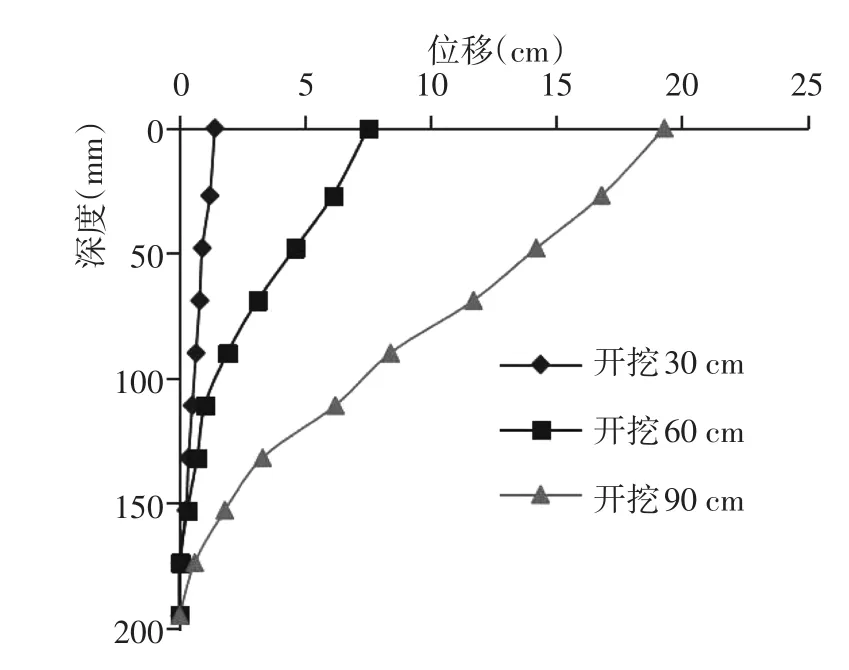
图5 砂土悬臂支护板桩位移（陆培毅）［40］Fig.5 Displacement in cantilever support

图6 土压力-位移实测曲线（聂宗泉）［41］Fig.6 Monitored earth pressure-displacement curves

陆培毅对回填砂土的悬臂与单支撑支护结构进行室内模型试验，模拟基坑的分阶段开挖过程，记录了整个过程中支护结构的侧向变形与受到的土压力变化，其中悬臂支护实测数据如图4、5。分析主动区土压力可见：基坑以上主动土压力试验值与理论值吻合较好；而在开挖面以下，土压力明显减小（与经验相悖）；支护底端由于嵌固作用，土压力又增大。分析被动区土压力可见：坑面附近实测值接近甚至超过理论值，而在约0.25倍基坑挖深以下，实测值远小于理论值。

聂宗泉对上海地铁M8线延吉中路站基坑主动区土压力和地下连续墙水平位移实测资料进行分析，发现两者近似为双曲线关系（图6）。

2.2 理论研究

2.2.1 土压力与位移的非线性关系

Terzaghi最早发现挡土墙需要有足够的位移才能使所受到的土压力达到主动或被动状态，并认为密实砂达到主、被动状态所需的挡墙位移分别为0.001 H和0.05 H，H为挡墙高。之后，许多学者通过模型试验来推测土压力达到极限状态所需的挡墙位移量，结果见表3。

表3 土体达到主动或被动极限状态时挡土结构所需位移量［35］Tab.3 Wall displacements required to develop active and passive earth pressures

Bang认为作用在挡墙上的土压力从静止到主动状态，是一个渐变的过程，提出了“中间主动状态”的概念，指出土压力计算应同时考虑墙体的变位方式和大小，并建立了挡墙绕墙趾转动时的主动土压力计算公式。

陈页开研究了非极限状态的土压力，并提出用指数函数描述挡土墙所受主动土压力与位移的关系，最终将所得成果应用于弹性地基梁法并将之改造，提出了柔性挡墙的墙侧土压力计算方法

式中：Pa、Pp为主、被动状态土压力；Ka、Kp为墙后地基反力系数；δ为墙体位移；Pacr、Ppcr分别为极限平衡状态下主和被动土压力；P0为静止土压力：δacr、δpcr为墙离开与挤向土体时极限平衡状态位移。

梅国雄根据土压力与挡土结构之间相互作用的机理分析，建立了如下考虑变形的土压力计算方法

式中：p0为静止土压力的一半；为内摩擦角的函数；b( ) sa,φ为主动土压力位移量和内摩擦角的函数，且有b＞0。对于k,b,p0等，可通过原位测试得到3个点后经反算得到。

之后，卢国胜、张文慧、曾玉莹、李超等学者均对挡土结构土压力与位移的关系进行了一定研究，各自建立了考虑位移的土压力计算公式，并分别与工程实测结果或有限元模拟结果对比，吻合结果良好，存在一定的应用价值。

2.2.2 板桩变位对土压力分布的影响

应宏伟针对鼓形变位模式的柔性挡土墙，采用库伦土压力理论的假设，挡土墙上的主动土压力假定由墙后填土在极限平衡状态下出现的滑动楔体产生，在该滑动楔体上沿填土深度方向取典型水平薄层单元进行分析，分段建立关于挡土墙上土压力强度的一阶微分方程，给出了鼓形变位模式下，柔性挡土墙上的土压力强度、土压力合力和合力作用点的理论公式，并与库伦理论和陆培毅试验结果进行比较分析（图7）。结果表明，鼓形变位模式下，土压力合力与库伦理论结果相等，但土压力分布和合力作用点位置明显不同；墙顶附近的土拱作用使土压力大致呈R形分布。

图7 应宏伟理论与库伦理论、陆陪毅试验数据的比较Fig.7 Comparison among earth pressure distributions for several methods

图8 刚性挡墙位移模式分析图（彭述权）Fig.8 Analysis of displacement modes of rigid retaining walls

彭述权等假定挡墙后填土沿墙高任一点处侧压力与其水平位移成线性关系，将土体看作是一系列弹簧和理想刚塑体的组合体。在此基础上分析了挡墙的位移模式，将不同位移模式表示为，式中：s下、s上分别是挡墙墙顶、底部水平位移。n从零变化到无穷大，可以描述挡墙的不同位移模式（图8）。通过改进Coulomb理论，提出了不同位移模式下刚性挡土墙主动土压力非线性分布计算方法，得到了不同位移模式挡墙土压力分布图（图9），与试验结果吻合较好。

图9 不同位移模式挡墙土压力分布图（彭述权）［55］Fig.9 Distribution of active pressure on retaining walls with different displacement modes

图10 土拱效应原理Fig.10 Soil arching theory

图11 主动状态土拱理论示意图（Handy）［57］Fig.11 Arching theory applied to active-state wall

2.2.3 土拱效应

Rowe用土拱效应来解释有锚板桩墙土压力的重分布现象。Terzaghi对土拱效应的定义是：“当支撑土体的一部分屈服时，屈服土体将从原有位置移出，屈服土体和邻近静止土体的相对移动将受到两部分土体间剪应力的阻碍作用，由于剪应力阻力有使屈服土体保留在原有位置的趋势，从而使屈服区域土压力减小而邻近静止土体土压力增大，这种土压力从屈服区域转移到邻近静止区域的现象通常称为土拱效应。有时，当屈服土体比邻近土体移动量更大时，也将发生土拱效应。”由此定义可知，土拱效应包含两部分内容：结构屈服部位土压力的降低和邻近位置土压力的增加（图10）。

Handy认为土拱效应是挡土墙与填土的摩擦所导致的土单元体小主应力方向的旋转（图11），且将土拱描述为旋转后的近似为悬链线的小主应力轨迹线，并基于以上理论推导了挡土墙平移模式下的主动土压力计算公式，与试验数据吻合良好。Harrop-Williams对悬链线形土拱进行了验证，并提出圆形土拱假设，在该假设的土拱轨迹上大小主应力均为常数。

Vaziri把影响土拱效应的因素归结为三个方面：（1）土拱效应引起的土压力变化随着土体刚度的增大而增长，且密实砂中增长幅度比松砂和粘土中大；（2）土拱效应随着支护结构的挠度增大而增大；（3）土拱效应随着锚固的屈服而减小。

土拱的量化为分析挡土墙后的土压力提供了一种新的思路，许多学者对此进行了研究。Paik假设挡土墙平移模式下的小主应力轨迹为圆弧，利用水平层析法，分析了该模式下主动土压力的分布规律，并推导了相应的计算公式。Goel 和Patra分别研究了墙后土体滑裂面为平面（Analysis1）和抛物面（Analysis2）、土拱轨迹为抛物线时的主动土压力计算公式，并与Tsagareli的模型试验数据以及前人的研究成果比较，结果（图12）。

图12 主动土压力及合力作用点高度理论计算结果与模型试验结果对比（Goel）［61］Fig.12 Comparison of active earth pressure and height of its application of proposed theory with experimental results

2.2.4 有限元模拟

Bjerrum等首先把有限单元法用于排桩墙，对不同排桩刚度和锚杆轴向变形条件下的土压力进行分析，结果与Rowe的模型试验结论一致。有限元法可以计算经历一系列预定应力历史的土压力与板桩变形的分布形式，这种功能让模拟不同的施工过程（开挖与回填）中桩土相互作用的变化规律成为了可能，使研究不仅仅局限于极限平衡状态。

Hashash和Whittle采用非线性有限元模拟基坑开挖工程，用详细的应力路径解释了粘土在地连墙上引起的土压力的发展过程，并着重讨论了开挖过程中引起的土拱效应。

Bilgin采用有限元法分析了不同墙高与不同填土相互组合的12种情况下，不同的施工过程对板桩土压力、变形、弯矩及锚固力的影响，并拟合出了考虑锚碇处应力集中的开挖结束后板桩墙后土压力系数的分布公式

式中：KA，N、KP，N为推荐的主、被动土压力系数；KA-conv、KP-conv为库伦理论土压力系数；H为板桩泥面以上墙高；D为入土深度；z为计算点距墙顶的长度；d为计算点在泥面以下的深度。

虽然有限元法的优越性有目共睹，但要真实地模拟实际工程的工作状态也并非易事。Grande和Potts的研究就反映出了有限元法的一些难点——如何确定土体的本构模型和边界条件。因此，物理模型试验在研究各种不同边界条件的工程问题上仍是非常有效的手段，同时还能验证理论和数值研究所得到的结论。Tefera利用大型单锚板桩模型试验所得到的数据反推有限元模型参数，并进行相应的数值模拟，得到的结果与试验数据吻合良好，可见模型参数的正确与否是有限元计算的关键。

3 结论

本文从土体侧向变形对土压力系数的影响出发，进一步归纳总结了板桩墙变位对墙后土压力分布的影响规律，成果如下：

（1）采用以有效内摩擦角φ′为参数的经验公式估算正常固结土的静止土压力系数K0因其历史长远、形式简单而常被工程设计所采用；但φ′与K0各自所代表的土体状态并不一致，因此用φ′来估算K0缺乏一定的理论依据；已激发内摩擦角φ′mob的提出解决了这一问题，用同样表示未达到极限状态的φ′mob来估算K0有一定的理论支撑，与试验数据也吻合良好。

（2）超固结土的K0估算常采用正常固结土K0（一般为Jaky公式）与OCR共同组成的经验公式，与OCR的关系一般为线性或指数函数形式。

（3）经典土压力理论对主动和被动极限状态土压力系数Ka、Kp的研究较为成熟，目前对Ka、Kp的研究多是对经典土压力理论假设的完善或基于其基本假设提出新的分析方法。

（4）渐近状态应力比Kmin与应变增量比Rε关系的发现为估算处在主动与被动极限状态之间的中间状态土压力系数提供了一种途径，应变增量比Rε为联系土压力系数K与挡墙位移Δ的中间变量。

（5）针对板桩或挡土墙后土压力的模型试验与理论研究均得出挡土结构的变位会使土压力分布形式改变的结论，且具体的分布形式随变位方式的不同各异，在有锚结构中，锚碇支撑附近的土压力会产生局部应力集中的现象。

（6）利用具有相近变化特性的函数对土压力与位移实测数据进行拟合是得到两者非线性关系的一种较为容易的方法，且针对某一具体工程特定土壤类型的性质预测能得到吻合度较高的结果。

虽然国内外学者已对土压力系数受土体侧向变形的影响及土压力分布随板桩墙变位的变化规律做了大量研究，取得了丰硕的研究成果，但以下几方面仍需进行深入的研究和探讨。

（1）控制应变路径的单元试验能够对板桩墙后土单元体的变形进行模拟，因此，确定合适的应变路径试验方案，研究试验过程中土样力学特性的变化，是分析板桩墙后土压力随墙体变位而变化的有效途径，值得深入研究和探讨。

（2）土拱效应的量化为分析挡土墙后的土压力提供了一种新的思路，但目前其应用范围仍局限于土体达到极限状态时出现滑楔体假设的情况，如何量化非极限状态时的土拱效应有待进一步研究。

（3）模型参数的正确与否是有限元计算的关键，如何近似地确定土体的本构模型、简化问题的边界条件仍需进行深入的研究。

［1］韩理安，席与耀.港口水工建筑物［M］.北京：人民交通出版社，2008.

［2］郦能惠.国外板桩土压力模型试验研究［J］.水利水运科技情报，1975（6）：28-47.

［3］Brooker E W，Ireland H O.Earth pressures at rest related to stress history［J］.Canadian Geotechnical Journal，1965，2（1）：1-15.

［4］Fraser A M.The influence of stress ratio on compressibility and pore pressure coefficients in compacted soils［D］.London：Imperial College London，1957.

［5］Burland J B，Roscoe K H.Local strains and pore pressures in a normally consolidated clay layer during one-dimensional consolidation［J］.Geotechnique，1969，19（3）：335-356.

［6］Matsuoka H，Sakakibara K.A constitutive model for sands and clays evaluating principal stress rotation［J］.Soils and Foundations，1987，27（4）：73-88.

［7］史宏彦，谢定义，汪闻韶.确定无粘性土静止土压力系数的一个理论公式［J］.水利学报，2001（4）：85-88. SHI H Y，XIE D Y，WANG W S.A theoretical formula determining the coefficient of earth pressure at rest for cohesionless soil［J］. Journal of Hydraulic Engineering，2001（4）：85-88.

［8］强跃，赵明阶，林军志，等.静止土压力系数探究［J］.岩土力学，2013，34（3）：727-730. QIANG Y，ZHAO M J，LIN J Z，et al.Research on coefficient of earth pressure at rest［J］.Rock and Soil Mechanics，2013，34（3）：727-730.

［9］Taylor D W.Fundamentals of soil mechanics［J］.Soil Science，1948，66（2）：161.

［10］Federico A，Elia G，Germano V.A short note on the earth pressure and mobilized angle of internal frictional in one-dimensional compression of soils［J］.Journal of Geoengineering，2008，3（1）：41-46.

［11］Abdelhamid M S，Krizek R J.At-Rest Lateral Earth Pressure of Consolidating Clay［J］.Journal of the Geotechnical Engineering Division，1976，102（7）：721-738.

［12］Simpson B.Retaining structures：displacement and design［J］.Géotechnique，1992，42（4）：541-576.

［13］Kenney T C.Discussion on Proc.［J］.Proc.ASCE，1959，85（3）：67-79.

［14］Alpan I.The empirical evaluation of the coefficient K0and K0R［J］.Soil and Foundation，1967，7（1）：31-40.

［15］Hanna A，Al-Romhein R.At-rest earth pressure of overconsolidated cohesionless soil［J］.Journal of Geotechnical and Geoenvironmental Engineering，2008，134（3）：408-412.

［16］Meyerhof G G.Bearing Capacity and Settlement of Pile Foundations［J］.Journal of the Geotechnical Engineering Division，1976，102（3）：195-228.

［17］Mayne P W，Kulhawy F H.K0OCR relationships in soil［J］.Journal of the Geotechnical Engineering Division，1982，108（6）：851-872.

［18］Okochi Y，Tatsuoka F.Some factors affecting K0-values of sand measured in triaxial cell［J］.Soils and Foundations，1984，24（3）：52-68.

［19］姜朴，宋永祥.K0固结三轴仪的研制与试验研究［J］.岩土工程学报，1991，13（3）：43-52. JIANG P，SONG Y X.Development and experiment of K0-consolidation triaxial apparatus［J］.Chinese Journal of Geotechnical Engineering，1991，13（3）：43-52.

［20］Shamoto Y，Zhang J M，Kusukame T.A simple method for triaxial strain path testing［J］.Soils and Foundations，1996，36（2）：129-137.

［21］Chen T J，Fang Y S.A new facility for measurement of earth pressure at-rest［J］.Geotechnical Engineering，2002，33（3）：113-131.

［22］宋飞，张建民，刘超.各向异性砂土K0试验研究［J］.岩土力学，2010，31（12）：3 727-3 732. SONG F，ZHANG J M，LIU C.Experimental study of K0of anisotropic sand［J］.Rock and Soil Mechanics，2010，31（12）：3 727-3 732.

Review on influence of sheet pile wall lateral displacement on earth pressure

CHEN Da1,WANG Xiao1,YANG Yi⁃chen1,2,DENG Yong⁃feng3
（1.College of Harbor,Coastal and Offshore Engineering,Hohai University,Nanjing 210098,China;2.Shanghai Waterway Engineering Design and Consulting Co.,Ltd.,Shanghai 200120,China;3.Institute of Geotechnical Engineering,School of Transportation,Southeast University,Nanjing 210096,China）

Sheet pile wharf has been widely used in coastal and inland areas for its advantages such as structure simplicity,constructing convenience and suitability of complicated geological conditions etc.Conventional design methods assume that earth pressure in front of and behind a sheet pile wall achieve the passive and active critical states,respectively.However,the lateral deformation and displacement of the entire wall are restricted to a variable extent due to the combined effects of soil and anchor structures during the construction and service periods. Hence,the actual earth pressure is not in the critical state which could lead to conservative project design with waste of cost or rash one with hidden danger.Therefore,many researchers studied the influence of lateral deformation and displacement on the earth pressure in front of and behind a sheet pile wall,and many results were obtained. In this paper,the state of the influence of lateral deformation of soil on earth pressure coefficient and displacement of the sheet pile wall on earth pressure were reviewed to summarize the main conclusions.Finally,some suggestions on the direction of future research were presented.

sheet pile wall;deformation;displacement;earth pressure coefficient;earth pressure

TV 313

A

1005-8443（2016）01-0071-10

2015-05-18；

2015-06-23

陈达(1978-)，男，福建福清人，教授，主要从事港工结构方面研究。

Biography：CHEN Da（1978-），male,professor.