非线性系统精确线性化的微分几何法

孙建红

(忻州师范学院 五寨分院数学系，山西 忻州 036200)



非线性系统精确线性化的微分几何法

孙建红

(忻州师范学院 五寨分院数学系，山西 忻州 036200)

非线性系统是普遍存在的一种系统，从数学角度可以用非线性微分方程加以描述。在实际应用中，非线性系统的线性化必然会带来误差。本文讨论了一种非线性系统的完全线性化方法，采用微分几何理论，通过坐标变换和状态反馈变换等方式，实现非线性系统的精确线性化。

非线性系统；精确线性化；微分几何法

传统的非线性系统分析以及系统控制方法中，多数是针对某个工作点进行线性化，然后通过线性系统理论展开研究。这种传统线性化方法中，工作点的选择决定了线性化的精度。近似线性化方法无法对强非线性大范围变化的系统提供有效分析。

近年来，非线性系统的反馈线性化受到越来越多的关注，也是人们常用的一种非线性系统控制设计方案。精确线性化是反馈线性化中一种非常典型的线性化方法，在精确线性化方法中，逆系统方法和微分几何法分别形成了各自的理论体系，并且在各个领域都有广泛应用。

微分几何法主要是通过微分流形概念，利用微分同胚变换以及反馈变换来实现非线性系统精确线性化的目标。理论上讲，精确线性化方法不存在误差，它是通过严格的状态变换和反馈变化来实现线性化，在操作过程中没有忽略高阶非线性化，所以将这种方法称为精确线性化。本文阐述了微分几何法的基本方法理论，并分析了非线性系统精确线的处理过程，为微分几何法的广泛应用提供理论支撑。

1 非线性系统控制方法回顾

1.1 几种代表性非线性方法

非线性系统具有极强的复杂性和多样性，无法建立一种具有普遍性的非线性系统控制理论[1]。所以，要通过有效的方式将非线性系统线性化，下面就介绍几种具有代表性的方法：

(1)经典方法

针对特殊系统，提出以下三种基本的理论方法，第一是针对二阶非线性系统提出的相平面法；第二种是针对非线性环节提出的描述函数方法；第三种是针对某个特定非线性元件提出的绝对稳定性理论。

(2)Lyapunov方法

这是一种比较完善的一般化非线性方法，也因为Lyapunov方法具有较强的一般性，所以在分析稳定性方面缺乏构造性。

(3)非线性系统变结构方法

可以将非线性系统的变结构控制方法称为“具有活动模态的变结构控制”。这种方法起源于上世纪50年代，滑动模态对摄动和干扰具有不变性，这是一种非常实用的综合控制方法，具有良好的性能品质[2]。

(4)微分代数方法和微分几何方法

从20世纪70年代发展起来的微分代数和几何方法，对解决非线性系统控制理论问题具有积极作用，在促进理论发展的同时，实现了理论到实践的飞跃[4]。

(5)智能控制理论方法

现在有越来越多的控制采用智能控制方法，例如遗传算法、神经网络控制以及基因控制等，可以利用智能控制方法设计非线性识别系统、鲁棒镇定等控制器的设计。

1.2 非线性控制系统的精确线性化方法

非线性的精确化控制体系中，对于满足特定条件的非线性系统，采用同胚变换和非线性局部变换的方法，让非线性系统流形中的全局或者局部坐标转变为线性结构，这种方法的最大优势就是不会引入新的系统误差，非线性到线性化前后的拓扑结构是一致的[3]。传统非线性精确线性化的方式就是将非线性的局部或者全局转变为可控标准的线性系统。如果不满足线性化条件，那么通过状态反馈和同胚变换的方式将系统分解，分解之后的一个部分依旧是非线性形式，另一个部分是可控标准型线性化模式，这种方式也得到了广泛应用[5-6]。

本文希望通过非线性系统精确化的分析和改进，拓宽精确线性化的条件，利用现代控制理论中的非线性方法解决精准线性化带来的问题。

2 数学预备知识

2.1 欧氏空间中的可微映射

可以将n维的欧氏空间标记为Rn，U是Rn的一个子集，并且F:U→R代表一个函数。可以将f在点x(x1,…,xn)处的值标记为f(x)=f(x1,…,xn)。

定义2.1 若f是一个可微映射，那么它的每一个阶都存在导数。如果f是一个解析映射，同时也是可微映射，并且存在x0∈U，那么存在领域V让f在x0处的泰勒展开收敛于f(x0)。

将映射F:U→R定义为(f1,…,fn)，那么f1:U→R，i=1,…m。映射F为可微的，那么fi(i=1,…m)都属于可微的。

假设U∈Rn,V∈Rm都属于开子集，那么映射F:U→V在x∈U范围内的Jacobi矩阵可以定义为：

(2-1)

可以将JF(x)在点x=x0处的取值表示为JF(x0)。

定义2.2 将映射F:U→V称为微分同胚，如果满足以下两个条件：首先是F在U上具有一一对应的值；其次是F以及F的逆映射F-1都属于可微映射，那么可以将可微映射F在x0定义为rankJF(x0)。如果F四微分同胚，那么JF(x)就是满秩的方阵。

2.2 微分流形

微分流形属于一种非常特殊的拓扑结构，空间范围更加广泛，可以在研究拓扑结构的基础上对曲面几何性质展开研究，微分流形的定义如下所示：

定义2.3 假设X属于一个非空的集合，τ是X其中的一个子集组，如果子集能够满足下述条件那么就可以将这个子集称作是X中的一个拓扑结构：

(1)x∈τ,∅∈τ；

(2)τ中的任意多个集的并运算属于τ；

(3)τ中的任意多个集的交运算属于τ；

如果上述条件同时满足，那么将τ中的元素称作是开集。

X是一个非空集，在其中定义的τ就可以称作是拓扑空间，将该空间记为(x,τ)。如果τ已经确定，也可以将拓扑空间记为X。

如果开集和G∈τ之中包含了点p，且p∈X，那么可以将G认为是p其中的一个开领域。

假设(X,τ)属于第一拓扑空间，那么τB属于X的一个开集组，也可以将其记为τB⊂τ。如果可以将每一个开集G∈τ都表示为τB之中的特定开空间，那么τB就是τ的一个基。

假设X1和X2是二拓扑空间，F是X1到X2的映射，假设X2中存在任意的开集U2，U2的逆像集F-1(U2)属于空间X1的开集，那么可以将F称作是连续映射。假设X1中的任意一个开集U1，U1的像集F(U1)是X2的开集，那么可以将F看作开映射。如果F不仅是开映射，同时也是连续映射，那么可以将F称为同胚映射。

定义2.4 拓扑空间X为n维局部欧氏空间，如果对于∀x∈X，存在一个x的开邻域，有Ux⊂X以及ψ:Ux→Rn映射，他们满足两个的条件(1)ψ(Ux))属于Rn中的一个开子集；(2)ψ属于Ux到ψ(Ux)的一个同胚映射。

定义2.5 定义n维流形M属于n维局部欧氏拓扑空间，具有可数的基底。流形M上的一个坐标图是(U,φ)，U是空间中一个开集，φ是从U到φ(U)中的一个同胚映射。在特殊情况下，也可以将φ用φ=[φ1,…,φn]来表示，φ:U→R就是空间中的第i个坐标函数。如果p∈U，那么φ(p)=[φ1(p),…,φn(p)]就是坐标图中的一个局部坐标。

假设(V,ψ)和(U,φ)是流形M上的两个坐标图，并且U∩V≠∅，将其称为同胚映射：

ψ-1φ：φ(U∩V)→ψ(U∩V)

(2-2)

式2-2是U∩V上的一个坐标变换，对于任意一个p∈U∩V，将任意的一个局部坐标[φ1(p),…,φn(p)]映射称为坐标[ψ1(p),…,ψn(p)]。

假设M是一个n维的流行，(V,ψ)和(U,φ)称作是C∞-相容的，如果U∩V≠∅，那么ψ-1φ就是微分同胚。

定义2.6 微分流形M是一个定义了完备的C∞-图册A°的流形，将其记为(m,A°)。

可以证明M流形上的任意一个点的局部坐标维数和坐标图的选择并没有关联，将其称作M在该点的维数。

2.3 微分几何法的概念和意义

2.3.1 概念和定义

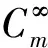
定义2.7 假设M和N是两个微分流形，在二者之间存在一个C∞的映射F，并且这个可逆映射也是C∞的，那么就可以将F看作是M和N的微分同胚。在微分几何理论之中，也可以将两个局部坐标的领域之间的坐标变换看作是微分同胚。

定义2.8 假设h(x)∈C∞(M)，那么可以定义C∞函数h(x)的对于向量场f的李导数是：

(2-3)

在此基础上，可以将多重李导数定义为：

Lf(h)=Lf(Lfk-1(h))

(2-4)

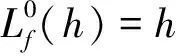
定义2.9 假设f(x),g(x)∈V(M)，那么可以得出向量场g对于向量场f的李导数如下式所示：

Lfg

(2-5)

(2-6)

该矩阵的多重李导数表达式为：

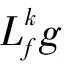
(2-7)

2.3.2 非线性系统线性化描述

可以利用下述方程对n维的C∞微分流形上的仿射非线性系统进行描述：

(2-8)

上式中，f(x),g1(x),…,gm(x)代表的分别是光滑向量场(f(x),g1(x)∈V(M))；h1(x),…,hm(x)代表的是光滑函数hm(x)∈C∞(M)。可以将上述的方程组进一步转换成：

(2-9)

y=h(x)

上式中，u=(u1,…,um)τ，y=(y1,…,yn)τ，g(x)=(g1(x)),…,gm(x))代表的是n×m矩阵，h(x)=(h1(x),…,hm(x))τ代表的是m维向量。完全线性化问题，实质上就是寻找一个非线性变换和一个反馈变换，z=∅为非线性变换，u=α(x)+β(x)υ为反馈变换，通过这两个变换可以让上述矩阵转换为一个完全可线性化的系统，该系统用下述公式表示：

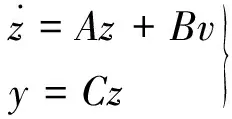
(2-10)

在上式中，A、B、C矩阵分别表示:

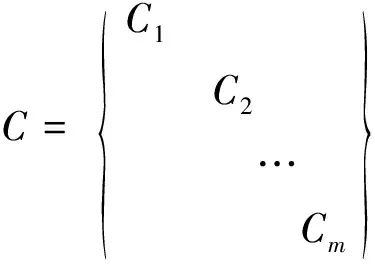
ri×1,Ci=(1,0,…,0)

如果上式中展示的非线性变换和反馈变换同时存在，那么可以认为公式(2-8)是完全线性化的。

假设多个变量的非线性系统可以按照下列方程表示：

(3-1)

yi=hi(x)(i=1,…,m)

并且系统的相对阶次向量为(r1,…,rm)，也就是说ri是满足下列条件的最小整数，

LgLfr1-1hi(x)(LgiLfr1-1gi(x),…,LgnLfr1-1hi(x))≠0)，其中x∈M

(3-2)

在此基础上构造函数矩阵，分别是n×m的D(X)矩阵和m×1的E(x)矩阵，

D(X),

E(x)

(3-3)

u=α(x)+β(x)v=-[D(X)]-1E(x)+[D(X)]-1v

(3-4)

可以与之构成一个闭环系统

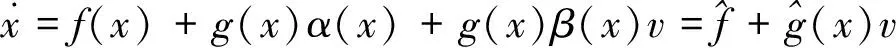
(3-5)

yi=hi(x) 其中i=1,…,m

将其转换成为线性系统，根据(3-3)，(3-4)和(3-5)，可以得出以下推论：

(3-6)

(3-7)

根据系统的相对阶次以及非齐次性来说，可以证明dhi，dLfhi…dLfri-1hi(i=1,…,n)是M上的n个线性无关微分。{zi}也就是M上的一个局部坐标，根据(3-5)、(3-6)和(3-7)可以推论出下列式子：

(3-8)

因此，在局部坐标中，可以将闭环系统转变为：

(3-9)

(3-10)

在这种情况下，系统已经完全从非线性化转换为线性化，并且还进一步被解耦成为m个子系统，这些子系统属于线性化、能控化系统。

(4-1)

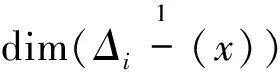
(4-2)

的结构，上式中：

Ai=[010︙⋱⋱︙⋱1︙00︙………………φi]}ri

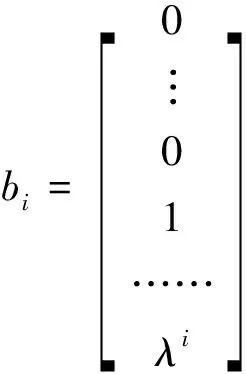
(4-3)

上式中，满足ri+li=pi,φi和λi是任意一个(li×ri)和(li×1)的常数矩阵和常向量。所以，目前的系统已经完全线性化，而且系统已经被解耦成为n个子系统，各个子系统都是线性的，并且为可控系统。

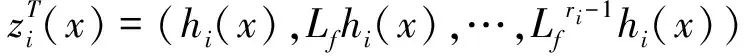
(4-4)

(4-5)

其中i=1,…,m。

经过比较分析，可以得出

(4-6)

将(3-2)、(3-3)、(3-4)和(3-5)经过综合分析，可以得出：

(4-7)

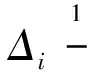
5 结束语

在工程应用的过程中，非线性系统线性化是非常普遍的方法，也是处理非线性问题常用的方法之一。经典线性化方法是将非线性系统在特定的点做泰勒展开分析，然后选取近似相近点。但是这种方法之中存在误差，这种误差也会逐渐扩大，所以需要一种精确度更高的线性化方法。本文介绍了常见的非线性系统线性化方法，采用微分几何理论展开分析，其比较突出的优势就是可以实现系统精确线性化，可以将多变量耦合转变为解耦。这种非线性的线性化方法可以获得更好的效果，并且有效降低误差。这种非线性精确线性化的微分几何方法在计算机领域的应用不断扩大，在实际应用领域也有更加广阔的应用前景。

[1]周兆敏.非线性系统的线性化方法[J].电气传动,1989(4):42-46.

[2]陈冲.非线性几何法解藕研究及在交傀调速系统中应用[D].哈尔滨工业大学博士论文.1991.

[3]钟宁帆.非线性系统精确线性化方法研究[D].南京理工大学.2004.

[4]安祎春.非线性控制系统解耦及精确线性化[D].东北大学.2006.

[5]乐江源.Boost变换器精确反馈线性化滑膜变结构控制[J].中国电机工程学报,2011(10):51.

[6]许志龙.基于精确线性化和变结结构方法的航空发动机非线性控制研究[J].变频器世界,2015(9):29-31.

[责任编辑：张怀涛]

2016-09-20

孙建红(1977-)，男，山西忻州人，讲师，主要从事基础数学和微分几何的研究。

O186

A

1671-5330(2016)05-0053-06