执行器饱和时滞系统的状态反馈控制

姚合军，袁 野，乔 玥，袁付顺

(安阳师范学院 数学与统计学院，河南 安阳 455000)



执行器饱和时滞系统的状态反馈控制

姚合军，袁 野，乔 玥，袁付顺

(安阳师范学院 数学与统计学院，河南 安阳 455000)

研究了一类执行器饱和时滞系统的状态反馈控制问题。基于Lyapunov稳定性理论，利用线性矩阵不等式方法，给出了系统全局渐近稳定的充分条件和状态反馈控制器设计方法。通过在Lyapunov函数中引入参数矩阵，降低了所得稳定条件的保守性。

执行器饱和；时滞系统；线性矩阵不等式

1 引言

饱和现象广泛地存在于各种动力系统中，如果不考虑饱和限制，那么严重情况下将导致系统性能下降甚至不稳定。在实际工程控制过程中，控制输入往往需要满足一定的条件，而执行器饱和是一种最为常见的约束控制，因此有关于执行器饱和的研究具有非常重要的实际意义。自上世纪60年代Fuller[1]首次提出饱和系统以来，执行器饱和控制问题得到了众多学者的广泛关注[2-3]。Hu等人在文献[4]中针对带有执行器饱和的离散系统，利用饱和非线性特性，提出了凸组合的处理方法，通过引入辅助矩阵将稳定条件转化为线性矩阵不等式，得到了系统稳定性条件和控制器设计方法。随后Zhou等人把饱和系统的设计方法引入到饱和网络控制系统中来，如文献[5]，研究了饱和网络系统的输出反馈镇定问题。接着，又有一部分学者对带有饱和约束的时滞系统进行了研究。张美玉等人对具有非线性执行器饱和的时滞切换系统进行研究，结合线性矩阵不等式方法设计了系统状态反馈控制器[6]。陈东彦，司玉琴等人研究了多输入多输出饱和时滞系统的全局渐近稳定性问题，通过迭代算法进行吸引域估计。然而上述文献对饱和时滞系统的研究过程中所设计的Lyanpunov函数缺少恰当的参数矩阵，所得结果具有较大的保守性。正因为此，本文就是在前人研究的基础上，针对一类具有执行器饱和的时滞系统，基于Lyapunov稳定性理论，利用线性矩阵不等式方法，通过在Lyapunov函数中引入参数矩阵，得到了保守性较小的系统渐近稳定的充分条件和状态反馈控制器设计方案。

2 问题描述

考虑下面具有输入饱和的时滞系统：

x(t)=φ(t)t∈[-d,0]

(1)

其中x(t)∈Rn是状态向量，u(t)∈Rm是控制输入向量，A,Ad∈Rn×n是系统矩阵，B∈Rn×m是控制输入矩阵，φ(t)=[φ1(t)φ2(t)…φn(t)]T∈Rn是给定的系统初始状态，d是系统状态时滞，饱和函数sat(u(t))=[sat(u1(t)),sat(u2(t)),…,sat(um(t))]，具有如下形式：

本文旨在设计系统(1)的状态反馈控制器：

u(t)=2Kx(t)

(2)

其中K∈Rm×n是待定的常数矩阵。把(2)代入系统(1)中得到闭环系统：

x(t)=φ(t)t∈[-d,0]

(3)

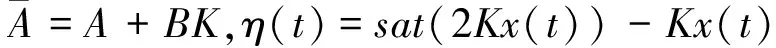
ηT(t)η(t)≤xT(t)KTKx(t)

(4)

设计目的是确定形如(2)的控制器，使闭环系统(3)是渐近稳定的。

(1)S<0

3 主要结果

定理1：如果存在常数ε>0，对称正定矩阵P,Q∈Rn×n和矩阵K∈Rm×n使得下面矩阵不等式

Θ=[ ATP+P A+Q+εKTKPAdPB∗-Q0∗∗-εI]<0

(5)

成立，则闭环系统(3)是渐近稳定的。

证明：选取Lyapunov函数

P,Q∈Rn×n是待定的对称正定矩阵。

V(t)沿系统(3)求导得到

+2xT(t)PBη(t)+xT(t)Qx(t)

-xT(t-d)Qx(t-d)

=φT(t)[P A+ ATP+QPAdPB∗-Q0∗∗0]Φ(t)

(6)

其中

由(4)式得到：

0≤ΦT(t)[εKTK00∗00∗∗-εI]Φ(t)

其中ε是任意小的一个正数。

把上式带入(6)式得到

其中

Θ=[ ATP+P A+Q+εKTKPAdPB∗-Q0∗∗-εI]

由Lyapunov稳定性理论知道当条件(5)成立时，闭环系统(3)是渐近稳定的。

[AX+B K+XTAT+ KTBT+ QAdX εB KT∗- Q00∗∗- εI0∗∗∗- εI]<0

(7)

证明：由引理1知道不等式(5)等价于

[P A+ ATP+QPAdPBεKT∗-Q00∗∗-εI0∗∗∗-εI]<0

上式左右两边分别乘以分块对角矩阵diag{P-1,P-1,ε-1,ε-1I}得到：

[ AP-1+P-1 AT+P-1QP-1AdP-1ε-1BP-1KT∗-P-1QP-100∗∗-ε-1I0∗∗∗-ε-1I]<0

[(A+BK)P-1+P-1(A+BK)T+P-1QP-1AdP-1ε-1BP-1KT∗-P-1QP-100∗∗-ε-1I0∗∗∗-ε-1I]<0

4 结论

本文给出了一类带有执行器饱和的时滞系统的渐近稳定条件和状态反馈控制设计方法，通过在Lyapunov函数中引入参数矩阵，降低了系统稳定条件的保守性。

[1]A.T.Fuller.Inthelargestabilityofrelayandsaturatingcontrolsystemswithlinearcontrollers[J].InternationalJournalofControl, 1969，10(4):457-480.

[2]WangCL.Semi-globalpracticalstabilizationofnonholonomicwheeledmobilerobotswithsaturatedinputs[J].Automatica, 2008,44(3): 816 - 822.

[3]HuTingshu,LinZongli,ChenBenM.Ananalysisanddesignmethodforlinearsystemssubjecttoactuatorsaturationanddisturbance[J].Automatica, 2002,38(2):351-359.

[4]HuTingshu,LinZongli,ChenBM.Analysisanddesignfordiscrete-timelinearsystemssubjecttoactuatorsaturation[J].Systems&ControlLetters, 2002,45(2):97-112.

[5]ZhouRujuan,ZhangXiaomei,ShiGuiyin.Outputfeedbackstabilizationofnetworkedsystemssubjecttoactuatorsaturationandpacketdropout[J],LectureNotesinElectricalEngineering, 2012,136:149-154.

[6]张美玉, 刘玉忠. 具有非线性执行器饱和的时滞切换系统的控制器设计[J]. 沈阳师范大学学报, 2009,27(2):144-147.

[7]陈东彦，司玉琴.具有饱和状态反馈离散时滞系统的渐近稳定性[J].自动化学报，2008,34(11)：1445-1448.

[8]俞立. 鲁棒控制-线性矩阵不等式处理方法[M]. 北京:清华大学出版社,2002.

[责任编辑：张怀涛]

State Feedback Control for a Class of Time-delay Systems with Actuator Saturation

YAO He-jun, YUAN Ye, QIAO Yue, YUAN Fu-shun

(School of Mathematics and Statistics, Anyang Normal University,Anyang 455000,China)

The problem of state feedback control for a class of time-delay systems with actuator saturation is considered in this paper. Based on the Lyapunov stability theory, the stability condition and the state feedback controller design method are obtained by using the linear matrix inequality approach. By introducing the matrix into Lyapunov functional, the proposed conditions are less conservative than the previous results.

Actuator Saturation; Time-delay Systems; Linear matrix inequality

2016-08-26

国家自然科学基金项目(61073065)；国家级大学生创新创业训练项目(201610479045)；安阳师范学院大学生创新基金项目(ASCX/2016-Z113)

姚合军(1980-)，男，副教授，主要从事网络控制系统、饱和系统、变结构控制等方面的研究。

TP273

A

1671-5330(2016)05-0046-03