牙颌点云数据的显著性特征提取①
陈玲玲, 杨 玲, 谯舟三, 陈文乐
1(成都信息工程大学 电子工程学院, 成都 610225)2(中国气象局 大气探测重点开放实验室, 成都 610225)
牙颌点云数据的显著性特征提取①
陈玲玲1,2, 杨 玲1,2, 谯舟三1, 陈文乐1,2
1(成都信息工程大学 电子工程学院, 成都 610225)2(中国气象局 大气探测重点开放实验室, 成都 610225)
随着激光扫描测量技术的发展, 其数据测量精度的逐渐增高使得获取的几何模型表面点云数据的细节信息越丰富, 能更准确的反应物体几何表面特征, 但如此海量的点云数据同时也带来对应的技术挑战, 海量的点云数据在计算机文件存储、数据后期进一步处理以及软件可视化方面都不方便且效率低下. 本文中的算法首先采用栅格法对点云进行空间划分及领域关系的建立, 其次利用局部表面拟合的方法估算点云法向量, 然后利用点云K领域法的向量求解坐标点的显著性值, 最后根据显著性的值构建点云八叉树. 该算法实现了对点云显著性特征的提取和对点云数据量的进一步简化, 它不仅保留了对点云细节特征保持方面的优势, 而且在时间效率上得到了提高.
点云数据; 可视化; 显著性特征; 三维配准; 网格化重建
目前国内外针对点云数据集的精简算法可以分为两类, 第一: 通过对点云网格化处理后基于网格的精简算法; 第二: 基于对采集数据直接处理的点云精简方法. 前者方法首先通过对采集数据进行网格化三角剖份, 利用四面体模型表面的点、边和面之间相互关系拓扑数据压缩方法, 该算法中首先需要对散乱点云进行Delaunay三角剖份, 其整个时间复杂度较高, 算法效率较低. 而后者直接针对数据的精简算法既具有时间复杂度较低等优点, 并且操作简单. 主要有直接随机采样精简、基于包围盒空间划分方法、基于均匀网格划分的随机抽样法和基于高斯曲率和主曲率的精简算法.
2001年LEE KH[1]等人提出利用被测数据法向信息, 对采集数据空间包围盒栅格划分, 在单个空间格中选择特征点, 从而完成数据精简. 2002年DYN[2]等人提出的基于双变量适应性数据精简算法可以达到与被测物体模型表面接近的效果而高效精简数据. 2004年洪军[3]等人在通过相关研究基础上, 提出的同时利用改进型系数的空间包围盒法和基于角度-弦高简化法的合成数据精简算法, 取得较好的数据压缩效果. Pai-Feng Lee等在2006年提出了基于共面标准的八叉树细分点云简化算法. 2009年Hao Song[4]通过在对模式识别算法研究基础上提出的通过构造Voronoi图的全局聚类采样算法, 能有效地保留了点云中的边界特征, 去除非边界数据的非特征点, 但该算法容易产生数据删除孔洞, 容易误删除部分特征点, 且速度仍有待提高. 史宝权[5]等人提取了利用模式识别算法原理的基于聚类的点云特征保存数据精简方法. 2009年黄文明[6]等人提出的保留几何特征的散乱点云简化方法,在论文特定条件下取得较好的特征提取效果. 张欣[7]等人在2012年提出的基于特征保留的三角形折叠网格简化算法, 但该算法没有针对数据轮廓特征进行处理, 一定程度上依赖网格划分结果. Yitian Zhao在2012年提出基于法向夹角和高斯曲率结合的点云精简算法, 通过算法效果验证得出该算法具有较好的效果. Nira DyT[8]通过构造了—个非负度量函数平均每个数据点的权重分配, 这种算法能够有效去除非特征点,误差删除较小, 但由于反复迭代计算导致其效率较低.
针对上述算法各自的应用特点, 本文在研究二维图像显著性区域轮廓检测算法基础上引申到点云数据特征提取中, 提出一种基于显著性标准衡量的牙颌点云特征提取精简算法. 该算法首先采用栅格法对点云进行空间划分及领域关系的建立, 其次利用局部表面拟合的方法估算点云法向量, 然后利用点云K领域法的向量求解坐标点的显著性值, 最后根据显著性的值构建点云八叉树, 从而实现对点云显著性特征的提取,最终做到进一步精简数据量.
1 牙颌点云数据法向量计算及显著性概念
1.1 求解单位法向量
关于散乱点云的法向量估计[9]方法, 国内外研究人员提出相关的文献比较多, 同时也提出了多种改进算法, 具体参考表1.

表1 各个法向量估算算法比较
通过对各种算法的分析比较, 本文采用对噪声、尖锐特征以及外点均能很好处理的局部表面拟合的方法来求解点云法向量, 该算法整体计算步骤如下:
1) 构建平面方程

2) 求解约束方程

3) 转化为求解极值问题

1.2 显著性检测概念
显著性检测主要是对二维图像[10]的颜色、特征轮廓、数据信息代表的梯度以及图像纹理等属性进行检测, 由于其具有强大的图像信息提取能力, 因此, 显著性检测被广泛地应用于彩色与灰度图像的分割[11]、自适应图像压缩[11,12]、视频图像特征提取[13]以及新兴的基于内容的图像检索等研究领域.
在三维模型中, 零显著性的区域为一个球面, 本文中我们用各点法向量之间夹角关系来表示三维模型中的显著性, 显著性较高的区域, 其各个点的法向量之间夹角会比较大. 而显著性值较低的区域, 各相邻三维数据点间的法向量夹角会比较小, 如图1和图2,分别展示了特征点、非特征点与相邻点间法向方向与夹角示意图. 因此本文通过引入散乱点云数据与其K邻近点间的法向量夹角值作为显著性度量特征参数,公式如下:
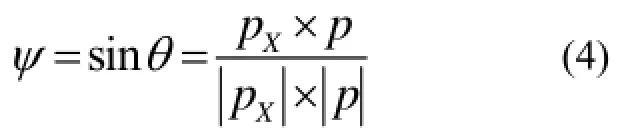

图1 空间数据中特征点与相邻点法向方向和夹角

图2 空间数据中非特征点与相邻点法向方向和夹角
对于三维点集M, 设顶点p的领域N(p,δ), 其中:
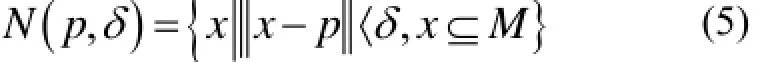
则定义坐标点的高斯平均显著性为:

以上高斯平均显著性计算公式中, 假定高斯滤波器的截止频率为2δ.
1.3 八叉树法原理
八叉树作为区域四叉树向三维空间的推广, 用于描述三维空间的树状数据结构, 通过迭代递归分割模型点云数据空间而实现.
算法流程如下:1)首先读取点云数据,构造数据集的三维空间包围盒,并依此建立点云拓扑关系的基础和模型,并进一步划分为八个子立方体, 同时将其加入到根节点的子节点拓扑结构中. 2)反复迭代第一步, 直到最小子立方体的边长小于或者等于设定的阈值, 到此, 将点云数据集三维空间已经划分为2的幂次方个子立方体(如图3中 (b)和(c)展示的八叉树空间模型建立过程). 如图3中(a)所示, 在八叉树三维模型空间划分流程中, 子立方体拓扑结构的编码与其所在的空间位置紧密相关.
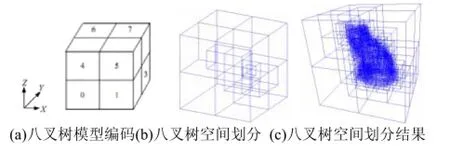
图3 八叉树空间划分模型及划分示意图
2 基于显著性的牙颌点云数据特征提取算法
2.1求解法向量和数据预处理
首先将读取的牙颌点云数据采用局部表面拟合的方法求解法向量求解, 然后进行点云数据的栅格空间划分及模型三维邻域关系的建立.
1) 根据读取的点云数据, 求解每个坐标轴上最大和最小值, 分别为:xmax,xmin,ymax,ymin,zmax,zmin
2) 根据1)计算最小包围盒的大小:

其中N表示所有顶点的个数.
3) 根据步骤2)得到的最小包围盒边长, 计算三个坐标轴上可划分包围盒空间的最大个数:
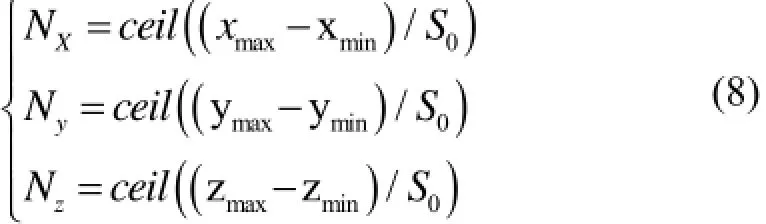
4) 计算每个坐标点在X, Y, Z轴三个坐标的所属包围盒序号:

5) 根据X, Y, Z轴的包围盒序号计算该点所属空间包围盒的BoxID,并存储计算得到的BoxID与该点的ID为式(12):

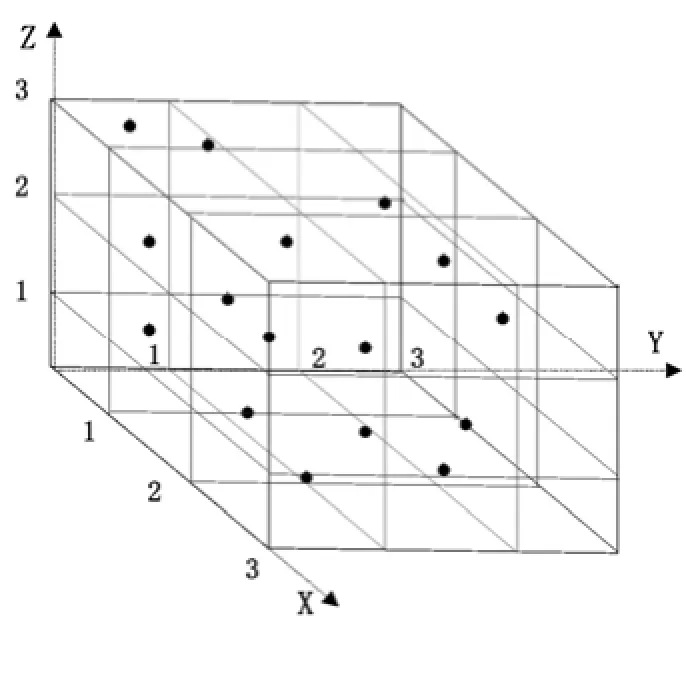
图4 空间包围盒建立示意图
2.2 点云显著性特征值的求解
1) 采用k-d tree算法查找每个点云数据的K邻近点坐标;

2) 利用显著性计算公式(5)求解该点法向量去K邻近点法向夹角值, 并计算对应高斯平均显著性值.

2.3 构建点云八叉树模型
构建八叉树模型首先需要初始化八叉树的根节点, 然后计算出八叉树细分的最小节点长度为

和初始化八叉树最小的菱长为

根据构建的初始八叉树, 按照如下的细分准则对树进行划分: 初始设置一个参数ξ, 计算显著性变化的标准偏差为:
若δ<ξ, 则节点所包含的区域被忽略为一个点;若δ>ξ, 则节点所包含的区域显著性特征值大, 需要细分. 上述两个细分准则能够根据某块固定大小的区域内显著性的方差而去确定是否继续细分. 算法流程图如图5 所示.
3 牙颌点云显著性特征提取算法效果分析
如图6所示为单颗牙齿点云数据及特征提取效果图, 图中的红色点为采用显著性方法提取的特征点,蓝色点为非特征点. 从图6(b)的法向量结果来看, 提取出来的显著性特征值有很多都不是单颗牙齿中实际的显著性特征值, 其对于显著特征值提取的准确率很低, 但是从图6(c)的提取效果图来看, 对于单颗牙齿的边缘特征值都已经成功提取出来, 并且并没有提取出多余的非特征值点. 对于图7的完整牙颌点云显著性特征值的提取效果来看, 法向量求解提取出来的特征值有很多都是非显著性特征值, 而图7(c)中采用显著性特征提出的较多都是完整牙颌点云数据的显著性特征值. 从图8中的完整牙颌点云数据特征提取局部放大效果对比图中也可以看出显著性特征提取出来的特征值更加准确可靠.

图5 算法总流程图

图6 单颗牙齿点云数据及特征提取效果
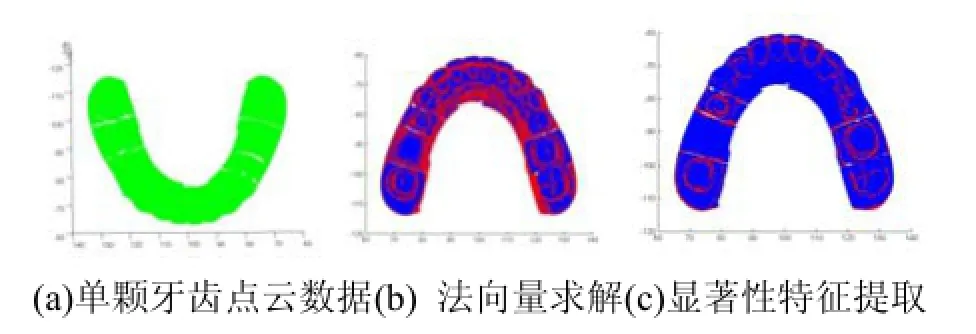
图7 完整牙颌点云显著性特征提取效果

图8 完整牙颌点云特征提取局部放大效果对比图
如图9所示, 是对于三颗牙齿点云数据提取效果对比图, (b)是针对显著性特征提取出来的效果图, 其中红色点基本都是分布在三颗牙齿的边缘位置和轮廓较明显的位置, (c)是通过高斯曲率特征提取的特征值效果图, 图中的红色点较少, 对于明显的特征位置都未提取出来, 所以其提取特征的效果很差.

图9 三颗牙齿点云特征提取效果对比图
为了验证此基于显著性特征提取方法的实用性,利用斯坦福的开放数据(大象点云数据、兔子点云数据、马点云数据)进行试验, 其运行测试效果图如图10、11、12所示, 从提取出来的实验结果图中可以看出, 每幅点云数据中的边缘轮廓、图像纹理等显著性特征都得到了较好的提取.

图10 大象点云显著性特征提取效果

图11 兔子点云显著性特征提取效果

图12 马点云显著性特征提取局部放大效果
如表1所示, 通过采用颌部分缺失数据和完整牙颌数据, 单颗牙齿数据、三颗牙齿数据, 以及斯坦福大学开放的点云数据做进一步测试, 同时还通过与该点云数据的平均曲率特征提取结果比较, 可以明显看出本文算法能够对各种数据的轮廓特征、图像纹理进行有效提取, 并且其时间效率是基于曲率特征提取算法的10%左右.

表1 特征提取算法时间对比分析
4 结语
本文提出一种新的基于显著性牙颌点云特征提取的方法, 该方法利用法向量作为衡量三维点云模型显著性特征的标准, 直接对点云数据进行显著性特征的提取. 通过基础性研究分析, 使用数据点单位法向量与K邻近点的单位法向量的点积均值构建高斯平均显著性参量, 替代以曲率作为该点所在三维模型局部曲面的弯曲程度或者轮廓是否明显的数值表示, 避免了曲率估算过程中引起的较高时间复杂度, 同时利用采集的单颗牙齿、三颗牙齿以及牙颌部分缺失数据和完整牙颌数据进行验证分析, 利用斯坦福大学开放点云数据做进一步测试, 并和曲率特征提取等算法进行对比, 均取得较好效果. 算法不仅保留了对点云细节特征保持方面的优势, 而且在时间效率上得到了提高.
1 Lee KH, Woo H, Suk T. Point data reduction using 3D girds. The International Journal of Advanced Manufacturing Technology, 2001: 201–210.
2 Dyn N, Floater MS, Iske A. Adaptive thinning for bivariate scattered data. Journal of Computationaland Applied Mathematics, 2002.
3 洪军,丁玉成,曹亮,等.逆向工程中的测量数据精简技术研究.西安交通大学学报,2004,38(7):661–664.
4 Song H, Feng HY. A global clustering approach to point cloud simplification with a specified data reduction ratio. Computer-Aided Design, 2008: 281–292.
5 史宝全,梁晋,张晓强,等.特征保持的点云精简技术研究.西安交通大学学报,2010,44(11):37–40.
6 黄文明,肖朝霞.保留边界的点云简化方法.计算机应用, 2010,30(2):348.
7 张欣,秦茂玲,谢堂龙.基于特征保持的三角形折叠网格简化算法.计算机技术与发展,2012,22(1):1–6.
8 Dyn N, Iske A, Wendland H. Meshfree thinning of 3D point clouds. Foundations of Computational Mathematics, 2008, 409–425.
9 李宝,程志.三维点云法向量估计综述.计算机工程与应用,2010,46(23):1–6.
10 Goferman S, Zelnik-Manor L, Tal A. Context-aware saliency detection. IEEE Trans. on Pattern Analysis and Machine Intelligence, 2012, 1915–1926.
11 Perazzi F, Krahenbuhl P, Pritch Y, et al. Saliency filters: Contrast based filtering for salient region detection. 2012 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). IEEE. 733–740.
12 Achanta R, Hemami S, Estrada F, et al. Frequency-tuned salient region detection. IEEE Conference on Computer Vision and Pattern Recognition, 2009. IEEE. 1597–1604.
13 Cheng MM, Zhang GX, Mitra NJ, et al. Global contrast based salient region detection. 2011 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). IEEE. 2011. 409–416.
Significant Feature Extraction for the Dental Point Cloud Data
CHEN Ling-Ling1,2, YANG Ling1,2, QIAO Zhou-San1, CHEN Wen-Le1,212
(College of Electronic Engineering, Chengdu University of Information Technology, Chengdu 610225, China) (Key Laboratory of Atmospheric Sounding of CMA, Chengdu 610225, China)
With the development of laser scanning measurement technology, the detailed information about the surface point cloud data of the geometric model is more abundant due to the more efficient data detection accuracy, make it more precise to show the surface features of objects. However, the corresponding technical challenges may appear at the same time because of such a large amount of point cloud data, which can be used in the computer file storage, data post-processing and software visualization inconveniently and inefficiently. A new algorithm is introduced in this paper. Firstly, we make a space division for point cloud data and establish the domain relationship using the grid method. Secondly, we estimate the point cloud normal vector by means of local surface fitting. Thirdly, we find out the significant value of the coordinate points using the point cloud K field method. Finally, we achieve the point cloud octree according to the significant value. In a word, this algorithm realizes the goal that the significant features of the point cloud can be extracted and the amount of the point cloud data can be simplified. Not only does it retain the advantages of the detail characteristics of the point cloud, but also make it more effective.
point cloud data; visualization; significance feature; 3D registration; grid reconstruction
2016-04-29;收到修改稿时间:2016-07-14
10.15888/j.cnki.csa.005625

