基于102F实测热红外光谱的富硅类岩石SiO2含量定量反演
杜锦锦1 ,2 ,王俊虎2 ,郎朋林3
(1.中国地质大学(北京),北京100083;2.核工业北京地质研究院,北京100029;3.内蒙古山金地质矿产勘查有限公司,内蒙古赤峰024005)
基于102F实测热红外光谱的富硅类岩石SiO2含量定量反演
杜锦锦1 ,2 ,王俊虎2 ,郎朋林3
(1.中国地质大学(北京),北京100083;2.核工业北京地质研究院,北京100029;3.内蒙古山金地质矿产勘查有限公司,内蒙古赤峰024005)
铀多金属矿床的形成与硅化有着密切关系,石英脉也常作为重要的找矿标志,因此,快速识别硅化和石英脉等富硅类岩石(SiO2>70%)对矿产勘查具有重要的指导意义。为实现岩石SiO2含量的快速估算,基于102F实测热红外光谱和化学定量分析进行SiO2含量定量反演,构建了3种反演模型。根据拟合优度最大法和进一步的实验验证,针对102F实测热红外光谱,确定了一种最优反演模型。研究结果为基于航空热红外影像快速识别富硅岩类岩石及其SiO2含量定量估算提供了技术支撑,具有重要的应用价值。
发射光谱;富硅类岩石;SiO2含量;定量反演
热红外波段(8.00~14.00 μm)在对地成像上具有独到优势,不仅可识别硅酸盐、硫酸盐、碳酸盐、磷酸盐、氢氧化物等造岩矿物,更可识别可见-短波红外不能识别的石英等矿物。在自然界中,矿石中常有石英脉石伴生,硅化亦是铀多金属矿产出的重要找矿标志。因此,岩石SiO2含量的定量反演可以快速识别硅化、石英脉(SiO2>70%)等富硅岩类,对矿产勘查具有重要的指导意义。
国内外学者大多基于ASTER等卫星数据或标准光谱库对地表SiO2含量的反演开展基础性研究,并取得一系列成果。Hunt和Salisbury研究发现岩浆岩的发射率光谱特征与SiO2含量具有显著的相关性[1-2];Ninomiya等和闫柏琨等基于ASTER卫星数据开展SiO2含量定量反演,提出了可以定性表征SiO2含量的光谱指数,其研究结果在实际中得到验证[3-5];闫柏琨等和杨长保等以各类光谱库为数据源,对岩石中矿物的成分和含量与发射率光谱特征的相关性进行研究,并建立回归模型,对特定地区或特定岩类进行SiO2含量定量反演[6-8]。利用卫星数据进行SiO2含量定量反演,较低的分辨率限制了反演精度;而利用标准光谱库进行SiO2含量反演比较理想化,不符合野外实际情况。
杨杭等[9]根据野外实测岩浆岩类发射光谱,定义SiO2光谱指数并构建了SiO2含量定量反演的模型,其模型在理论上证实了可行性。但其下行辐射数据未采用金板实测,岩石化学定量分析也仅是X荧光分析仪实测,数据精度偏低,影响了最终反演模型的构建。因此,本文基于102F实测发射光谱和SiO2含量室内化学分析定量结果反演富硅类岩石SiO2含量,并基于实测化学分析数据验证模型反演精度,保证反演模型的精度和实用性。研究旨在为基于航空/航天热红外数据大范围快速识别富硅类岩石奠定基础。
1 实验数据的获取
1.1 岩石发射率光谱测量
野外共采集34个岩石样本,岩性包括硅质卵砾、石英脉岩、硬砂岩、构造角砾岩及硅化蚀变岩等。发射率测量采用美国D&P Instruments公司生产的便携式傅立叶变换热红外光谱仪(102F型现场及工业用FT-IR光谱仪),又称微FTIR光谱仪。与其它热红外光谱仪相比,102F光谱仪采用发射式接收,对测量环境要求较低,在实验过程中不需要使用其他光源的照射,被测样品发出的红外光经由望远镜进入光谱仪,以傅立叶变换的方式进行分光,最后被探测器接收。而且,102F光谱仪的使用简化了测量过程和样品的制备,可以直接对任意形状的样品进行测量。该仪器可以用来测量辐射亮度和发射率等数据,仪器具体的技术指标如表1所示。

表1102 F光谱仪技术参数表Table 1The technical parameter of 102F spectrometer
为了抑制环境噪声的影响,测量时采用加温箱对样品进行均匀加热,保证样品温度与环境温度保持在一定的温差范围,利用T-730系列专业测温仪对样品表面温度进行多次测量,取其平均值作为样品温度,测温精度±0.1℃。
具体测量过程为直接采集冷黑体、热黑体数据、大气下行辐射数据、样品热辐射数据,基于样品温度,用手动普朗克拟合方式对所测得的发射率进行拟合,得到样品的发射率曲线。
1.2 岩石样品SiO2含量化学分析
为了进行SiO2含量的定量反演,室内利用AB-104L,PW2404 X射线荧光光谱仪和电子天平对岩石样品进行了Si、Al、Fe、Mg、Ca等主量元素及烧失量的重量百分数分析。本文选取实验分析数据去除烧失量(LOI)后硅含量不小于65%的样品组成此次试验的样本集。
2 富硅类岩石发射光谱诊断特征分析
2.1 JHU数字标准光谱库的石英发射光谱诊断特征分析
首先对JHU光谱库中不同粒径石英的发射光谱(图1)进行研究。结果表明,在8.00~9.70 μm区间内有2个强的残余辐射谱带和1个发射峰,残余辐射谱带位于8.23 μm左右和9.21 μm左右,发射峰位于8.63 μm左右;在12.25~13.20 μm区间内有2个弱的残余辐射谱带和1个弱的发射峰,弱的残余辐射谱带位于12.50 μm左右和12.81 μm左右,弱发射峰位于12.62 μm左右。不同粒径石英的发射峰的位置始终位于8.63 μm左右和12.62 μm左右,石英粒度、含量的不同则影响其残余辐射谱带的深度及中心波长的位置。标准石英样品发射光谱诊断特征的建立为富硅类岩石的定性识别和SiO2含量的定量反演奠定了基础。

图1 JHU光谱库不同粒径石英样品发射率光谱曲线图(据JHU光谱库)Fig.1 The quartz's emissivity curves of different grain diameter from spectrum database of JHU(Based on spectrum database of JHU)
2.2 基于102F实测富硅类岩石样品发射光谱诊断特征分析
选取19种不同富硅类岩石发射光谱特征(图2)进行分析,得出实测富硅类岩石发射光谱与JHU标准光谱库中石英光谱具有相同的诊断特征,仅在其残余辐射谱带的深度、宽度及中心波长位置略有差异,因此,可以断定所采集的岩石样品确为富硅类岩石样品。

图2102 F光谱仪实测富硅类岩石的发射率光谱曲线图Fig.2The measured emissivity curves of silicon rich rocks by 102F spectrograph
根据JHU标准光谱库中石英(固体样品)和实测富硅类岩石的发射光谱特征分析可以得出,富硅类岩石的SiO2含量不同,其残余辐射谱带吸收深度不同,因此可以根据发射率光谱构建SiO2含量定量反演模型。虽然某些岩石样品的最大发射率大于1,不符合基尔霍夫(Kirchhoff)定律,但利用发射率比值建立SiO2光谱指数,该类数据仍可以利用。
3 富硅类岩石SiO2 含量定量反演
3.1 基本思路
将19个岩石样品分成两组,第1组13个作为试验样本,采用逐步回归法建立回归模型;第2组6个作为测试样本,评价回归模型的精度。为验证反演模型的有效性和实用性,增加了硅含量低的样品进行模型精度评价。具体反演思路为选取石英发射光谱诊断波长,利用中心波长发射率的相对比值构建表征岩石样品SiO2含量的SiO2光谱指数,采用拟合优度(R2)最大法建立SiO2含量和SiO2光谱指数的回归模型,根据回归模型反演出测试样本集的SiO2含量,并基于数据统计和实验分析数据对反演模型的精度进行评价。
3.2 表征SiO2含量的光谱指数构建和诊断波长选取
为减少测量环境、温度等对反演模型的影响,基于实测石英热红外发射光谱诊断波长的相对比值,建立可以表征岩石样品SiO2含量的SiO2光谱指数(εi/εi+1)(εi为特定波段的发射率,i=1,2,…,8)。石英的发射光谱在8.00~9.70 μm区间,12.25~13.2 μm区间有4个残余辐射谱带和2个发射峰。在上述2个诊断特征波长区间内选取8个波段(b1=8.007 64 μm,b2=8.224 7 μm;b3=8.631 5 μm;b4=9.212 5 μm;b5=12.293 3 μm;b6=12.513 4 μm;b7=12.626 5 μm;b8=12.811 7 μm)发射率(εi,i=1,2,…,8),即四个发射峰的最大发射率和4个残余辐射谱带中心波长的最小发射率为诊断波长(表2)。
3.3 SiO2含量定量反演模型构建
3.3.1 SiO2含量和SiO2光谱指数相关性分析

表2 岩石中SiO2含量及光谱指数Table 2The chemically determined SiO2content and εi/εi+1

表3 SiO2含量和εi/εi+1之间的相关性(据SPSS 19.0)Table 3The correlation between chemically determined SiO2content and εi/εi+1(By SPSS 19.0)
根据统计学原理,运用社会科学统计软件包(Statistical Package for the Social Science,SPSS)软件对数据进行处理运算。构建SiO2含量定量反演模型,需明确SiO2化学分析含量和表征SiO2含量的SiO2光谱指数之间是否具有相关性。首先进行试验样本集的SiO2化学分析含量和表征SiO2含量的SiO2光谱指数(表3)之间的相关性分析。表中“Pearson相关性”表示变量之间是否有线性相关关系,其数值介于-1与+1之间,如果|ρ|≈0,表明两个变量没有线性相关关系。如果|ρ|≈1,则表示两个变量完全直线相关。线性相关的方向通过相关系数的符号来表示,“+”号表示正相关,“-”表示负相关。表中“显著性(双侧)”是估计总体参数落在某一区间内,可能犯错误的概率,用α表示,则1-α为置信度或置信水平,表明区间估计的可靠性。显著性是对差异的程度而言的,程度不同说明引起变动的原因也有不同:一类是条件差异,一类是随机差异。它是在进行假设检验时事先确定一个可允许的作为判断界限的小概率标准。即假设检验运用了小概率原理,事先确定作为判断的界限,即允许的小概率的标准,称为显著性水平。一般要求显著性水平在0.05以下,因为5%可以被认为是小概率事件,因此本文采用的显著性参数为α=0.05。N为参与分析的样品个数。
从表3可得出岩石样品SiO2含量和SiO2光谱指数在α=0.01水平(双侧)上显著相关,小于α=0.05。SiO2含量和SiO2光谱指数(εi/ εi+1)之间的Pearson相关系数的绝对值都较大,具有线性相关关系,可以进行回归分析。为了确定它们之间的相关关系,利用SiO2化学分析含量和SiO2光谱指数(εi/εi+1)进行线性及二次回归拟合(图3)。
据图3得出利用SiO2化学分析含量与SiO2光谱指数的散点、线性回归及二次回归拟合图,从图中可以看出变量之间具有明显线性关系,其二次回归拟合曲线的拟合优度(R2)均比线性回归的拟合优度(R2)大,SiO2化学分析含量和SiO2光谱指数(ε1/ε2)及SiO2光谱指数(ε7/ε8)的二次拟合优度R2>0.8,而SiO2化学分析含量和SiO2光谱指数(ε3/ε4)及SiO2光谱指数(ε5/ε6)的二次拟合优度R2<0.8。综合分析得出,可以根据SiO2光谱指数(ε1/ε2和ε7/ε8)构建一元二次回归模型,并且利用所有SiO2光谱指数构建多元二次回归模型。
3.3.2 模型回归结果及评价
根据以上分析,运用SPSS 19.0软件,可在α=0.01水平上剔除不合格变量,采用逐步回归法,得到3种较优的二次回归方程(表4)。
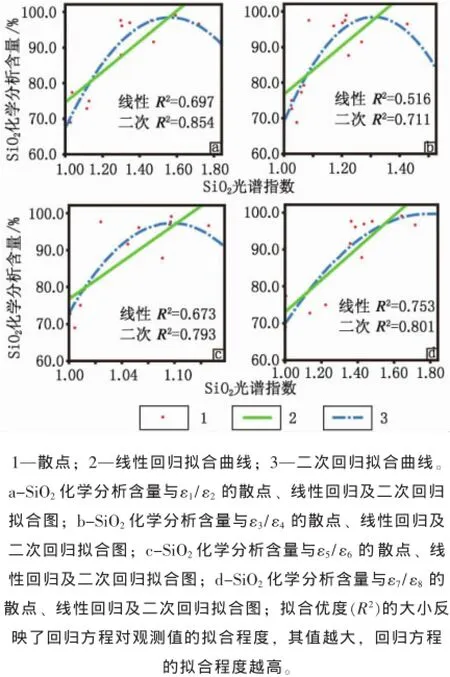
图3 SiO2化学分析含量与SiO2光谱指数的散点、线性回归及二次回归拟合图Fig.3The scatter diagram,quadratic and cubic regression between chemically determined SiO2content and εi/εi+1

表4 最优二次回归模型Table 4The optical quadratic regression models
从上述3种模型中可以得出,尽管模型2中的SiO2光谱指数(ε7/ε8)与SiO2化学分析含量之间的相关性最大(ρ=0.868),但其回归模型的拟合优度却在3种模型中最小(R2=0.801);模型3是多元二次回归模型,其拟合优度在3种模型中最大(R2=0.876),但其标准估计的误差最大(5.540 7);模型1的SiO2光谱指数(ε1/ε2)的回归模型的拟合优度居中,但其标准估计的误差最小(4.646 7)。根据拟合优度最大法,模型3为最优模型;为了进一步评价其反演精度,本文选取了实测SiO2含量的岩石样品进行精度评价(表5)。总体上看,对于SiO2含量为66.49%的测试样品,所有回归模型的预测值误差大,反演精度较低;对于其余的5个测试样本,3种回归模型的预测误差小,精度高(>90%)。
3种模型相比,模型3(Y^)的拟合优度值(R2)最高,其反演精度略低于其他两个反演模型。模型1(Y1)和模型2(Y4)反演的SiO2含量的误差相对较小,尤其模型1(Y1)对含金石英脉样品反演的SiO2含量为98.375%,模型2(Y4)对含金石英脉样品反演的SiO2含量为98.762%,反演精度都在99%以上,基本和化学分析的SiO2含量(98.35%)一致。综合分析得出,模型1和模型2都可作为SiO2含量定量反演较优模型。

表5 较高SiO2含量样品反演及反演精度Table 5The chemically determined high SiO2content and the output of quadratic regression models for the 102F in the traning data and models'accuracy
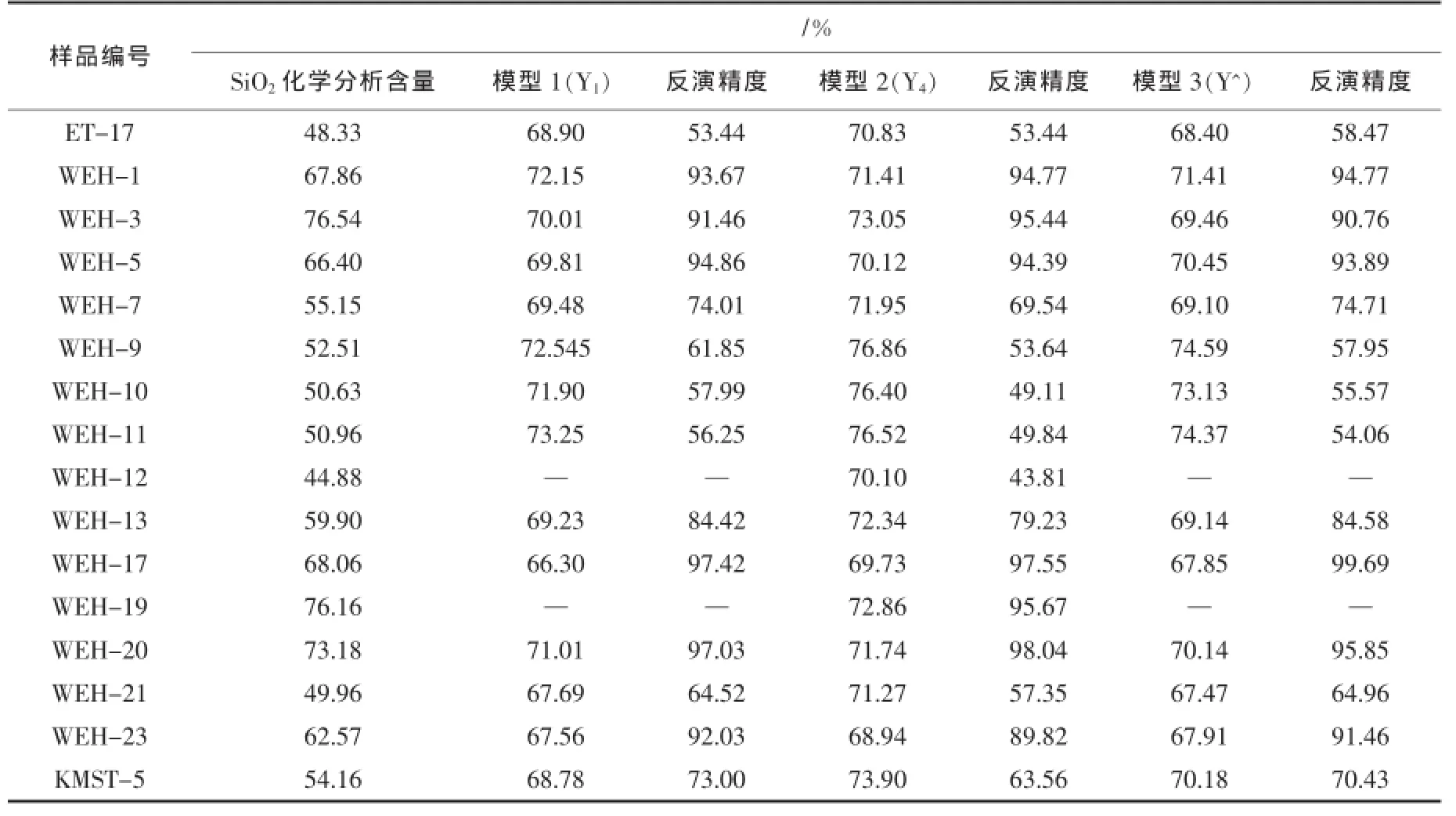
表6 较低SiO2含量样品反演及反演精度Table 6The chemically determined lower SiO2content and the output of the quadratic regression models for the 102F in the traning data and models'accuracy
此外,对SiO2含量低或发射光谱噪声较大的样品进行SiO2含量反演(表6),含量较低或噪声过大时,不能提取所需要的数据,构不成所需的SiO2光谱指数,不能利用相应的模型进行反演。根据分析可知,不论使用何种模型进行反演,SiO2含量较低(SiO2<60%)的岩石样品,其精度较低,约为50%;而SiO2含量较高(SiO2>60%)的岩石样品,其反演精度较高,约为90%。总体而言,利用3种模型的反演结果可以半定量估算富硅类岩石的SiO2含量,但对于贫硅类岩石的SiO2含量的预测还有偏差,需要进一步研究改进。
另外,在热红外短波方向发射光谱噪声较大时,提取发射率数据困难,不利于使用模型1和模型3,但可以用模型2进行反演,SiO2含量较低(SiO2=44.88%)时,反演精度为43.81%;SiO2含量较高(SiO2=76.16%)时,反演精度为95.67%。
4 结论
基于102F热红外光谱仪测量的发射率相对比值建立的SiO2光谱指数(εi/εi+1)和SiO2化学分析含量构建了3种SiO2含量定量反演模型,经过精度评价和综合分析得出了最优SiO2含量反演模型:Y4=-5 475.027+10 331.575X4-4 786.819X42。该模型使用变量少,反演精度高,并且当热红外发射光谱在短波区域出现噪声或被其它矿物发射光谱特征遮盖,不利于提取其SiO2光谱指数时,依旧可以使用。
基于其他数据源(如TASI等)的热红外光谱曲线,其波长不能达到13.50 μm,则可以采用模型1(Y1=-140.870+306.110X1-97.885X12)进行反演,对于富硅类岩石中SiO2含量的反演其反演精度也可达到90%以上。
通过测试样本集检验各个定量反演模型的精度,可以得出:所建模型在SiO2含量较高(SiO2>60%)时,反演精度较高,效果好,证明了该最优反演模型在实际应用的有效性及实用性。研究结果可为基于航空/航天热红外影像快速识别富硅类岩石及SiO2含量定量估算提供技术支撑,具有重要的应用价值。
[1]Hunt G R,Salisbury J W.Mid-Infrared Spectral Behavior of Igneous Rocks[J].Air Force Cambridge ResearchLaboratoryTechnicalReport,1974,AFCRL-TR-74-0625.142.
[2]Salisbury J W,Walter L S,D’Aria D.MidInfrared(2.5 to 13 μm)Spectra of Igneous Rocks[J].US Geal.Surv.Open File Report,1998,88:686.
[3]Yoshiki Ninomiya.Quantitative estimation of SiO2content in igneous rocks using thermal infrared spectral with a neural network approach[J].IEEE Transactionson Geoscience and Remote Sensing,1995,33(3):684-691.
[4]二宫芳树,傅碧宏.帕米尔东北缘ASTER多光谱热红外遥感数据的岩性信息提取[J].新疆地质,2003,21(1):22-28.
[5]闰柏琨,王润生.热红外遥感岩矿波谱机理及信息提取技术方法研究[D].北京:中国地质大学(北京),2006.
[6]闫柏琨,王润生,甘甫平,等.热红外遥感岩矿信息提取研究进展[J].地球科学进展,2005,20(10):1 116-1 126.
[7]闰柏琨,刘圣伟,王润生,等.热红外遥感定量反演地表岩石的SiO2含量[J].地质通报,2006,25(5):639-643.
[8]杨长保,朱群,姜琦刚,等.ASTER热红外遥感地表岩石的二氧化硅含量定量反演[J].地质与勘探,2009,45(6):692-696.
[9]杨杭,张立福,黄照强,等.基于热红外光谱的岩石SiO2含量反演模型研究[J].光谱学与光谱分析,2012,32(6):1 611-1 615.
Quantitative inversion of SiO2contents in silicon rich rocks based on measured 102F thermal infrared spectra
DU Jinjin1,2,WANG Junhu2,LANG Penglin3
(1.China University of Geosciences(Beijing),Beijing 100083,China;2.Beijing Research Institute of Uranium Geology,Beijing 100029,China;3.Inner Mongolia Gold Geology and Mineral Exploration Ltd Co.,Chifeng,Inner Mongolia 024005,China)
Formation of uranium-polymetallic deposits are closely related to silicification,quartz vains arecommonly used as important indexes in mineral prospecting.Hence,the quick discrimination silicon rich rocks such as silication and quartz vains(SiO2>70%)play an important guideline role in mineral prospecting.To estimate SiO2contents in rocks quickly,we have established 3 kinds inverse models which can invert SiO2contents,and chemically determined SiO2contents with measured 102F thermal infrared spectra.According to the degree of and the further validation,the optimal model selected for the data retrieving from 102F spectrometer.The result provides a technical support for fast identification of silicon rich rocks and quantitatively estimation of SiO2contents with aerial thermal infrared image.
emission spectrum;silicon rich rocks;SiO2contents;quantitative inversion
P575.4;P595
A
1672-0636(2016)04-0216-07
10.3969/j.issn.1672-0636.2016.04.005
2015-10-22;
2016-03-03
杜锦锦(1990—),女,安徽宿州人,硕士研究生,研究方向:热红外遥感及其在岩石学中的应用。E-mail:DU_Kitty@163.com

