大型集装箱船甲板纵骨节点疲劳寿命预报方法
罗 盼,黄小平,孔小兵
(上海交通大学 高新船舶与深海开发装备协同创新中心,上海 200240)
设计与研究
大型集装箱船甲板纵骨节点疲劳寿命预报方法
罗 盼,黄小平,孔小兵
(上海交通大学 高新船舶与深海开发装备协同创新中心,上海 200240)
针对大型高强度厚钢甲板纵骨结构的疲劳热点,用基于断裂力学的裂纹扩展寿命预报方法进行疲劳寿命评估。直接采用《船体结构疲劳强度指南》中的疲劳载荷计算公式计算纵骨名义应力;结合纵骨节点焊趾处表面裂纹应力强度因子经验计算式和裂纹扩展率单一曲线模型对大型集装箱船甲板纵骨的疲劳寿命进行预报。对集装箱船扁钢型纵骨端部连接节点表面裂纹应力强度因子进行一系列数值计算,结果表明,该应力强度因子与 BS7910中十字接头焊趾处表面裂纹应力强度因子经验公式的计算结果相差很小,该公式可直接用于纵骨端部表面裂纹的应力强度因子计算。对某大型集装箱船甲板典型纵骨节点焊趾处表面裂纹进行疲劳寿命评估,根据不同载荷工况组成不同的载荷谱,讨论疲劳载荷谱对疲劳裂纹扩展的影响。
甲板纵骨;裂纹扩展;应力强度因子;疲劳寿命预报
0 引 言
大型集装箱船具有货舱开口大、方型系数小、剖面变化显著、艏外飘明显和航速高等特点,为减轻其自重,船体结构大量采用高强度钢[1]。大型集装箱船的甲板纵骨都采用高强度钢,且纵骨端部连接节点属于应力集中区域,是疲劳强度校核的重点之一。由于其结构形式简单,因此可采用船级社疲劳强度指南中的简化应力分析方法直接求取其疲劳载荷;与设计波法和谱分析法相比,该方法计算简便、易于操作。大型集装箱船纵骨焊接节点主要可简化为对接接头、T型接头和十字接头 3种焊接连接形式[2](见图1)。目前对接接头和 T型接头的焊趾表面裂纹应力强度因子的计算[3-7]已相当成熟;而关于十字接头的焊趾表面裂纹应力强度因子的计算,虽然BS 7910[4]中给出了具体的计算公式,但其是否适用于大型集装箱船甲板纵骨实际结构的计算有待论证。这里采用三维有限元技术对大型集装箱船甲板纵骨端部节点表面裂纹应力强度因子进行系列数值计算,并将所得结果与BS 7910十字接头焊趾处表面裂纹应力强度因子经验公式的计算结果进行比较,发现两者吻合良好。因此,该公式可直接用于纵骨端部节点表面裂纹的应力强度因子计算。
基于线性累积损伤的S N- 曲线法[8]已被多个船级社采用,如中国船级社编写的《船体结构疲劳强度指南》[9](以下简称《指南》),可直接进行船体纵骨节点的疲劳强度校核。由于纵骨结构相对简单,因此其名义应力可直接采用《指南》中的简化公式计算;采用基于裂纹扩展的方法预报疲劳寿命,既能使疲劳载荷计算变得简便,又能准确预报疲劳寿命,具有很强的实用性和可操作性。该方法有以下特点:
1) 疲劳载荷-名义应力的范围采用《指南》中给出的公式计算;
2) 结构名义应力的范围采用服从二参数的Weibull分布模型计算;
3) 应力强度因子采用BS 7910中十字接头焊趾处表面裂纹应力强度因子经验公式计算;
4) 疲劳寿命采用基于裂纹扩展的单一曲线模型计算。
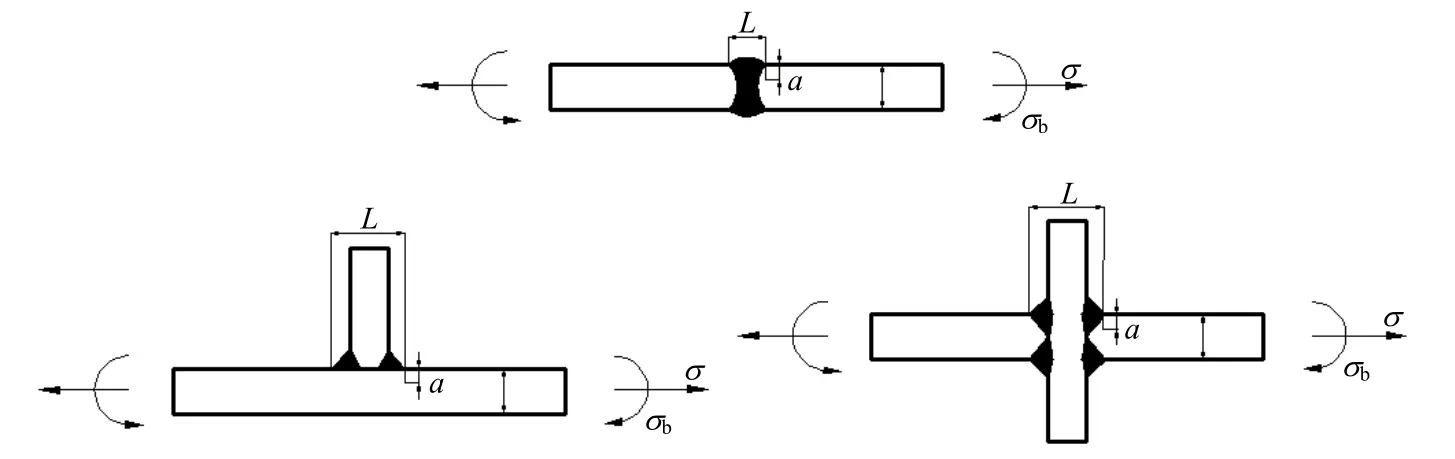
图1 焊接接头结构参数示意
1 疲劳裂纹扩展模型
HUANG[10-12]提出单一曲线模型的概念,该模型是一个由裂纹扩展率单一曲线及相应的等效应力强度因子幅组成的裂纹扩展预报模型,明确了随机载荷作用下裂纹扩展速率曲线采用 0R= 时的裂纹扩展速率曲线,同时分别通过系数RM 和PM 将平均应力及载荷时程效应的影响显示、表达出来;对于BS 7910推荐的三段扩展速率公式,在单一曲线模型中只需一个方程即可很好地表达。其基本表达式为
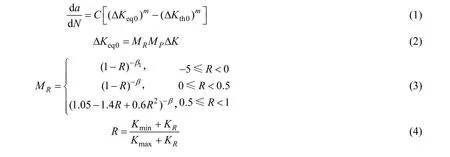

式(1)~式(5)中:Δ Keq0,Δ Kth0分别为等效应力比 R= 0时的等效应力强度因子幅和应力强度因子门槛值;C为Paris系数;m为裂纹扩展指数; MR为载荷比的修正因子; MP为载荷次序的修正因子;a为裂纹半长或裂纹深度,m; aOL为过载时的裂纹半长或裂纹深度,m; ry为裂纹尖端塑性区的大小,m; rOL为过载时裂纹尖端塑性区大小,m;rΔ为由过载-低载引起的塑性区减小量,m;n为载荷效应指数;R为载荷比;β, β1为决定于材料和使用环境的参数; KR为由残余应力引起的应力强度因子,MPa·m1/2; Kmin, Kmax分别为一次应力循环中应力强度因子的最小值和最大值,MPa·m1/2。
2 纵骨名义应力简化计算
2.1 名义应力简化计算原理
名义应力是结构相关截面上计算出的平均应力,仅考虑结构几何形状的影响,不考虑结构不连续和焊缝存在引起的应力集中,其中船体结构宏观几何形状(例如大的开孔、切口等)的影响必须包括在内。名义应力可采用梁理论或粗网格有限元方法求得。由于在计算应力强度因子时需要的是结构的名义应力,即远离裂纹位置处的应力,因此使用简化应力分析方法求解名义应力。
目前世界各主要船级社都有各自的疲劳载荷计算方法,就疲劳载荷简化方法细节和具体规定而言,各船级社采用的方法存在着一定的差别。中国船级社《指南》中给出的疲劳载荷的简化应力计算方法主要包括以下几个方面的内容:
1) 疲劳载荷的计算。疲劳计算工况为目标船典型装载状态与动载荷工况的组合。对于集装箱船,典型装载状态选择满载和压载2种,动载荷工况按《指南》的要求考虑迎浪、随浪和斜浪。由规范公式给出每种计算工况对应10-2的超越概率水平的疲劳载荷。
2) 各应力分量的计算。分析简化应力时考虑船体梁弯曲正应力和纵骨在侧向载荷作用下的弯曲正应力。
3) 名义应力的合成及名义应力范围的求解。根据载荷组合因子,对每种装载工况下的名义应力分量进行合成,得到名义应力,进而求取名义应力的范围。
2.2 甲板纵骨名义应力简化计算
集装箱船的疲劳载荷包括:1) 船体梁载荷,包括静水弯矩和波浪诱导弯矩(垂向弯矩和水平弯矩);2) 舷外海水对舷侧和船底结构的动压力;3) 干散货、液体引起的内部压力及集装箱货物引起的重力。由于集装箱船甲板及其附近的典型纵骨节点只受到船体梁载荷的作用,不受侧向载荷的作用,因此求取典型甲板纵骨节点的疲劳载荷时不必考虑侧向载荷的计算,只需计算船体梁载荷。《指南》中的纵骨简化疲劳计算不考虑波浪扭矩的作用。对甲板纵骨名义应力的计算如下。
2.2.1 中拱及中垂垂向波浪弯矩的计算
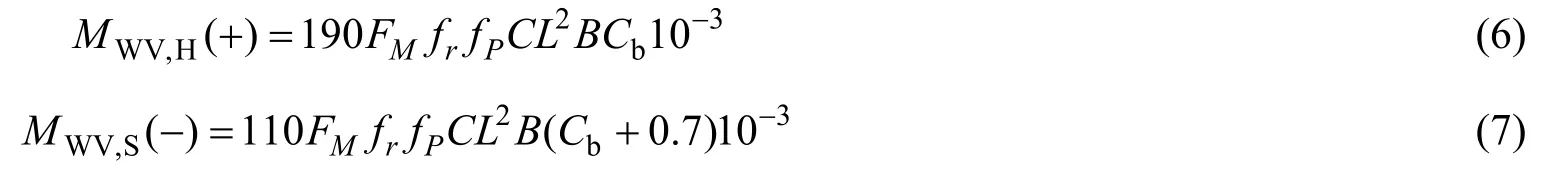
2.2.2 水平波浪弯矩的计算
船体任一横剖面的水平波浪弯矩 MWH的计算式为
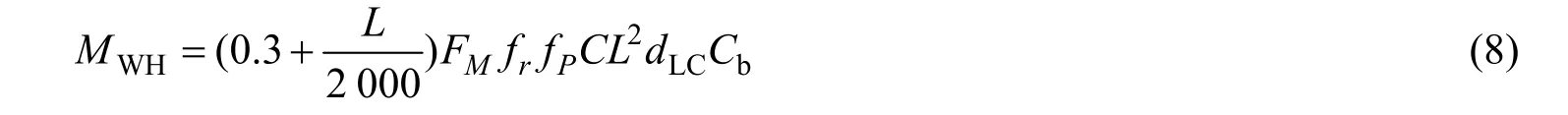
式(6)~式(8)中: FM为分布系数; fr为航区系数; fP为概率水平系数;C为波浪系数;L为船长(m);B为船宽(m); Cb为方形系数; dLC为相应装载工况下的船中吃水(m)。
2.2.3 名义应力分量的计算及合成
《指南》中规定集装箱船疲劳评估装载工况为均匀满载工况和正常压载工况,并定义了与等效设计波相对应的动载荷工况。对于装载工况“(k)”中的载荷工况“ij”,将3种船体梁载荷引起的名义应力进行合成得到其计算公式为
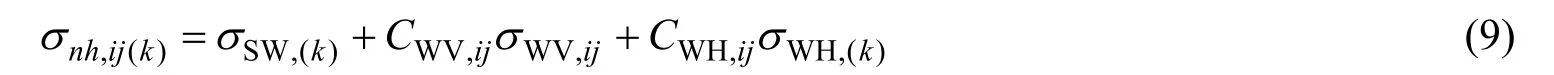
2.2.4 名义应力范围 Δσn的计算
对于装载工况“(k)”中载荷工况“i”的名义应力范围 Δσn,i(k),其计算式为

3 疲劳载荷谱
目前各国已在疲劳强度方面进行大量研究,但长期以来有关船舶结构疲劳强度的研究和疲劳寿命计算涉及因素大多具有不确定性。大量的实船应力测试结果和理论研究结果都表明,由随机波浪外力引起的作用在船体纵向构件上的应力范围 Δσ 的长期分布特征服从两参数的Weibull分布。若能确定Weibull分布的2个参数,则疲劳载荷的长期分布便可得到确定,随机载荷也就可以运用MATLAB产生。两参数的Weibull分布的概率密度函数为
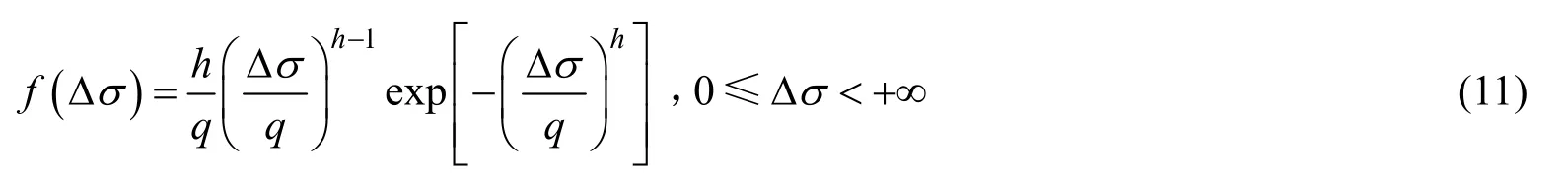
式(11)中:h为形状参数,一般根据结构所处的海洋环境、结构类型、响应特性及构件在整个结构中的位置等因素确定,已有的研究结果表明其取值范围一般为 0.7~1.3[13];q为尺度参数,可用回复期 (n0)内疲劳载荷长期分析得到的对应某个超越概率的应力范围表示。参考《指南》,取 h=1, n0= 102,q可用式(12)计算。

考虑到使用断裂力学的方法,应将名义应力范围作为疲劳载荷。不同的载荷工况对应的名义应力范围Δσ 不同,名义应力范围决定Weibull分布的尺度参数,进而决定疲劳载荷谱。因此,名义应力范围的大小是评判疲劳寿命预报是否准确的关键。
4 扁钢型纵骨端部连接节点应力强度因子计算
扁钢型纵骨端部连接节点在集装箱船的上甲板处,且采用高强度钢厚板结构。选取某大型集装箱船扁钢型甲板纵骨端部为研究对象,扁钢的尺寸为FB900×65,甲板厚65mm,纵骨的间距为850mm。在ANSYS中建立对应局部节点结构含有表面裂纹的体单元有限元模型。与壳单元不同,体单元只有平动自由度而没有转动自由度,因此边界条件只需考虑位移而不用考虑转角,各边的边界条件见表1,纵骨端部结构示意见图2。表面裂纹在扁钢的焊趾处,其中焊趾宽度取10mm,建模完成后施加表1中的边界约束,自由端2施加100MPa的拉压力,三维有限元模型见图3。

表1 纵骨端部模型的边界条件
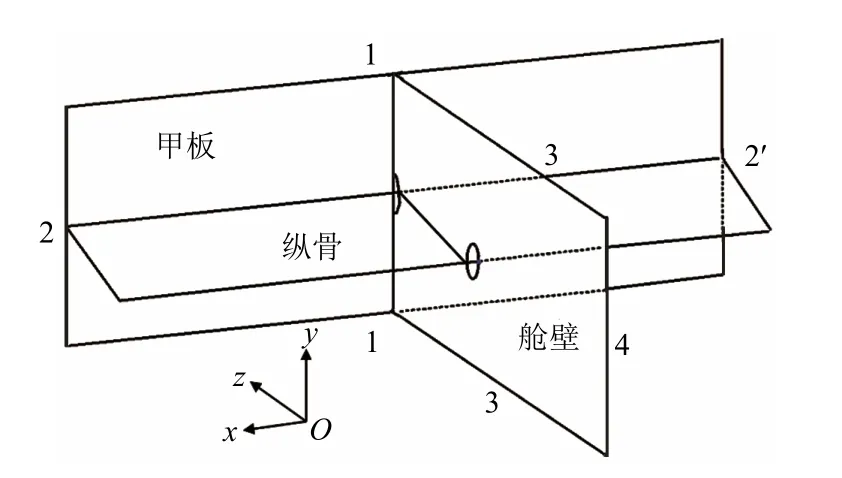
图2 纵骨端部结构示意
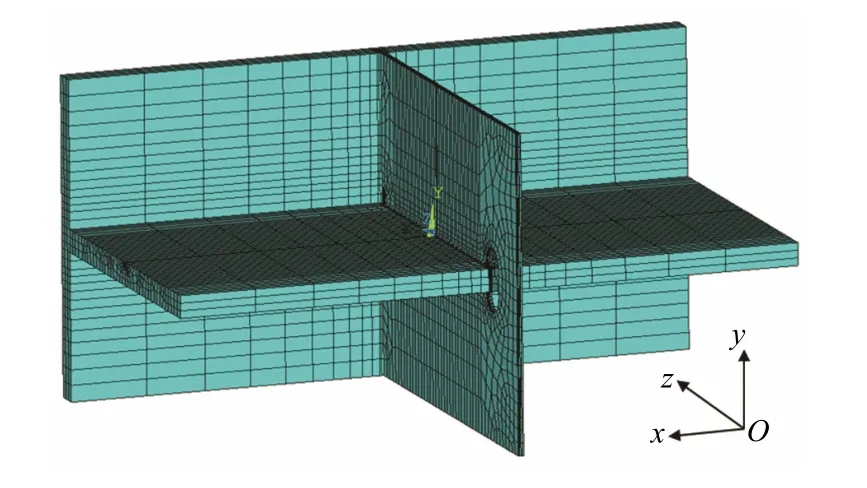
图3 三维有限元模型
计算裂纹深长比为0.3和0.5时表面裂纹在不同尺寸下的应力强度因子,同时根据BS7910的十字接头焊趾处表面裂纹应力强度因子计算式进行计算,并对2种计算方法所得结果进行对比,结果见图4。

图4 应力强度因对比
由图4可知:裂纹深长比为0.3和0.5时,在裂纹最深点利用2种方法得到的结果很接近;在裂纹表面点,2种方法的计算结果也很接近,当裂纹深度较大时有限元计算结果略小,原因是裂纹深度较大时BS7910将应力强度因子修正系数<1的结果都取为1。因此,在计算扁钢型纵骨连接节点表面裂纹应力强度因子修正系数时,可直接采用BS7910的十字接头焊趾处表面裂纹应力强度因子修正系数公式。
5 实例分析
某大型集装箱船总长366m,垂线间长350.5m,设计型宽51.2m,设计型深30.2m,结构吃水15.5m,设计吃水14.0m。该集装箱船上甲板的一根扁钢纵骨高为0.9m,厚度达65mm。船中剖面(FR220)处的扁钢型纵骨端部连接节点焊缝处存在表面裂纹缺陷。校核节点所在横剖面的位置见图5,FR220剖面信息见表2,裂纹所在位置见图6,具体信息见表3。
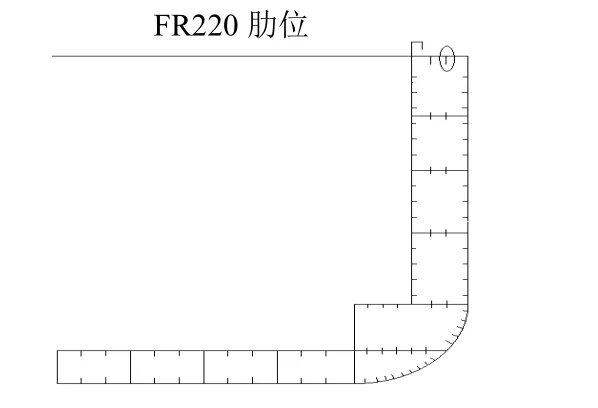
图5 船中剖面(FR220)

图6 裂纹所在位置

表2 FR220剖面信息

表3 剖面FR220(船中)处纵骨端部节点
5.1 疲劳载荷计算
5.1.1 名义应力范围计算
根据前面介绍的简化应力计算编制程序得到所选取的典型纵骨端部节点在均匀满载和正常压载时各工况下的名义应力。表4和表5分别为均匀满载及正常压载工况下的平均名义应力与名义应力范围。由表4和表5可知:由于名义应力范围对应波浪诱导弯矩引起正应力,因此不同载荷工况下的名义应力范围差别比较大;但是,各载荷工况下的平均应力几乎相同,这是因为平均应力是静水弯矩引起的正应力。
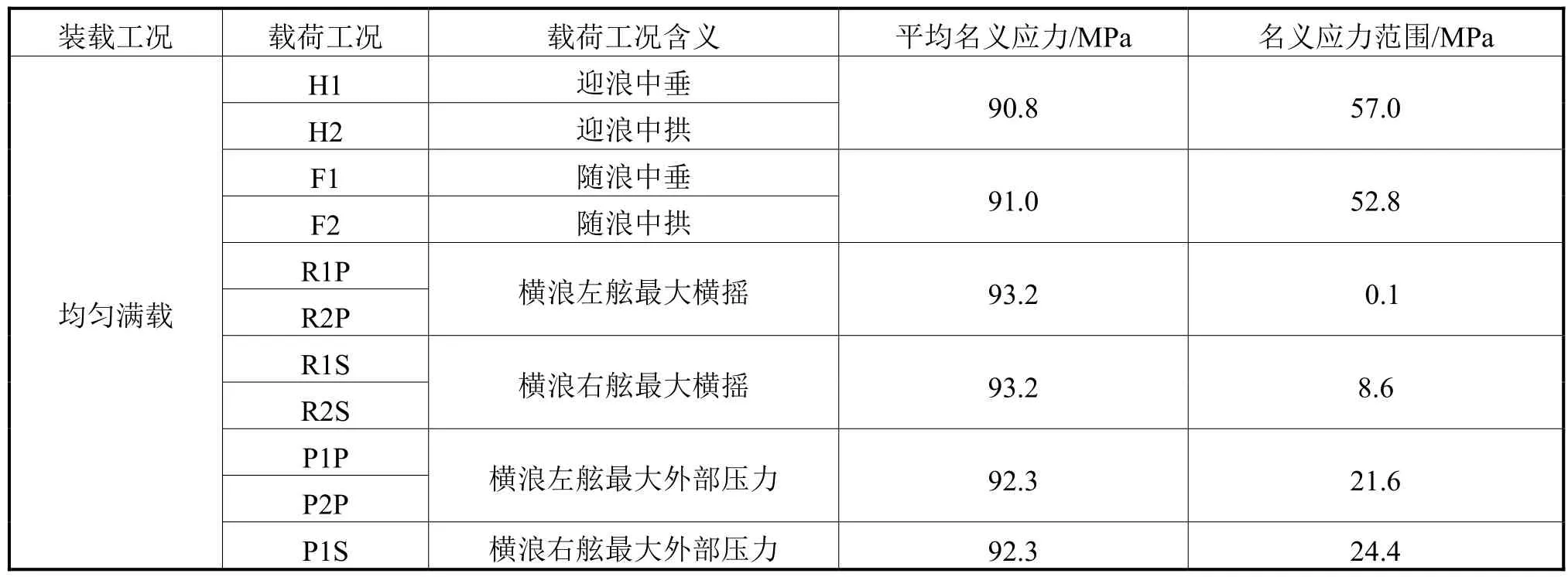
表4 均匀满载工况下的平均名义应力与名义应力范围
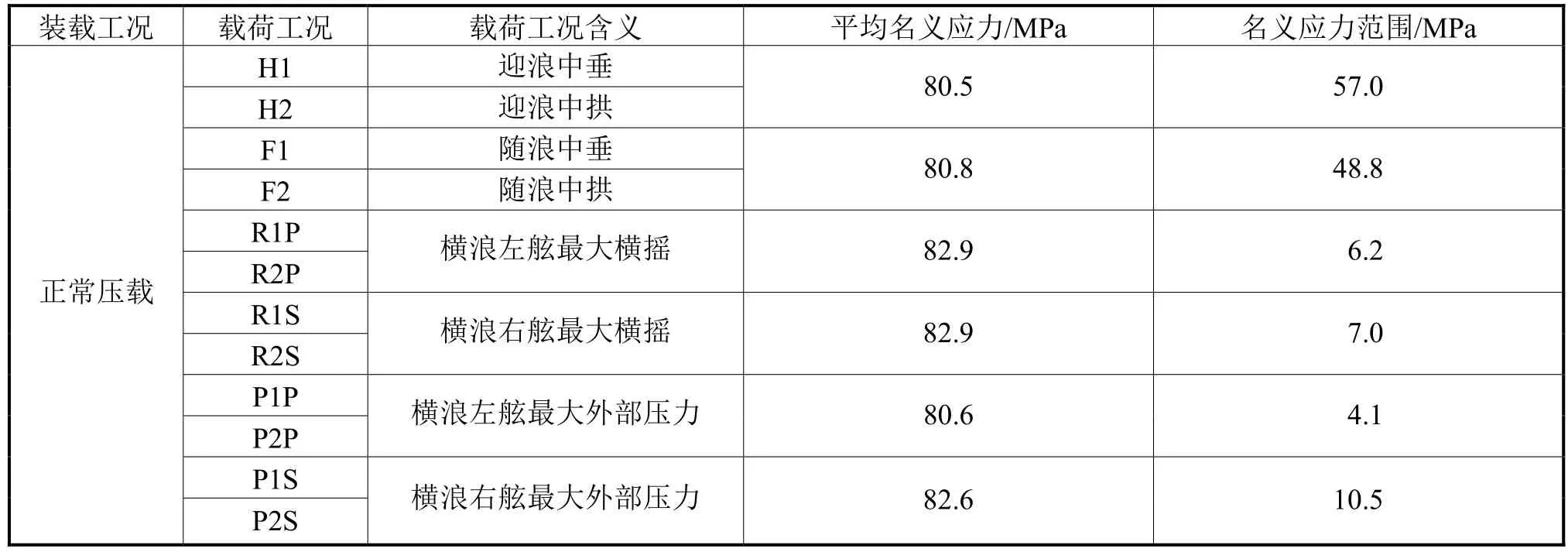
表5 正常压载工况下的平均名义应力与名义应力范围
5.1.2 随机载荷谱的生成
以上得到的名义应力范围对应的超越概率水平为10-2,若按 Weibull分布生成随机载荷谱,则须根据式(12)将其转化为超越概率水平为10-8下的名义应力范围,转化后的结果见表6。使用MATLAB编程,将转化后的名义应力范围 Δσn0按Weibull分布生成一定数量的随机数,每个随机数即为每个循环对应的疲劳载荷应力范围 Δσn,其频率分布见图7,随机载荷片段图见图8。总随机数为6.5×107次,对应的集装箱船设计疲劳寿命为20a。为保守起见,首先校核最极端的情况,即同时考虑均匀满载和正常压载2种装载工况的主导工况,根据集装箱船装载工况的时间分配系数(见表7)确定均匀满载时主导工况对应的随机数为4.96×107次,正常压载时主导工况对应的随机数为1.54×107次。主导工况名义应力范围 Δσn的Weibull分布的概率密度函数为


表6 超越概率水平为10-8下的名义应力范围
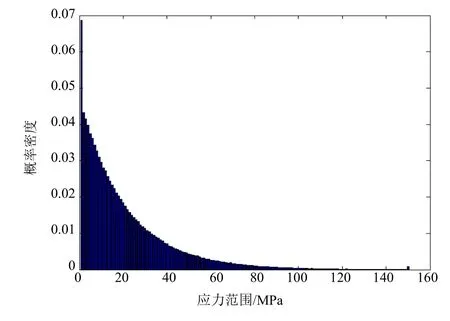
图7 疲劳载荷应力范围频率分布
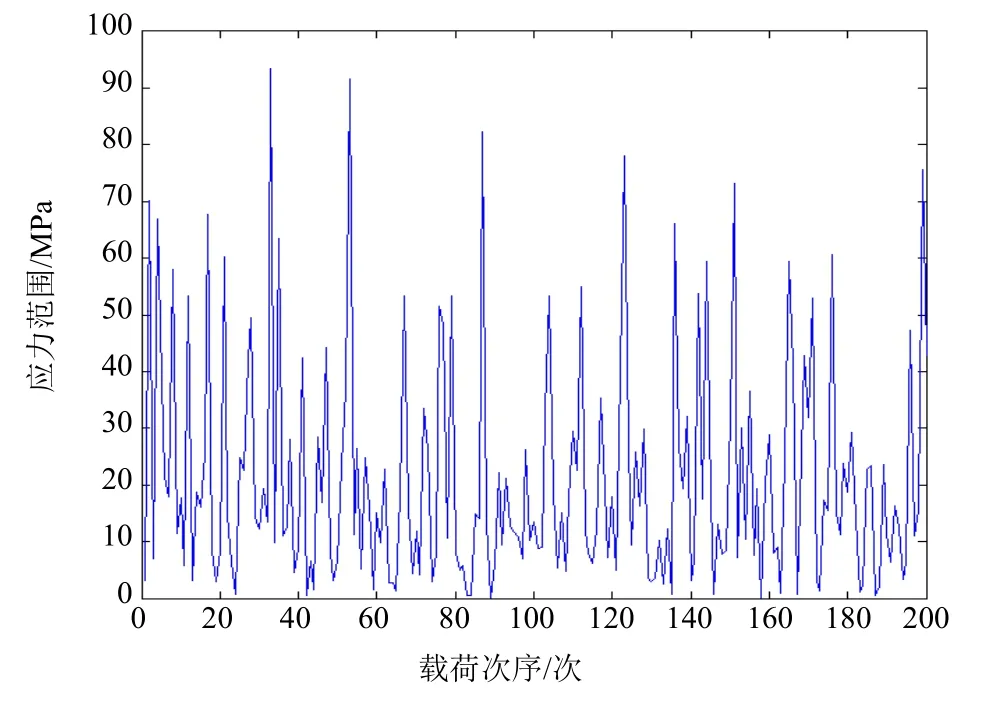
图8 随机载荷片段图

表7 装载工况参数
5.2 裂纹扩展计算及分析
该节点材料为EH40钢,具体材料属性参照国际焊接规范(见表8)。选择以下4种初始裂纹尺寸,固定裂纹深长比a0/ c0= 0.2,深度 a0分别取为0.5mm,1.0mm,1.5mm和2.0mm,使用上文生成的疲劳载荷谱。将该节点简化为十字接头,采用BS7910的十字接头焊趾处表面裂纹应力强度因子经验公式计算应力强度因子,结合单一曲线模型对该节点进行疲劳寿命评估。根据系数 MR和 MP将平均应力及载荷时程效应对疲劳寿命的影响表达出来,其中平均应力包括静水弯矩引起的正应力和残余应力。

表8 EH40钢的基本性能参数
图8和图9分别为裂纹沿深度和长度方向上的裂纹扩展曲线。从图中8和图9可看出,初始裂纹 a0和c0较大时,裂纹扩展速率较大,故当循环次数相同时最终裂纹尺寸较大,或当裂纹穿透板厚时载荷循环次数较少。初始裂纹尺寸的大小对疲劳寿命的影响显著,合理地确定初始裂纹尺寸是分析裂纹扩展的关键。
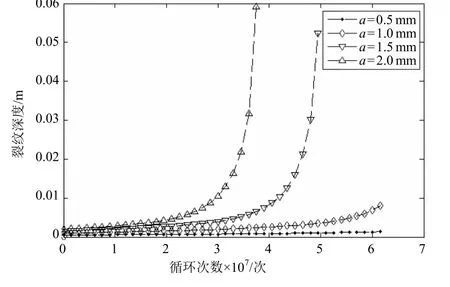
图8 裂纹深度随循环次数的变化
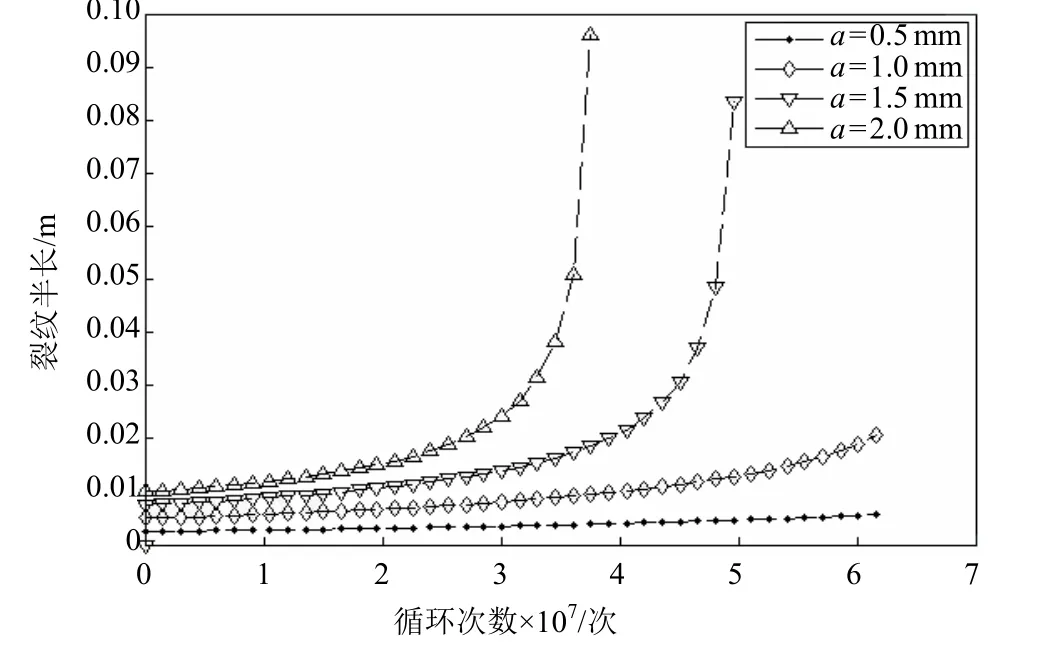
图9 裂纹长度随循环次数的变化
6 不同组合的疲劳载荷谱对裂纹扩展的影响
上述实例计算考虑了最极端的工况,即船舶在寿命期内的均匀满载和正常压载工况均为主导工况。主导工况下的名义应力范围最大,这时预报得到的疲劳寿命最短。若同时考虑2种装载工况下的各6种载荷工况,则这些载荷工况所占疲劳寿命期的比例和组合方式都会影响疲劳载荷谱。因此,有必要对不同情况的疲劳载荷进行模拟,探究疲劳载荷谱对疲劳寿命的影响。由于仅根据各工况的比例和组合方式难以真实地模拟实际载荷,同时限于组合种类繁多和篇幅有限,仅作为一种方法讨论其中几种假设情况。考虑装载工况的时间分配系数,假设满载时6种工况中迎浪和随浪2种工况共占一半且平均分配,横浪左舷最大横摇、横浪右舷最大横摇、横浪左舷最大外部压力和横浪右舷最大外部压力4种工况共占剩余的一半且平均分配;载荷工况的分配情况参照满载工况,具体见表9。此外,列出5种排列方式,具体见表10。
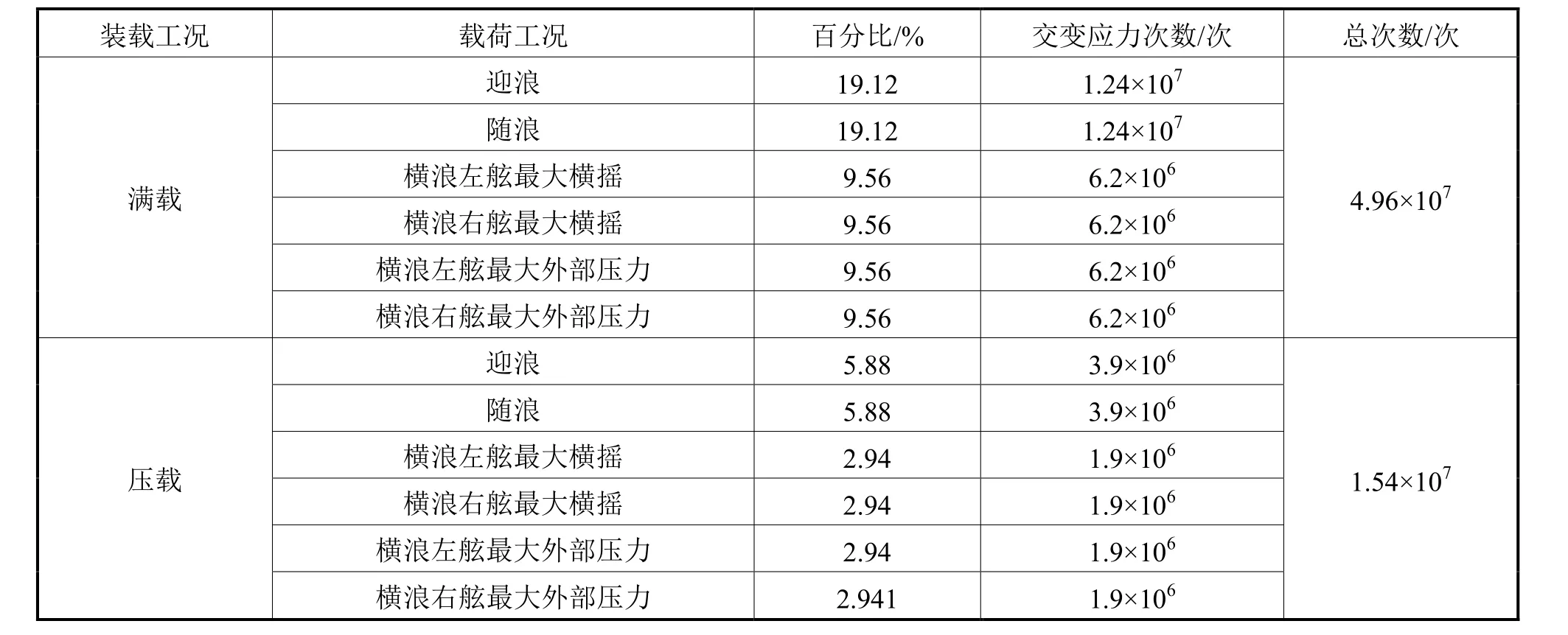
表9 载荷工况的分配

表10 载荷工况的排列方式
各工况对应的名义应力范围按照上述实例分析取值,根据以上 5种排列方式生成的疲劳载荷谱见图10~图14,将生成的5种疲劳载荷谱加载到前述纵骨算例中,初始裂纹为表面裂纹,深度 a= 2mm,深长比 a/ c= 0.2。

图10 疲劳载荷谱分布1

图11 疲劳载荷谱分布2
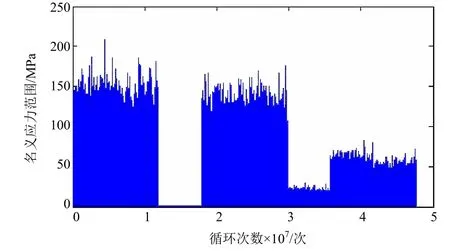
图12 疲劳载荷谱分布3
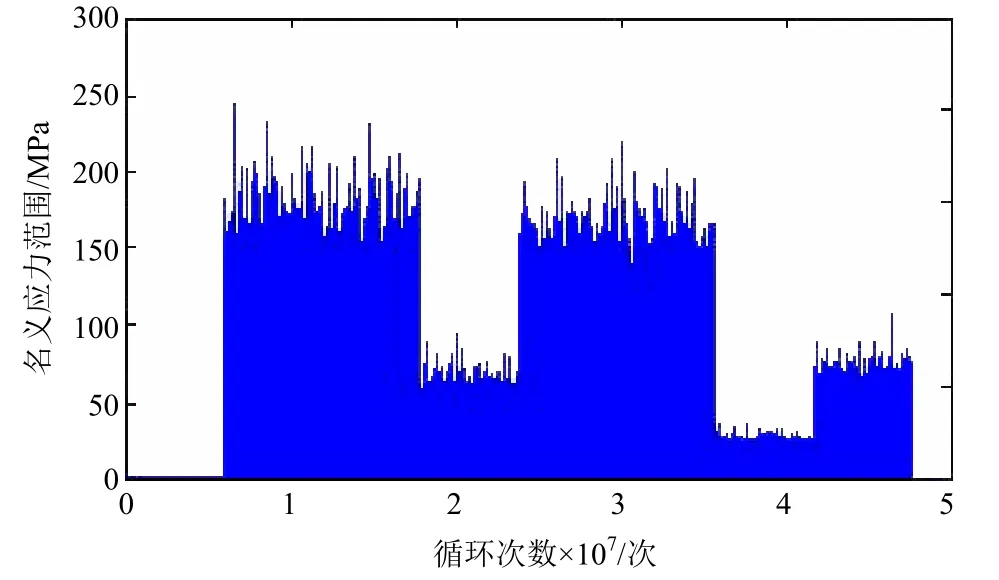
图13 疲劳载荷谱分布4
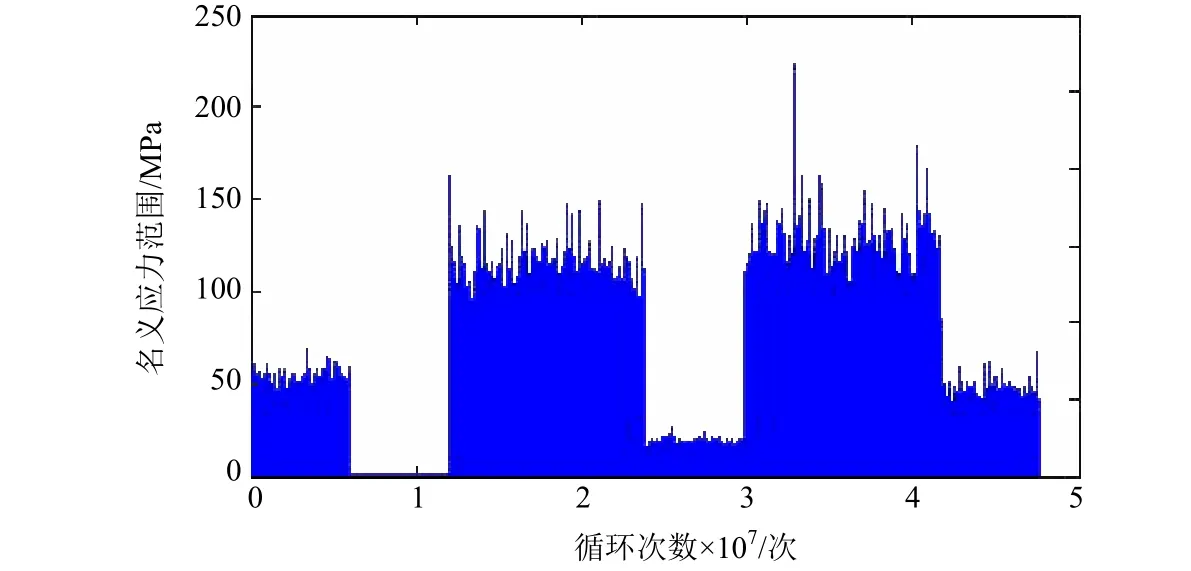
图14 疲劳载荷谱分布5
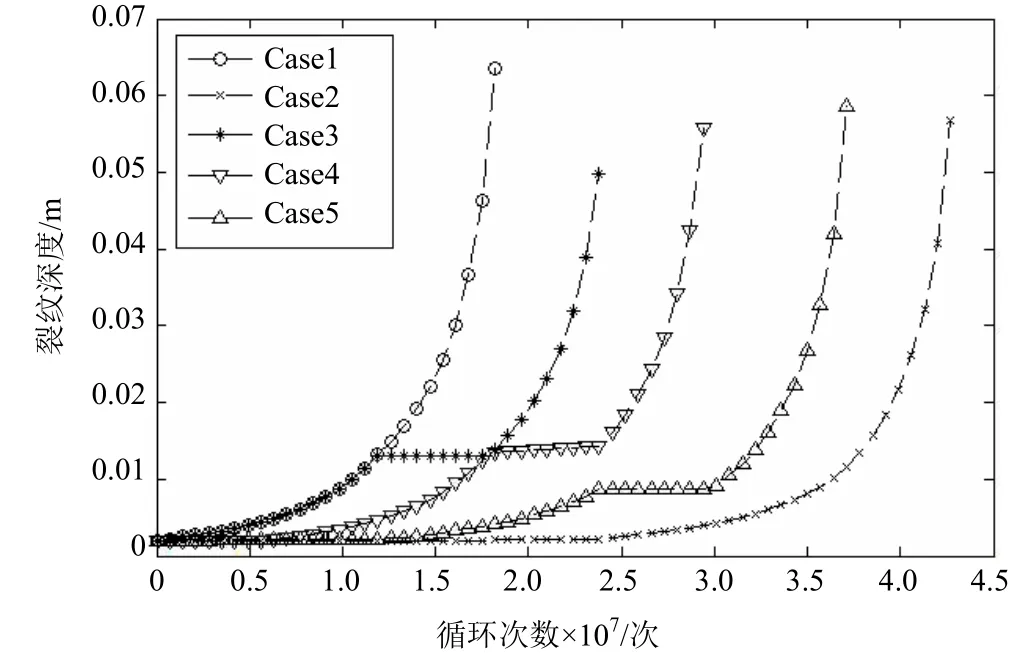
图15 裂纹深度方向的扩展曲线
将各工况载荷谱块的5种组合作为载荷谱,得到的裂纹扩展曲线深度方向和长度方向见图15及图16。
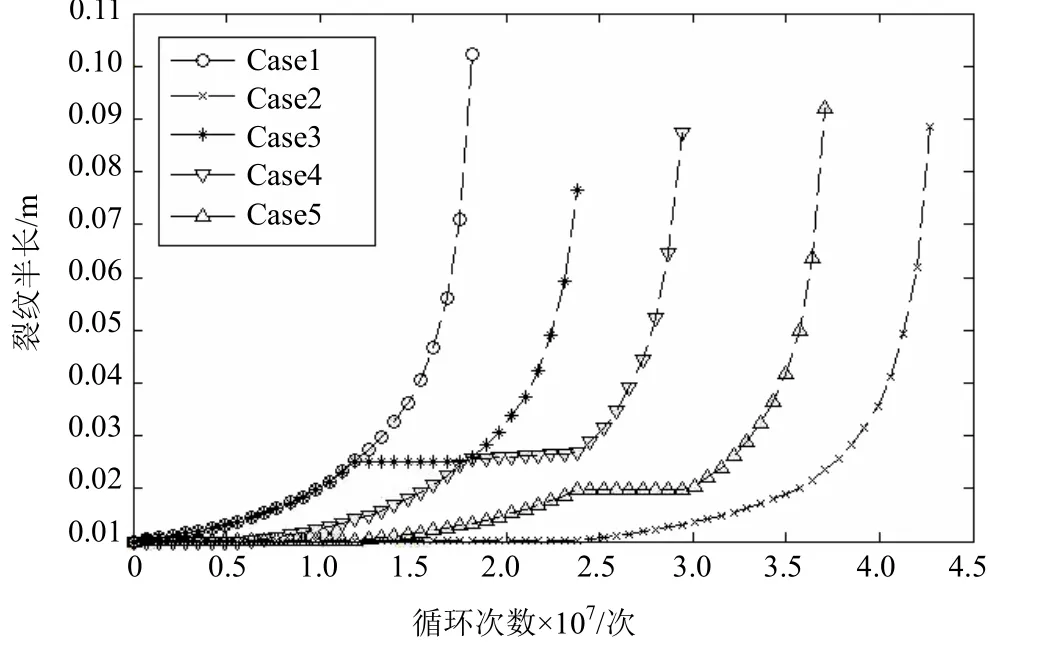
图16 裂纹长度方向的扩展曲线
由以上结果可知,加载 5种载荷谱,结构失效时的载荷循环次数均不同,大致分布区间为1.7×107~4.3×107。当疲劳载荷谱是由大到小的载荷谱块排列组合而成时(如Case1),与其他排列组合的载荷谱相比,裂纹会最早迅速扩展,直至穿透板厚,结构失效时对应的载荷循环次数也最小。当疲劳载荷谱是由小到大的载荷谱块排列组合而成时(如Case2),裂纹缓慢扩展或不扩展的时间最长,结构失效时对应的载荷加载次数也最大。当疲劳载荷谱是由大小交替的载荷谱块排列组合而成时(如 Case3,Case4和Case5),裂纹扩展的速率和结构失效时对应的载荷循环次数在Case1与Case2之间。由此可知,各种工况按不同排列方式产生的载荷谱对疲劳寿命的影响显著。
组合多种工况生成疲劳载荷谱,各种工况的载荷谱块所占疲劳载荷谱的比例和组合方式对结构的疲劳寿命影响显著。在实际工程中,为保守起见,首先考虑将主导载荷工况的名义应力范围作为疲劳载荷进行疲劳寿命评估。
7 结 语
根据中国船级社最新修正的《船体结构疲劳强度指南》计算得到集装箱船纵骨节点的名义应力范围,将名义应力范围的长期分布服从两参数的Weibull分布的随机数作为疲劳载荷,结合BS7910的十字接头焊趾处表面裂纹应力强度因子经验公式及裂纹扩展单一曲线模型,给出大型集装箱船甲板扁钢型纵骨端部连接节点的疲劳寿命评估方法,并进行实例分析,得到以下结论:
1) 通过简化应力分析求取名义应力范围,使得疲劳载荷的计算相对简单且便于操作。
2) 扁钢型纵骨端部连接节点焊趾处表面裂纹的应力强度因子可采用 BS7910的十字接头焊趾处表面裂纹应力强度因子经验公式计算。
3) 选用主导载荷工况对应的名义应力范围生成的疲劳载荷谱,且考虑平均应力和残余应力的影响,因此结构所受的疲劳载荷较大,疲劳寿命分析结果偏于保守,可为高强度钢厚板纵骨设计和船舶营运中疲劳寿命评估提供参考。
4) 利用组合多种工况生成疲劳载荷谱,各工况在船舶疲劳寿命中所占的比例和组合方式对结构的疲劳寿命有较大影响,准确模拟实际船舶的疲劳载荷谱对预报疲劳寿命有着重要的意义。
[1] 韩钰,陈磊,王伟飞,等. 超大型集装箱船的结构设计[J]. 船舶与海洋工程,2015, 31(4): 10-17.
[2] 黄小平,韩芸,崔维成,等. 变幅载荷作用下焊接接头疲劳寿命预测方法[J]. 船舶力学,2005, 9(1): 89-97.
[3] 刘帆,黄小平. 集装箱船典型疲劳评估节点应力强度因子计算[J]. 中国造船,2015, 56(1): 27-40.
[4] 韩芸,黄小平,崔维成,等. T 型接头焊趾表面裂纹应力强度因子的简化计算方法[J]. 中国造船,2006, 47(1): 1-11.
[5] BOWNESS D, LEE M M K. Prediction of weld toe magnification factors for semi-elliptical cracks in T–butt joints [J]. International Journal of Fatigue, 2000, 22(5): 369-387.
[6] BS Institution. Guide to methods for assessing the acceptability of flaws in metallic structures: BS7910[S]. British Standards Institution, 2000.
[7] FU B, HASWELL J V, BETTESS P. Weld magnification factors for semi-elliptical surface cracks in fillet welded T-butt joint models [J]. International Journal of Fracture, 1993, 63(2): 155-171.
[8] 潘希颖. 82000dwt散货船底部纵骨节点疲劳分析优化[J]. 船舶与海洋工程,2015, 31(1): 20-24.
[9] 中国船级社. 船体结构疲劳强度指南[M]. 北京:人民交通出版社,2014.
[10] HUANG X, MOAN T. Improved modeling of the effect of R-ratio on crack growth rate [J]. International Journal of Fatigue, 2007, 29(4): 591-602.
[11] HUANG X. Fatigue crack growth rate recommended in BS7910 and a unique crack growth rate curve under different load ratios[C]//ASME 2007 Pressure Vessels and Piping Conference. American Society of Mechanical Engineers, 2007: 305-311.
[12] HUANG X, TORGEIR M, CUI W. An engineering model of fatigue crack growth under variable amplitude loading [J]. International Journal of Fatigue, 2008, 30(1): 2-10.
[13] 冯国庆. 船舶结构疲劳强度评估方法研究[D]. 哈尔滨:哈尔滨工程大学,2006.
A Fatigue Life Prediction Method for Longitudinal Deck Stiffener Nodes in Large Container Vessels
LUO Pan,HUANG Xiao-ping,KONG Xiao-bing
(Collaborative Innovation Center for Advanced Ship and Deep-sea Exploration, Shanghai Jiao Tong University, Shanghai 200240, China)
A crack propagation fatigue life prediction method based on fracture mechanics is used in this paper to estimate the fatigue life of longitudinal deck stiffeners made of high tensile steels on large container vessels. The prediction is based on the nominal stress of the longitudinal stiffeners calculated with the fatigue load formula expressed in Guidelines for Fatigue Strength Analyses of Ship Structures, the empirical formula for longitudinal stiffener weld toe surface crack stress intensity factor and the unique crack growth rate model. Numerical calculations on the connecting surface crack stress intensity factor of flat steel longitudinal stiffeners show that there is little difference between the factors obtained and the factors calculated according to the empirical formula in BS7910 for cruciform joint weld toe surface crack stress intensity, thus the formula is identified to be used to calculate the longitudinal stiffener end surface crack stress intensity factors. Fatigue life prediction for the weld toe of typical longitudinal deck stiffener node in some large containership is performed based on various load spectra composed of different loading conditions in order to discuss the influence of different fatigue spectra on fatigue crack propagation.
longitudinal deck stiffeners; crack propagation; stress intensity factor; fatigue life prediction
U674.131;U661.4
A
2095-4069 (2016) 06-0001-010
2016-07-07
国家自然科学基金(51279102)
罗盼,男,硕士生,1991年生。研究方向为船舶结构强度分析。
10.14056/j.cnki.naoe.2016.06.002

