压缩映射原理

刘海军

（甘肃省兰州市永登县第二中学,甘肃 兰州 730300）

压缩映射原理

刘海军

（甘肃省兰州市永登县第二中学,甘肃 兰州 730300）

本文介绍压缩映射原理的内容和几何描述及其压缩映射原理的代数证明和几何证明,并且论述了压缩映射原理在求数列极限、线性代数方程组、微分方程、积分方程、数学模型方面和许多关于存在唯一性定理证明中的应用,在一些特殊的、复杂的微分方程、代数方程、积分方程等方程中,它不仅可以用来证明存在唯一性定理,而且也提供了对方程求解的方法———逐次逼近法,并很广泛地被运用在求极限的问题上，同时论述了压缩映射原理的推广和证明及其在具体实例中的应用。

不动点;压缩映射原理;数列;微分;积分

1 引言

压缩映射原理是泛函分析中的一个最常用、最简单的存在性定理。本文通过论述压缩映射原理及其应用,并通过具体实例来说明用它可以处理一些利用分析方法比较难解决的问题。

2 压缩映射原理的证明

压缩映射理的背景：取一个浅盒和一张纸，纸恰好盖住盒内的底面，可想而知此时纸上的每个点与正在它下面的盒底上的那些点配成对。把这张纸拿起来，随机地揉成一个小球，再把小球扔进盒里。拓扑学家已经证明，不管小球是怎样揉成的，也不管它落在盒底的什么地方，在揉成小球的纸上至少有一个这样的点，它恰好处在它盒底原来配对点的正上方.这个点就是我们要找的不动点，如何找这个点呢？

注解:纸被揉成球以后，看它现在投到纸盒底部的影子.纸盒底部的影子区域肯定比纸盒底要小。那么，就取【纸盒底部的在影子内的那个部分】，它肯定对应于纸团里面的某一小团部分.（因为整个底板对应于整个纸团，那么底板的一部分就肯定对应于一部分纸团）,假如去掉纸团的其他部分，那一小团部分同样可以在纸盒底面投影，而且投影肯定比刚才的大投影小，而且在它之内。（因为它是在整个纸团之内）。那么，取这一小片投影（注意这片影子肯定是连续的不会断开，因为纸没有撕裂），当它再往纸团里对应的时候，肯定对应于其中更小的一团。我们再次把多余的纸去掉.就是说：整个纸盒底对应于纸团,纸盒【在纸团投影内的部分】对应于纸团内的一小块,纸盒【一小块的投影的部分】对应于刚才那一小块内的更小一块,纸盒【更小块投影的部分】对应于更小块中的更更小一块，如此下去，不断地去掉纸无限次，最后纸团只剩下了一个点，它的投影就对应于纸盒的一个点。

3 压缩映射原理的推广及其应用

3.1 压缩映射原理的推广

定理3.2（Browder不动点定理）:设En为有限维赋范空间，为有界凸闭集，:连续，则A在中至少有一个动点。

3.2 压缩映射原理的应用

3.2.1 不动点定理在求数列极限中的应用

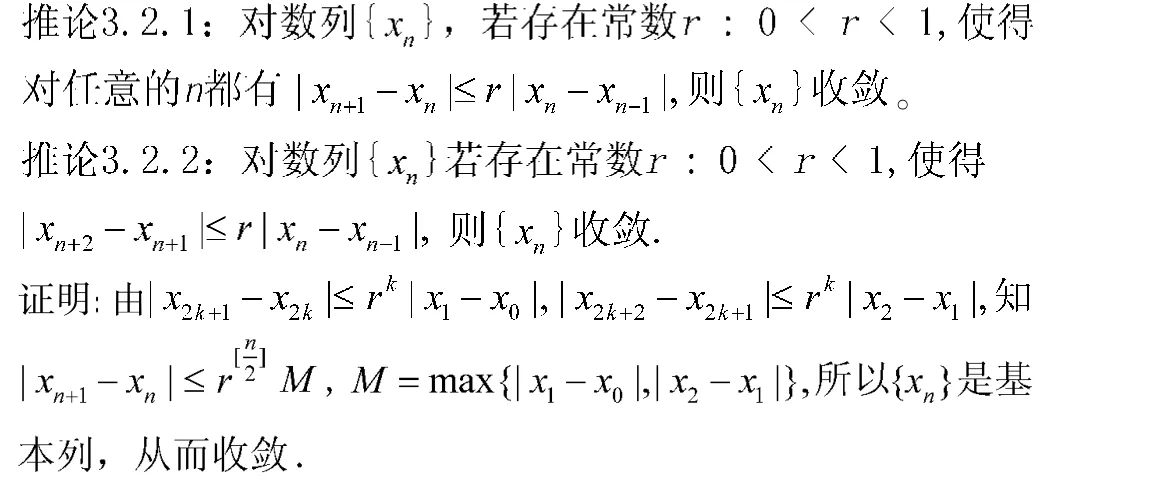
下面我们看一下不动点原理在求数列极限中的应用

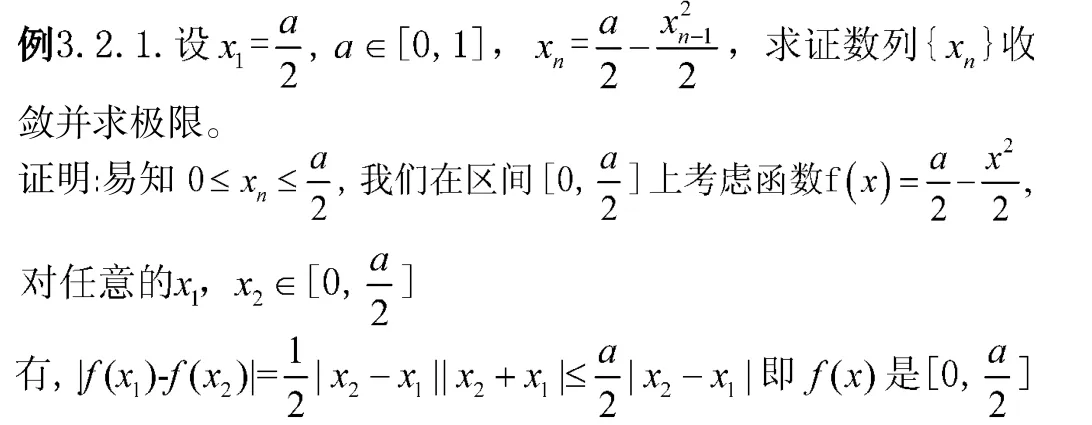
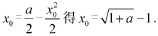
3.2.2 不动点定理在积分方面的应用

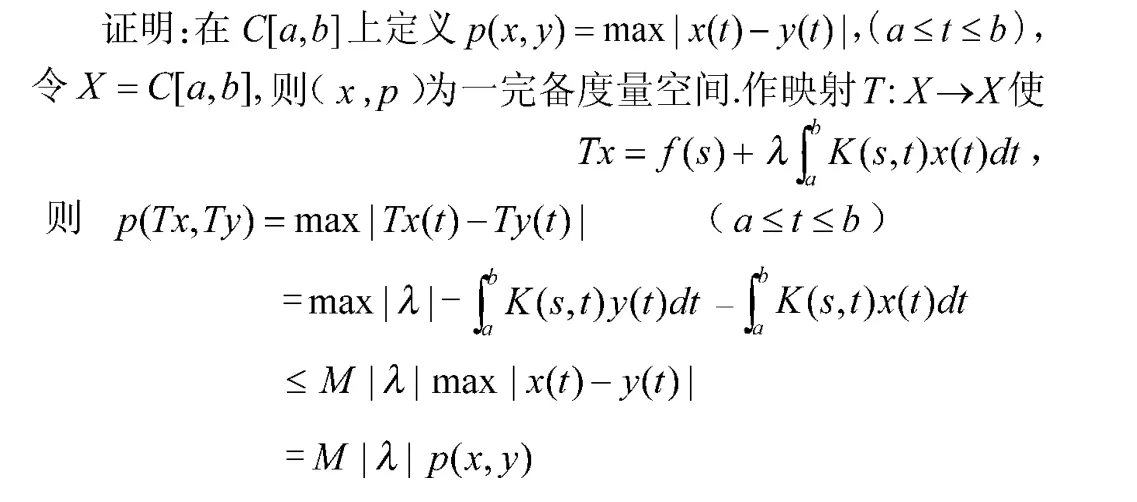
3.2.3 不动点原理在数学模型中的应用

如果函数f（x）在［a，b］是一个连续函数，则根据连续函数的介值性定理可知：

推论4.若函数f（x）在f（［a，b］）h（θ）x连续且满足f（［a，b］）则f（x）在［a，b］至少有一个不动点。

例3.2.5.1 日常生活中会有这样的体验：把椅子放在不平的地面上时通常三条腿着地放不稳,但是稍微挪动几次就可以使四条腿着地而放平稳。现我们把该现象建模为一个数学问题，通过不动点定理来进行解释。

解：模型假设：（1）椅子四条腿长度一样，与地面接触为一点，且四点连线为正方形。

（2）地面高度连续变化。

（3）椅子在任何位置都有三只腿着地。（4）椅子转动时中心不变。

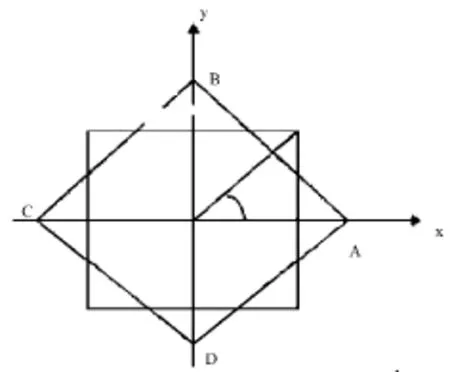
图1

模型建立及求解：设着地点为A,B,C,D建立如图坐标系，设θ为AC转动后和x轴夹角，显然f（θ）为A，C两点于地面距离之和,g（θ）为B，D两点于地面距离之和。

由地面平坦假设知f（θ）,g（θ）均连续,由椅子至少三条腿着地知对任意θ，f（θ），g（θ）至少有一个为零。

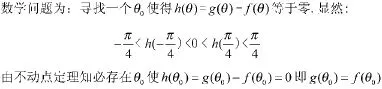
4 对压缩映射原理的看法

数学分析中最重要的一部分知识是微积分,它是处理一系列数学问题,甚至其它学科的基础工具,在解答微积分问题时,经常遇到很多有关存在唯一性问题。压缩映射在几何上的意思是说点x和y经T映射后,它们像的距离d（Tx,Ty）缩短了,不超过原像距离d（x,y）的a倍（a<1）。通过逐次逼近的方法，总可以找到方程的唯一解和数列的极限。

因此压缩映射原理在数学分析、微分方程、积分方程、代数方程解的存在唯一性定理证明中起了重要作用。

[1]张恭庆.泛函分析讲义[M].北京大学出版社，1999.

[2]裴礼文.数学分析中的典型问题与方法[M].高等教育出版社，2002.

[3]龚怀云.应用泛函分析[M].西安交通大学出版社，2001.

[4]李大华.应用泛函教程[M].华中理工大学出版社，1999.

[5]安国胜.揭开不动点法求数列通项公式的神秘面纱[J].甘肃教育，2007，（47）.

[6]谷学伟等.不动点理论及其应用[M].太原师范学院学报(自然科学版)，2009.

[7]韩超.数学分析中的不动点问题[J].哈尔滨师范大学自然科学学报，2006.

[8]李庆扬等.数值分析[M].清华大学出版社，2009.

[9]邢家省.压缩迭代序列的极限及其应用[J]河南科学，2008.

[10]程其襄等.实变函数与泛函分析基础[M].高等教育出版社，1983.