基于遗传算法的小波神经网络在地震形变前兆分析中的应用

袁国旭，任峻峰，李文军，王向亮

(1.河北省地震局承德地震台，河北承德 067000； 2.河北省地震局宽城地震台，河北宽城 067600)

基于遗传算法的小波神经网络在地震形变前兆分析中的应用

袁国旭1，任峻峰1，李文军1，王向亮2

(1.河北省地震局承德地震台，河北承德 067000； 2.河北省地震局宽城地震台，河北宽城 067600)

利用遗传算法来优化小波神经网络,达到提高逼近精度,简化网络结构，并利用优化后的小波神经网络训练地震前兆形变资料,运用MATLAB 对拟合和预测过程进行仿真。结果表明，该方法对地震预测有参考作用。

遗传算法；小波；神经网络；地震预测

0 引 言

地震是极其复杂的物理过程,其孕育、发展、发生相当缓慢。伴随这一现象的发生，地壳会发生一系列的形变变化。地震形变前兆观测是捕捉这一变化的有利观测手段。从2002年起，中国的形变观测发展到数字化观测阶段，记录保存了大量丰富的数字化观测资料。大量的地震前兆形变数据蕴涵着可用于预测未来地震的某种信息,这也是人们对其进行预测的基础[1]。

小波神经网络是将小波变换和神经网络理论结合起来的一种神经网络。它是基于小波分析理论所构造的一种分层的、多分辨率的新型人工神经网络。小波神经网络具有更多的自由度，具有更灵活有效的函数逼近能力和较强的容错能力。

遗传算法是一种借鉴生物界自然选择和自然遗传机制的随机搜索算法。它的优越性主要表现在：(1)具有群体搜索和内在启发式随机搜索的特性，不易陷入局部最优；(2)遗传算法固有的并行性和并行计算的能力，非常适用于大规模并行计算。

1 小波神经网络结构及其算法

1.1 小波理论

小波变换最早是1984年研究地震资料而使用的。由于小波分析具有能够根据分析对象自动调整参数的“自适应性”和能够根据观测对象自动“调焦”的特性，可以较好地用于地震资料分析。

小波变换是一种信号—时间(频率—幅度)分析方法，它具有多分辨多分析的特点，在时频两域都具有表征信号局部特征的能力。小波变换是指某一基本小波函数ψ(t)平移b后，再在不同尺度a下与待分析的时间序列信号x(t)做内积。

(1)

等效的时域表达式为：

(2)

设θ(t)为具有低通性质的平滑函数，以它的一阶、二阶导数作为小波对f(t)做小波变换，可以证明：

Wφ1f(α,τ)=f(t)⊗φ1(αt)

(3)

(4)

式中，⊗表示卷积，也就是说φ1(t)、φ2(t)对f(t)作小波变换，分别相当于f(t)被θ(t)平滑后再对t求一阶或二阶导数。因此，对某一固定a值，f(t)⊗θ(t)的拐点既是Wφ1f(α,τ)的极值点，又是Wφ2f(α,τ)的过零点，由此可检测信号的急剧变化之处。

本研究中所采用的低通性质的平滑函数为高斯函数，根据它的一阶、二阶导数(墨西哥草帽小波函数)作为小波基函数进行突变点分析。之所以选择此函数是因为它具有对称、可微、可积，和时频两域都是高斯型且呈平方型指数衰减特性，在时频两域均具有很好的局域性。由此看出，小波分析能够通过小波基函数的变换分析信号的局部特征，并且在二维情况下具有信号方向选择性能力。

1.2 小波神经网络模型结构及算法

小波神经网络的理论基础是小波函数的重构理论：对于满足容许性条件的母小波,其伸缩和平移形成的连续小波基的线性组合在L2(R)中稠密。本文的小波神经网络结构采用3层结构,已有理论证明只含有一个隐含层的3层前馈网络能以任意精度逼近一个非线性映射。小波神经网络结构设计，即如何选取隐层层数及其节点数，目前基本上依赖于经验公式[2]。具体设计时，还需结合经验公式进行试凑。对一般问题，选用一个隐层即可，这是由Komogorov 定理[3]决定的。小波神经网络结构如图1所示。

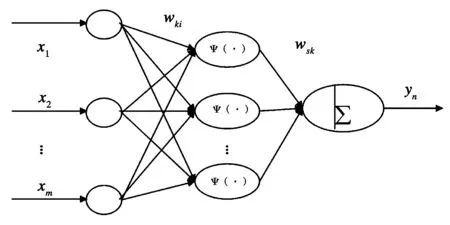
图1 小波神经网络结构图

设函数ψ(t)满足容许条件:

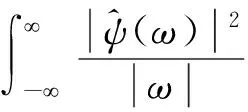
(5)

则称ψ(t)为基小波，式(3)称为容许条件，那么可数集合:

(6)

满足框架性质， 即存在2个常数:

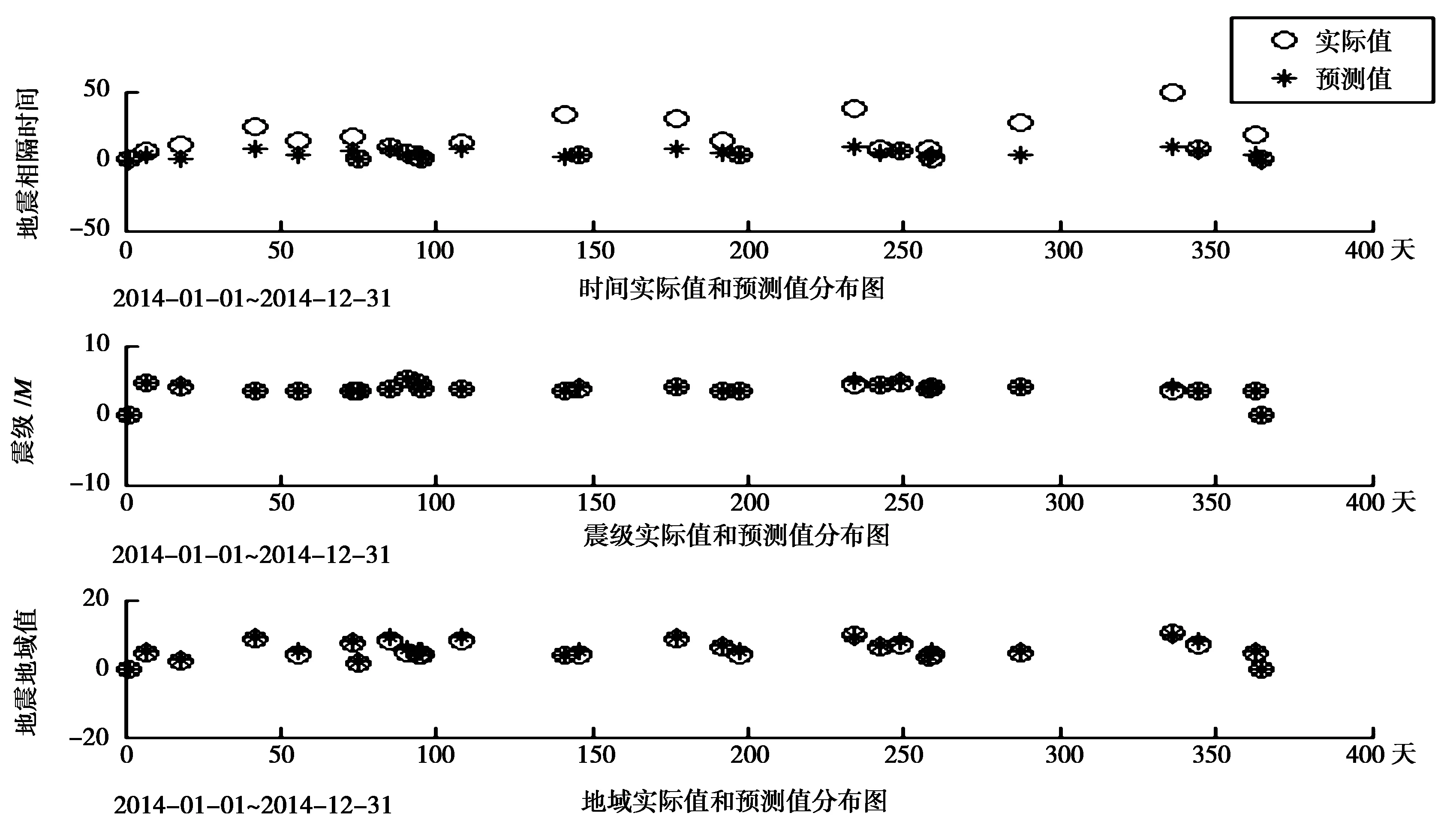
0

(7)

式(5)表明,框架φ在L2(R)中是稠密的，既使框架φ中元素的所有线性组合的集合：

(8)

在L2(R)中是稠密的。式中，j为小波基的个数。对于具有m个输入，n个输出的网络，式(6)变为：

(9)

在式(7) 中，采用使用较多的Morlet母小波(墨西哥草帽小波函数)，即：

ψ(x)=cos(1.75x)exp(-0.5x2)

(10)

对于输入输出为(xt,?yt)(t=1,2…,n)的N个样本对，确定网络参数Wki，ak,bk和Wsk，可以通过下述误差能量函数进行调整:

Et=0.5(y(xt)-yt)2

(11)

2 遗传算法优化网络初始值训练

小波神经网络是根据误差能量函数采用梯度下降法调整网络连接权值和伸缩平移尺度。但此法易陷入局部极小和引起振荡效应。为此，本文应用遗传算法较强的全局搜索能力优化网络初始值。其原理如图2。

其步骤如下：

步骤1:群体初始化：随机产生L个结构，对每个结构编码，其结构编码长度为：

m×j+j+j+j×n。

步骤2:将神经网络的各个权值及伸缩平移尺度按次序编成一个字符串作为问题的一个解。其形式如下：

图2 遗传算法优化小波神经网络的过程

其中，k=1,2,…,n,…,j，然后对编码后的初始群体进行训练。

步骤3:根据训练结果确定每个个体的适应度值。

Fitness=1/(1+E)

(12)

步骤4:若终止条件满足，则转步骤7。

步骤5:选择若干适应度最大的个体，直接继承给下一代。同时用父代适应度最大个体替代遗传操作后产生的最差个体。

步骤6:对当前一代群体进行交叉和变异等遗传操作，产生下一代群体，转步骤3。

步骤7:终止循环，得到最佳染色体。然后：解码还原相应值。

3 资料选取与预处理

设地震发生的时间序列为{X(t)},对其进行预测可用下式描述：

(13)

即用神经网络来拟合函数f，然后预测未来值。如何根据不同对象的时间序列找到式(11)中输入量维数m是建立预测模型的关键一步,这是相空间重构问题。 为了能够从时间序列中得到动力系统相空间的几何结构，Packard[ 4 ]等人采用时间延滞技术,把一维时间序列嵌入到m维空间中。

X(t)={x(t),x(t-τ),x(t-2τ),…x(t-(m-1)τ)}

(14)

式(14)表示t时刻系统动力学状态,τ为滞时,m为嵌入维数。得到τ和m就可以确定预测模型输入向量和小波神经网络输入层数。可见预测问题和函数逼近问题是等价的[ 5-10 ]。选取大华北地区(32°～43°N，108°～130°E)2002～2014年震级不小于3.5级的震例。每个震例的三要素经过相应的处理：时间采用的是地震间隔时间。震级基本不变，同一天发生的地震采用震级较大的地震，余震一般不予考虑。地点采用9区间表示法，即把大华北地区划分为9个小区间。

选用的地震形变前兆资料为2002年到2014年河北省怀来地震台水管、宽城地震台体应变和垂直摆、易县地震台伸缩仪、涉县地震台垂直摆各测项日均值数据，共计11个分项，基本涵盖了地震前兆形变各数字化观测手段的资料。其中2002～2013年数据为训练数据，2014年为测试数据。资料选用的标准为内在精度较高、在中国地震局资料评比中和河北地震省局资料评比中多次获奖的形变前兆手段。地震形变前兆数据经过插值处理。

4 仿真结果

仿真的实验步骤为：

(1)把经过插值处理的数据进行归一化处理；

(2)利用遗传算法对处理后的2002年到2013年数据优化网络初值训练；

(3)对所有数据进行小波变换处理；

(4)把去噪后的数据进行归一化处理；

(5)用2014年数据进行网络测试，验证网络的预测能力；

(6)网络运行后对数据进行还原。

实验结果表明：

(1)基于遗传算法优化的小波神经网络对地震三要素有一定的预测能力。从图3地震三要素中实际值和预测值分布图中来看，震级和地域的预测较好，时间的预测较差。其中的原因可能是地震发生间隔时间从1天到49天不等，波动较大，预测有一定的难度。

(2)用2014年数据进行网络测试，验证了网络的预测能力。从图4遗传算法优化种群均值变化和解的变化来看，经过50代的遗传迭代的优化已达到较高的精度。由于2014年不小于3.5级的震例仅有25例，相对较少，最为重要的时间要素预测误差较大，从图5地震三要素的均方根误差分布图来看，时间的预测误差较大，需要改进相关算法。

(3)从实验的结果来看，改进相关算法最直接的方法是增加数据样本，即增加用于训练数据和测试数据的震例，可选取震级大于2.5级或3级的震例，震级太小的震例研究价值不大。另一种可能的方法是选取的地震形变前兆资料由日均值变为时值甚至到分钟值，但过多的数据量可能会影响效率。另外，由于数字化的河北地震形变前兆资料里大震强震震例太少，暂时无法验证。

图3 地震三要素中实际值和预测值分布

图4 遗传算法优化种群均值变化和解的变化

图5 地震三要素的均方根误差分布

5 结 语

基于遗传算法的小波神经网络基本上达到较高的预测精度，也达到较快的收敛速度，充分发挥了遗传算法的全局优化搜索能力和小波变换良好时频局部特性。从实验结果看, 对地震三要素的预测问题, 基于遗传算法的小波神经网络是一种值得继续深入探讨的方法。

[1] 韩晓飞,潘存英，罗词建. 基于遗传算法的广义回归神经网络在地震预测中的应用[J].华北地震科学,2012，30(1):48-53.

[2] 叶斌,雷燕. 关于BP 网中隐含层层数及其节点数选取方法浅析[J]. 商丘职业技术学院学报,2004，3(15):52-60.

[3] 郭海涛,张殿伦,马国芳. 使用BP 算法应考虑的若干问题[J] . 佳木斯大学学报(自然科学版),2000，18(4):363-365.

[4] PACKARD N,CRUTCHIELD J, FARMER D,et al.Geometry From A Time Series[J].Physial Review Letters,1980，45:712-715.

[5] 吕淑萍,赵咏梅. 基于小波神经网络的时间序列预报方法及应用[J].哈尔滨工程大学学报，2004,25(2):180-182.

[6] 李逊,谢红胜. 基于遗传算法的小波神经网络[J] . 计算机与数字工程 ,2007,35(8):5-7.

[7] 魏立龙,许东方，孙浩，等. 基于遗传算法的小波神经网络在股票预测中的应用[J]. 信息与电脑,2011(5):130-131.

[8] 李婧瑜,李歧强，侯海燕，等. 基于遗传算法的小波神经网络的交通流预测[J]. 山东大学学报(工学版),2007，37(2):109-112.

[9] 徐强,束龙仓，杨桂莲，等.基于遗传算法优化的小波神经网络在地下水位预测中的应用[J]. 水文,2010，30(2):27-30.

[10]万永革.数字信号处理的MATLAB实现(第二版)[M].北京：科学出版社,2012：27-39.

WAVELET NEURAL NETWORK BASED ON GENETIC ALGORITHM IN THE APPLICATION OF SEISMIC DEFORMATION PRECURSOR ANALYSIS

YUAN Guoxu1，REN Junfeng1，LI Wengjun1，WANG Xiangliang2

(1.ChengdeSeismicStation,EarthquakeAdministrationOfHebeiProvince,Chengde067000,China;2.KuanchengSeismicStation,EarthquakeAdministrationOfHebeiProvince,Kuancheng067600,China)

The wavelet neural network is optimized by genetic algorithm in order to improve the approximation accuracy and simplify network structure, and the results are used to train the earthquake precursor deformation data.The fitting and forecasting process are simulated by the MATLAB.The results show that the method has reference function for earthquake prediction.

Genetic algorithm; Wavelet; Neural network; Earthquake prediction

2016-01-21

袁国旭(1970— )，男(满族)，河北宽城人，工程师，本科学历，从事地震监测与管理工作。

P315-39

A

1005-586X(2016)04-0049-06