基于互联互通的城轨网络化运营行车交路策略研究

任 飞，王 伟，李 腾，张 可

（1.北京交通大学 电子信息工程学院，北京 100044；2.城市轨道交通北京实验室，北京 100044 ；3.辽宁科技大学 电子与信息工程学院，鞍山 114051）

基于互联互通的城轨网络化运营行车交路策略研究

任 飞1，王 伟2，李 腾1，张 可3

（1.北京交通大学 电子信息工程学院，北京 100044；2.城市轨道交通北京实验室，北京 100044 ；3.辽宁科技大学 电子与信息工程学院，鞍山 114051）

本文针对城市轨道交通互联互通的网络化运输场景，对其行车交路方案进行研究。通过对互联互通下交路新特征的分析，提出了交路方案设计方法，建立了交路方案的多目标优化模型及相应的求解方法，并通过实例分析验证了该方法的可行性。

网络化运营；互联互通；行车交路；多目标优化模型

随着城市轨道交通的迅猛发展，原来单一独立的线路形态逐渐向大规模、网络化方向迈进。然而，已经建成的城市轨道交通网络是建立在旅客不断换乘的基础上实现的，并不是真正意义上的“网络化”。真正的轨道交通网络化应实现不同线路和车辆之间的互联互通。

城市轨道交通互联互通的定义是：列车可以在一条以上的线路上安全运营，并且要求相对应的车辆、信号、通信、供电、线路限界和运营商等方面能够一致，即实现列车在不同线路之间的跨线、共线、越线运行。实现城市轨道交通互联互通网络化运营具有重要的现实意义。从乘客服务角度，乘客出行无需经过复杂的换乘过程，减小了换乘时间，提高了服务质量。从运营方角度，可以实现资源共享，提高资源利用效率和运营组织的灵活性。

行车交路方案作为运输组织的重要内容，规定了各列车运行的区段以及对应的开行对数。目前，对交路方案的研究大多针对单线独立运营场景，本文借鉴我国高速铁路相关研究成果，对互联互通下交路进行分析，提出了交路方案的设计方法，并选取两条互联互通的城市轨道交通线路作为研究对象，以候车时间最小化、换乘客流最小化、企业运营成本最小化为目标建立了交路方案多目标优化模型以及求解方法，最后通过实例进行了应用验证。

1 交路方案设计

交路方案主要是根据客流分布以及相关线路条件限制进行设计。交路的起讫车站和开行对数是交路方案设计的两个要素。与单线运输形式相比，互联互通线路网络运输具有以下新特征：

（1）交路形式更加复杂多样。非互联互通下运行交路形式单一简单化，按运行区间的长短基本包括大交路和小交路两种形式。而互联互通下由于列车可以实现跨线运行，因此行车交路形式更为多样化，运输组织方式也更加灵活。

（2）列车运行范围更加通达。列车不必只在本条线路范围内运行，可以跨越到其它相邻线路，延伸了列车服务范围。

（3）客流直达率提高，换乘客流减少。单线运输条件下，跨线客流只能通过换乘的方式到达目的地。而互联互通下，若存在相应的跨线运行交路，跨线客流可以选择对应直达列车实现不换乘。

1.1 客流分解

“按流开车”是交路设计的根本原则，每种交路的设置总是为特定客流服务的。因此，对OD客流进行深入分析是制定交路方案的前提。互联互通下，输送客流可以分为两类：本线客流和跨线客流。本线客流的运输任务主要靠本线交路来完成，跨线客流靠跨线交路实现。因此，将OD客流进行分解，根据本线客流和跨线客流分布特点分别进行设计。

1.2 本线交路设计

本线交路根据OD客流分解后的本线OD客流分布进行设计。具体包括以下步骤：

（1) 尽量遵守原来单线运输时列车开行规律。由于各条线路设计初期，必然是经过研究后确定的客流交换量较大的路径。因此，本线客流一定是主要的服务对象，为了不打破这部分客流长期以来已经形成的相对稳定的出行规律，尽量遵循原来单线运输的交路方案。

（2）根据单向断面客流量分布确定。借鉴传统单线运输交路方案设计原则，根据单向断面客流量分布情况进行本线交路设计。考虑到实际运营情况，一般均设置本线大交路，对于明显断面客流量较大的部分区间可以考虑开行本线小交路。各交路开行列车数根据具体客流量大小进行合理分配。

1.3 跨线交路设计

跨线交路根据OD客流分解后的跨线OD客流分布进行设计。具体包括以下步骤：

（1）归并OD客流。由于某些车站不具备折返能力，因此，首先将各普通车站OD客流归并到相邻的折返车站OD间，归并得出折返站间OD客流。

（2）跨线客流强度满足跨线列车开行的最低OD客流量。设置开行跨线交路的最低客流量限制，当归并后的折返站间OD流量大于设置最低流量时，可将此选为备选跨线交路。

（3）综合考虑跨线列车交路个数和列车数。各交路开行列车数根据客流情况合理分配。考虑到实际运营复杂性和对本线列车的运营能力的影响，跨线交路个数以及跨线列车开行比例宜控制在合理的范围内。

通过以上设计思路可以初步得出备选交路方案，下面介绍交路方案的优化方法。

2 交路方案的优化模型

选取某非高峰小时的OD客流分布数据及备选交路方案作为交路方案优化的输入条件。选取乘客候车时间、直达性、企业运营成本作为优化指标。研究的优化问题可归纳为：已知线网OD客流分布及相关线路参数，确定列车运行各交路的起讫点及对应列车开行对数，在满足各种约束条件的前提下，使得乘客候车时间最小化、换乘客流最小化、企业运营成本最小化。

2.1 模型假设

（1）所有列车采用统一的编组方案和站站停的停站方案。

（2）若有直达列车乘客首选直达列车到达目的地。OD区间内所有可直达列车平均分担该OD客流。

（3）所有列车在各区间运行速度相同，按平均旅行速度计算。

2.2 参数说明

基于以上假设，设轨道交通网络中有两条互联互通线路：线路1和线路2。线路1有n个车站，线路2有m个车站，两条线路均包含Q站，且Q站为跨线车站。线路1（线路2）的列车可以在Q站通过联络线跨线运行至线路2（线路1）。为了便于模型的抽象描述，下面定义一些符号：

路网：G=(S,E)描述。其中，S为所有车站集合，E为所有区间的集合。

车站：S={si|1≤i≤n+m-1}，其中：线路1车站集合S1={si|1≤i≤n}（Q站为sq1）；线路2车站集合S2={si|n+1≤i≤n+m}（Q站为sq2），sq1=sq2。另外，Sr={S1,…,Sn'}⊆S表示所有具备双向折返能力车站的集合。

区间：E={ei|1≤i≤n+m-2}，按车站标号顺序进行标记。

客流分布：Pod表示由SO站到Sd站的客流量；Pi表示区间ei最大单向断面客流量。

决策变量：xab为0～1变量，表示以Sa和Sb为两端折返站的交路是否选入交路方案中，是为1，不是为0；nab为整数变量，表示以Sa和Sb为两端折返站的交路每小时开行列车对数。

2.3 目标函数

2.3.1 目标函数1：换乘客流最小化

城市轨道交通实现互联互通的目的是满足乘客对直达的运营要求，尽量减少乘客换乘。因此，把实现换乘客流（Z1）最小化作为一个优化目标。

由以上假设，只要O 车站到D 车站至少被同一交路覆盖，则从O 站到D 站的乘客就可以直达，不需要换乘。因此，Z1的来源于OD车站之间没有共同交路覆盖的OD客流。设φ(x)为阶跃函数（x＜1值为0，x≥1值为1），则目标函数1可以表示为：

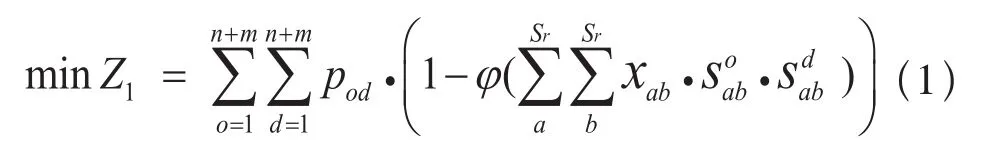
2.3.2 目标函数2：候车时间最小化

开行多种交路的列车，虽然减小了换乘给乘客带来的不便，但由于可乘坐的列车相对减小，导致部分乘客候车时间的增加。而乘客的候车时间体现了乘客出行的时间成本，因此尽可能缩小乘客候车时间是另一个关键的优化目标。

根据概率论相关知识，乘客候车时间的期望值为列车开行间隔时间的一半。则可直达乘客候车时间可表示为：

以上计算方法针对直达乘客，即只需进行一次候车；而换乘乘客则需在Q 站进行换乘，即需要进行两次候车。设可直达乘客（0，d）对集合A，不可直达乘客（0，d）对集合B。综上分析，可以得出全部乘客的候车时间，即目标函数2 表示为：

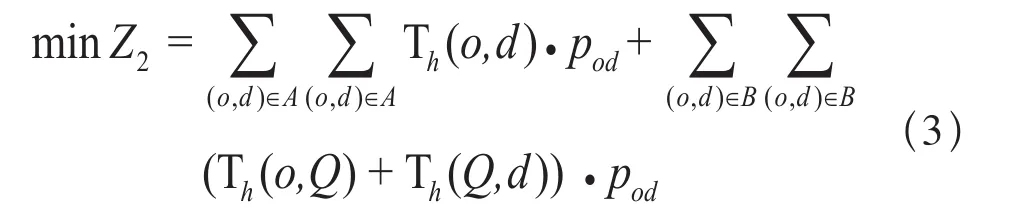
2.3.3 目标函数3：运营成本最小化

从运营方角度，应把运营成本最小化作为另一个优化目标。运营成本（Z3）主要由固定（Z固定）成本和变动成本（Z变动）组成。其中，Z固定主要包括车辆购置折旧成本，取决于车辆配备数量的大小；Z变动主要包括车辆走行消耗的费用（电力等资源耗费），主要取决于发车间隔以及交路长度。

通过相关公式计算，目标函数3 可以表示为：

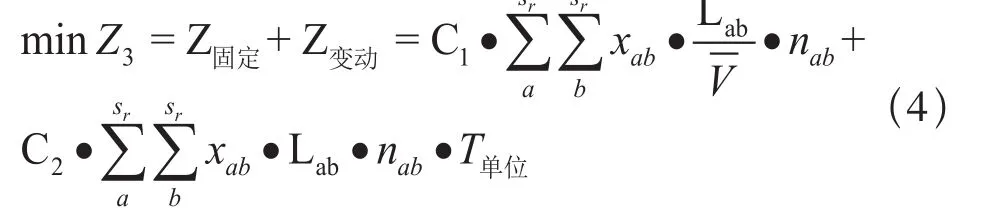
2.4 约束条件

（1）线网范围内交路总数应限制在合理范围。交路总数太少达不到运输服务要求，太多则导致运营组织复杂，并且不利于乘客引导。即：

（2）所有交路必须覆盖整个运营网络，确保任意区间至少有一条交路覆盖。另外，同一区间同时覆盖交路数应有上限。

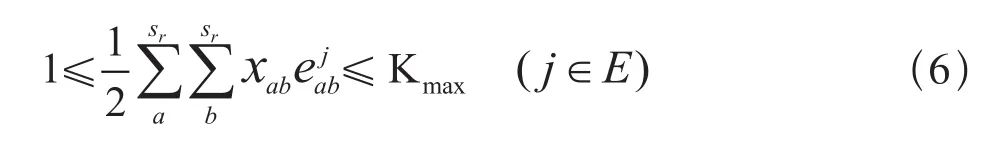
（3）列车在区间运行间隔限制在合适范围。既要保证基本的服务质量，又要满足区间通过能力要求。

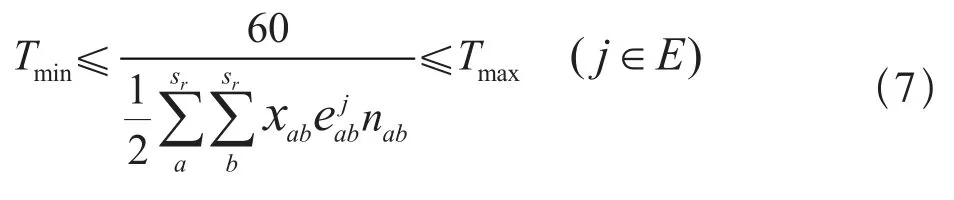
（4）满足各区段客流量需求。

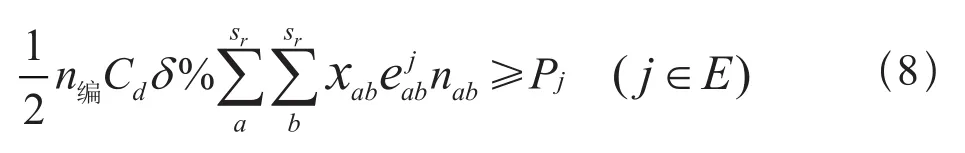
3 模型求解

上述模型中，有一组0～1决策变量xab和一组整数变量nab；优化目标函数有3个，具有非线性项；约束条件有4个，同时约束xab和nab。因此，该模型为多目标非线性0～1混合整数优化模型。该模型直接求解难度较大，然而3个目标函数均是求最小值解，可以将每个目标函数乘以一个权重因子，从而将多目标转化为单目标优化问题。为了统一衡量单位，用C换乘、 C时间分别表示每位乘客换乘的价值（元）、候车时间的价值（元）。并根据运营方的决策重点，对3个目标适当分配权重系数ρ1、ρ2、ρ3，则统一后的目标函数为：

其中：ρ1+ρ2+ρ3=1。

对于约束条件1，考虑交路的基本覆盖以及实际运营复杂性，取交路总数范围为：3～4个；对于约束条件3、4，考虑线路通过能力以及满足乘客基本服务水平，取列车区间运行间隔范围为：120～300 s。简化处理后该模型转化为单目标整数规划模型，可以借助计算机软件，如Matlab、Lingo等进行求解。

4 案例分析

某轨道交通线路网络由两条互联互通线路组成，线路A有6个车站，线路B有6个车站，其中，1、2、6、7、8、12站为双向折返车站，各站的站间距离如图1所示。表1为该轨道交通网络非高峰小时的OD客流，表2为模型中各参数的取值。

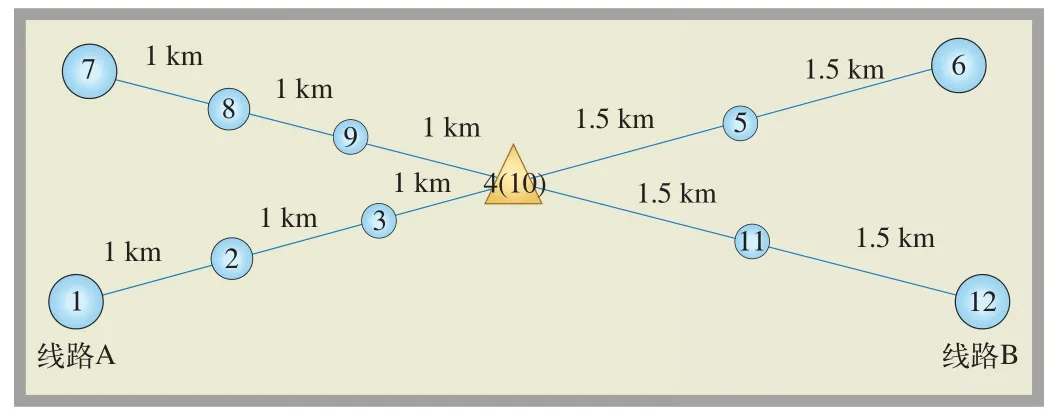
图1 互联互通轨道交通线网示意图

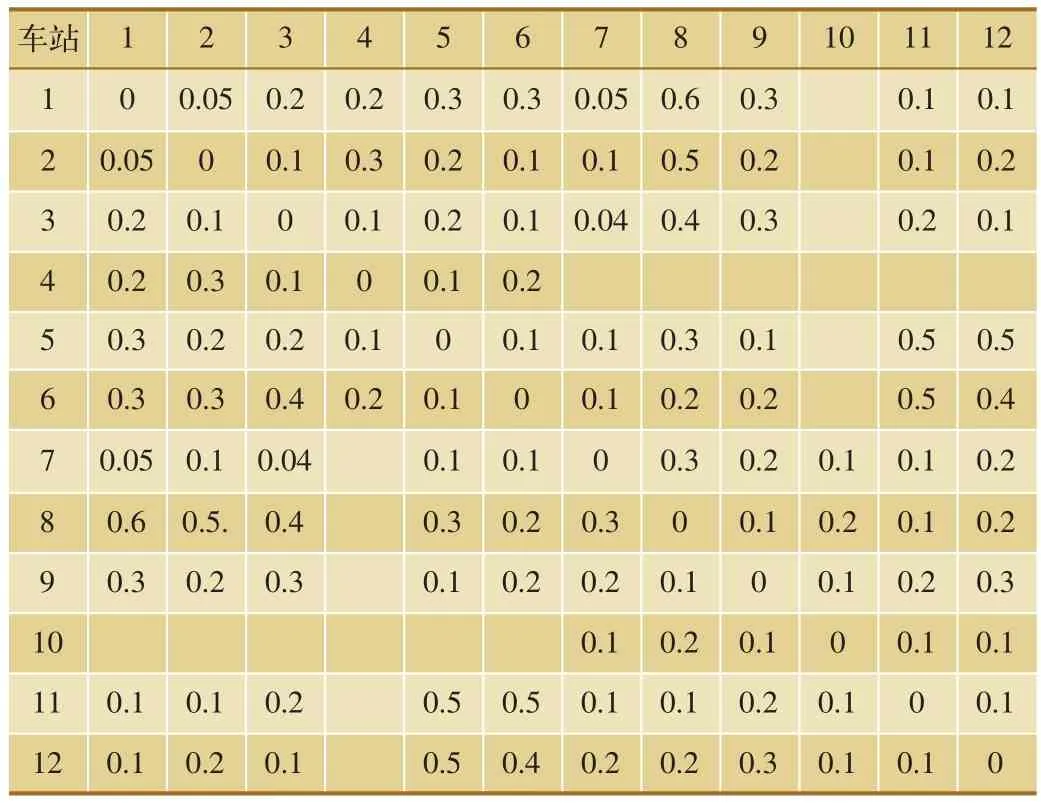
表1 非高峰小时OD客流/万人

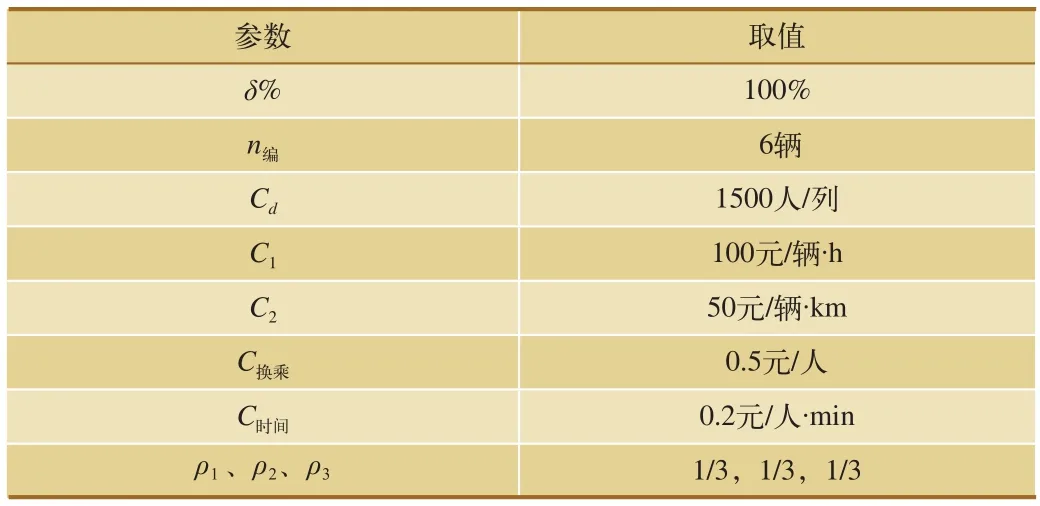
表2 相关参数取值

（1）对线路A和线路B的本线客流计算分析发现，其区间断面客流分布较为均匀，A线最大单向断面客流量为1.8万人/h，B线最大单向断面客流量为1.5万人/h。因此，本线交路可以确定为在A，B线路分别设置本线大交路作为备选方案。

（2）跨线交路OD对有以下几种：（1,7），（1,12），（6,7），（6,12），（2,8），（2,7），（2,12），（1,8），（6,8）。对跨线客流进行归并分析发现，（1,7），（1,8），（2,7），（2,8），（6,12）OD对间客流强度较大，可将其作为备选跨线交路方案。

（3）将相关参数代入优化模型中，通过Lingo优化求解软件对备选方案求解得想。x1,6=x7,12=x1,8=x6,12= 1，具体的最优开行方案如表3所示。

Strategy of traffc routing of network operation for Urban Transit based on interconnection

REN Fei1,WANG Wei2,LI Teng1,ZHANG Ke3
( 1.School of Electronic and Information Engineering,Beijing Jiaotong University,Beijing 100044,China;2.Beijing Laboratory of Urban Rail Transit,Beijing 100044,China;3.School of Electronic and Information Engineering,University of Science and Technology Liaoning,Anshan 114051,China)

According to the scene of interconnection network transport,this paper studied on the scheme of traffc routing.By analyzing the new features of the traffc routing based on interconnection,the design method of routing scheme was put forward.The multi-objective optimization model for routing scheme was established.The solving method of the model was also given.Finally,the feasibility of this method was verifed by case analysis.

network operation;interconnection;traffc routing;multi-objective optimization model

U231.92∶TP39

A

1005-8451（2016）05-0010-05

2015-11-03

北京高等学校青年英才计划（W1H100110）；北京市教委科研项目（W15H100030）；中央高校基本科研业务费项目（2015YJS008）。

任 飞，在读硕士研究生；王 伟，工程师 。