BDS与GPS三频模糊度解性能分析

刘礼衡，满小三，叶险峰

（1.湖南省第一测绘院，湖南 衡阳 421001；2.解放军信息工程大学，郑州 450001；3.湘潭大学能源工程学院，湖南 湘潭 411100）

BDS与GPS三频模糊度解性能分析

刘礼衡1，满小三2，叶险峰3

（1.湖南省第一测绘院，湖南 衡阳 421001；2.解放军信息工程大学，郑州 450001；3.湘潭大学能源工程学院，湖南 湘潭 411100）

随着BDS与GPS都已经播发三个频率，采用无几何无电离层模糊度解算方法，着重分析了BDS与GPS三频模糊度解算性能。通过二组BDS/GPS实测三频基线数据分析表明：BDS的载波相位多路径延迟比GPS更为严重，致使短基线BDS窄巷模糊度通过多个历元平滑无法收敛为正确值，而GPS可以通过多个历元可以平滑的收敛为正确值。

无几何无电离层；BDS；窄巷模糊度

【DOI】10.13616/j.cnki.gcjsysj.2016.07.145

1 引言

高精度GNSS定位的前提条件是正确的固定模糊度值。随着GPS现代化及我国北斗卫星导航系统逐步由区域卫星导航系统发展为全球卫星导航系统，且都播发3个频率的导航信号，频率的多样性可以提高无几何模糊度解算方法的可靠性[1]。

在三频情形下，一般采用TCAR算法解算模糊度，但是该算法的第二步和第三步很容易受到双差电离层残差的影响，尤其是第三步要求双差电离层残差在cm级，才能保证窄巷模糊度固定成功。即使在短基线的情况下，双差电离层残差也很容易到达cm级。由此可见，双差电离层残差是影响TCAR算法中宽巷及窄巷模糊度解算的关键因素。为提高模糊度固定成功率，必须要消除或减弱双差电离层残差的影响。一般对窄巷模糊度采用无几何无电离层模型[2]，通过多历元平滑获取正确的窄巷模糊度值。许多学者对三频模糊度解算的研究都是采用仿真数据，没有考虑实际情况的复杂性，比如载波相位多路径延迟。

文章通过实测数据分析了采用无几何无电离层模糊度解算的BDS与GPS模糊度的收敛时间及模糊度的收敛值，初步评估了BDS与GPS三频模糊度的解算性能。

2 无几何无电离层模糊度解算

几何无关（Geometry-free）模型是指采用多频伪距和相位组合观测值消除几何误差的模糊度求解模型，考虑几何无关模型中电离层延迟的影响[3～5]，几何无关模型可以表示为：

式中，△P为双差伪距组合观测值；△准为双差载波相位组合观测值；△I为L1频点上的一阶双差电离层残差；β为相对于f1的一阶电离层延迟放大系数；ε为组合观测值的双差噪声；λ为组合观测值波长；△N为组合观测值双差模糊度；l,m,n,i,j,k为组合观测值的整数系数。

显然，采用几何无关模型求解模糊度的主要限制是电离层延迟和伪距噪声。

假定不同频率的双差载波相位观测值精度相等，且为：

由于BDSB3频点的码率是B1和B2频点的10倍，因此B3频点的伪距观测值精度优于B1和B2频点的伪距观测值[6]。则不同频点的双差伪距观测值精度可以表示为：

式中，n=1,2,…,10。

根据误差传播率可知，双差模糊度的精度为σ△N（以周为单位）：

根据多频线性组合观测值理论，筛选的超宽巷（EWL）、宽巷（WL）和窄巷（NL）载波相位观测值分别为：准(0,1,-1)、准(1,-1,0)和准(0,0,1)。

首先，固定超宽巷模糊度（EWL）：

式中，int[·]表示四舍五入取整。其次，固定宽巷模糊度（WL）：

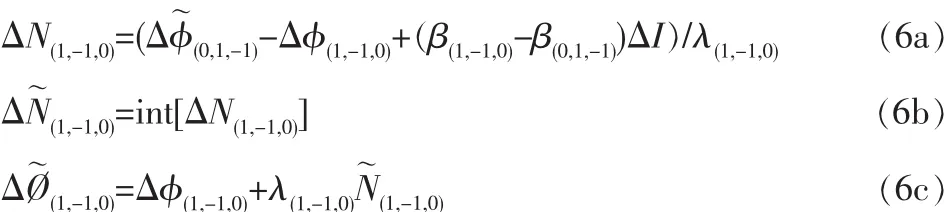
最后，固定窄巷模糊度（NL）：

对于传统的TCAR而言，窄巷模糊度由于其波长较短，易受双差电离层残差的影响。由于窄巷模糊度浮点解服从正态分布，其标准差可根据公式（4）求取，根据相关文献可求取窄巷模糊度的固定成功率[7]。当双差电离层残差大于7cm时，窄巷模糊度固定成功率几乎为0（见图1）。故可以考虑采用无几何无电离层模型，无几何无电离层模糊度解算的前两步与传统的TCAR没有差别，主要在于第三步窄巷模糊度的固定差别，无几何无电离层模糊度解算窄巷模糊度的固定可以表示为：

为了消除或减弱对流层误差、双差电离层残差、轨道误差等误差，组合系数a，必须满足以下条件：

此时，窄巷模糊度的观测噪声被放大，但是由于观测噪声服从零均值正态分布，故可以通过多个历元平滑，然后取整获取正确的窄巷模糊度值。

图1 双差电离层残差对单历元宽巷NL模糊度固定成功率的影响(σ△准=4mm,σ△P=60cm)

3 算例分析

文章采用TRIMBLENETR9型接收机采集了2组BDS/GPS三频基线实测数据，基线数据A与B共用一个基站。数据的概况见表1。为了更好地分析BDS与GPS三频模糊度解算的性能，统计了超宽巷、宽巷单历元模糊度固定成功率及窄巷模糊度的收敛速度和收敛值。试验中，设置截止高度角为25o，消除或减弱多路径的影响，并且考虑了不同参考卫星的影响。通过采用LAMBDA方法多历元连续搜索[8]，确定正确的模糊度值作为无几何无电离层模糊度解算的参考值。

从表2可以看出，以GEO卫星C01卫星为参考卫星，对数据A（零基线）、B（短基线），所有卫星对的超宽巷单历元模糊度固定成功率总是100%，数据A和数据B的宽巷单历元模糊度的成功率也超过99.99%。故BDS卫星超宽巷、宽巷模糊度可以实现单历元模糊度固定或者通过几个历元即可以平滑收敛到正确的模糊度值。以IGSO卫星为参考卫星，可以得到以GEO为参考卫星同样的结论（限于篇幅，未列出）。

表1 数据概况

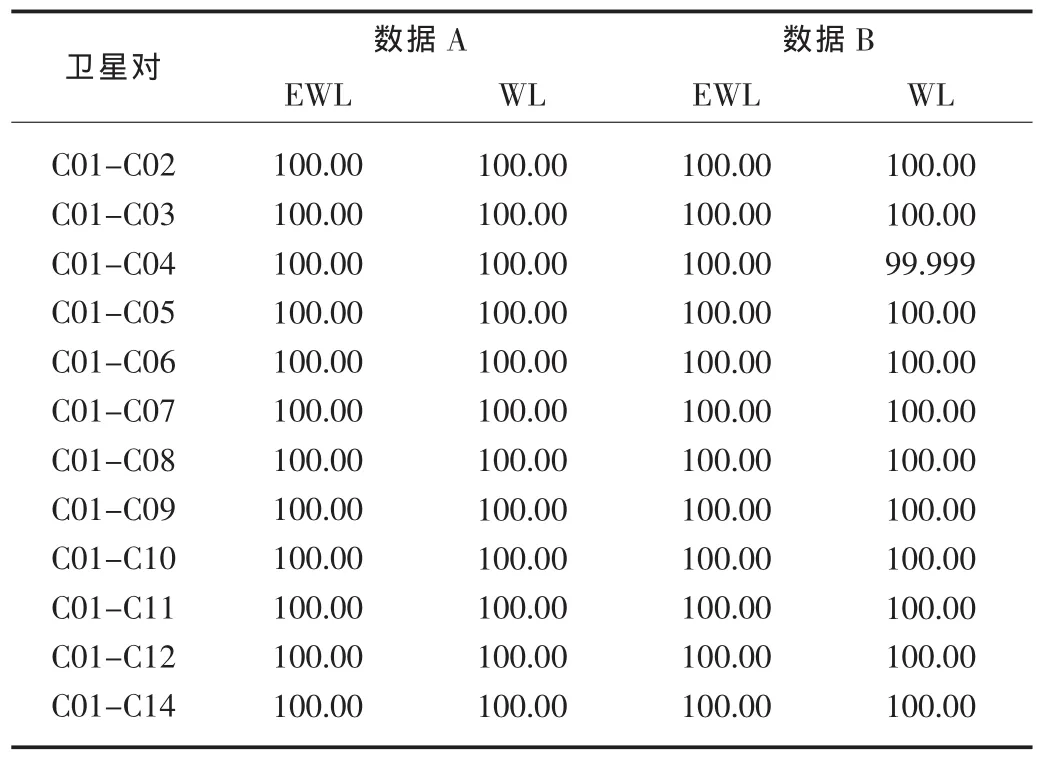
表2 数据A和BBDS卫星对超宽巷、宽巷单历元模糊度固定成功率

图2 数据A与数据B一天之内的GPS卫星跟踪情况，蓝色线条表示播发L5信号的卫星

从图2可以看出，数据A和数据B在截止高度角为5o时，一天之中可以观测到播发L5导航信号的卫星总共为8颗，但是在同一时段最多可以观测到6颗，最少仅为2颗。为了分析每颗播发L5信号的卫星，因此，可以以每3h为一段进行分析处理。分段分析卫星具体情况见表3。

表3 数据A和B不同时段的GPS卫星对

从表4可以看出，对数据A（零基线）、B（短基线），所有GPS卫星对的超宽巷及宽巷模糊度固定成功率总是保持99.999%以上。故GPS卫星对的超宽巷及宽巷也可以实现单历元模糊度快速固定。结合表2，可以得出：BDS与GPS采用无几何无电离层模糊度解算的超宽巷及宽巷可以实现单历元模糊度解算或几个历元平滑收敛为正确值。

从表5可以看出，对于数据A，数据处理时的截止高度角仅为25°，以C01-C02为代表，其窄巷模糊度通过几个历元可快速地收敛为正确值。根据表3的GPS卫星对的窄巷模糊度同样地可通过几个历元快速地收敛为正确值，在GPS数据处理时，截止高度角为5°，以便处理更多的历元数据。图3、图4描绘了数据A的BDS与GPS窄巷模糊度误差及收敛的时间序列 （限于篇幅，BDS以C01-C02为代表；GPS以G06-G24为代表）。

表5 数据ABDS卫星对不同历元数收敛的窄巷模糊度值

表6 数据AGPS卫星对不同历元数收敛的窄巷模糊度值

从图5可以看出，对于数据B，数据处理时的截止高度角仅为25°，以C01-C02卫星对为代表，其窄巷模糊度通过整个历元平滑也没有收敛为正确值。且出现了有周期性的波动情况，一个周期大概6h。这一现象可能是由载波相位多路径引起，可见载波相位多路径严重影响着窄巷模糊度的固定。以C06为参考卫星，也有类似的情况（限于篇幅，未绘出相应的图）。然而，根据表6的GPS卫星对所以窄巷模糊度可以通过多个历元平滑收敛为正确的模糊度值，数据处理时的截止高度角仅为5°，以便处理更多的历元数据（限于篇幅，仅绘出以G06-G24为代表的窄巷模糊度误差图），见图6。

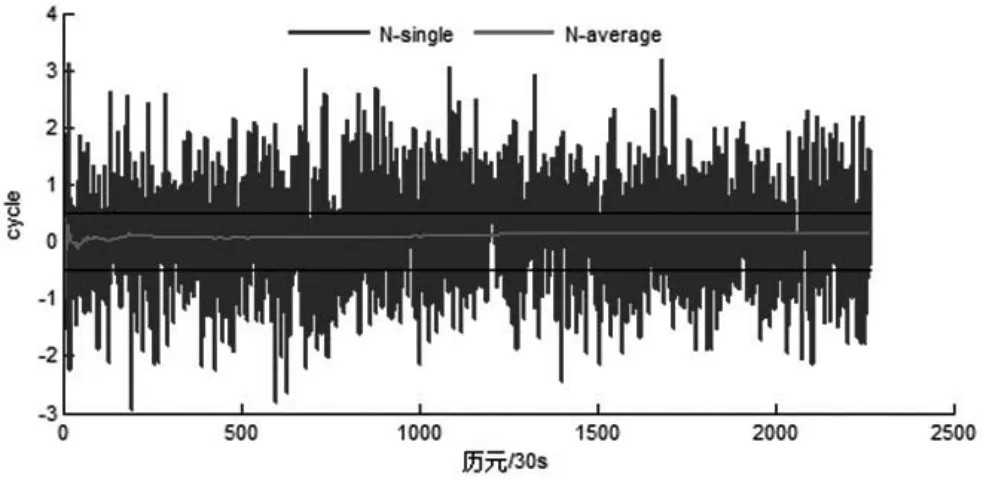
图3 数据ABDSC01-C02卫星对窄巷模糊度误差及其收敛的时间序列

图4 数据AGPSG06-G24卫星对窄巷模糊度误差及其收敛的时间序列

图5 数据BBDSC01-C02卫星对窄巷模糊度误差及其收敛的时间序列

图6 数据BGPSG06-G24卫星对窄巷模糊度误差及其收敛的时间序列

4 结论

文章采用的无几何无电离层模糊度解算方法，消除或减弱了对流层延迟、轨道误差及电离层延迟的影响，仅剩观测噪声及多路径的影响。通过二组实测数据对BDS与GPS的三频模糊度解算性能进行评估分析，可以得出以下结论：（1）对于超宽巷及宽巷模糊度，BDS与GPS都能够实现快速地固定，模糊度解算性能相当，不受基线长度的影响；（2）由于BDS的载波相位多路径比GPS很严重，其窄巷模糊度通过多历元平滑无法收敛为正确值，而GPS可以通过多个历元可平滑收敛为正确值。

【1】李金龙.BDS/GPS多频实时精密定位理论与算法[D].解放军信息工程大学，2014.

【2】LiB,FengY,ShenY.Threecarrierambiguityresolution:distanceindependentperformancedemonstratedusingsemi-generatedtriple frequencyGPSsignals[J].GPSSolut,2010,14(2):177-184.

【3】FengY.GNSSthreecarrierambiguityresolutionusingionosphere-reduced virtualsignals[J].JGeod,2008,82(12):847-862.

【4】李博峰.混合整数GNSS模型参数估计理论与方法[M].北京：测绘出版社，2014.

【5】Wangk,Rothacher.M.AmbiguityResolutionfortriple-frequencygeometryfreeandionosphere-freecombinationtestedwithrealdata[J].JGeod,2013, 87:539-553.

【6】TangW,DengCetal.Triple-frequencycarrierambiguityresolutionfor Beidounavigationsatellitesystem[J].GPSSolut,2013,18(3):335-344.

【7】TeunissenP.J.G.SuccessProbabilityofIntegerGPSAmbiguityRounding andBootstrapping[J].JournalofGeod,1998,72:606-612.

【8】Teunissen,P.J.L.Theleastsquaresambiguitydecorrelationadjustment:a methodforfastGPSintegerambiguityestimatio[J]n.JournalofGeod,1995, 70:65-82.

Performance Analysis of BDS and GPS Triple-frequency Ambiguity Resolution

LIULi-heng1,MANXiao-san2,YEXian-feng3
(1.TheFirstSurveyingandMappingInstituteofHunanProvince,HengYang421001，China; 2.ThePLAInformationEngineeringUniversity.Zhengzhou450001，China; 3.SchoolofEnergyEngineering,XiangtanUniversity,Xiangtan411100,China)

AsBDSandGPShave been broadcast triple-frequency, adopting geometry-free and ionosphere-free ambiguityresolution, this paper emphatically analyzesthe performance ofBDSandGPStriple-frequencyambiguityresolution.The two group ofBDS/GPS triple-frequencybaseline real data shows that the carrierphasemulti-pathdelayofBDSisseriousthanGPSasa result, the narrowlane ambiguityofBDScan't converge to correct valuesbymultiple epoch ,but the GPScan convergetothecorrectvaluebymultipleepoch.

geometry-freeandionosphere-free;BDS;narrowlaneambiguity

P2

A

1007-9467（2016）07-0230-04

2016-6-21

刘礼衡（1974～），男，湖南耒阳人，2008年评为测绘工程师，从事测绘数据处理研究，（电子信箱）hnliuliheng@163.com。