用Mason计算针板电极场强大小的适用性分析
张 凯,孙红梅
(1.国网辽宁省电力有限公司,辽宁 沈阳 110006;2.国网辽宁省电力有限公司检修公司,辽宁 沈阳 110006)
用Mason计算针板电极场强大小的适用性分析
张 凯1,孙红梅2
(1.国网辽宁省电力有限公司,辽宁 沈阳 110006;2.国网辽宁省电力有限公司检修公司,辽宁 沈阳 110006)
在进行XLPE电缆绝缘材料电树枝化试验时,广泛采用针板电极系统,研究了针电极的针尖形状及尖端曲率大小是否满足要求,并采用Mason公式计算针板电极系统最大场强是否适用、是否能正确反映针尖场强实际大小,结果证明试验用针电极尖端形态和尺寸均满足试验设计要求及Mason公式的适用条件,利用Mason计算试验用针板电极最大场强是可行的。
Mason;ANSYS;针板电极;电树枝化
随着城市和现代工业的迅速发展,XLPE电缆在我国城市电网中得到越来越广泛的应用[1-2],但同其他高分子聚合物绝缘材料一样,在电场的长期老化作用下,电树枝化已成为电缆绝缘失效的重要因素。
为解决由于电树枝化导致绝缘失效而影响电缆正常运行的问题,各国学者对绝缘材料电树枝化进行了研究[3-12],希望从不同的角度全面了解电缆绝缘材料电树枝化的特性。其研究试验手段之一是利用针板电极,通过施加不同形式的电压或将试样放置在不同温度下,进行电树枝的引发和生长特性的研究,目前已取得一定的成果[13-16]。
研究发现引发材料中电树枝化的原因很多,包括导体的凸起、毛刺、绝缘材料中的气隙和应力等,通常采用针板电极系统模拟上述因素进行试验研究。为方便研究结果对比,国内高校普遍采用曲率半径为5 μm、针板电极距离为2 mm的针板电极系统。在进行针板电极系统中针电极尖端电场强度计算时,均采用Mason公式进行估算。
在进行XLPE电缆绝缘直流电树枝化试验时,发现即使施加的直流电压值达到70 kV,利用Mason公式估算的最大场强为2 844.22 kV/mm,远高于材料的本征击穿电压800 kV/mm时,仍未能成功引发直流电树枝。在已有的研究结果基础上[17],为找出造成XLPE电缆绝缘材料在直流电压下电树枝化难以引发的直接原因,研究是否由于Mason公式计算试验条件下针尖场强的误差增大及是否由于针板电极系统中针电极尖端形态不符合要求而导致试验结果的出现。
目前已有文献对用Mason公式计算尖电极场强进行误差研究[18]。本文采用ANSYS有限元仿真软件,对Mason公式是否能用来计算设定试验条件下针板电极系统电场强度大小进行研究,研究Mason公式是否可以用于估算试验用针板电极的最大场强。同时利用Matlab对实际针电极的形状和尖端曲率半径进行提取,研究试验所用针电极形状和曲率半径是否满足试验设定条件及Mason公式使用条件的要求。
1 Mason和ANSYS计算结果对比
1.1 Mason公式
J.H.Mason在1951年提出针板电极系统最大场强的近似计算公式[19]。我国倪光正等从理论出发,详细推导了标准双曲面最大场强计算过程[20],并最终得到了Mason公式在长旋转椭球坐标系中的电位、尖端最大场强的表达式及直角坐标系中尖端最大场强的表达式。推导前提是为标准旋转双曲面的电位函数建立数学模型,并归结为如下的边值问题:
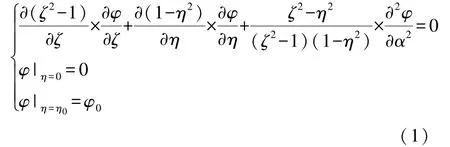
通过进一步推导,得出电位函数的解为

针尖最大场强表达式为

式中 φ——电位函数;
η——长旋转椭球坐标;
φ0——电极间的外施电压;
Emax——针尖最大场强;
h——针尖到平面的距离。
考虑到实际针电极表面不完全符合双曲面要求,但在计算中可将针尖端部位近似成曲率为R的双曲面,考虑到R≪h,可将式(3)简化得到Mason公式:

式中 R——曲率半径;
H——针板电极间距;
U0——试验所加电压。
由上述推导过程可知,Mason公式可适用于尖端轮廓为标准双曲面的针板电极系统。
1.2 用ANSYS计算及建模验证
为实现ANSYS软件进行后续计算仿真工作,首先验证ANSYS建模、加载荷及计算的正确性,即用ANSYS对标准旋转双曲面针板电极系统场强分布进行计算和仿真,并将仿真所得结果同Mason公式计算结果进行比较。
为使计算更具有实用性,能和实际情况相结合,在ANSYS建模时,取针尖曲率半径R=5 μm,针板电极间距d=2 mm。同时为了建模简单,优化资源利用,将实际中的试样进行简化,如图1所示。针电极模型为其尖端部位,板电极模型为相对针尖尺寸较大的平板,电极间区域填充的介质为XLPE,分别在针电极与板电极所在区域加电压载荷后进行有限元计算。
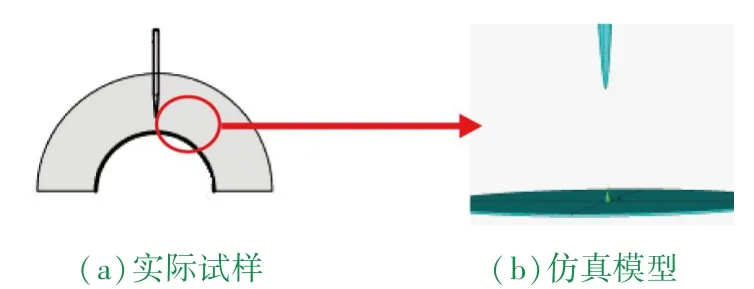
图1 ANSYS建模简化
针电极建模时,采用轴对称结构特有的简化算法,即将所用单元的关键项设为轴对称方式,然后建立1/4体积截面的针尖模型进行仿真计算。针尖是用标准双曲方程绘制而成,如式(5)所示:


利用式(6)对标准双曲形状的针电极针尖进行绘制,然后完善模型,包括绘制平板电极、半圆形介质模型和圆环形的无限远场,最终模型如图2所示。
在进行计算时,选择的分析类型为静态电场分析,单元类型为PLANE121,开启轴对称选项,为了使计算结果更具有实用性,所加载荷为试验所得的XLPE电缆50%绝缘雷电击穿电压为35 kV,选用ANSYS默认求解器,求解结果如图3所示。
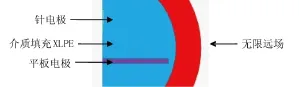
图2 ANSYS建模
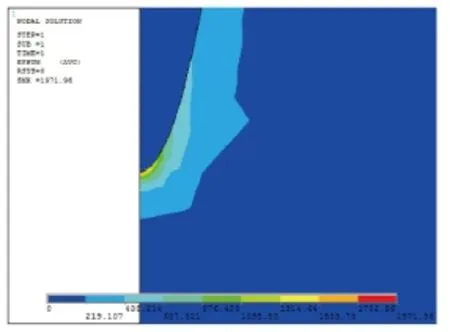
图3 双曲针尖仿真结果
由图3可见,双曲针板电极系统中,针尖曲率R=5 μm,针板距离d=2 mm,施加电压U0=35 kV时,仿真得出最大场强分布在针尖处,仿真计算结果为Emax=1 971.96 kV/mm。在相同的条件下,即针板距离d=2 mm,曲率半径R=5 μm,施加的电压U0=35 kV,代入Mason公式进行计算,Emax=1 897.43 kV/mm,结果相对误差为3.92%,可以认为Mason公式和ANSYS计算结果是相同的。由于Mason公式是通过纯理论推导得出,完全适用于标准双曲面,其计算结果能反映电压值作用在针电极尖端处场强的大小,对比仿真结果可知,本文所采用的ANSYS建模、加载荷及计算方法切实可行,可用于计算针板电极下针尖的最大场强。
2 实际针尖模拟
2.1 提取实际针电极形态
为确定用Mason公式估算实际针板电极针尖场强的合理性,用ANSYS对XLPE电树枝化试验所用针电极尖端进行仿真计算。在ANSYS中建立的实际针尖模型数据是通过Matlab对针电极尖端图像形状提取得到的,Matlab中针电极尖端图像形状提取步骤如图4所示。
得到针尖轮廓点的坐标后,在Matlab软件中选取拟合结果较好的拟合函数进行拟合,经过尝试发现用8级Fourier函数进行拟合较合理。拟合函数为
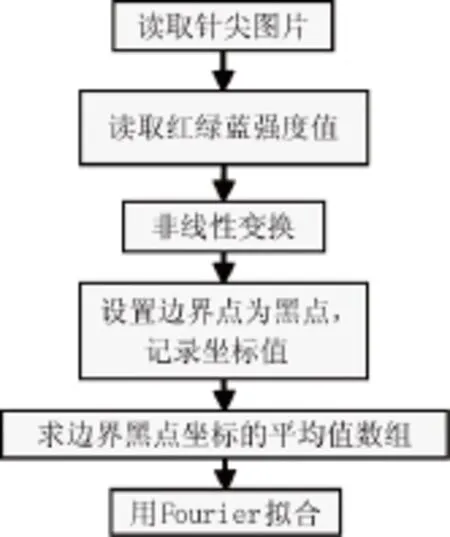
图4 实际针尖拟合流程
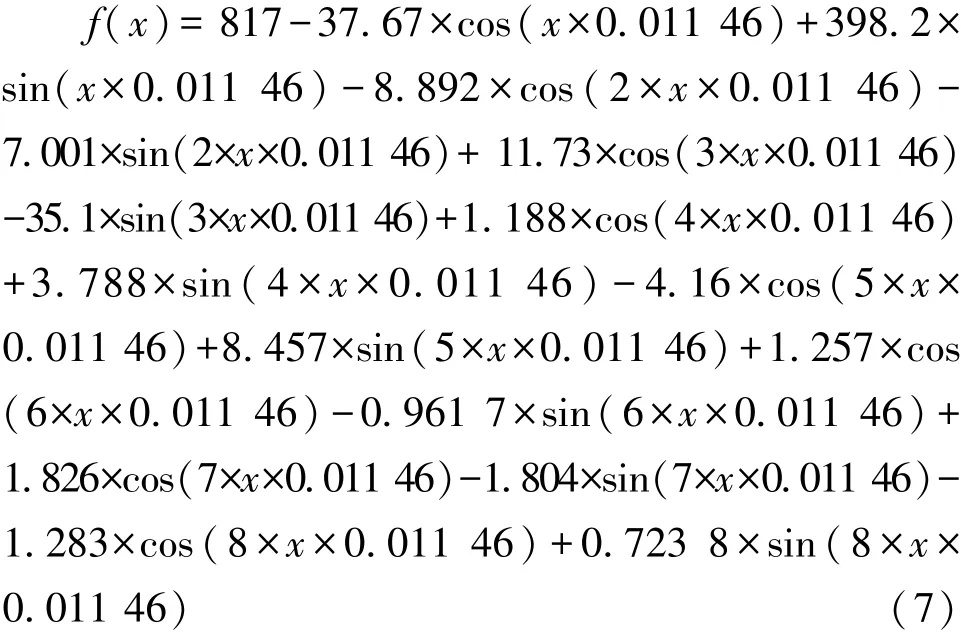
将拟合所得结果与原数据点进行比较,标准方差为2.05,结果如图5所示。根据曲率半径的定义,求取拟合后的针电极曲线在针尖处的曲率半径R=6.988 μm,基于拟合过程中的误差,由图5(c)可以看出,拟合曲线与原轮廓线相比,曲率相对较大,故认为实际针尖处的曲率半径R≈5 μm。
2.2 实际针电极和标准双曲线形态对比
针尖轮廓曲线和标准双曲线对比如图6所示,在相同曲率半径下,实际针尖形状不能完全符合双曲线的形状,但在尖端局部有很好的重合,计算针电极尖端最大场强时,由于针尖电极尖端局部形状满足标准双曲线要求,采用Mason公式进行针电极最大场强的估算是可行的。
2.3 用ANSYS计算实际针电极场强大小
用式(7)的拟合函数,绘制ANSYS模型中的针电极,进行仿真计算,所涉及的建模、加载荷和计算流程与上述标准双曲模型仿真计算过程一致,结果如图7所示。从仿真结果看,实际针电极的最大场强分布在针尖处,且针尖最大场强Emax=1 486.05 kV/mm。该场强值是在只考虑施加电压作用下,针电极尖端处的实际场强大小。
用Mason公式估算实际场强值,将R=6.988 μm,d=2 mm代入式(4),得Emax=1 422.11 kV/mm。将该值与ANSYS仿真计算结果Emax=1 486.05 kV/mm进行比较,两者相差4.49%。从而可以看出,用Mason公式估算电树枝化试验用针板电极系统的场强时,其估算结果能切实反映所施加电压作用在针电极尖端处产生场强的大小。
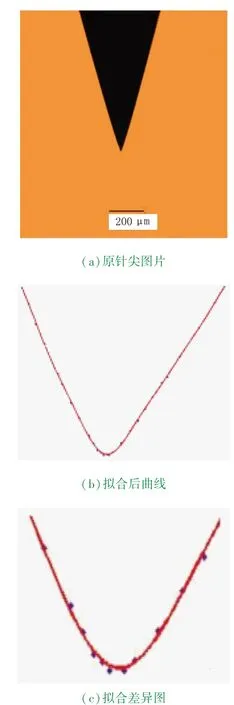
图5 实际针尖提取过程

图6 轮廓对比
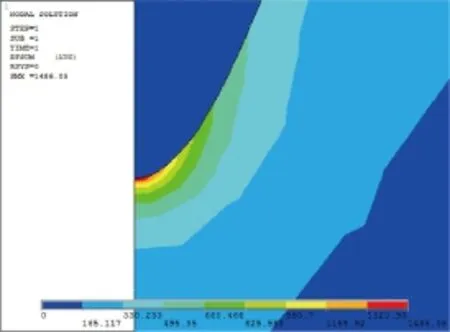
图7 实际针尖的ANSYS仿真结果
3 结论
利用ANSYS仿真分析了标准双曲面和实际针尖形状曲线的最大场强,并和Mason计算结果比较,发现ANSYS仿真实际针尖的结果同Mason计算结果相近,因此,可用Mason公式对实际使用的针电极尖端处的最大场强进行估算,当曲率半径为5 μm,针板距离为2 mm时,用Mason计算针电极最大场强的大小所引起的误差在可接受范围内。试验结果同时说明,实际使用的针电极尖端不满足标准双曲面的要求,但在尖端局部能与标准双曲面很切合,从而满足了Mason计算条件。结果还说明在实际电树枝试验中[14],当在试样的针电极上施加35 kV直流电压时,针电极尖端处场强Emax可高达1 897.43 kV/mm,此值远远高于XLPE电缆绝缘材料的击穿场强800 kV/mm,但实际中并没有能够成功引发电树枝,这证明正是由于同极性空间电荷的作用削弱了针尖处场强,使试样没有引发电树枝。
[1]姜小兵.XLPE电缆线芯温度计算方法研究[J].东北电力技术,2014,35(3):1-3.
[2]金 鑫,李书硕,王东烨.交联电缆0.1 Hz试验方法研究[J].东北电力技术,2009,30(9):5-7.
[3]FH Kreuger.Partial discharge detection in high-voltage equipment[M].London:Butterworths,1989.
[4]LA Dissado,JC Fothergill.Electrical degradation and breakdown in polymers[M].London:Peter Peregrinus,1992.
[5]J Densley.Ageing mechanisms and diagnostics for power cables-an overview[J].IEEE Electrical Insulation Magazine,2001,17(1):14-22.
[6]J Densley,T Kalickil,Z Nadolnf.Characteristics of PD pulses in electrical trees and interfaces inextruded cables[J].IEEE Trans. Dielectrics and Electrical Insulation,2001,8(1):48-57.
[7]Fukuda T.Technological progress in High voltage XLPE power cable in Japan[J].Electrical Insulation Magazine,1998,4(6):15-20.
[8]Muller K B,Tretow U,Dellby B,et al.XLPE cable Technology for operating voltage of 245 kV and above[J].IEEE Transaction on Power Delivery,1990,5(4):1 660-1 668.
[9]李盛涛,郑晓泉.聚合物电树枝化[M].北京:机械工业出版社,2006.
[10]陈仕军.不同条件下交联聚乙烯电缆电树枝生长特性研究[D].重庆:重庆大学,2009.
[11]石 峰.交联聚乙烯电缆耐压试验方法[J].东北电力技术,2010,31(1):47-49.
[12]张秀阁,贺景亮,王洪新,等.工频电压下XLPE绝缘的电树枝老化实验研究[J].高电压技术,1998,24(4):57-58.
[13]郑晓泉,G CHEN.XLPE电缆绝缘中的电树枝种类及其影响因素[J].电工电能新技术,2003,22(4):21-24.
[14]刘 英,曹晓龙.直流电压下交联聚乙烯电缆绝缘中电树枝的生长特性研究[J].西安交通大学学报,2014,48(4):41-46.
[15]鲍明晖,尹小根.高频电压下交联聚乙烯中电树枝的形态特性[J].中国电机工程学报,2011,31(34):184-191.
[16]陈向荣,徐 阳.高温下110 kV交联聚乙烯电缆电树枝生长及局部放电特性[J].高电压技术,2012,38(3):645-654.
[17]Liu ying,Cao xiaolong.Electrical tree initiation in XLPE cable insulation by application of DC and impulse voltage,IEEE Transactions on Dielectrics and Electrical Insulation,2013,20(5):1 691-1 698.
[18]文康珍,文元芳,端木林楠,等.尖电极静电场ANSYS解的误差[J].电瓷避雷器,2009,43(2):14-16.
[19]J.H.Mason:The Deterioration and Breakdown of Dielectrics Resulting from Internal Discharges,PIEE,1951,Vol98.Pt I.
[20]倪光正,吴 炯.Mason公式的导出及其在树枝放电研究中的应用[J].西安交通大学学报,1984,18(4):87-93.
Suitability Analysis on Needle Plate Electrode Field Strength Based on Mason Calculation
ZHANG Kai1,SUN Hong⁃mei2
(1.State Grid Liaoning Electric Power Co.,Ltd.,Shenyang,Liaoning 110006,China;2.Maintenance Company of State Grid Liaoning Electric Power Co.,Ltd.,Shenyang,Liaoning 110006,China)
Learners commonly use the needle plate electrode system when studying the properties of the electrical tree in XLPE cable insulation.This paper studies that whether the profile of the needle electrode tip meets the hyperbolic shape or the curvature of needle electrode tip meets the requirements.This paper also studies that whether the theoretical analysis of the field strength in the needle plate electrode system with Mason formula can correctly describe the field strength at needle electrode tip in the experiment.The results show that the shape and size of the needle electrode tip can meet the requirements of design of experiment.The Mason formula can be used to calculate maximum field strength of the needle plate electrode system in the experiment.
Mason;ANSYS;Needle plate electrode;Electrical tree
TM74
A
1004-7913(2016)06-0027-04
张 凯(1985—),男,硕士,工程师,从事电力系统运行工作。
2016-03-20)

