高速铁路网络能力计算研究

张嘉敏，张嘉锐

（1.山东科技大学 交通学院，青岛 266590；2.济南铁路局 青岛机务段，青岛 266041）

高速铁路网络能力计算研究

张嘉敏1，张嘉锐2

（1.山东科技大学 交通学院，青岛 266590；2.济南铁路局 青岛机务段，青岛 266041）

充分考虑高速铁路网络作为多级递阶控制系统的复杂性和对旅客运输服务质量的要求，构建基于时段特定场景的高速铁路列车服务与需求意向集合（t@n-tsdis，train service-demand intention set at network），定义以完成这个集合所需基础设施占用时间为网络能力的衡量标准。提出了两阶段的优化计算方法，并提出多目标优化改进的Pareto（1+1）— PAES算法流程，采用交互式滚动优化策略处理整数约束条件、模糊逻辑罚函数法处理连续实数约束条件、Pareto存档进化策略求解多目标优化问题。以某高速铁路网络为例进行能力计算，验证了模型与算法的有效性。

高速铁路；网络能力；列车径路规划；多目标优化；Pareto存档进化策略

铁路能力具有动态性特征，其大小与运输需求、使用方式有关。从运输组织管理体制上看，铁路网运输系统是一个多级递阶控制的大系统。UIC406能力手册将列车数、平均速度、稳定性及异质性定义为能力使用的核心元素，将能力消耗参数定义为关于能力使用的平衡；文献[1]提出了能力的金字塔式平衡关系图。铁路能力影响因素众多，大多体现在时间维度。文献[2]构建基于时段特定场景的列车服务与需求意向集合（t@n-tsdis，train service-demand intention set at network），定义以完成列车服务与需求意向集合所需的基础设施占用时间作为衡量高速铁路能力的新标准，分析了网络化条件下轨道交通系统的能力。

铁路能力计算的方法可归结为分析方法、优化方法、仿真方法等，基于高速铁路网络作为一个多级递阶控制系统的复杂性及其对运输服务质量的要求，结合能力的动态性和不确定性特征，本文将高速铁路网络的能力定义为在最小化异质性、最大化可靠性的同时，最小化完成列车在高速铁路网络的列车服务与需求意向集合（t@n-tsdis）所需基础设施占用时间，即运行时间，分两个阶段计算高速铁路的网络能力：（1）列车径路规划，将高速铁路物理网的能力转化为由运行径路构成的有向服务网的能力；（2）多目标优化，计算综合平衡条件下考虑一定服务质量的网络能力，从而在服务可靠度与最大物理能力之间找到经济优化的能力平衡点。

1 列车径路规划

在列车径路规划阶段，对于给定的高速铁路网络，确定必开起讫点OD，应用图论求解必开起讫点OD对间的最短路径，再进行径路微调，使网络图中的每个节点至少被一条径路覆盖。列车径路规划算法为：

（1）根据经济总量、人口规模、地理位置、政治地位等因素划分车站节点等级，确定必开起讫点OD，必开起讫点间应至少开行一次相应等级的旅客列车。

（2）运用图论Dijkstra算法求解高速铁路网络图中必开起讫点间的最短路径，作为基本列车运行径路集。

（3）以每个节点至少被一条列车径路覆盖为准则，判别基本列车运行径路集是否覆盖所有车站节点，如果是，转（5），否则转（4）。

（4）对基本运行径路进行K短路调整，构建扩展运行径路。定义列车运行径路的模为其径路里程长度，根据模从小到大对列车基本运行径路排序，排序设为{a,b,c,...}。

选取模最小的基本运行径路a，对其进行K短路调整，构建扩展运行径路，判别当前列车运行径路集能否覆盖所有车站节点，如果能，转（5），否则，对基本运行径路b进行K短路调整，再判别当前列车运行径路集能否覆盖所有车站节点，如此依序循环往复调整，直至当前列车运行径路能覆盖所有车站节点。

（5）列车径路规划完毕。

2 多目标优化模型

令S为高速铁路网络车站的集合，Q为区间集，q代表区间，s为在列车运行方向进入区间q的车站，s∈S。tj为列车j的运行径路，T代表列车运行径路集合，tj∈T。ejq为列车j进入区间q的时刻，ljq为列车j离开区间q的时刻，rjq为列车j在区间q的运行时间， hjq为在区间列车j与j-1的最小间隔时间，为列车j与j-1到达车站s的间隔时间 。

aijq为进入区间q的列车i与j的最小间隔时间。xijq为0-1变量：

高速铁路列车的服务质量可从异质性、可靠性及运行时间几方面考量。文献［3］提出用最小间隔时间倒数的和表示不同种类列车区间组合的异质性，用到达间隔时间倒数的和表示不同类型列车组合在车站的异质性；异质性会增加列车运行过程中延误传播的可能性，降低运行图的稳定性。铁路网系统运输能力可靠性与铁路网系统有效使用能力直接相关，可以通过列车间隔时间的合理设置提高运行的可靠性。文献 [4]提出并证明了在混合交通流条件下列车运行时间的定理。根据高速铁路网络能力的定义，考虑一定服务质量的综合平衡条件下，高速铁路网络能力计算的多目标优化模型为：

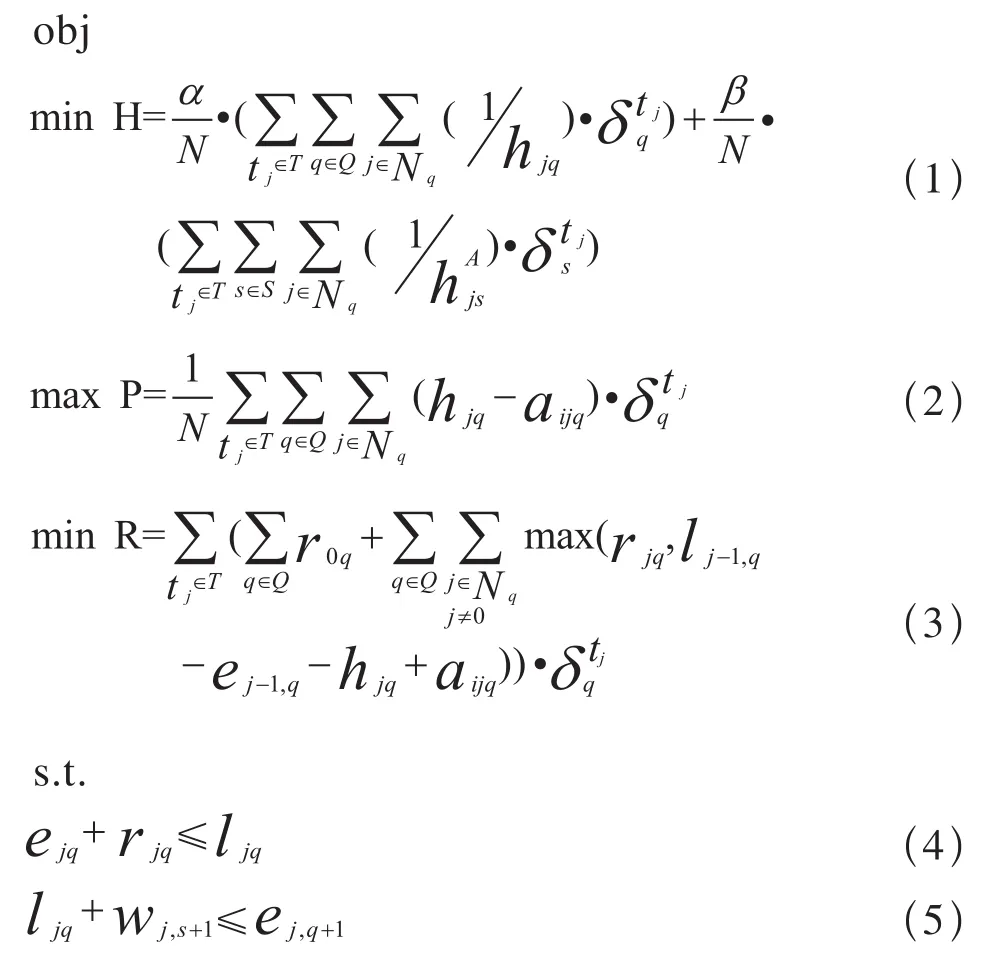
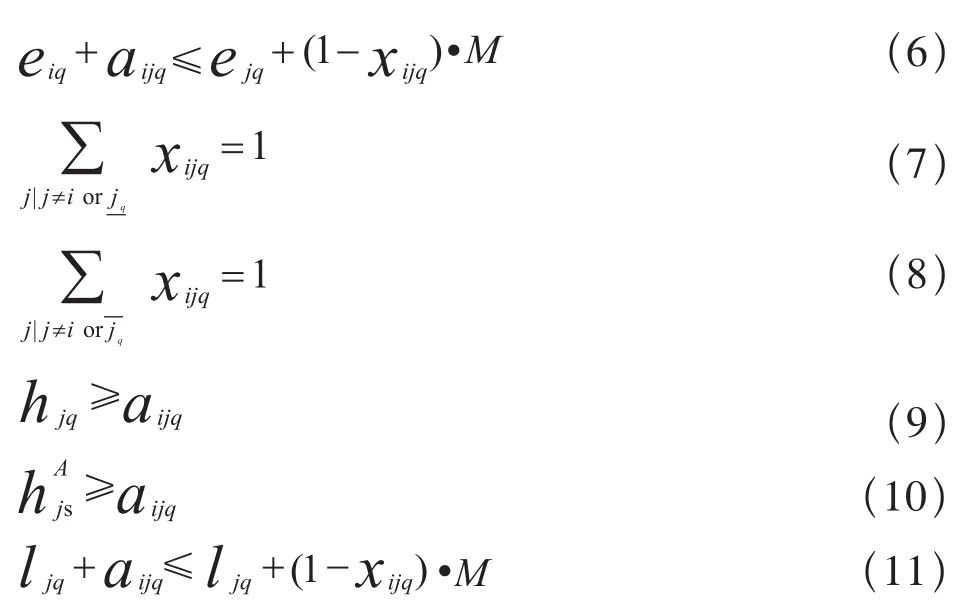
模型中，式（1）～式（3）为目标函数，其中，式（1）为最小化异质性，式（2）为最大化可靠性，式（3）为最小化运行时间。式（4）～式（11）为约束条件，其中，式（4）表示列车离开区间的时刻与其进入区间的时刻之差不小于其在区间运行时间；式（5）表示列车进入区间的时刻与其离开前一个区间的时刻不小于其在车站的作业时间；式（6）表示两个相邻的列车进入同一个区间的时间之差不小于列车控制系统所规定的最小安全间隔时间；式（7）表示除第一列列车外，每列列车有且只有唯一一个直接前驱；式（8）表示除最后一列列车外，每一列列车有且只有唯一一个直接后继；式（9）表示列车在区间的最小间隔时间不小于列车控制系统所规定的最小安全间隔时间；式（10）表示列车在车站的到达间隔时间不小于列车控制系统所规定的最小安全间隔时间；式（11）表示两个相邻的列车离开同一个区间的时间之差不小于列车控制系统所规定的最小安全间隔时间。

3 模型求解算法

3.1 模型预处理

3.1.1 目标函数标准化

对模型的目标函数标准化（最小化）处理：

则标准化后的目标向量为：

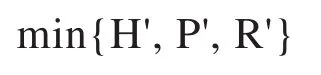
3.1.2 整数0—1约束部分的处理

根据文献[5]对运行图结构的分析，将车站视为缓冲库存，将区间视为加工设备，以阶段均衡模式为基础，采用just-in-case策略，对整数0-1规划约束采取交互式滚动优化处理方法，如图1所示。

图1 以车站—区间为单元的 just-in-case交互式滚动优化

3.1.3 连续实数约束条件的处理

对实数型约束条件依据gi(v)≥0（i=1,…,6）形式标准化处理，应用模糊逻辑罚函数法处理转化后的实数约束条件。令tvi表示解v对于约束i的冲突程度，且有：

令Zi表示第i个不可行域的容忍阈值（置各区域的容忍阈值Zi分别为0.001， 0.01， 0.02， 0.5， 1.0，5.0， 10.0， 15.0， 25.0， 35)，yv为解v的模糊罚函数（代表在非可行域中解违反约束的程度），将整个搜索空间划分为10个区域。

Zone 1 为可行域，惩罚项yv=0，此时有：

max(tv1,…,tvL)≤Zi；

Zone i，i=2～9， 为惩罚空间，惩罚项yv=i，此时有：

Zi–1＜max(tv1,…,tvL)≤Zi；

Zone 10为拒绝空间，惩罚项yv=100，此时有：

Z10＜max(tv1,…,tvL)。

对于任意解v，根据模糊罚函数法，转化的目标函数分别为：

F1=H'+yv

F2=P'+yv

F3=R'+yv

至此，应用模糊—逻辑罚函数将带约束的多目标规划问题转换为无约束的多目标优化问题：

min{F1,F2,F3}

3.2 Pareto存档进化策略与交互法求解多目标优化问题

以车站—区间为单元滚动优化，在每一单元采用改进的Pareto（1+1）—PAES［6］存档进化策略与交互法，求解转换后的无约束多目标优化问题，基本流程如图2所示。

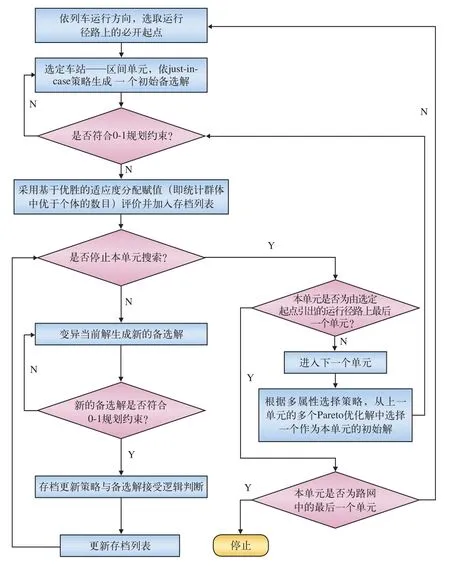
图2 多目标优化改进的Pareto（1+1）—PAES算法流程

将t@n-tsdis中的列车视为列车群，采用justin-case策略生成初始解。在改进的Pareto（1+1）—PAES存档策略中维持当前的Pareto最优解，在每一次迭代中依据各约束条件违反情况与当前目标值优化程度进行对当前解的取舍，并从更新后存档列表中选择一个产生变异解。PAES评估函数基于支配关系进行个体评价，改进的Pareto（1+1）—PAES亦采取基于优胜关系的适应度赋值（即统计群体中优于个体的数目，设某个体i被群体占优的个数为di，取di的倒数作为个体i的适应度），改进的Pareto（1+1）—PAES存档更新与当前解接受逻辑如图3所示。

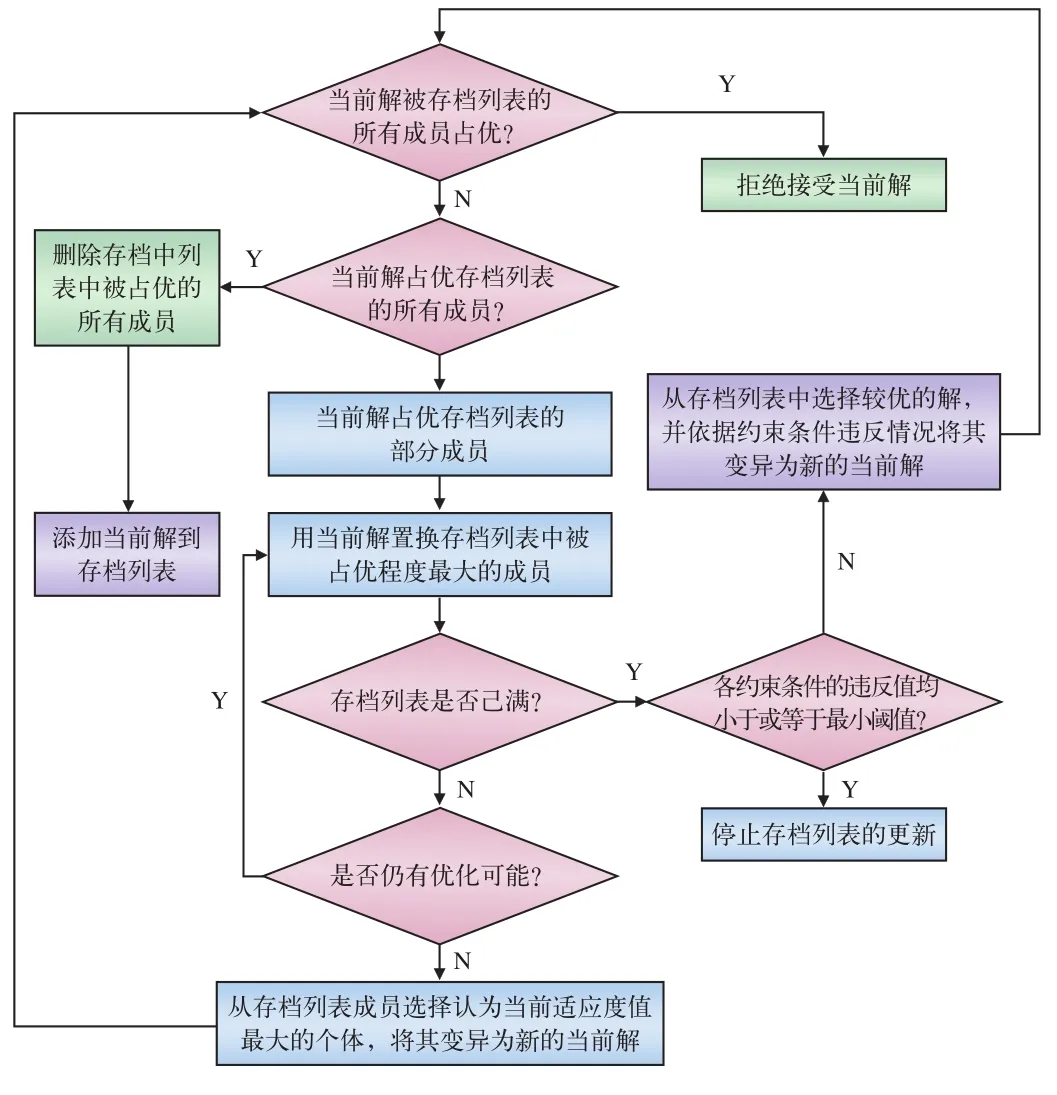
图3 改进的(1+1)-PAES存档列表更新策略与当前解接受逻辑

4 算例应用

某小型高速铁路网络如图4所示。图4中，数字代表相邻站间距离，字母代表车站节点，其中 ，A、B、C、D为必开起讫点，B、C为一级节点，A、D、F、G为二级节点，E、H为三级节点。

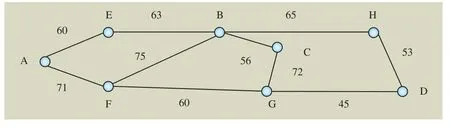
图4 某高速铁路网络图

根据列车径路规划算法流程，列车径路规划如表1所示。

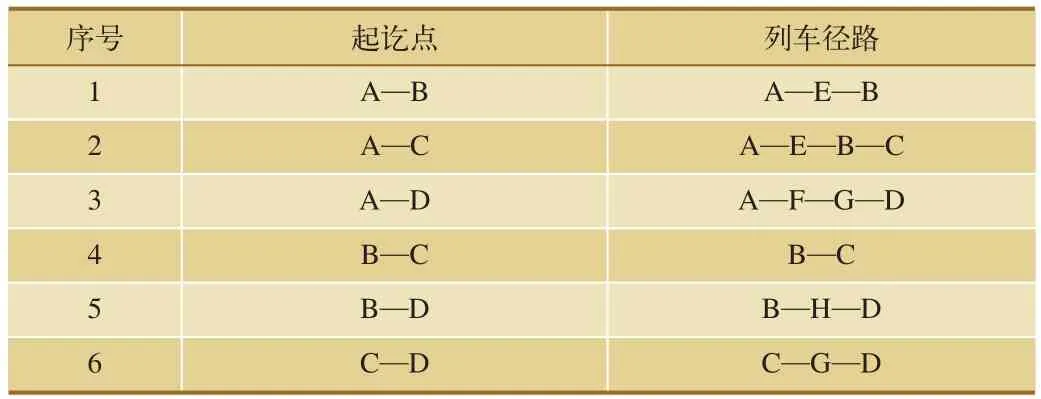
表1 列车径路规划

构造某高峰时段高速铁路网络的t@n-tsdis任务列表如表2所示。

表2 某高峰时段高速铁路网络 t@n-tsdis任务列表

根据提出的模型求解算法，运用.net平台环境下的C#语言编程，对高速铁路网络能力计算模型优化求解的结果如表3 所示。根据模型优化结果，完成高速铁路列车在网络的服务—需求意向集合（t@ n-tsdis）需占用基础设施的总时间为569.96 min ，实现这个目标的异质性全网合计为2.039 180 505，全网平均为0.254 897 563，可靠性全网合计为0.872 543 069，全网平均为0.096 949 23。在所有车站—区间单元中，异质性最高值为0.419 718 593 140 599，出现在G—D单元，其对应的可靠性为0.015 151 515 151 515 2，G—D单元是整个网络系统的能力薄弱部分，在实际运营中需要加强对G—D单元的列车运行组织，以实现网络系统的能力加强。

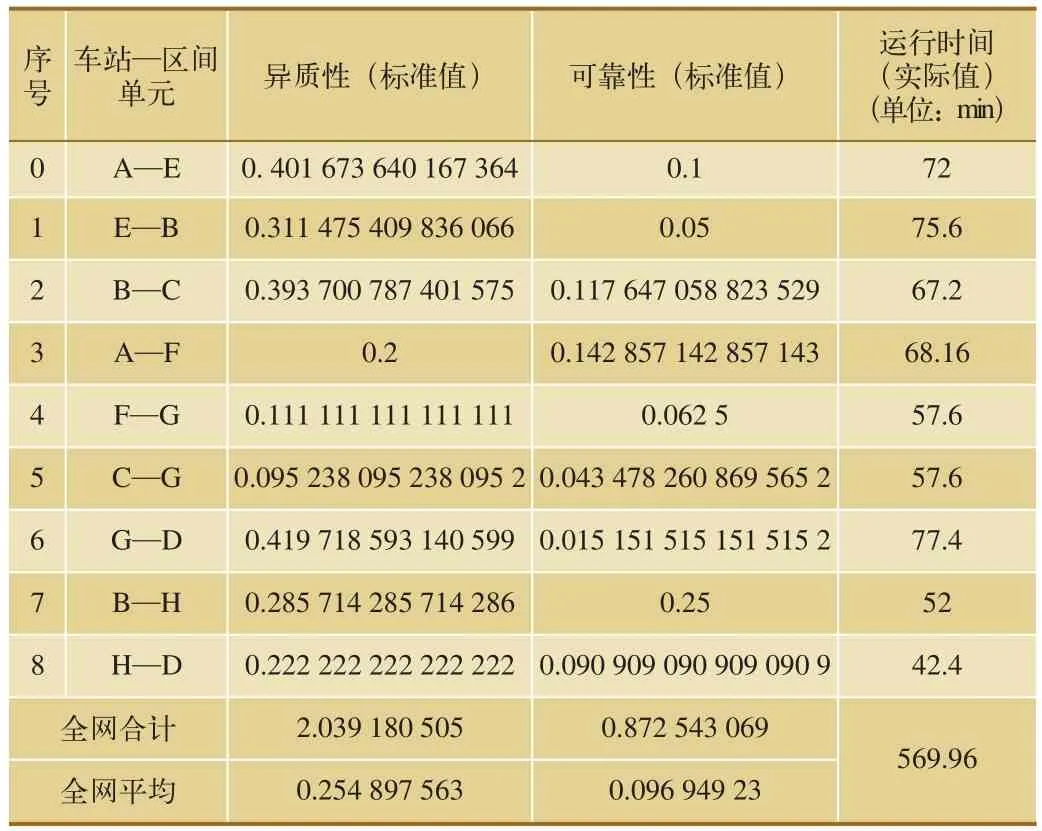
表3 高速铁路网络能力计算优化目标结果

5 结束语

高速铁路的运输组织模式从传统的以运能管理为中心转变为以旅客服务为中心，基于高速铁路网络作为多级递阶控制系统的复杂性和对旅客运输服务质量的要求，本文定义了高速铁路网络能力的衡量标准，以完成高速铁路列车在网络的列车服务与需求意向集合（t@n-tsdis）所需要占用的基础设施时间为网络能力的衡量标准，提出高速铁路网络能力计算的两阶段方法，以某高速铁路网络为例进行了算例应用。能力计算的一个主要意义在于指导实际列车运营服务，本文提出的高速铁路网络能力两阶段计算方法，可以在路径规划的基础上，通过多目标优化，计算得到考虑一定服务质量的综合平衡条件下的路网能力，能够更充分地把握铁路能力的动态性特征，更接近高速铁路网络列车运行组织的实际。

[1]Landex,A.Methods to estimate railway capacity and passenger delay[D].Denmark:Technical University of Denmark,2008.

[2]张嘉敏.高速铁路能力计算与评估之理论与方法研究[D].北京：北京交通大学，2012.

[3]Michiel J.C.M.Vromans.Reliability and heterogeneity of railway services[J].European Journal of Operational Research,2006:647–665.

[4]Tijs Huisman,Richard J.Boucherie.Running times on railway sections with heterogeneous train traffic[J].Transportation Research Part B ,2001 (35):271-292.

[5]Jiamin Zhang,Jun Liu.Analysis on Comprehensive Balance of Train Operation Plan for High Speed Railway under Mixed Traffic Condition[C].International Conference on Intelligent Rail Transportation，2011:397 – 401.

[6]Joshua D.Knowles,David W.Corne.Approximating the Nondominated Front Using the Pareto Archived Evolution Strategy[J].Evolutionary Computation， 1999，7(1):1-24.

责任编辑 王 浩

Calculation of network capacity for high-speed railway

ZHANG Jiamin1,ZHANG Jiarui2
( 1.College of Transportation,Shandong University of Science and Technology, Qingdao 266590,China;2.Qingdao Locomotive Depot,Jinan Railway Administration,Qingdao 266041,China)

Taking full account of the high speed railway network as the complexity of the multilevel hierarchical control system and requirements for the quality of passenger transport service,this article set up the high-speed train service-demand intention set at railway network according to the specifc scenario of the period ( train service-demand intention set at network,abbreviated as t@n-tsdis),and then took the occupation time of the infrastructures needed to fulfll the set as the criteria to measure the network capacity,proposed the two stage optimization calculation method.On solving the model,the article proposed improved (1+1)-PAES Algorithm fow for multi-objective optimization,and took the interactive-rolling strategy to tackle the integer constraints,the fuzzy-logic penalty function to tackle the real constraints,and the Pareto archived evolution strategy to solving multi-objective optimization problems.The model and the Algorithm were applied to a high speed railway network for case study,the validity of the model and the Algorithm was verifed.

high-speed railway;network capacity;train path planning;multi-objective optimization;Pareto archived evolution strategy

U238：U293：TP39

A

1005-8451（2016）08-0016-05

2016-02-17

山东科技大学人才引进科研启动基金项目（2014RCJJ025）。

张嘉敏，讲师；张嘉锐，工程师。