对40 Hz听觉稳态反应应用线性叠加条件的评估

林 霖 谭小丹 王 涛

(南方医科大学生物医学工程学院，广州 510515)

对40 Hz听觉稳态反应应用线性叠加条件的评估

林 霖 谭小丹 王 涛*

(南方医科大学生物医学工程学院，广州 510515)

多刺激率稳态平均去卷积技术(MSAD)是一种基于线性叠加模型重建高刺激率下瞬态反应的新方法，这种模型在应用时要求刺激率的改变对稳态或瞬态反应不产生实质性影响。记录20位受试者在8组刺激率(平均约为40 Hz)下稳态反应，采用MSAD技术估计其构成的瞬态反应。通过对比以此合成稳态反应与所记录的稳态反应之间的差别，评估MSAD模型的有效性。结果发现，两者的V-Na峰峰值和V波潜伏期基本一致；在36.8和39.1 Hz刺激率下，合成稳态反应与记录稳态反应之间不存在统计学差异，在36.8 Hz下两者相对误差最小，为7.95%。上述结果表明，刺激率在适当范围内的变化对诱发反应的影响较小，MSAD计算条件成立。

听觉稳态反应；多刺激率稳态平均去卷积；线性叠加理论

引言

听觉诱发电位(auditory evoked potential, AEP)是人类的听觉系统受到声音刺激后，在头皮上记录的一系列电位变化，反映了从耳蜗到听觉神经中枢电生理活动情况。由于记录到的AEP十分微弱，临床上通常采用短声或短音等组成的脉冲形式刺激序列反复刺激听觉系统，通过平均方法抑制随机型噪声，得到一个持续时间短暂的瞬态AEP。如果采用刺激间隔(stimulus onset asynchrony，SOA)小于瞬态反应时长的周期性序列，AEP表现出和刺激率相同的节律波形，称之为听觉稳态反应(auditory steady state response, ASSR)[1]。由于ASSR在40 Hz刺激率条件下，幅度明显增大，有学者提出稳态反应是由于若干个瞬态反应前后重叠所引起[2]。这个ASSR的产生过程被称为线性叠加理论。然而，采用常规瞬态反应预测稳态反应时，由于神经系统对重复刺激产生的适应性机制往往使得实际测量结果存在显著差别。因此，在快速刺激方式下，恢复重叠的瞬态反应不仅有助于验证叠加理论，还可以用于探索神经系统的适应性现象及其对AEP的影响。

在数学上，线性叠加可看成稳态反应由瞬态反应与刺激序列卷积得到。基于上述模型，Özdamar等提出了连续循环平均去卷积技术(continuous loop averaging deconvolution, CLAD)[3-5]。该技术改变固定SOA形式的刺激序列，引入小范围的抖动，避免了去卷积计算中奇异值问题。利用CLAD方法得到的40 Hz瞬态反应可根据叠加理论合成40 Hz的稳态反应。实验表明，该反应和实际记录的40 Hz稳态反应充分吻合，并由此推断稳态反应和瞬态反应有相同的神经起源[6]。同样基于线性叠加理论，Gutschalk等利用多个刺激率下稳态脑磁反应，重建瞬态反应[7]。Wang等在上述方法的基础上引入正则化技术解决了逆变换过程中的病态矩阵问题，提出多刺激率稳态平均去卷积技术(multi-rate steady-state averaging deconvolution, MSAD)[8]。MSAD把多组不同刺激率下的稳态反应拼接起来，将卷积运算转化为线性方程组的形式。因此，重建瞬态反应转化为线性方程组求逆的过程[9-11]。与CLAD技术一样，MSAD技术采用一系列频率相近的刺激序列，以减少听觉神经适应性所引起的非线性误差。

MSAD技术假设刺激率相近的稳态反应是近似一致的，也就是认为它们都是由一个确定的瞬态反应叠加而成，其对应的刺激率用各个稳态刺激率的算术平均表示。但是，目前尚不清楚不同刺激率导致的误差是否明显，是否存在偏离平均刺激率的稳态反应误差增大的情况。为此，笔者记录了20位成人的稳态反应数据，其中包括平均刺激率约为40 Hz的8个不同刺激率的稳态反应；并采用MSAD技术重建瞬态反应，以此合成稳态反应。通过对比合成稳态反应(synthetic ASSR, sASSR)与记录稳态反应(recorded ASSR, rASSR)之间的误差，探讨在这种情况下稳态反应的一致性和叠加原理的适用性。

1 材料和方法

1.1 原理

单次声音刺激诱发的瞬态AEP记为x(t)。离散化的刺激序列hi(t)用一组{1, 0}的二值序列表示，其中“1”表示刺激起始，相邻刺激之间补零组成一个刺激周期。如果刺激周期M小于瞬态反应时长N，会产生与刺激序列周期相等的周期性稳态反应yi(t)。这一过程可用如下卷积模型描述为

(1)

式中，⊗为循环卷积。

如果分别把瞬态反应和稳态反应写成向量形式，则式(1)可改写成矩阵的形式，有

yi=hix

(2)

式中，hi是一个M×N的循环矩阵。

矩阵的行向量由刺激序列的循环移位生成。MSAD技术通过刺激序列间SOA抖动引起刺激序列的刺激率不同，其诱发的瞬态反应假设不变。每个刺激率下的线性叠加模型均可以由式(2)来表示。假设有n组刺激序列，则会得到n个稳态反应，对应于n个线性方程。如果把记录的n个稳态反应拼接起来，得到向量y=[y1, y2,…,yn]T，则有

y=Hx

(3)

重建瞬态反应x本质上是矩阵的逆变换问题，即

(4)

由于矩阵H是由{0, 1}组成的二值稀疏矩阵，通常是病态，无法直接求逆。针对这个问题，MSAD方法引入了Tikhonov正则化[12]，截断奇异值分解[13]等技术估计其最佳近似解。

1.2 实验设计

受试者为20名健康成年人，包括7名女性，平均年龄22岁。本实验经附属南方医院伦理委员会批准，所有受试者均签署批准的知情同意书。实验设备采用澳大利亚Compumedics公司生产的NeuroScan SynAmps2系统。实验过程中要求受试者放松平卧，尽量保持不动。在使用磨砂膏去除局部角质层后，放置记录电极于前额正中发际处，参考电极于右耳耳垂，眉心电极接地，电极阻抗≤5 kΩ。采样频率20 kHz，放大增益10 000，滤波范围10～1 000 Hz。分别获取每位受试者在8组不同刺激率下稳态反应。采用单极性0.2 ms时长的click刺激声(82 dB SPL)，刺激率由小至大依次为27.2、31.3、34.7、36.8、39.1、41.7、48.1、52.1 Hz，平均刺激率为38.9 Hz。上述各刺激率随机次序给出，每组刺激给声约2 000次。

1.3 数据分析方法

以均值±标准差的形式表示V-Na峰峰值和V波潜伏期；运用配对样本t检验方法，分别验证这两项参数在记录稳态反应和合成稳态反应之间的差异是否具有统计意义；并进一步运用配对样本t检验方法，验证20个受试者在每个时刻点的记录稳态反应和合成稳态反应的波形之间是否存在统计差异。P<0.05时认为具有统计学差异。

以均方根(root mean square, RMS)意义下的相对误差作为量化评估合成稳态反应与记录稳态反应之间误差大小的指标，在数学上为残差RMS与记录稳态反应RMS的比值，表示为

(5)

式中，yr[k]是记录稳态反应，ys[k]为合成稳态反应，K表示一个稳态反应周期的长度。

2 结果

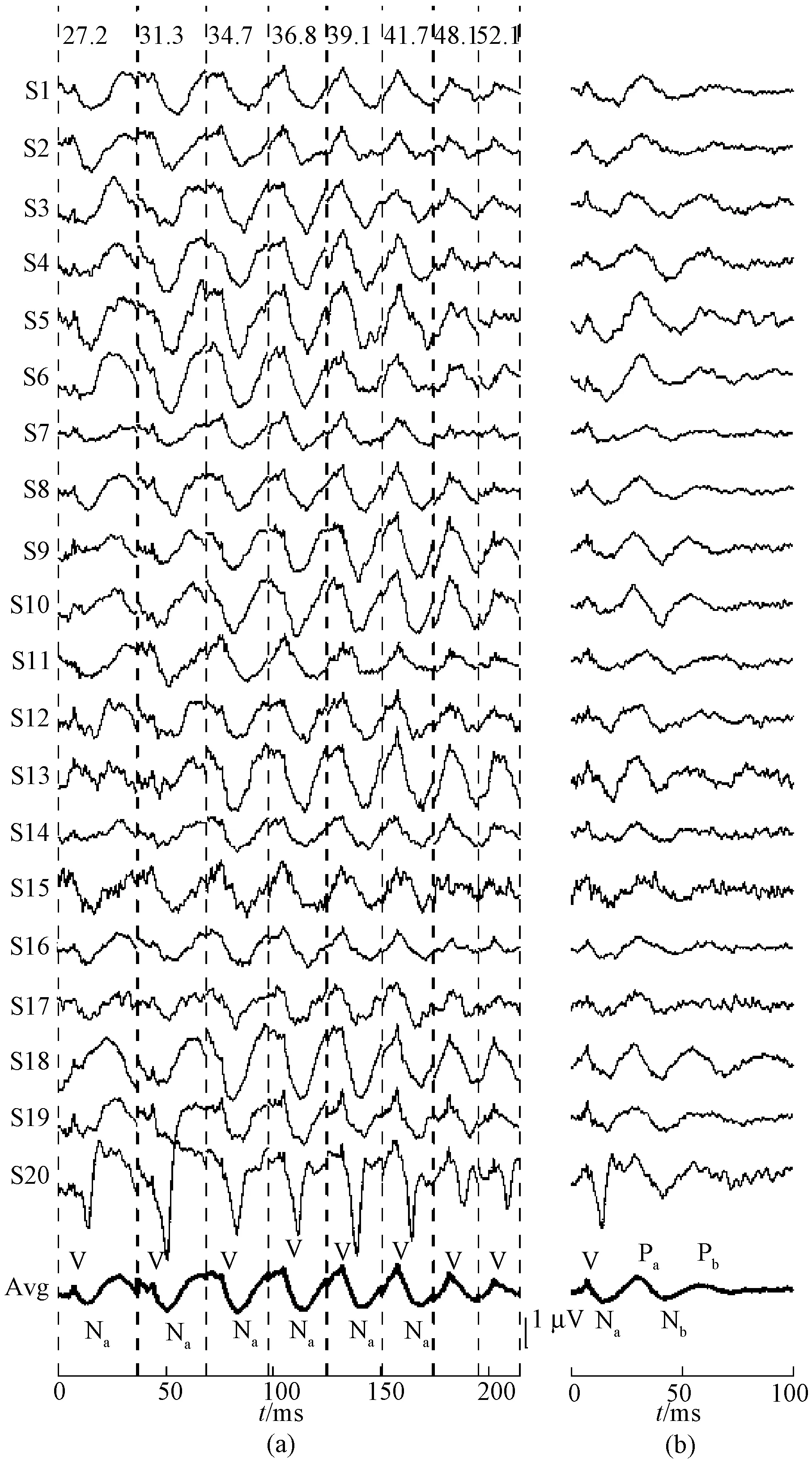
图1 MSAD方法重建瞬态反应(图上方的数字表示刺激序列频率(Hz))。(a)拼接的稳态反应；(b)重建的瞬态反应 Fig.1 Restore the transient AEP using MSAD method with stimulus rates (Hz) at the top of the figure. (a) Spliced ASSRs; (b) Transient AEP

分别获取每位受试者在8组不同刺激率下的一个周期的稳态反应，经过平均迭加的稳态反应按刺激率顺序头尾相接在一起，得到的拼接波形如图1(a)所示。图中以竖虚线分割了对应刺激率下的稳态反应。图1(a)共有21组稳态反应波形，其中20组细实线显示了单个受试者(分别以S1～S20标记)的稳态反应波形。通常个体AEP波形差异较大，最下面的一组以粗实线表示所有受试者的总体平均波形(以Avg标记)。从这些稳态反应中可以清楚辨认出所叠加的瞬态成分，如ABR的V波，而V波之后的波谷主要是中潜伏成分Na波。大部分的个体波形与总体平均波形类似，但S20有所不同，其Na波潜伏期明显小于总体平均值，在高刺激率下依然能被引出。采用MSAD方法对拼接稳态反应做去卷积运算，得到重建的瞬态反应，如图1(b)所示。无论是个体AEP还是总体平均AEP，V波，Na、Pa、Nb和Pb等主要成分均清晰可辨。其中V-Na峰峰值为(0.93 ± 0.36) μV。

基于线性叠加理论，稳态反应可以由瞬态反应与刺激序列卷积运算来合成。表1和表2分别从V-Na峰峰值和V波潜伏期来对比合成稳态反应和记录稳态反应。

稳态反应中的V-Na峰峰值如表1所示。鉴于高刺激率(48.1 和52.1 Hz)下刺激间隔较短导致Na波显示不完整的现象，取该刺激率下稳态反应最后时刻点的幅值代替。由表1可见，在39.1 Hz刺激率下，记录稳态反应的V-Na峰峰值最大，达到1.74 μV，36.8和41.7 Hz时则略小，分别为1.71和1.70 μV。合成稳态反应也有类似现象。无论是均值还是标准差，记录稳态反应和合成稳态反应都非常接近，其均值的比值接近于1。运用配对样本t检验方法(α=0.05)，结果显示记录稳态反应和合成稳态反应的V-Na峰峰值之间不存在统计差异。

表1 稳态反应的V-Na峰峰值(n=20；均值±标准差)Tab.1 The peak-peak amplitude of V-Na of ASSR (n=20; mean ± SD)

注：*标注了刺激率为48.1和52.1 Hz时， Na波峰值取稳态反应最后时刻点的幅值。

Note:*The amplitude at the end of ASSR is regarded as the peak amplitude of Naat 48.1 and 52.1 Hz rate.

稳态反应中的V波潜伏期如表2所示。无论是记录稳态反应还是合成稳态反应，随着刺激率增加，V波潜伏期变大，且两者的均值和标准差都非常接近，其均值比值接近于1。配对样本t检验(α=0.05)显示记录稳态反应和合成稳态反应的V波潜伏期不存在统计学差异。

合成稳态反应与记录稳态反应的误差情况并不完全一致，如图2所示。

表2 稳态反应的V波潜伏期(n=20; 均值±标准差)Tab.2 The latency of wave V of ASSR (n=20; mean±SD)

图2 记录稳态反应与合成稳态反应之间的误差(图上方的数字表示刺激率(Hz))Fig.2 Difference between recorded ASSRs and synthetic ASSRs with stimulus rates (Hz) at the top of the figure

在图2中，以竖虚线分割了对应刺激率下的误差片段。其中，上半部分每个曲线(分别以S1～S20标记)代表了单个受试者稳态反应的误差，对20个受试者在每个时间点做配对t检验(α=0.05)，结果如图2中Avg曲线所示。实直线为零值基线，实曲线为所有受试者稳态反应误差的总体平均值，沿基线上下对称的两条虚曲线表示为0.95置信区间。误差平均值位于置信区间内表示满足零假设，这意味着合成稳态反应与记录稳态反应之间不存在统计差异。基线上的实心点表示该时刻点的误差已经超过置信区间，这意味着，合成稳态反应与记录稳态反应在这些时刻点上是存在统计差异。由Avg曲线可见，在39.1和36.8 Hz的刺激率下，所有时刻点上的误差均位于置信区间内，即不存在统计差异。而其他刺激率下均sASSR与rASSR存在不同程度的差异，其中差异点最多的是41.7 Hz，达到13.75%。对误差进行分析，如图3所示。

图3 误差分析。(a)稳态反应残差的RMS，(b)记录稳态反应的RMS，(c)相对误差Fig.3 Error analysis. (a) RMS of residual errors; (b) RMS of recording ASSRs; (c) Relative error between ASSRs

图3(a)为合成稳态反应与记录稳态反应之间残差的RMS值，以方形实心点表示对应刺激率下残差RMS均值，条状线为标准差，图中显示了残差的RMS不随刺激率单调变化。图3(b) 为记录稳态反应的RMS值，结果表明在34.7、36.8、39.1、41.7 Hz这4个刺激率下，记录稳态反应RMS值最大。图3(c) 为相对误差，曲线显示了在8个刺激率中，52.1 Hz刺激率下相对误差最大，接近28%，而其他7个刺激率下的相对误差均在10%左右，其中36.8 Hz刺激率下的相对误差最小，为7.95%。

3 讨论

MSAD是一种基于线性叠加理论重建高刺激率瞬态反应的新技术。该方法假定相近刺激率诱发的瞬态反应是一致的，在数学上将瞬态反应与多组刺激序列的卷积运算转化为线性方程组的形式，通过求逆运算实现对瞬态反应的重建。本研究采用此技术重建了20个受试者的高刺激率下瞬态反应，对照分析了合成稳态反应与记录稳态反应之间的异同。并进一步研究了MSAD技术恢复瞬态反应过程中，刺激率的变化对重建质量的影响。

有研究表明，在常规瞬态反应中，刺激率的提高会导致Pb波的衰减[14-15]。而Özdamar研究团队采用CLAD去卷积技术重建瞬态反应，发现在不同的刺激率下，均能稳定引出瞬态反应中的Pb波，其中39.1 Hz的刺激率下，Pb波成分得到了强化[16-17]。本研究结果显示，无论是个体ASSR还是总体平均ASSR，瞬态反应的V波、Na、Pa、Nb和Pb等主要成分均清晰可辨，验证了MSAD去卷积技术的有效性。

前期研究结果发现， 40 Hz稳态反应的幅度是最大的[18]。有理论认为，40 Hz稳态反应不仅仅是瞬态反应的线性叠加，其中特征波成分的共振现象进一步强化了稳态反应[16]。表1的结果显示了在39.1 Hz刺激率下，稳态反应中的V-Na峰峰值最大。图3(b) 显示了记录稳态反应RMS值随刺激率变化的规律，其中在34.7～41.7 Hz区间内的RMS明显高于其他刺激率，这种现象与文献报道的研究结果是一致的。

表1和表2分别对比分析了合成稳态反应与记录稳态反应的V-Na峰峰值和V波潜伏期。结果显示，无论是均值还是标准差，两者都非常接近。配对样本t检验的结果显示，无论是V-Na峰峰值还是V波潜伏期，均不存在统计差异。合成稳态反应与记录稳态反应的特征波成分在幅值和潜伏期充分的吻合，有力地支持了稳态反应的线性叠加理论。

对于每个时刻点，配对t检验的结果显示，在平均刺激率为38.9 Hz的8组稳态反应中，只有36.8和39.1 Hz时的稳态反应，所有时刻点的残差均值均在0.95置信区间内，即合成稳态反应与记录稳态反应之间不存在统计差异。图3(c)中的相对误差也表明，36.8 Hz刺激率下的相对误差最小，而51.2 Hz的相对误差最大。上述结果支持MSAD技术基本假设，即刺激率相近的瞬态反应波形是近似一致的，合成的稳态反应也与记录稳态反应最吻合。同时，这也提示了采用MSAD去卷积技术重建瞬态反应，应该选择刺激率相近的序列以减少非线性误差。

4 结论

本研究采用MSAD技术，重建了20个受试者的瞬态反应，无论在个体AEP还是在总体平均AEP波形中，V波、Na、Pa、Nb和Pb等主要成分均清晰可辨。进一步，基于线性叠加理论合成了稳态反应，与记录稳态反应对比，发现两者的V-Na峰峰值和V波潜伏期基本一致。采用配对t检验分析每个时刻点，结果显示了在36.8和39.1 Hz刺激率下，合成稳态反应与记录稳态反应之间不存在统计差异。分析两者相对误差可见，36.8 Hz刺激率下的相对误差最小，而51.2 Hz的相对误差最大。总之，实验结果表明，合成稳态反应与记录稳态反应是吻合的，支持线性叠加理论，稳态反应和瞬态反应可能源于同一神经机制。综上所述，刺激率在适当范围内的变化对诱发反应的影响较小，采用MSAD技术重建高刺激率瞬态反应是合理可行的。

[1] Regan D. Comparison of transient and steady-state methods [J]. Ann NY Acad Sci, 1982, 388:45-71.

[2] Galambos R, Makeig S, et al. A 40-Hz auditory potential recorded from the human scalp [J]. Psychology, 1981, 78(4): 2643-2647.

[3] Delgado RE, Özdamar O. Deconvolution of auditory evoked potentials obtained at high stimulus rates. [J]. The Journal of the Acoustical Society of America, 2004, 115:1242-1251.

[4] Özdamar O, Bohórquez J. Signal to noise ratio and frequency analysis of continuous loop averaging deconvolution (CLAD) of overlapping evoked potentials [J]. The Journal of the Acoustical Society of America, 2006, 119:429-438.

[5] Özdamar O, Delgado RE, Yavuz E, et al. Deconvolution of auditory evoked potentials obtained at high stimulus rates[C] // First International IEEE EMBS Conference on Neural Engineering. Capri: IEEE, 2003: 285-288.

[6] Mcneer RR, Bohórquez J, Özdamar O. Influence of auditory of auditory stimulation rates on evoked potentials during general anesthesia: relation between the transient auditory auditory middle-latency response and the 40-Hz auditory steady state response [J]. Anesthesiology, 2009, 110(5): 1024-1035.

[7] Gutschalk A, Mase R, Roth R, et al. Deconvolution of 40 Hz steady-state fields reveals two overlapping source activities of the human auditory cortex[J]. Clinical Neurophysiology, 1999, 110(5): 856-868.

[8] Wang Tao, Zhan Changan, Yan Gang, et al. A preliminary investigation of the deconvolution of auditory evoked potentials using a session jittering paradigm [J]. Journal of Neural Engineering, 2013, 10(2): 026023.

[9] 朱程，王涛，黄江华,等. 40 Hz瞬态听觉诱发电位中潜伏期成分的引出分析[J]. 中国生物医学工程学报, 2013.32(5):539-545.

[10] 冯洁婷, 颜刚, 王涛,等. Tikhonov正则化参数选择对高速率刺激听觉诱发电位重建的影响[J]. 航天医学与医学工程, 2012. 25(1): 54-60.

[11] 冯洁婷, 颜刚, 鲜星宇,等. L-曲线估计正则化参数对高速率刺激听觉诱发电位重建的影响[J]. 中国生物医学工程学报, 2012, 31(2): 237-246.

[12] Tikhonov AN, Arsenin VY. Solutions of Ill-Posed Problems [M]. New York: Wiley, 1977.

[13] Hansen PC, Voldgade O. The truncated SVD as a method for regularization BIT Numer[J]. Math, 1987, 27:1487-1503.

[14] Tucker DA, Dietrich S，Harris S. Effects of stimulus rate and gender on the Auditory evoked Middle Latency Response [J]. Journal of the American Academy of Auditory, 2002, 13:146-155.

[15] Özdamar O, Krausa N. Auditory middle-latency response in humans [J]. Audiology, 1983, 22:34-49.

[16] Bohórquez J, Özdamar O. Generation of the 40-Hz auditory steady-state response (ASSR) explained using convolution [J]. Clinical Neurophysiology, 2008,119: 2598-2607.

[17] Özdamar O, Bohórquez J. Suppression of the Pb(P1)component of the auditory middle latency response with contralateral msaking[J]. Clinical Neurophysiology, 2008,119: 1870-1880.

[18] Hari R, Hamalainen M, Joutsiniemi SL. Neuromagnetic steady-state responses to auditory stimuli [J]. J Acoustic Soc Am, 1989, 86: 1033-1039.

An Assessment of Linear Superposition Conditions for 40 Hz Auditory Steady-State Responses

Lin Lin Tan Xiaodan Wang Tao*

(SchoolofBiomedicalEngineering,SouthernMedicalUniversity,Guangzhou510515,China)

Multi-rate steady-state averaging deconvolution (MSAD) is a newly developed method to restore the transient auditory evoked-potential (AEP) from the auditory steady-state responses (ASSRs) based on superposition hypothesis. This method requires that the variation of stimulus rates impose no substance influence on the response so that the model is applicable and viable. In this study, we recorded eight ASSRs from 20 subjects of 40-Hz average rate (from 27.2 Hz to 57.1 Hz), from which the transient AEP can be derived by the MSAD method. The AEP was then used to synthesize the ASSRs at the same recording rates. By comparing them with the recorded ASSRs, we examined the differences on the featured waves and the ASSR morphology. Results showed the peak-peak amplitudes of V-Na and the latencies of wave-Vs were close, and no statistic difference between recorded ASSR and synthetic ASSR at 36.8 and 39.1 Hz, whereas the minimum relative error of 7.95% was achieved at 36.8 Hz ASSR. It can be concluded that the stimulus rate has little effect on the responses within these range, which justifies the applicability of the MSAD method.

auditory steady state response; multi-rate steady-state averaging deconvolution; linear superposition theory

10.3969/j.issn.0258-8021. 2016. 03.004

2015-08-30， 录用日期:2016-03-16

国家自然科学基金(61172033，61271154)

R318

A

0258-8021(2016) 03-0278-06

*通信作者(Corresponding author)， E-mail: taowang@smu.edu.cn