无机脆性玻璃光窗抗鸟撞分析

杜兴刚，彭志军，秦利军，叶彬

（中航工业洪都，江西南昌330024）

无机脆性玻璃光窗抗鸟撞分析

杜兴刚，彭志军，秦利军，叶彬

（中航工业洪都，江西南昌330024）

通过选取鸟体模型、载荷接触面形式及解耦载荷数学模型，结合刚性靶理论，分别采用解耦解法、耦合解法对某无机脆性玻璃光窗进行了抗鸟撞分析，并对两种算法下的计算结果进行了比较。研究结果表明，无机脆性材料可以采用最大主应力破坏准则作为玻璃的失效准则；对于无机脆性玻璃，可用解耦解法进行分析，计算得到的临界速度与耦合解法得到的十分接近；采用解耦算法进行无机脆性玻璃材料鸟撞分析时，载荷接触面形状采用圆形面优于椭圆面。

无机脆性玻璃；光窗；鸟撞；失效准则；接触面形状

随着新一代飞机低空高速飞行性能的提高，以及低空高速飞行任务的增加，使得飞机撞鸟的概率也随之增加。目前，对飞机机头罩、风挡、机尾翼前缘、发动机叶片[1-8]等易遭受鸟撞的结构，开展了大量的试验和分析研究，积累了丰富的试验和分析数据，但随着航空技术的发展，特别是具有侦察或火控功能的红外光电系统出现后，对特定波段有高透光率的无机脆性材料[9-11]制成的光窗应运而生，光窗一般位于前机身机腹下方，突出飞机外形，极易遭受飞鸟的撞击。

蓝宝石是一种对特定波段有高透光率的无机脆性材料，国外由于具有生产大尺寸蓝宝石的技术，而蓝宝石又具有优异的力学性能，所以在光窗上得到了广泛的应用，试验、分析技术比较成熟。但国内目前还不具备生产大尺寸蓝宝石的技术，光窗主要选用性能相对较差的ZnS等材质的无机脆性玻璃，并且其价格昂贵，因此，很少开展抗鸟撞分析和试验。为了获得某光窗抵抗鸟撞的能力，掌握无机脆性玻璃的鸟撞分析方法，本文采用解耦和耦合两种解法对某光窗进行了抗鸟撞分析，结合试验测试结果，确定了其破坏准则，经过对不同鸟撞接触面的比较分析，确定了解耦分析时鸟撞接触面加载形状。

1 光窗结构简介

本文分析的无机脆性玻璃光窗采用的是多面体形状，如图1所示，前缘两侧为相同厚度的无机脆性玻璃，骨架为铝合金材料。

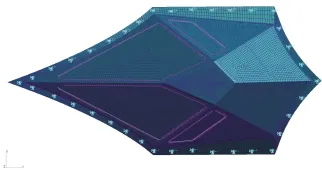
图1 光窗模型

2 鸟撞分析

鸟撞数值模拟方法是从20世纪80年代初开始的，它可分为解耦解法和耦合解法[12-13]两种。解耦解法采用方形或三角形等形式的载荷模拟鸟撞载荷，然后将此载荷作为已知条件施加到撞击面上，单独求解结构的动力响应。耦合解法建立鸟体和结构的有限元模型，通过接触部位的协调条件进行求解。

2.1 耦合解法

耦合解法一般借助商用有限元分析软件进行，目前常用的有MSC/Dytran、LS-DYNA、PAM-CRASH等。本文采用LS-DYNA软件分析无机脆性玻璃光窗抗鸟撞性能，前后处理采用LS-PrePost。

由于不同的鸟体形状对计算结果的影响不是很大[14-15]，鸟体采用质量为1.8kg，长径比为2:1的圆柱体形状和可压缩泡沫材料模拟；无机脆性玻璃及金属骨架采用4节点SHELL单元模拟。无机脆性玻璃与金属骨架共节点连接，模型中在金属骨架周边节点施加简支约束，鸟体与无机脆性玻璃的接触方式为点面接触。

2.2 解耦解法

解耦解法认为，鸟撞结构过程中关心的是结构的响应和损伤情况，鸟体本身并不是关心的对象，通过试验得出鸟撞载荷的变化规律，然后将此载荷作为已知条件施加到结构上，单独求解结构的动力响应，因此求解鸟撞载荷是关键。

由于本文研究的无机脆性玻璃弹性模量是有机玻璃的二十几倍，与铝合金材料的弹性模量相当，此类光窗面积相对于1.8Kg的鸟体模型较小，光窗结构本身的变形对撞击的结果影响可忽略，因此，计算鸟撞载荷时，采用刚性靶假设而没有采用柔性靶假设[13]。

刚性靶理论将光窗(无机脆性玻璃)假设为刚体，将鸟体假设成流体，认为整个撞击过程中撞击在光窗上的流体速度和质量相同。其撞击模型如图2所示，鸟撞击载荷是从零逐渐上升至峰值，然后，从峰值下降为零，载荷峰值上升时间一般占整个撞击周期的五分之一，因此给出三角波载荷计算公式如下：

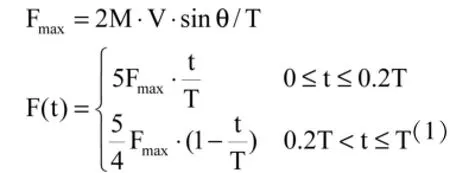
其中：

式中：M—飞鸟质量（Kg）；

V—飞鸟速度（m/s）；

D—鸟体直径（mm）；

L—鸟体长度（mm）；

Leff—鸟体有效长度（mm）；

θ—飞鸟运动轨迹与接触表面的夹角。

图2 刚性靶模型

由于鸟体模型为圆柱，载荷加载面通常有圆形和椭圆形两种，圆面面积为圆柱鸟体的截面积，椭圆面积为圆柱鸟体沿撞击方向在撞击面上的投影。鸟体高速撞击时呈现流体特性，因此模型中采用压力加载，并且假定接触面压力均匀分布，压力面积如图3所示。

3 材料破坏准则

脆性材料在动态载荷下比静态载荷下有更高的承载能力，这种现象常被称为材料动态破坏强度的应变率效应。同时也有各种瞬时破坏理论，如最大应力准则、最大应变准则、最大应变能准则[16]以及均强度破坏准则[17]等。但由于具有红外透波性能的材料极其昂贵，特别是面积较大的块体材料，通过试验测得的相关动态力学性能参数较少，由此制约了最大应变准则和最大应变能准则的应用。

图3 撞击位置及接触面积示意

对某无机脆性玻璃光窗进行了鸟撞试验，玻璃粉碎性破坏，测得的应变如图4所示。

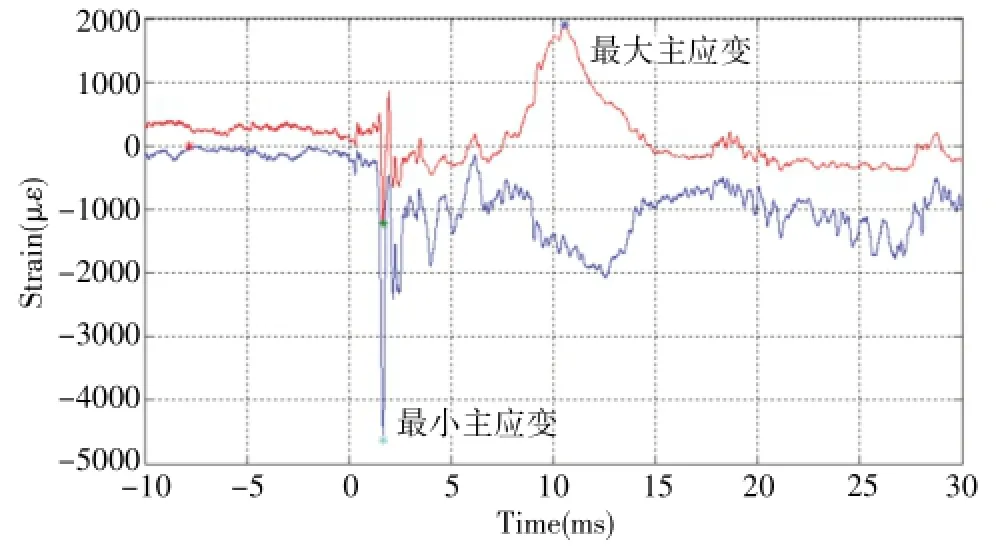
图4 撞击点主应变

由图4可知，应变变化趋势与三角波载荷假设类似，撞击点处应变值较大，在10.5ms达到最大主应变约1900με，ZnS玻璃的弹性模量为74.5GPa，泊松比0.28，强度极限为50MPa，最大破坏应变为671με，使用最大应变作为玻璃的破坏判据与已知的材料性能明显不符，结合该试验结果，经过耦合和解耦仿真对比分析得出，采用最大主应力破坏准则作为玻璃的失效准则较为合理。

4 仿真结果及分析

4.1 耦合解法

耦合解法经LS-DYNA软件迭代计算，计算中采用拉格朗日解法，得到玻璃抗侧面撞击的临界速度为210km/h，侧面撞击过程中玻璃的最大主应力-时间变化曲线如图5所示。

4.2 解耦解法

先给定一个鸟体速度，采用式（1）计算出鸟撞载荷后，再采用MSC.Patran/Nastran进行分析，不断进行迭代计算鸟撞临界速度，有限元加载时采用圆形面和椭圆面两种形式。

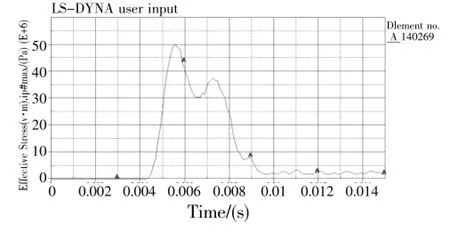
图5 玻璃最大主应力

圆形接触面撞击时玻璃的最大主应力如图6所示，玻璃抵抗侧面撞击的临界速度为200km/h。

椭圆接触面撞击时玻璃的最大主应力如图7所示，玻璃抵抗侧面撞击的临界速度为265km/h。

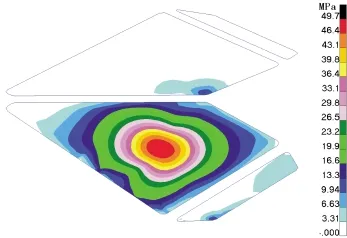
图6 圆形接触面侧面撞击玻璃的最大主应力

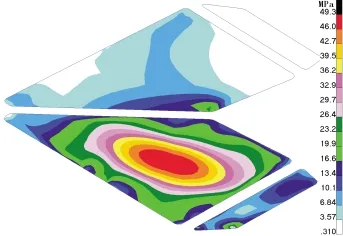
图7 椭圆接触面侧面撞击玻璃的最大主应力

两种不同接触面下的解耦解法与耦合解法计算得到的临界速度见表1所示，耦合解法得出的临界速度与采用圆形接触面加载得到的临界速度更加接近，与采用投影椭圆面加载得到的临界速度差距较大，采用圆形接触面更加合理，这是因为沿着玻璃表面方向，鸟体对玻璃的撞击很弱，如果按投影椭圆面加载，垂直玻璃表面的载荷大小不变，但面积增大很多，所以计算得出的临界速度偏大。

通过前面的分析可知，采用最大主应力破坏准则作为失效准则时解耦和耦合两种算法得到的临界速度基本相同，因此，采用最大主应力破坏准则是合适的。

表1 两种算法及不同接触面鸟撞临界速度比较

5 结论

通过前文的分析可得出以下结论:

1)对于无机脆性玻璃，可用解耦解法进行分析，并且计算得到的临界速度和耦合解法得到的十分接近；

2)对于无机脆性玻璃材料的鸟撞分析，可以采用最大主应力破坏准则作为玻璃的失效准则；

3)采用解耦算法进行无机脆性玻璃材料鸟撞分析时，接触面积形状采用圆形面积优于椭圆面积。

[1]谢宗蕻，卞文杰，等.峰窝夹芯结构雷达罩鸟撞有限元分析与模拟.爆炸与冲击，1999，19（3）：235-242.

[2]万小朋，龚伦，赵美英，等.基于ANSYS/L S—DYNA的飞机机翼前缘抗鸟撞分析.西北工业大学学报，2007，25(2):285-289.

[3]赵楠，薛璞.机翼前缘结构抗鸟撞分析研究.科学技术与工程，2010，10(8):1911-1914.

[4]张永康，李玉龙.不同构型梁-缘结构抗鸟撞性能分析.机械科学与技术（西安），2007，26(12): 1595-1599.

[5]张志林，姚卫星.飞机风挡鸟撞动响应分析方法研究.航空学报，2004，25(6):577-580.

[6]臧曙光，武存浩，汪如洋,等.飞机前风挡鸟撞动响应分析.航空材料学报，2000，20(4):41-45.

[7]彭迎风，滕春明.飞机风挡鸟撞动响应分析方法研究.南昌航空工业学院学报(自然科学版)，2003，17（4）：27-31.

[8]白金泽，孙秦.飞机风挡结构抗鸟撞一体化设计技术研究.力学与实践，2005，27(1):14-18.

[9]许军锋，坚增运，常芳娥，等.红外透波材料的发展现状与展望.中国材料科技与设备(双月刊)，2006,5:28-32.

[10]聂辉，陆炳哲.蓝宝石及其在军用光电设备上的应用.舰船电子工程，2005，146（2）：131-133.

[11]张兴德，刘琳，李荣刚.机载光电设备红外窗口技术.红外与激光工程，2008,39（4）：601-606.

[12]王富生，岳珠峰，冯震宙，等.鸟撞飞机风挡动态响应数值模拟方法研究现状.飞机设计，2008，28 (5):39-46.

[13]张志林，张啟桥，李铭兴.飞机圆弧风挡鸟撞动响应分析.航空学报,1992,13(9):538-542.

[14]刘军，李玉龙，刘元镛.基于SPH方法的叶片鸟撞数值模拟研究.振动与冲击，2008，27（9）：90-93.

[15]朱书华，童明波.鸟体形状对飞机风挡鸟撞动响应的影响.南京航空航天大学学报，2008，40（4）：551-555.

[16]严成，欧卓成，段卓平，等.脆性材料动态强度应变率效应.爆炸与冲击，2011，31（4）：423-427.

[17]金宗哲，包亦望，脆性材料的均强度破坏准则.试验力学，1992，7（1）：94-99.

>>>作者简介

杜兴刚，男，1984年出生，2008年毕业于西北工业大学，工程师，现从事飞机强度设计工作。

Bird Impact-Resistant Analysis on Inorganic Brittle Glass Window

Du Xinggang,Peng Zhijun,Qin Lijun,Ye Bin
(AVIC Hongdu Aviation Industry Group,Nanchang,Jiangxi,330024)

By selecting the bird model,the form load contact surface and decoupled load mathematical model and based on the theory of rigid target,this paper carries out the bird impact-resistant analysis on a certain type of inorganic brittle glass window by the means of decoupling and coupling algorithm respectively,and carries out the comparison on the computing results of the two algorithms.The study result shows that(1)for inorganic brittle material,the max.stress rupture rule can be used as the failure criterion of glass;(2)decoupling algorithm can be used for analyzing inorganic brittle glass,and the decoupled critical speed is close to the coupled one;(3)when the decoupling algorithm is applied for the analysis of bird impact on inorganic brittle glass,the round load contact surface is better than the elliptical one.

inorganic brittle glass;optical window;bird impact;failure criterion;Shape of contact surface

2015-03-12)