方格巧数 见微知著——中国大陆、中国台湾、美国纽约州教材方格点数策略比较

□孙惠惠

方格巧数 见微知著
——中国大陆、中国台湾、美国纽约州教材方格点数策略比较

□孙惠惠

不同教材能帮助我们了解各地不同的教学特色，形成更具有包容性和吸引力的数学内容。通过对中国大陆、中国台湾、美国纽约州三地教材中方格点数策略的比较研究，从方法渗透、估算强化、表征建构等方面探讨了通过关注知识的结构性特点，形成有包容力的认知结构；通过关注经验的渐进性积累，形成有发展性的能力素养等问题与解决之法。

方格点数 教学策略 比较研究

《义务教育数学课程标准（2011年版）》对平行四边形的面积探索给出了非常具体的过程要求：“利用方格纸或割补等方法，探索并掌握平行四边形的面积公式。”方格纸从无到有，直至正式列入课程标准，这不得不让我们深思方格点数背后的现实价值所在。近期，有幸阅读了美国和中国台湾的数学教材，对学生在平行四边形面积探索中所需要的方格点数能力有了进一步的认识，对如何形成包容性、开放性的课堂教学也有了更进一步的思考。

一、方格点数教学策略实施的共性比较

方格点数是学生在图形面积学习过程中一种不可或缺的探索方法，也是一种难度较低，容易为学生所掌握的探索技能。虽然点数的方法比较麻烦，但最本源的方法往往是最有教育价值的方法。纵观三地教材，三地在方格点数策略实施中有很多共同点。

第一，在教材编排上，三地都在平行四边形面积公式推导前安排了方格点数的教学内容作为铺垫，但实施教学的课时、程度、侧重各有不同。

第二，在素材选择上，三地都不约而同地选择了面积是1平方厘米的方格图，识图便捷，累加简单。

第三，在方法选择上，三地都是充分运用单位面积累加，渗透面积的本质内涵。

第四，在教学实施过程中，教师鼓励学生通过数方格直观得出平行四边形的面积，为面积公式的探究孕伏经验基础；指导学生直接在方格纸上进行图形割补，直观呈现割补结果，降低探究难度；引导学生通过对方格纸中平行四边形和长方形的对比，发现平行四边形的底和高与长方形的长和宽之间的对应关系。

二、方格点数教学策略实施的差异比较

（一）中国大陆：注重点数方法的渗透和半格累加的教学

中国大陆现行的六套教材中，各套教材都在平行四边形面积教学之前对方格点数法进行了铺垫，不同程度地让学生接触过方格纸和点数方法，其中北师版和苏教版分别安排2课时和1课时的时间专门教学方格点数知识；西师版和青岛版利用对称、平移、旋转的教学让学生接触了方格纸。人教版则在平行四边形面积教学之后，单独安排了利用方格点数法求不规则图形面积的内容。教学中，主要渗透“单位面积个数累加就等于面积之和”的点数基本方法，如4个1平方厘米的小正方形所拼成的图形，它的面积是4平方厘米（见图1）。

图1

素材选择上，中国大陆的教材中大多将素材的选择限制在正好半格，引导学生掌握两个半格可以拼成一个整格的累加方法。对于不满半格的图形，教材中通常告知学生“不满一格”可以近似的看成一格，不满半格可以近似看成半格，初步渗透估算的思想（见图2）。

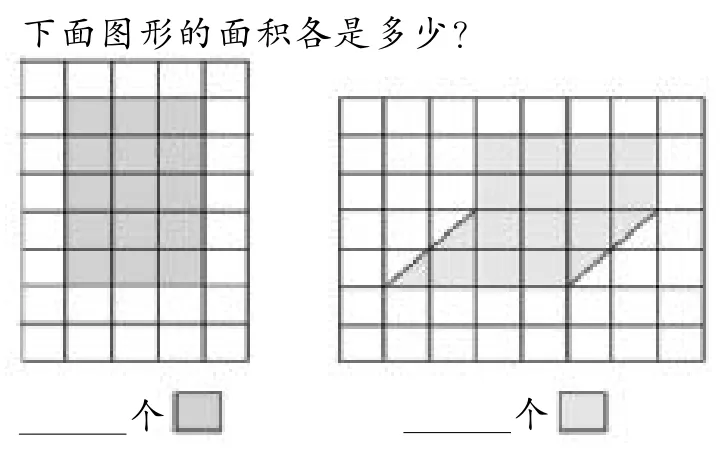
图2

（二）中国台湾：注重半格的基本表征和多元化应用

在中国台湾版的教材中，侧重半格的基本表征和半格表征的多元化应用。在教材中，你能够充分感受到对学生思维关注的细腻程度。教材不仅给出半格的概念，更给出了半格表征的两种方式（见图3）。

图3

第一种表征方式是沿对角线分割成两个相等的三角形，每个三角形的大小正好是半格；第二种表征方式是沿着对边的中点分割成两个相等的长方形，每个长方形的大小也正好是半格。

为了增强学生对于半格表征的运用，教材继续跟进利用半格表征方法表示更大面积的图形练习（见图4）。利用半格的不同表征，学生可以创造出各种个性化的表示方法，如1.5平方公分的表示方法就有很多种，有些学生甚至在半格的基础上继续拓展，创造出两个四分之一格可以表示半格的作品。在这个过程中，学生熟练运用方格点数技法的能力得以提升，解决非整数面积问题的能力也得到了迅速发展。

图4

统览中国两地的教材，我们可以发现，从“随意数”到“有方法地数”到最后“结构化地数”，这种最简单的也是最笨的方格点数法，正在不知不觉中提升着学生解决面积问题的实际能力。教材编写者在这些细微处的良苦用心，其实正来自于他们对面积本体知识的深度解读。

（三）美国纽约州：注重点数估算的强化和方法的系统化

美国在方格点数方法的教学中，侧重让学生理解怎样的几个“不满一格”可以近似的看成一格。如教材中给出了拉米雷斯先生利用网格来解决玻璃面积大小的问题，并给出了不满一格的部分如何计算面积的具体方法（图5）。如④、⑤属能于一格多一点点，可看成近似一格；①、②、③、⑦属于怎样的两格可以看成近似的一格；⑥、⑧、⑨属于怎样的三格可以看成近似的一格。这样给出具体实例的分析，既能让学生在实际单数中有方法指引和具体指导，又能够让学生在面对不同图形的点数过程提高估算的精准度。

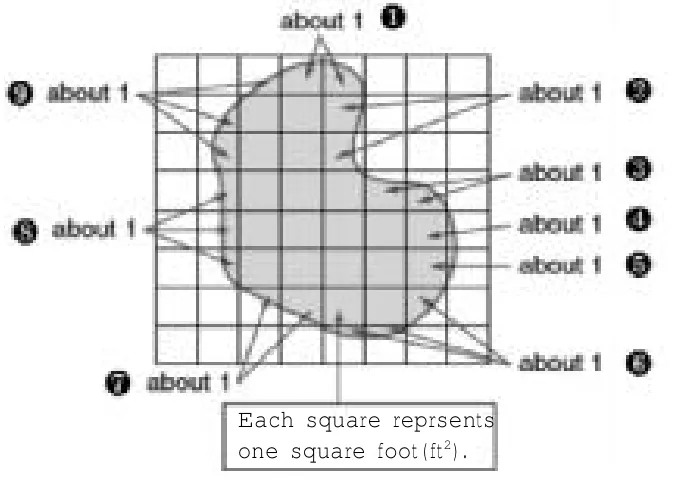
图5

同时，教材中还配以跟进型的练习，让学生在练习中，学会根据实际情境分析情况，恰当使用点数估算策略，熟练点数技能（见图6）。

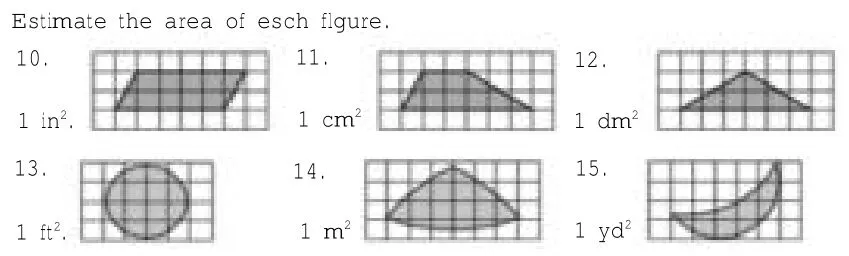
图6

三、教学启示与思考

方格点数不仅是面积度量中的一种重要方法，更是一种问题解决的方式。它有助于面积概念从具体到抽象的建构，有助于对度量过程的优化与抽象，更有助于学生对问题本质概念的理解与把握。

（一）理性认识累加，明确单位量累加的目的与意义

方块累加是学生的一种操作活动，具有很强的结构性。如12个面积1平方厘米的小正方形可以摆出如下图形（见图7），它们的面积都是12平方厘米，但这其中，只有②③④号是长方形。借助拼组活动，可以渗透“标准计量单位个数累加的和就是总面积”的面积守恒原理；同时在这个过程中引入一些数学词句，如“一行中有四个这样的标准单位”“每行的个数同样多”等等，用言语表征来强化图形表征的特点，进而加固经验，则会收到事半功倍的效果。而这些原始经验、操作经验的积累和数学规范语言的对接，会在以后的教学中产生重要的作用。

图7

（二）结合想象优化度量，掌握面积的逐步抽象过程

在空间度量的背景下进行方格点数，就能发现，方格点数的过程，其实就是“度量思想”逐步渗透，面积表象逐步抽象的过程（见图8）。

第一步：密铺感知。见图8-①，将12个小正方形完全密铺完，所以长方形的面积就是12个小正方形的面积之和。

图8

第二步：直观感知。见图8-②，在这个长方形中，第一行可以放4个小方格，可以放三行，那么这个长方形的面积就是4×3=12个。

第三步：估量感知。见图8-③，在这个长方形中，以这个小方块为标准单位进行测量，第一行可以放4个小方格，可以放三行，因此这个长方形的面积就是4×3=12个。在这一步中，学生已经有了“被测对象含有几个度量单位”的初步意识。

第四步：度量感知。见图8-④，没有标准单位可参考，只能根据度量来确定长和宽，从而确定沿着长或宽各可以摆放几个标准单位。

通过一次次的摆放和数，学生的数从“按个点数”到“按行点数”，从“按量（估计量）点数”到“按量计算”，充分感受到度量的逐步优化过程，感受到数学的抽象过程，以及抽象所带来的问题解决的便捷。

（三）丰富核心表征，凸显底和高的垂直关系

表征的丰富会带来表象的牢固建立与知识的深入理解，而核心表征的建立，在理解概念和算理中显得尤为重要。在长方形面积公式推导的教学中，尽管教师已经给出了尽量多元的表征，帮助不同层次的学生理解公式的形成过程，理解算式中各个数的含义。但在迁移到平行四边形面积计算公式的推导时，依然有学生会毫不犹豫地猜测是底和邻边相乘，还有部分学生在选择面积计算所需要的数字时，也会随意选择底和高，而不是选择互相垂直的一组底和高。这些行为不由得令我们思考，是不是我们所提供的面积表征出现了问题，才致使知识的迁移产生了误导。看来表征不仅需要多元，更需要突出底和高互相垂直的本质。

翻阅近10年的教学设计，我们可以明显地发现，长方形面积公式的抽象过程中，我们提供给学生的关于长和宽各包含多少个长度单位的例子，通常都是沿邻边摆放的（见图9-①），很少有沿非邻边摆放的例子（见图9-②③）。因此，在大量实例的强烈刺激下，学生无意中就对底（长边上计量单位的个数）、高（宽边上计量单位的个数）形成了错误的关联关系，引发后续公式推导的错误冲突。正是我们一直强调公式中是底×高，但在表征对应的一组底和高（互相垂直）时缺乏多元的表征，才使得学生疑惑，平行四边形面积中为什么必须选择和底边对应的高相乘？

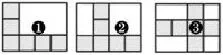
图9

至此我们已经可以掩卷深思：学生思维中的这些疑虑、这些误解、这些磕磕碰碰，都无一不在提醒着我们，该如何回到面积的本源展开教学，该如何借助操作活动、多元表征、理性解读来帮助学生形成更有包容力的认知结构。看来，表征不仅需要多元，更需要变式。基础知识的掌握程度直接决定着学生未来持续学习的能力！

[1]德里克·海洛克.数学教学ABC基本概念与核心理念[M].北京：教育科学出版社，2015.

[2]刘加霞.小学数学几何公式教学的教育价值分析——以“长方体的体积”为例[J].小学数学教学数学版，2012.

（浙江省宁波艺术实验学校 315040）

（注：本文作者系朱乐平数学名师工作站“一课研究”组成员）