利用数学史料 提升数学素养
——有效利用“数学史料”的教学策略
□邵汉民
利用数学史料 提升数学素养
——有效利用“数学史料”的教学策略
□邵汉民
编者按
著名数学史家M·克莱因提出“历史是教学的指南”。数学史料就是数学的历史,它自然就是数学教学的指南。教研员邵汉民老师自2008年开始,就致力于数学史料有效利用于数学课堂的实践研究,经历了学习、整理、教育学化与教学实践等几个阶段,积累了一些资料与教学经验。对此,本刊特邀请邵汉民老师及其团队组了一组专题,供大家参考。
数学史料是重要的数学背景性知识,数学史料为我们揭示数学知识的产生、形成与发展的过程。依据课程标准,结合教材内容,分析学生学情,把数学史料与数学知识点之间建立联系,创设数学史情境,设计教学流程,或把数学史料渗透于教学环节中,或融入于数学探究中,或作为课程开发的重要资源。让数学史料成为提升学生数学素养的不竭源泉。
数学史料 数学素养 教学策略
数学是人类文化的重要组成部分。数学的背景知识——数学史料,是体现数学文化气息的重要载体,从数学教材内容出发,收集、整理与数学知识相对应的数学史料,依据数学史料所提供的背景知识,创设具有浓厚的数学文化气息的问题情境,学生在数学学习过程中,不仅学到了数学知识与技能,也受到了数学的文化熏陶。基于这样的认识,近年来,笔者就如何有效利用数学史料,提升学生的数学素养展开了实践研究,总结了如下的教学策略。
一、渗透式教学
(一)直接引用
在数学史料中,有一些古人在长期的实践研究中积累的经典数学定义、法则与定理,虽然随着数学的发展,被埋入历史的尘埃,但是,如果能够进行合理的引用,却可以揭示数学的本质,加深对数学的理解。
例如教学“圆的认识”时,在学生已经理解了圆心、半径与直径的概念之后,教师谈话引入:
很早以前,人们就对圆进行了研究,发现了圆的规律。如春秋战国时期的一位大思想家墨子就对圆进行了研究,在他的一本著作《墨子·经上》中对圆有这样的描述:“圆,一中同长也。”(教师板书)谁能解释这句话的意思?
把墨子对圆的定义作为小结,很巧妙地把数学史有机地渗透于数学教学之中,相得益彰,使数学教学更有了一种文化的厚重感。这样的例子还有一些,如圆周率的近似值“周三径一”,描述圆的特征的“圆出于方”,试商的方法“折半商五”等等。
(二)创设情境
数学史料记录了许多数学概念在形成过程中的各种曲折与探索,教师可以根据学生的认识水平,创设情境,再现数学符号、法则与定律的形成过程,引导学生进行更加生动与深刻的数学思考。
例如,为加深学生对数学符号的社会约定性的初步认识,教师在介绍“+”的由来时,创设了如下的问题情境。
①教师出示:已知5⊥3=8,求8⊥5=( )
②学生独立完成后校对,并说出思路。
③提问:这题中的“⊥”相当于我们学过的哪一个运算符号?
④追问:如果全世界都用“⊥”代替原来的这个运算符号,你说可以吗?为什么?
⑤教师讲述“+”的由来。
数学中的运算符号是数学语言的重要组成部分,是一种世界通用的语言。但是在数学发展的某些阶段,它并不是统一的。通过上面的情境设置,可以让学生体会到数学符号由多元走向统一的过程。
从上例中也体现了我们的一个观点,渗透数学史知识不是简单地介绍它的历史,而是要让学生感受到数学发展的轨迹,体会数学的形成过程。
(三)习题改编
习题是数学教材的重要组成部分,为使习题更有人文气息,对于部分习题可以依据它们与相关数学史料的联系,进行适当的补充与改编,用数学史料润色平淡的数学题目。
如人教版数学二年级上第31页第12题(如下图)。

完成本题之后,可以把它改编为“洛书”。
完成第12题后,教师出示一个由1至9九个数组成的九宫格(下左图),请学生观察是不是也有第12题一样的规律?
拦河坝防渗沥青混凝土心墙顶高程2982.3m,沥青混凝土心墙通过开挖截渗槽坐落于强风化基岩上,基座下部岩石采用帷幕灌浆进行防渗处理。坝体沥青混凝土心墙与坝基防渗帷幕形成完整的防渗系统。
再出示“洛书”投影(下右图),问这像什么?它与我们刚才填的九宫格有什么联系?你喜欢看哪一幅图?
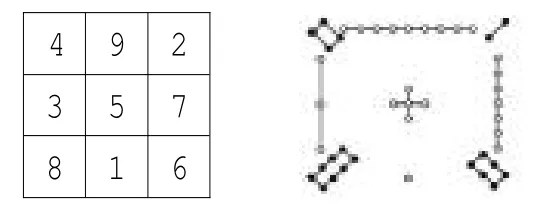
最后,教师讲述“洛书”的传说。
依据数学史料改编习题,可以丰富习题的文化内涵,使得习题变得更加生动,提高学生解题的兴趣。
(四)创编故事
我们这里的数学故事是从数学史料中引用或由数学史料加工而得到的故事,它既具有数学性,又具有趣味性与教育性。
如一上年级学生在学习了“10以内数的认识”之后,教师结合具体的图片,向学生讲述数字的由来。
教师首先依次出示如下图片,分别讲述在没有数字之前,古人是如何记录数量的。

再请学生评一评,与我们用数字记录相比,有什么不方便的地方?接着教师出示如下数字。

教师引导学生进行比较,我们现在用的1~9这几个数码与图中的记数方法有什么相似的地方,与它们相比又有什么优点?
(五)引用解题方法
解题方法既是解决问题的工具,也是解决问题的过程。在数学史料中,记录着一些现在已经不通用,但又可以拓展学生思维空间的解题方法,在合适的时机向学生介绍这样的解题方法,可以拓展学生的数学思路。
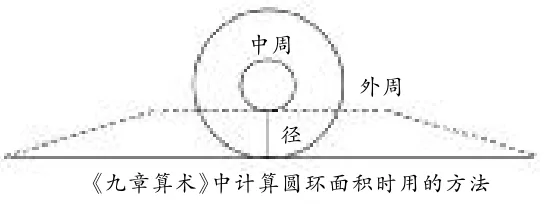
如在《九章算术》中,计算圆环面积时用的方法是“并中外周而半之,以径乘之为积步”。也就是用“圆环面积=(内圆周长+外圆周长)×圆环宽÷2”这种思路,其实质是把圆环“伸直”,使它成为等腰梯形,然后按梯形的面积计算公式的形式来进行计算,很有想象力。在六上年级学习了圆环的面积计算方法之后,教师可以介绍这一种方法,并请学生说明这样做的理由,再通过推理验证这样计算也是正确的。
这样的例子还有一些,如三角形面积计算公式推导中刘徽的“出入相补法”,多位数乘法中的“铺地锦”,测量时间中的“刻漏”等。
二、融入式教学
(一)融入问题解决之中
《义务教育数学课程标准(2011年版)》强调“让学生亲自经历将实际问题抽象成数学模型进行解释与应用的过程”。为此,教师在钻研教材时,要不断地追问:这些数学知识是如何形成的?它包含着哪些数学背景知识?它蕴含着怎样的数学思想?
《九章算术》对分数作了这样的定义:“(实)不满法者,以法命之”。刘徽对此注云:“凡实不满法者而有母子之名”。稍后问世的《孙子算经》讲得更加明白:“凡除之法,……实有余者,以法命之,以法为母,实余为子。”
从文献对分数产生的理解,分数是为了使除法得以普遍施行而引进的新数。与教材的引入相比,更能体现出数学在解决实际问题时进行的自我建构的轨迹(见下图)。

对要求学生掌握的数学概念、法则与公式,通过文献资料的查询,搞清在“成形”之前人们对它们的认识历程,并结合学生已有的生活经验与认识基础组织教学,让学生重走数学的探究之路。
(二)融入规律探究之中
小学数学的概念、定义、法则的产生与形成,大多经历了漫长的历程,在课堂上让学生真实地经历这样一个过程,是不可能也是没有必要的。在设计数学探究的过程时,我们通过阅读相关的数学史料,再结合学习现实,确定哪些过程适合于学生探究,哪些过程只要学生读史了解。
如圆周长的精确测量是一个千古难题,在对这个难题的破解中,人们发现了圆周率,并经历了实验时期、几何法时期、分析法时期、计算机时期这四个时期。当然,要在短短的40分钟内让小学六年级的学生亲身探究这样的一个过程,无论从时间与已有的知识基础来说都是做不到的。我们可以做的是,创设情境,在经历了用实验法只能得到圆周率的大致值的体验之后,介绍之后的关于圆周率的研究成果与方法。
数学探究的过程是曲折、漫长的,在数学发展的历史长河中,数学规律的发现一般经历猜想、实验、证明与公理化,就小学数学知识的获得,更多地依靠观察操作,再通过不完全归纳和合情推理来获得,也就是数学史料中记录着的数学产生与形成的初始阶段。
(三)融入探究策略之中
数学探究的过程,既是对学习材料的分析与加工的过程,更是创新数学思维的过程。在数学探究过程中,不同的探究视角,可以得到不同的数学思考过程。以史为鉴,可以寻找到全新的数学探究策略。
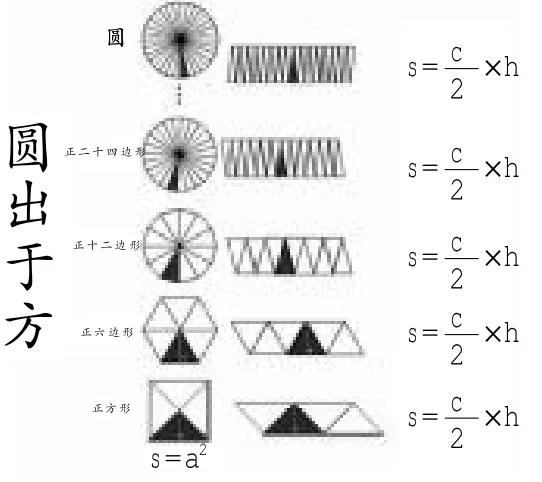
《九章算术》关于圆面积计算公式是:半周乘半径。这个公式是怎样推导的?《九章算术》中没有记载。笔者又查阅到,比《九章算术》更早的一本数学著作《周髀算经》中记载着“圆出于方”,就是说圆可以由正方形不断地切割得到,即圆可以看成是一个边数无限的“正多边形”。那么,是否可以从求多边形的公式中推导呢?依据这样的假设有了如下的推导思路。
综合可知,融入式教学是渗透式教学的深入,它关注的是从数学史料中寻找数学探究的因子,设计新知学习的新思路。
三、课程拓展式教学
(一)延伸教材中的数学素材
数学活动需要借助于一定的活动素材,活动素材可以是具体的实物,可以是现实的问题,还可以是抽象的数字或符号等。如人教版三年级上的“掷一掷”,五年级下的“哥德巴赫猜想”,六年级下的“七桥问题”等,都是借助于一定的活动素材开展的数学活动。进一步,可以适当延伸这些教材中的数学学习材料,可以进一步拓展数学学习的空间。
例如,把三年级上“掷一掷”中的活动材料——骰子从2颗增加到3颗,就可以提出新问题,形成新的数学活动了,题目如下。
同时任意掷3颗骰子,比较出现点数和为9与出现点数和为10的可能性的大小。
这是流传在欧洲的古老问题。由于被伟大的科学家伽利略解答过并作为推广“枚举法”的一个典型例子而更加有名。
教师可以在回顾教材中的“掷一掷”的问题之后,出示上面的题目,并介绍题目的作者与作者简介,然后让学生以四人小组为单位,在独立完成的基础上进行交流讨论,展示以下三次穷举。
(1)第一次穷举——分别穷举出点数和是9或10的组合
和是 9的点数组合是:(1,2,6)(1,3,5)(1,4,4)(2,2,5)(2,3,4)(3,3,3);和是10的点数组合是:(1,3,6)(1,4,5)(2,2,6)(2,3,5)(2,4,4)(3,3,4)。继而产生新的疑惑:组合的组数都是6组,到底哪种点数和获胜的可能性大呢?
(2)第二次穷举——穷举三类不同点数组合的实际操作的不同结果数
从实例(1,2,6)(1,4,4)(3,3,3),到通例(a,b,c)(a,a,b)(a,a,a),得出通例分别有6种、3种、1种结果。
(3)第三次穷举——穷举实际操作时可能的结果数
先通例与实例一一对应,再计算得出结果数。“点数和是9”在实际操作中可能的结果数:6×3+3×2 +1=25种;“点数和是10”在实际操作中可能的结果数:6×3+3×3=27种。
数学课程的拓展,首先要基于教材,在完成教材基本任务的基础上,依据数学史料,对相关的学习活动进行适当延伸,进一步提升学生的数学思维水平,也有利于数学活动经验的积累与基本数学思想的形成。
(二)充实教材中的数学内容
数学教材是最基础的、为后续学习所必须的数学内容的集合。显然,数学内容远不止教材中的内容。教师可以在充分钻研教材的基础上,对教材相关的内容进行充实,拓展学生的数学视野,丰富学生对数学的理解。
如四年级下介绍了“十进制计数法”。“十进制计数法”是“位值制计数法”中的一种特殊情况。所以,要真正理解“十进制计数法”需要从理解“位值制计数法”入手,体会“位值制计数法”的优越性,然后再将“其他位值制计数法”与“十进制计数法”进行比较,体会“十进制计数法”的优越性。
著名数学教育家弗赖登塔尔曾经说过:“没有一种数学的思想,以它被发现时的那个样子公开发表出来。一个问题被解决后,相应地发展为一种形式化技巧,结果把求解过程丢在一边,使得火热的发明变成了冰冷的美丽。”在数学知识形成之初,不论它的发现过程、抽象方式或表达形式,都带着地域特点与个性特征。随着人类的交往范围的不断扩大,这些数学知识也得以不断交流,不断完善,这应该就是“火热的发明”的过程吧。
(三)开发数学课程
数学教材并不是学生学习数学的唯一材料。因此,除了可以结合数学教材进行延伸与补充外,也可以依据掌握的数学史料进行数学拓展课程开发。从数学史料中寻找数学课程资源,可以极大地丰富数学教学资源。
数学拓展课程的开发,需要依据学情,遵循课标,并围绕某一个专题,形成一定的系列。如笔者以“常见的量”为专题,与一所学校的数学老师合作,开发了校本教材《度量衡的记忆》,课程分成两大部分,第一大部分是《“度量衡”回眸》,分成“度”“量”“衡”“时”“币”五个专题,介绍小学教材中这五类计量单位的发展历史。第二大部分是《“度量衡”的课例》,结合教学内容,在一至六年级每一个学期安排一个或两个课时的教学内容。这些内容由于更多的是从人文与历史的角度来编写,可读性强,教学有趣味,适合在全班进行教学。
另外,也可以开发数学社团活动资料,主要针对学有余力的学生,如笔者与教师团队一起,收集古今中外的并有一定故事背景的数学名题,编成《数学名人名题》系列丛书,既可以作为学生的课外阅读材料,也可以作为教师的社团活动教材。
总之,数学史料的有效利用,首先要对数学史料进行整理与充分理解;其次要对数学史料进行“教学化”,即与日常的数学教学相渗透或相融合;另外也可以把数学史料“课程化”,编写专门的数学延伸课程,供不同层次的学生阅读与开展活动所用。让数学史料成为提升学生数学素养的不竭源泉。
(浙江省杭州市萧山区所前二小 311200)

