复合断面渠道水力最佳断面的选择

赵倩辉

(四川大学水利水电学院水利水电工程系，成都，610225)

复合断面渠道水力最佳断面的选择

赵倩辉

(四川大学水利水电学院水利水电工程系，成都，610225)

根据水力最佳断面基本概念，推求复合断面渠道水力最佳断面的计算公式，把公式运用到实践，达到工程经济合理的目的。

复合断面渠道 水力最佳断面

水力学教科书中介绍了梯形断面及矩形断面渠道的水力最佳断面的计算方法。但在实际工程应用中，由于渠道线路较长，沿线地形、地质条件的变化，经常会出现不同坡比的复合断面渠道(如底部为梯形、上部为矩形构成的复合断面渠道)。为便于在工程中选择这种复合断面渠道的水力最佳断面，本文根据水力学原理推求复合断面渠道的水力最佳断面计算公式，为渠道工程设计提供技术帮助。

1 水力最佳断面设计

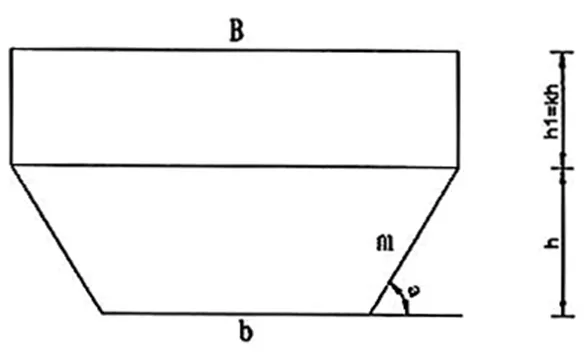
图1 复合断面

如图1所示，底部梯形断面底宽为b，高为h，边坡系数为m(m=cota)，上部矩形断面高为h1并假设h1=kh，长为B(B=b+2mh1)。

把曼宁公式代入明渠均匀流的基本公式，可得：

(1)

由式(1)可知，当渠道的底坡i，粗糙系数n及过水断面积A一定时，湿周x越小通过流量Q越大；或者说当i、n、Q一定时，湿周x越小所需的过水断面积A也越小。

工程中常用的断面形式是梯形断面，其边坡系数m由边坡稳定要求确定。在m已定的情况下，同样的过水面积A，湿周的大小因低宽与水深的比值b/h而异。根据水力最佳断面条件：

即

而A=B·h1+(b+mh)·h

A=(b+2mh)kh+(b+mh)h=bh(1+k)+2mkh2+mh2

(2)

(3)

(4)

(5)

将式(4)代入式(5)，可得：

整理可得：

(6)

由式(6)可以看出，此种复合渠道水力最佳断面的宽深比与边坡系数m，矩形断面高度h1与梯形断面高度h之间的比值k有关。

(7)

将b=βh代入式(7)，可得：

(8)

将式(6)代入式(8)，可得：

(9)

从上面公式可以看出，复合渠道的水力最佳断面必须满足式(6)的宽高比，此时的水力半径只和水深、高度比有关。

2 工程应用

某复合土渠底坡i、粗糙系数n及过水断面积A为15m2，试求水力最佳断面，并与一般断面进行比较。

水力最佳断面时β值应由式(6)确定。

从经济角度上来说，当渠道的底坡i、粗糙系数n及过水断面积A一定时，湿周x越小通过流量Q越大。

由表1，以水力最佳断面和一般断面进行比较，只有序号④中各项基础数据满足式(6)的条件。

表1 水力最佳断面与一般断面比较

3 结论

(1)求解这种复合渠道水力最佳断面，过去常采用试算法或图解法，虽然能得到正确答案但计算较复杂，工作量较大。现在有了成熟的理论公式，可以运用并指导实践；

(2)复合渠道的水力最佳断面宽高比必须满足式(6)的条件，此时的最佳水力半径只和水深h、高度比k有关。

〔1〕吴持恭.水力学[M].北京：高等教育出版社，2005.

〔2〕同济大学数学教研室.高等数学[M].北京：高等教育出版社，2007.

赵倩辉(1995.11-)，女，四川大学水利水电学院水利水电工程系学生。

■

TV

B

2095-1809(2016)04-0065-02