比例数据的拟似然推断及其应用
李泽安, 赵为华
(1.南通大学 计算机学院,江苏 南通 226019;2.南通大学 理学院,江苏 南通 226019)
比例数据的拟似然推断及其应用
李泽安1, 赵为华2
(1.南通大学 计算机学院,江苏 南通 226019;2.南通大学 理学院,江苏 南通 226019)
本文基于拟似然方法研究比例数据的统计推断及其在计量经济分析中的应用问题.拟似然估计不需要响应变量确切的分布假定,只需要一阶条件矩假设.与已有方法相比,本文提出的拟似然估计不仅具有稳健性而且具有很好的适应性. 最后,通过家庭食物消费数据分析充分说明了所提方法的有用性.
拟似然;比例数据;统计推断;食物消费
引 言
回归建模常用来揭示响应变量与一组协变量之间的相关关系,并根据得到的回归模型进行相应的统计推断,进而作出若干合理的预测分析,为决策者提供智力支持和决策依据.在实践中,我们经常碰到响应变量的取值在有限的区间[a,b]上.由于此类数据取值具有有界性特征,直接利用线性回归模型进行拟合分析往往是失效的,主要原因在于拟合值会超出区间的上下界. 另外,区间数据常常呈现出异方差性,使用基于同方差假定的最小二乘方法进行估计时会产生许多问题,且推断和预测的效果较差.再者,区间数据经常具有不对称性、多峰性等特点,此时基于对称误差分布的推断方法存在很大问题.

当因变量取值在开区间(0,1)时,亦称为连续型比例数据,已有一些文献对此展开过研究,如Peter和Tan(2000)[2]基于单纯形分布研究了连续比例数据的回归系数的估计及其推断问题;Ferrari和Cribari(2004)[3]通过对Beta分布进行参数变换,提出了Beta回归模型并借鉴广义线性模型的理论和方法研究了系数的估计及其统计诊断问题;李泽安等(2009)[4]应用Beta回归模型研究数据挖掘问题;Zhao等(2014)[5]基于惩罚函数方法研究了Beta回归模型中重要变量的选择问题.然而,以上文献都是基于单纯形模型或Beta回归模型进行估计方析,本质上是基于参数回归模型的似然估计方法进行统计推断.众所周知,当参数回归模型假定正确时,参数的估计和推断效率较高,而一旦模型假定错误时,估计的准确性和统计推断效率将大打折扣,甚至会出现错误结论.另一方面,当因变量取值在闭区间[0,1]时,或半开半闭区间[0,1)、(0,1]时,此时亦称为半连续型比例数据,前面提到的Beta回归模型或单纯型回归模型都无法适用.为避免上述似然估计方法的弱点,本文基于拟似然方法研究比例数据的回归建模问题.本文所提方法不需要对响应变量的分布作出任何假定,只需要响应变量的一阶条件矩的假定,并通过柯西分布的逆分布函数连接条件均值与自变量的回归结构,其最大优点是所得的估计具有很好的稳健性.同时,本文提出的方法既能拟合连续型比例数据也能拟合半连续型比例数据,因而具有很好的自适应性.
1 比例数据的拟似然估计
假设(xi,yi)(i=1,…,n)是一组独立样本,其中xi=(xi1,…,xip)T∈Rp.假定响应变量的条件均值E(yi)=μi,i=1,…,n.
由于0≤yi≤1,因此0<μi<1.为建立条件均值与自变量之间回归关系,我们假设有一个单调递增函数G(·):(-∞,+∞)→(0,1)使得

(1)
其中β=(β1,…,βp)T是p维回归系数. 如果假定自变量中的第一个分量xi1≡1,则模型(1)中包含了常数项.
由于比例响应数据的条件均值形式上具有Bernouli变量的期望相同的形式,我们借鉴Bernouli似然函数,提出比例数据的对数拟似然函数为

(2)

图1 三种不同分布的连接函数图形

(3)

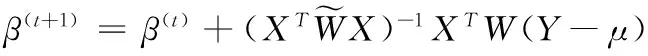
(4)


(5)
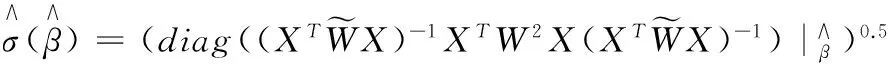
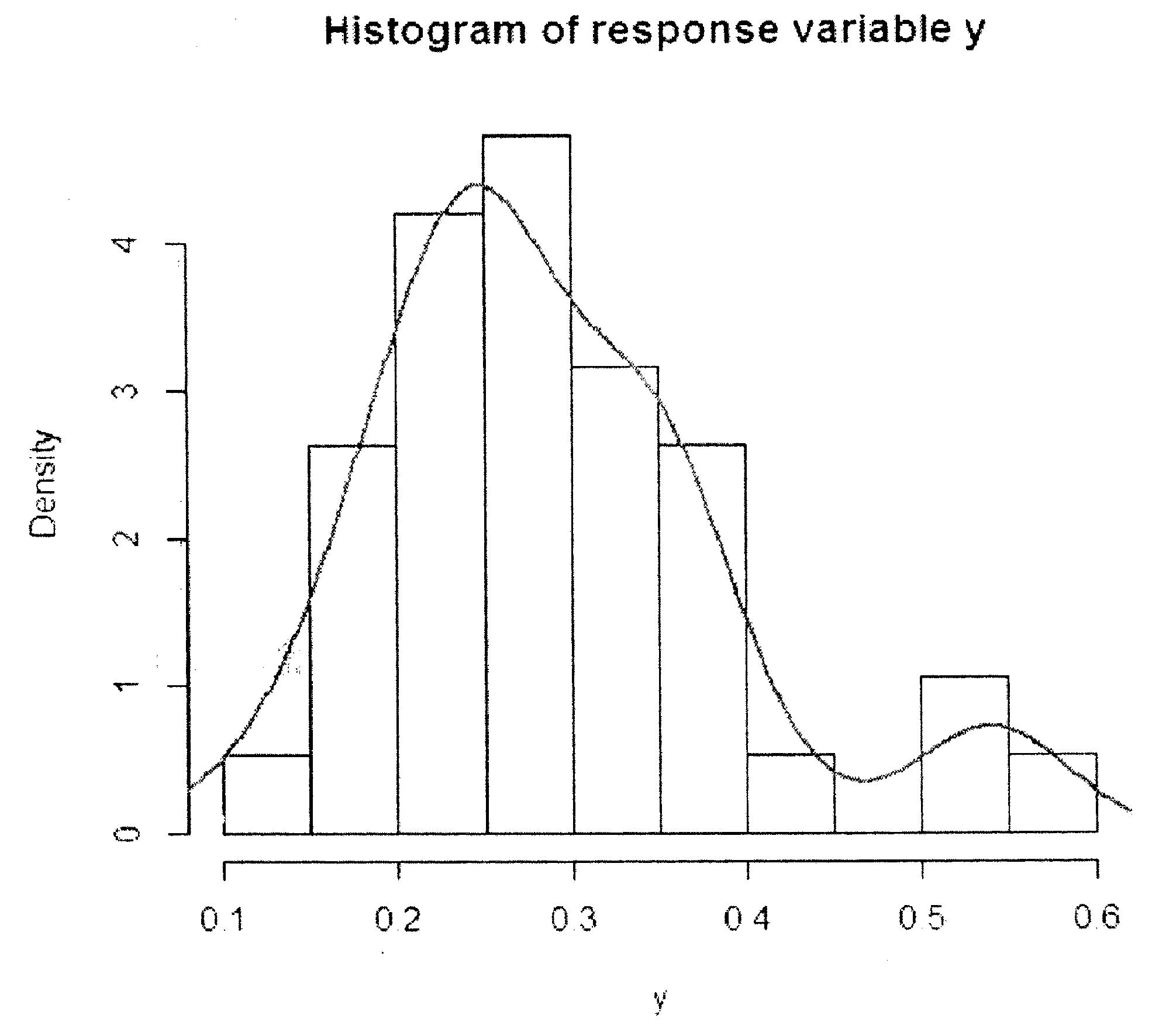
图2 响应变量的直方图及其密度曲线估计
2 实例应用
本节将拟似然估计方法应用到家庭食物消费数据(householdfoodexpendituredata) 分析中.家庭食物消费数据来自于计量经济学文献Griffiths等(1993)[7],研究者是从美国的某个大城市中随机调查38个家庭而得到的,统计学家或计量经济学家希望了解食物消费占家庭总收入支出比例情况,进而研究家庭的收入、家庭的人数与食物消费支出之间的动态相关关系. 该数据中含有两个自变量和分别表示某个该家庭的收入水平和该家庭成员的人数,响应变量是该家庭食物消费支出占整个家庭收入的比例,其直方图和核密度函数曲线估计见图2.
Ferrari[3]等(2004)曾利用Beta回归模型对此数据进行过拟合,这里我们使用拟似然方法再次研究该数据,即
G-1(μi)=β1+xi1β2+xi2β3,
i=1,…,38.
两种方法下的系数估计及其95%置信区间估计见表1.

表1 食物消费数据的回归系数估计
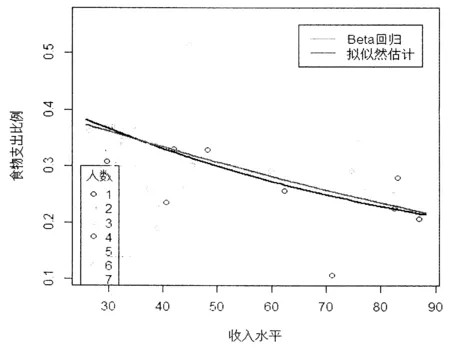
图3 收入水平与食物支出比例的散点图(不同颜色的散点代表家庭的不同人数)及其两种估计方法下的拟合曲线(在固定平均家庭人数).
从表1可以看出,两种方法下得到系数估计值具有相同的符号,且每一个变量在显著性水平0.01下是高度显著的.系数β2的估计符号都是负的,而系数β3的估计符号是正的,说明随着家庭人口的增加,整个家庭的食物支出比例在上升;同时,随着家庭总收入的增加,整个家庭的食物支出比例在不断下降.另一方面,在某个家庭中家庭人口固定的情形下,家庭收入越少,家庭收入中用来购买食物的费用所占的比例就越多,随着家庭收入的增加,家庭收入中用来购买食物的支出则会下降(参见图2),这完全符合实际情况,即计量经济学中的恩格尔定律.
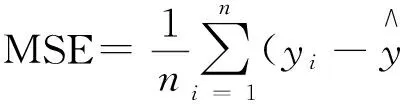
从表2和图3不难看出,无论MSE、MAD值的大小,还是拟合曲线与散点图的匹配程度,本文建议的拟似然估计方法明显地要比Beta回归来的好.这一点也可以从图 2中响应变量的直方图及其密度

表2 食物消费数据拟合的MSE和MAD
曲线估计看出,数据具有双峰性和厚尾性特征,很难使用Beta分布或其他参数分布进行较好地拟合.
为比较两种方法下的预测效果,下面我们使用交叉验证方法(cross-validation)计算预测偏差的绝对平均值(FAD)
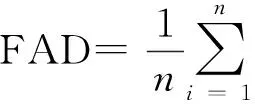
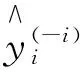
显然,本文提出的拟似然方法不仅在拟合偏差方面优于Beta回归,在预测能力方面也优于Beta回归.

表3 食物消费数据预测偏差FAD
4 总结
本文提出了使用拟似然方法研究比例数据的回归建模、估计、统计推断及其在计量分析中的应用问题.我们的方法既适用于连续型比例数据,也适用于半连续型比例数据.通过详细的实例分析,并与已有方法比较,充分说明了本文提出的比例响应数据拟似然方法的稳健性和自适应性.进一步的研究兴趣将讨论比例响应数据拟似然非参数、半参数建模方法及其理论分析和实际应用.
[1] KIESCHNICK R, McCullough, B. Regression analysis of variates observed on (0,1): percentages, proportions and fractions[J]. Statistical Modelling, 3:193-213,2003.
[2] PETER S, TAN M. Marginal models for longitudinal continuous proportional data[J]. Biometrics, 2000,56:496-502.
[3] FERRARI S, Cribari-Neto, F. Beta regression for modelling rates and proportions[J]. Journal of Applied Statistics, 2004,31:799-815.
[4] 李泽安,葛建芳,章亚娟.Beta回归模型在数据挖掘预测中的应用[J].南通大学学报,2009,8(3):83-85.
[5] ZHAO W, ZHANG R, LV Y, LIU J. Variable selection for varying dispersion beta regression model[J]. Journal of Applied Statistics, 2014,41:95-108.
[6] McCullagh P, NELDER J. Generalized Linear Models [M]. 2nd ed. London:Chapman and Hall, 1989.
[7] GRIFFITHS W, HILL R, JUDGE G. Learning and Practicing Econometrics[M]. New York: Wiley, 1993.
Quasi-Likelihood Estimation and Its Application for Proportional Data
LI Ze-an1, ZHAO Wei-hua2
(1. School of Computer, NanTong University, Nantong 226019, China;2. School of Science, Nantong University, Nantong 226019, China)
In this paper, we proposed the quasi-likelihood method to analyze the proportional data and its application in econometric modelling. Our proposed method does not need the distribution assumption for response variable, and only need the first order conditional moment assumption. Compared with existing method, the newly proposed estimation approach has both robustness and good adaptability in real data analysis. Finally, household food expenditure data analysis is used to illustrate the usefulness of the new approach.
quasi-likelihood; proportional data; statistical inference; food expenditure
10.14182/J.cnki.1001-2443.2016.06.004
2015-12-10
国家自然科学基金项目(11571112);教育部人文社科青年基金项目(14YJC910007).
李泽安(1977-),女,江苏南通人,讲师,主要从事数据挖掘方面的研究.
李泽安,赵为华.比例数据的拟似然推断及其应用[J].安徽师范大学学报:自然科学版,2016,39(6):526-529.
C81,O212
文章编号:1001-2443(2016)06-0526-04

