不完全权重信息下情报处理系统评估方法研究

郭清娥苏 兵张桂琴

（1．西安工业大学经济管理学院，陕西西安710032；2．中国人民解放军61112部队，黑龙江牡丹江157011）

不完全权重信息下情报处理系统评估方法研究

郭清娥1苏 兵1张桂琴2

（1．西安工业大学经济管理学院，陕西西安710032；2．中国人民解放军61112部队，黑龙江牡丹江157011）

情报处理系统给出的信息是决策者下一步行动的依据，因此情报处理系统的评估与优选对于任何决策者来说是至关重要的。根据不能准确获知指标权重的实际，构建不完全信息下情报处理系统评估方法。假设各评估系统均具有“使自身评价值最大化”的特点，求得各自的最优评估值和权重向量；借鉴DEA交叉评价的思想，各评估系统按照系统内所有方案的最有利权重进行评估后，将平均交叉评估值作为决策基准。

情报处理系统；不完全信息；部分权重信息；评估

情报处理系统的工作是指在情报收集基础上对各种情报进行二次处理，即分析、判断、整理、去伪存真、综合的过程，也即从获得情报到提供给决策者使用的整个过程。其目的是从局部零散的情报中挖掘出整体情况，为决策者提供较为客观、可靠的目标信息［1］。情报处理系统给出的信息是决策者下一步行动的依据，因此如何对情报处理系统进行准确的评估与优选，具有非常重要的意义。

情报处理是一项复杂的工作，整个过程充满不确定性，且受到众多因素的影响。考虑到其中大量非结构化、模糊性的因素，近年来国内外对情报处理系统评估，多采用模糊综合评价或灰关联分析方法。文献［2］利用影响情报处理系统效能主要因素指标的灰色特性，提出用灰色关联分析法作为系统效能评估的方法。文献［3］首先给出了正、负理想参考序列，在此基础上对各系统与其关联程度进行了计算，结合逼近于理想解的技术和灰关联分析技术，提出一种基于理想情报处理系统数据序列的灰色关联分析评估技术。文献［4］在灰色模糊评价法的基础上进行改进，利用层次分析法确定各因素的权重，但考虑了专家可信度，并用此方法对竞争情报系统的绩效进行评价。但这些方法在评估指标的确定上均采用完全由人为指定权重（即假设为已知）或采用AHP方法进行计算的方法，具有较强的主观性，很难排除人为因素带来的偏差。鉴于此，本文假定权重信息仅部分已知，借鉴DEA交叉评价思想，首先假设各评估系统均具有“使自身评价值最大化”的特点，求得各自的最优评价值和权重向量，在各评估系统按照系统内所有方案的最有利权重进行评价，将平均交叉评价值作为决策基准。最后结合情报处理系统评估的算例，验证了模型的可靠性和可行性，为决策者在情报处理系统评估实践提供新的参考视角。

1 问题描述

设情报处理系统评估问题中，X＝（x1，x2，…，xm）为情报处理系统的集合，U＝（u1，u2，…，un）为属性（评价指标）的集合，W＝（w1，w2，…，wn）T为属性的权重向量。W不完全已知，且部分权重信息的数学表达式通常由决策者给出，根据文献［5－6］，分为6类情形：（1）wi≥wj；（2）wi≥αijwj；（3）wi－wj≥βij；（4）γj≤wj≤ηj；（5）σij≤wi/wj≤ij；（6）wi＋wj≤2wk。i≠j≠k，其中αij，βij，γj，ηj，σij，ij为非负常数，这6类部分权重信息可能性集合记为Ω。A＝（aij）m×n表示评估矩阵，其中元素aij表示对于情报处理系统xi按属性uj进行测度得到的属性值。

本文要解决的问题即根据部分权重信息，对情报处理系统集合X中选择满意系统或对系统进行排序。

2 不完全权重信息下情报处理系统评估方法

2.1 评估指标的建立

评估指标的选择对评估来说非常重要。综合评估实际操作中，人们对评估指标的构建与筛选的方法包括德尔斐法、最小均方差法、极小极大离差法、相关系数法等［7］。情报处理系统是一个复杂系统，牵涉因素多、广，评估到底该考虑哪些指标，有文献进行了研究。但不同研究者因研究目的不同，至今并无定论。

2.2 建立原始决策评估矩阵

设X＝（x1，x2，…，xm）为情报处理系统的集合，U＝（u1，u2，…，un）为属性（评价指标）的集合，A＝（aij）m×n表示评估矩阵，其中元素aij表示对于情报处理系统xi按属性uj进行测度得到的属性值。A称为原始评估矩阵。将系统内所有指标分为效益型和成本型，其中效益型指标是指针对该指标来说，属性值越大越好；成本型指标是指针对该指标来说，属性值越小越好。

2.3 无量纲标准化处理

为了消除不同量纲对决策结果的影响，现采用“比重变换法”［8］将A规范化为A′。其计算公式为：

2.4 不完全权重信息下情报处理系统评估模型

对于属性未知或部分已知情况，在多属性决策研究中，已有文献将所有决策方案均采用一个权重标准来体现竞争公平性，较为粗糙。实际上这不利于发挥各决策方案的“积极性”。因此，本文假设评估的情报处理系统具有一定的“能动性”，各系统均具有“使自身评估值最大化”的“自利性”特点。也即，情报处理系统的评价值由下述规划给出：

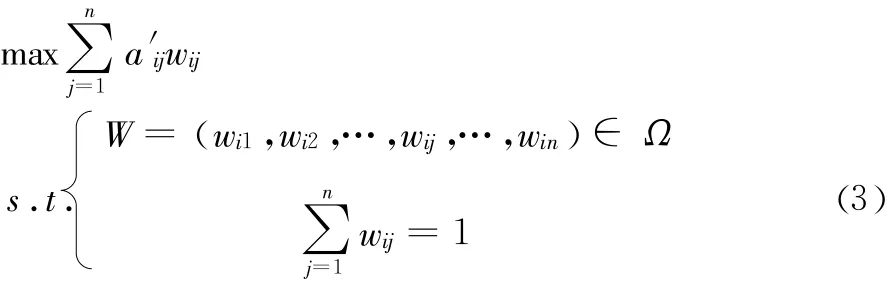
由（3）式，即可求得每一个情报处理系统的评估值，这也是它所能获得的最优评估值，此时的权重向量对该系统是最有利的。但由（3）表达式可知，该标准容易造成情报处理系统“夸大自身优势”、“回避自身缺陷”等问题。因此，本文借鉴DEA交叉评价思想方法，引入交叉评价的方式。

定义1称为情报处理系统案i对于系统k的交叉评估值，其中是规划方程（3）的最优解。

交叉效率vki表示当采用情报处理系统i的最有利权重时，系统k的相对评估值。即系统i对系统k的评估值。

定义2 称所有情报处理系统对系统i的交互评估平均值为方案i的平均交叉评估值，记为：

由定义及式（4）表达式可以看出，交叉评估值是将“自评”和“互评”相结合，客观全面的表现出各情报处理系统的优劣，更进一步体现了评估中的公平性。

依据式（3）求得每个情报处理系统xi的最优评估值及对应的最有利权重向量Wi；依据式（4）求得每个系统xi的平均交叉评估值根据平均交叉评估值对所有系统进行优选、排序。

3 实例应用

现有4个情报处理系统，拟根据本文提出的不完全权重信息下情报处理系统评估方法进行评估。

3.1 评价指标的建立

待评估的情报处理系统有4个，记为X＝（x1，x2，x3，x4），情报处理系统是一个复杂系统，情报处理过程牵涉面广、因素复杂。评估到底该考虑哪些指标，有文献进行了研究。通过对情报处理过程的考察及对已有文献的梳理与总结，本文的情报处理系统评估指标体系由该系统情报处理时延、该系统情报处理可靠性、该情报处理系统可修复性、该系统情报处理精度、该情报处理系统容量5个指标组成，即U＝（u1，u2，u3，u4，u5）＝（系统时延，系统可靠性，系统可修复性，系统处理精度，系统容量），其中系统时延u1为成本型指标，其余均为效益型指标。

3.2 建立原始评估决策矩阵

专家对情报处理系统评估得分如表1所示。

表1 各情报处理系统的评估指标得分

则由表1可得原始评估矩阵：

3.3 无量纲标准化处理

按照第三节的步骤，根据（1）、（2）对数据进行无量纲标准化处理，处理之后得到规范化评估矩阵：

3.4 不完全权重信息下情报处理系统评估

若已知部分权重信息为0≤w1≤0.3，0.3≤w2≤0.5，0＜w3≤0.2，0＜w4≤0.1，0＜w5≤0.2。利用规划（3），利用Lingo软件求得各情报处理系统最优评估值和对应的权重向量分别为：

3.5 分析与对比

为证明本文提出的评估方法的有效性，将文献［2］、［3］中的算例用本文所提出的模型评价并进行对比。文献［2］、［3］中的权重信息假设为完全已知，提前给出（权重向量为W＝（0.24，0.40，0.14，0.08，0.14）T）。恰好给出的权重向量在本文部分已知的范围附近。用本文模型计算各方案平均交叉评价值分别为：按照最终平均交叉评估值排序为：x2≻x1≻ x3。即情报处处理系统2最优，其次为系统1，最后为系统3。最终排序结果一致。可见本文给出的评估方法是有效的。

4 结 论

情报处理过程会受到很多因素的影响，且因人类认知能力有限性，有些因素的信息并不能完全被完全获取，以往多采用模糊理论或灰色系统理论进行评估，但对指标权重均假设完全已知。这并不完全符合实际情况。本文在评估过程中，假设权重信息只部分已知，假定情报处理系统具有一定的“能动性”，各系统均具有“使自身评估值最大化”的“自利性”特点，由此来确定指标权重；再借鉴DEA交叉评价的思想，各评估系统按照系统内所有方案的最有利权重进行评估后，将平均交叉评估值作为决策基准，最终得出了合理的排序结果，为情报系统评估提供了一定的参考与借鉴。

［1］魏云升，郭治，王校会．火力与指挥控制［M］．北京：北京理工大学出版社，2003．

［2］陈杨，王立平．灰关联分析在情报处理系统效能评估中的应用［J］．火力与指挥控制，2009，34（4）：153－155．

［3］周含冰，唐忠，刘东玉．基于理想解的情报处理系统灰关联评估算法［J］．计算机与数字工程，2013，41（1）：38－39．

［4］张翠英，张静．灰色模糊评价法在竞争情报系统绩效评价中的应用［J］．情报科学，2010，28（1）：81－85．

［5］Sexton T R，Silkman R H，Hogan A J．Data Envelopment Analysis：Critique and Extensions［M］．San Francisco：Jossey Bass，1986．

［6］王洁方，刘思峰，刘牧远．不完全信息下基于交叉评价的灰色关联决策模型［J］．系统工程理论与实践，2010，30（4）：732－737．

［7］张熠，王先甲．基于数据包络分析和模糊理论的投资项目评价方法研究［J］．技术经济，2010，29（2）：64－67．

［8］Goh C H，Tung Y C，Cheng C H．A revised weighted sum decision model for robot selection［J］．Computers&Industrial Engineering，1996，30（2）：193－199．

（本文责任编辑：马 卓）

Study on Evaluation Method for Intelligence Processing System with Incomplete Information

Guo Qinge1Su Bing1Zhang Guiqin2
（1．School of Economics and Management，Xi'an Technological University，Xi'an 710032，China；2．Troops 61112 of PLA，Mudanjiang 157011，China）

The evaluation and optimization of intelligence processing system is very important for any decision maker，because the information who gives is the basis of next action．Using the idea of DEA cross－evaluation for reference，the evaluation model for intelligence processing system under partial weight information was established．Assumed each of the system was selfserving to maximize its evaluation value and cross－evaluated others adopting weights which could compete for its goal；Integrated values of cross－evaluation results are used as decision criteria．And an example was given to illustrate the effectiveness of the method proposed．

intelligence processing system；incomplete information；partial weight information；evaluation

10．3969/j．issn．1008－0821．2016．02．008

TU723.2

A

1008－0821（2016）02－0043－03

2015－11－11

国家社会科学基金“城市交通拥堵形成机理及应对策略研究”（项目编号：13BGL156）；陕西高校人文社科青年英才支持计划；陕西省教育厅项目“基于合作博弈的中小企业银行柜面联盟研究”（项目编号：13JK0225）；西安工业大学校长科研基金“基于交叉评价及模糊综合评价的多属性决策方法”（项目编号：XAGDXJJ14016）。

郭清娥（1981－），女，讲师，博士，研究方向：评价与决策技术、应急管理与对策。