基于时间记忆的网络舆情意见交互模型研究
戴建华 廖瑞丹
(南京理工大学经济管理学院,江苏南京210094)
基于时间记忆的网络舆情意见交互模型研究
戴建华 廖瑞丹
(南京理工大学经济管理学院,江苏南京210094)
如何设计更符合实际情况的意见交互模型,使仿真研究结果更具真实性,是网络舆情仿真研究的核心问题。目前针对意见交互过程的多数研究仅考虑了邻居对意见形成的影响,忽略了以往符合遗忘规律的历史时刻个体意见态度对当前意见的“冲击”。本文在梳理、分析经典意见交互模型的基础上,考虑个体意见演变的时间记忆问题并结合卷积理论提出了新思路,建立基于HK模型的具有时间累积效应的意见交互规则模型,并给出算法实现。仿真研究结果表明:网络舆情中网民某时刻的意见值不仅受到当时周围邻居的影响,自身的历史记忆也对此产生作用。
交互规则;HK模型;卷积;时间记忆;仿真
随着互联网的不断发展,微博、论坛、博客等社交工具越来越普及,人们可以在网络上随意发表自己的言论,但是由于网络言论的匿名性,网民发言时不仅自由随意,而且泥沙俱下、鱼龙混杂。许多不满或失望的情绪很容易通过互联网这一渠道进行宣泄,网民从一开始的各抒己见到随意抒发不满或失望的情绪、再到通过互联网进行大肆的宣泄、互相攻击、谩骂等非理性现象十分突出,这些现象极大地妨碍了司法运行的正常秩序,对社会稳定也产生了不利的影响。因此,分析网络舆情的演变规律,尤其针对网民意见迁移的内在机理展开研究,建立更符合现实情况的意见交互模型,分析网络舆情的演变规律,进行网络舆情的预警预测,帮助政府更好地管理网络空间,成为当前网络舆论研究的热点。
目前,网络舆情演变的交互模型研究主要基于经典的选民模型(Voter Model)、多数统治模型(Majority Rule Model)[1-2]、Sznajd模型[3]、边界信任模型(Deffuant模型、HK模型)及其扩展,讨论了在规则网络和复杂网络两种交互环境下,网民意见的演变过程。例如:涂育松等人[4]改进了一维Sznajd的规则,得出意见演变依赖于初始意见分布和外界噪声强度的结论。王茹等人[5]基于二维[6]的Sznajd舆论模型探讨了不同初始状态中赞成个体密度对舆情演变结果的影响,认为舆情演变到一致反对和一致赞同的状态概率与初始赞成个体密度大小存在一定比例关系。苏俊燕等人进一步地考虑到人际之间的亲疏关系,基于加权网络上的Sznajd模型,研究加权网络的磁化率和权重(表示人际之间的亲疏关系)对舆论演化的影响[7],认为不同邻居对个体的影响程度不一样,使得个体不容易明确自己态度,权重越大越不利于一致意见的形成。
现实生活中个体的意见值不是“非此即彼”的二元情况,而是在某个区间上连续的。因此,以研究连续观点著称的有界信任模型[8]——HK模型和Deffuant模型被不断拓展。例如:陈桂茸等人提出了基于影响力和信任阈值、具有双重选择的意见交互模型[9],认为个体影响力和自我坚持度会影响舆论演化结果。杨雷等人[10]基于Deffuant模型,研究个体个性的意见交互规则,认为不同个性个体数量的变化对群体意见演化影响显著。
但是,近年来,对于仿真研究中的意见交互模型,无论是基于元胞[11]、HK、或者Sznajd[12]等基本模型还是修正模型[13]进行的演化仿真研究,个体在进行意见交互时,都仅被动地受到当前周围邻居的影响,而忽略了很多其他因素。基于此,本文拟结合信号处理中的卷积理论,引入时间记忆因素,不仅考虑周围邻居的当前意见值对其产生的影响,也将自身性格特点等纳入考虑范围,以期构建一个更符合现实情况的网络舆情演化过程中意见转变的交互模型。
1 具有时间记忆效应的意见交互模型的构建
HK模型是一个连续观点动力学模型,其观点的分布可以是[0,1]区间上的任意值,与Sznajd等二元观点和离散观点舆论模型相比,HK模型可以更好的反应个体对某个话题的赞同或反对程度,因此本文选择HK模型作为研究基础。
HK模型个体被动地受到周围邻居的影响,忽略了个体自身特点[14]对意见形成的作用。考虑到记忆对个体意见形成的促进关系,和信号与系统的相互作用表现得极为相似,本文提出了一种基于HK模型的意见交互卷积模型,将每一次记忆看作一次冲激,与当前个体的意见值卷积,得到受到时间累积影响的意见值,作为此刻个体的意见值。
1.1 卷积的物理意义及数学表达
1.1.1 卷积的物理意义
卷积的物理意义为信号和系统的相互作用[15]:系统的响应不仅与当前时刻系统的输入有关,也跟之前若干时刻的输入有关。之前若干时刻的输入信号经过一种过程(这种过程可以是递减,削弱,或其他)对现在时刻系统输出产生影响,计算系统输出时必须考虑现在时刻的信号输入的响应以及之前若干时刻信号输入的响应之“残留”影响的一个叠加效果。
1.1.2 卷积的数学表达
卷积的数学表达式为:
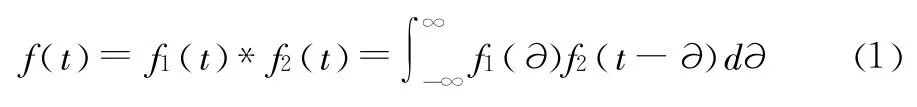
其中,f(t)是对f2(t)翻转、平移,然后与f1(t)相乘,再取分段积分的结果[16-17]。
1.2 具有时间记忆效应的意见交互模型
1.2.1 基本HK模型
在HK模型中,个体的意见交互对象是与其意见差异处于信任阈值范围内的邻居个体,个体下一时步的意见为交互对象意见的算术平均值[18]。
假设在某个连续边界的二维网络中有N个个体做随机运动,其中个体i拥有在区间[0,1]上的连续意见值,xi(t)表示在t时刻i的意见值;xj(t)表示在t时刻邻居个体j的意见值;在t+1时刻,i的意见是为所有属于信任集I(i,x)的个体意见的平均值,即:

1.2.2 意见交互的HK卷积模型
(1)在初始时刻,所有个体的意见值均为随机值,此时时间累积量为零,个体意见完全受到周围邻居影响。随着时间推移,时间记忆效应逐渐体现作用。本文为了体现整体演变趋势以及避免特殊情况出现,取个体意见平均值演化趋势进行分析。
假设整个意见交互过程处在一个连续的线性系统中,意见的形成过程是该系统的一个激励y(t),结果为它的响应f(t)。若假设系统已处于稳态,其响应就为零状态响应,即此时并没有受到历史记忆影响。
把在单位冲激δ(t)(个体对当前时刻t之前每一时刻个体的意见值的记忆效应)作用下的系统响应记做是h(t),即h(t)=T[δ(t)]。h(t)(此前每一时刻意见值对下一时刻意见形成的影响)反映了线性不变系统的特征,由δ(t)的筛选特性,可以得出:

可见,线性时不变连续系统的响应f(t)是激励y(t)和冲激响应h(t)的卷积分。即下一时刻个体的意见值为此刻未考虑时间累积因素的意见值与之前时刻个体意见值对下一时刻意见值形成影响的卷积分。
上式可以表示为离散形式:

其中,T为时间间隔,N为累积的次数。展开得:
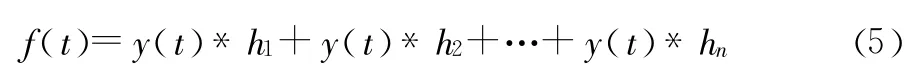
当y(t)和h1卷积时,表示历史记忆中距离当前时刻最近的时刻点对个体意见值的影响;当y(t)和h2卷积时,表示历史记忆中距离当前时刻为两个时刻间隔对个体意见值的影响,依此类推。
(2)认知科学研究认为,人脑记忆和遗忘是相辅相成的,所有信息在神经系统触发后就都会进入遗忘过程[19-20],艾宾浩斯提出了记忆曲线,揭示了遗忘“先快后慢”普遍规律。人脑不能将所有时刻点的意见都记忆得非常清楚,距离当前时刻越近的意见对当前意见形成的影响越大。
为了定量的描述记忆过程,多位学者用数学模型拟合该曲线[21-23]。易非易对艾宾浩斯曲线上的点进行指数回归分析,利用指数函数建立了单次记忆的记忆函数,拟合后的函数表达式为:
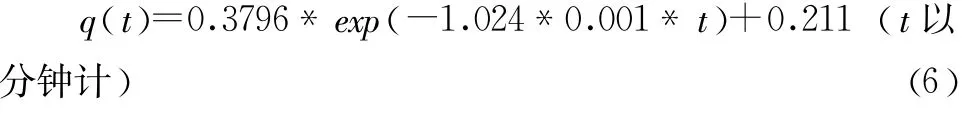
将q(t)简化,得到:
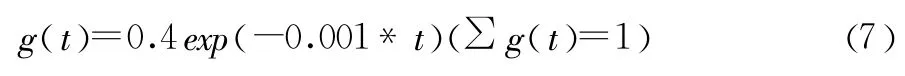
当前时刻t之前每一时刻个体意见值对下一时刻意见值形成的影响不同。考虑到个体记忆的特点,将g(t)与当前每一时刻点意见值的乘积作为个体能够记忆清楚的历史意见值对下一时刻意见形成的影响。

2 具有时间记忆效应的意见交互仿真
本文采用MATLAB R2014a软件进行仿真实验。在模拟过程中,网络中的个体根据上述模型规则进行意见交互。通过仿真得到未考虑时间记忆效果及考虑了时间记忆效应的意见平均值变化曲线,并对两条曲线进行对比分析。
2.1 仿真准备
2.1.1 交互邻居范围
为了表示现实生活中人与人之间的地理距离及有限的交际能力,假设在网络中,个体仅与周围邻居交互,定义函数d(i,j,t),表示t时刻个体i和邻居个体j之间的距离,个体i的邻居集合Neighborsi(j,t)定义为:

2.1.2 信任阈值ε
在HK模型中,信任阈值参数ε是一个实数,它限定了个体间可以产生意见交互的最大意见差异。
假设Neighborsi(j,t)的元素个数为m,根据信任阈值ε来确定参与意见交互的邻居个体集合J(j,t):
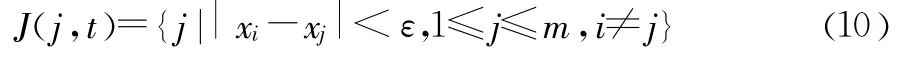
集合里的成员会随时间变化而发生改变。
2.1.3 信任程度w
信任分为对自身的信任(也可以理解为倔强度),及对其他个体的信任。
设定一个信任度参数wii来表示个体i对自身的信任程度,wii值越高,个体越自信,越不容易被其他个体影响。
此外,现实生活中个体之间的熟悉程度、以及个体自身的性格特点等,使个体对他人信任程度不同。这种人与人之间的信任程度可以抽象为信任度参数wij,即个体i对周围邻居j的信任程度[24]。
假设个体i拥有若干邻居,k是信任集合J(j,t)中元素的数量,可以得到:

基于基本HK模型,可以得到:

其中,y(t+1)为仅受到邻居yj(t)影响的意见形成结果。
2.2 HK卷积模型仿真
由于信任阈值越小收敛速度越慢,为了更好地观察网络中所有个体的意见值每一个时刻的平均值变化,选择信任阈值较小(ε=0.3)的情况对HK卷积模型进行仿真。
选用2 500个随机个体进行演化。演化200步,使最终系统收敛到一个稳定的状态。
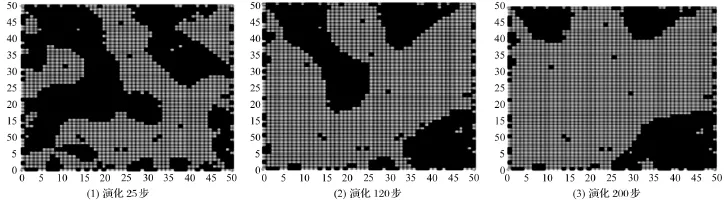
图1 演变过程
从图1可以看到,处于初始分散状态的格子经过逐渐演化,相同颜色的格子聚集到一起,且黑色格子的数量明显减少。
2.2.1 未考虑时间记忆效应的情况
根据演变过程,画出意见平均值的变化情况,个体意见平均值保持在0.5左右,仅有缓慢的上升趋势,并没有发生明显的极化现象。
使用MATLAB拟合工具箱,对图2的意见平均值变化曲线进行拟合。拟合后的结果如图3所示。
拟合后意见平均值变化曲线的函数表达式为:
y(t)=0.4857*t^0.1238(13)2.2.2 考虑了时间记忆效应的情况
根据1.2.2小结中HK卷积模型,对图3拟合后的意见平均值曲线进行卷积。
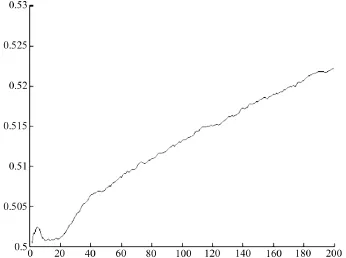
图2 意见平均值变化
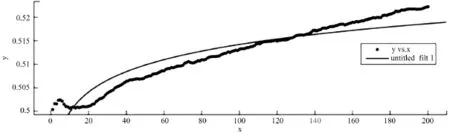
图3 拟合意见平均值变化
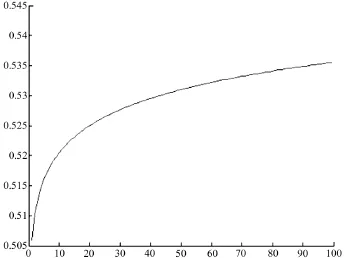
图4 卷积后的意见平均值变化
从如图4可以看出,卷积后意见平均值的变化整体趋势与卷积之前的意见平均值变化相同。但是卷积后的曲线,收敛的更快,更快地到达一个稳定值。
2.3 结果分析
(1)个体经过HK模型的演变规则演化之后,系统中意见相近的个体发生交互,意见值相近但是持不同意见的个体可能会被持其他意见的个体同化。即在现实生活中,人们经过意见交流之后,会使自己的意见向周围意见相近的邻居意见靠拢。
(2)时间积累效应能够延缓或加速某时刻的意见形成。如果某个人在当前时刻之前的时刻持有的意见持续为赞成,但是这段时间周围能对他产生影响的人持有的意见都是反对,那么这个人由于时间积累效应会延缓将意见由赞成改变为反对。如果某个人在当前时刻以前的时刻持有的意见持续为赞成,而且这段时间周围能对他产生影响的人持有的意见都是赞成,那么这个人由于时间积累效应将会加速将意见的赞成程度加深。
3 结 论
意见交互模型是网络舆情演变过程研究的核心问题。本文通过对国内外文献资料的研究,发现现阶段研究多数仅考虑外界周围邻居对意见形成的影响,忽略了人类具有的主观性,即很少考虑过去时刻个体的意见态度对现在意见形成的影响。本文将时间记忆因素引入到意见交互模型中,考虑个体意见演变的时间累积问题,利用卷积理论建立基于HK模型的具有时间积累效应的意见交互模型,并使用MATLAB软件对模型进行仿真实现。得到意见转变不仅受到周围邻居影响,自身历史记忆也将对决策起到一定作用的观点。为网络舆情演变中意见交互研究提供新思路。
[1]刘云,丁飞,张振江.舆论形成和演进模型的研究综述[J].北京交通大学学报,2010,(5):83-88.
[2]Galam S.Contr ar ian Deterministic Effects on Opinion Dynamics:the Hung Elections Scenario[J].Physica A,2004,333:453-460.
[3]Katarzyna Sznajd-Weron,Jozef Sznajd.Opinion evolution in closed community[J].Int.J.Mod.Phys.C,2000,11(6):1157-1165.
[4]涂育松,李晓,邓敏艺,等.一维Sznajd舆论模型相变的研究[J].广西师范大学学报:自然科学版,2005,(3):5-8.
[5]王茹,蔡勖.推广小世界网络上的Sznajd舆论模型[J].广西师范大学学报:自然科学版,2008,(1):7-10.
[6]刘慕仁,邓敏艺,孔令江舆论传播的元胞自动机模型(1)[J].广西师范大学学报:自然科学版,2002,20(6):1-4.
[7]苏俊燕,孔令江,刘慕仁,等.加权网络上Sznajd舆论模型研究[J].广西科学,2008,(1):44-46,51.
[8]张伟,何明升,白淑英,等.基于Weisbuch-Deffuant模型的网络舆论演化模式研究[J].情报杂志,2013,(7):43-48.
[9]陈桂茸,等.网络舆论演化的高影响力优先有限信任模型[J].上海交通大学学报,2013,47(1):155-160.
[10]杨雷,习鹏.决策者个性混合群体观点演化的仿真[J].工业工程,2011,(2):23-27.
[11]王根生,勒中坚.小世界效应的网络舆情演化迁移元胞模型[J].小型微型计算机系统,2011,(12):2523-2528.
[12]潘新.基于复杂网络的舆情传播模型研究[D].大连:大连理工大学,2010.
[13]P.Chen and S.Redner Majority Rule Dynamics in Finite Dimensions Phys.Rev.E 71(2005)036101.
[14]朱军芳.网络上集体行为的动力学研究[D].合肥:中国科学技术大学,2010:56-57.
[15]崔彩霞,胡学文,张帆.离散信号卷积的简便运算方法[J].兰州工业高等专科学校学报,2005,(1):48-51.
[16]付会凯.卷积积分运算方法探讨[J].黑龙江科技信息,2008,25:5.
[17]李泽涛.卷积与相关的比较研究[J].涪陵师范学院学报,2005,(5):75-77.
[18]于春龙.网络环境下群体决策的动态演化研究[D].南京:南京理工大学,2014.
[19]陈月,解焱陆,周照莲,等.基于卷积记忆模型的汉语知觉训练分析[A].中国中文信息学会语音信息专业委员会、中国声学学会语言、听觉和音乐声学分会、中国语言学会语音学分会.第十二届全国人机语音通讯学术会议(NCMMSC'2013)论文集[C].中国中文信息学会语音信息专业委员会、中国声学学会语言、听觉和音乐声学分会、中国语言学会语音学分会,2013:6.
[20]袁铁柱,王磊.基于记忆模型的两阶段Web服务发现算法[J].计算机工程,2010,18:250-252.
[21]易非易,任力锋,谢嘉平.学习与记忆模型研究[J].数理医药学杂志,1997,10(2):105-108.
[22]江志恒,刘乃芩.论遗忘函数——关于记忆心理学的数学讨论[J].心理学动态,1988,(3):56-60.
[23]张格伟,胡建,俞烽,等.支持遗忘特征的记忆模型及其在知识管理中的应用[J].信息与控制,2008,(5):621-626.
[24]李澍淞.基于蜂拥策略的网络舆论演化模型研究[D].上海:复旦大学,2011.
(本文责任编辑:孙国雷)
Study on Transformation of Public Opinion Study on accumulation Time
Dai Jianhua Liao Ruidan
(Institute of Economics&Management,Nanjing University of Science&Technology,Nanjing 210094,China)
How to design the opinion interactive model in line with the actual situation,makes the simulation results more authentic,is the core problem of network public opinion research simulation.The major research of international opinion process is only considered the influence of the neighbor to the formation of the opinion,neglecting the impulse of individual opinion attitude towards the current comments on the historical moments.Based on carding,analyzing the classical opinion interactive model,considering the time memory problems of individual opinion evolution,combining the convolution theory to establish the opinion rules of interaction model with time cumulative effect based on HK model,and implementing the algorithm.The results of the simulation show:In a moment of netizen opinion value of network public opinion is not only affected by the surrounding neighbors at the time,its own historical memory will also play an important role in.
rules for the interaction;HK model;convolution accumulation;time memory;modeling and simulation
10.3969/j.issn.1008-0821.2016.02.002
G206.2
A
1008-0821(2016)02-0008-04
2015-06-11
国家自然科学基金项目“突发事件网络舆情演变过程中的人群仿真研究”(项目编号:71273132)。
戴建华(1969-),女,副教授,博士,研究方向:决策分析、管理决策。

