颗粒级配对粗粒土强度与变形特性影响的研究*

陈 铖刘小清罗正东宁志强

（①湘潭大学土木工程与力学学院 湘潭 411105）

（②岩土力学与工程国家重点实验室，中国科学院武汉岩土力学研究所 武汉 430071）

颗粒级配对粗粒土强度与变形特性影响的研究*

陈 铖①②刘小清①罗正东①宁志强①

（①湘潭大学土木工程与力学学院 湘潭 411105）

（②岩土力学与工程国家重点实验室，中国科学院武汉岩土力学研究所 武汉 430071）

采用三维颗粒流软件PFC3D的内置FISH语言，进行二次开发，模拟粗粒土级配，建立一个研究高铁填方路基粗粒土变形特性的颗粒流模型。通过粗粒土三轴试验，标定了表征粗粒土细观力学性质的模型参数，并验证了模型的有效性。考虑粗粒土曲率系数和不均匀系数对颗粒级配的影响，模拟并研究了5种不同级配下粗粒土在3种不同围压下的变形特性。试验结果表明，曲率系数对粗颗粒土变形特性影响较大，当其有效粒径与中值粒径及限制粒径的差距过大时，粗粒土中颗粒填充及致密性将变差，变形增大，强度降低。以较大曲率系数与较大不均匀系数组合的粗粒土受力性能较好，但此种级配的粗粒土压缩性大。级配良好且不均匀系数较大，其应力链分布越均匀，颗粒的挤压效果越显著，力的传递和分配也越均匀。

粗粒土 曲率系数 不均匀系数 应力链

0 引 言

粗粒土泛指冲洪积砂卵石、采挖堆石、砾质土以及各种软岩分化料。目前，在高速铁路填方路基中，填料一般采用粗颗粒填料。根据郭庆国（1998）在文献中的结论，粗颗粒是指粒径5mm以上的颗粒。几十年来，专家学者们对粗粒土的强度、应力－应变关系、复杂应力状态下的力学表现做了重点研究，但基本上都习惯于借助传统的室内试验来研究粗粒土的强度及变形特性。Ahad et al.（2009）研究了粗粒土最大粒径对抗剪强度的影响；秦红玉等（2004）通过三轴试验研究了粗粒料中不同泥岩含量对堆石坝粗粒料强度的影响；张嘎等（2004）对粗粒土与结构接触面在循环荷载作用下的力学特性进行了系统的试验研究，讨论了循环荷载作用下接触面受力变形的规律和机理；程展林等（2007）通过CT三轴试验，从细观角度研究了粗粒土颗粒之间的相互作用以及颗粒的相对位置对其强度及变形性质的影响；姜景山等（2009）通过大型三轴压缩试验研究了密度、围压对粗粒土力学性质的影响，并分析了围压对应力－应变曲线的影响；冯大阔等（2009）通过实验研究，分析了粗粒土与结构的接触面间的相互作用现象，总结了在常刚度法向边界条件下两者相互作用的基本规律；周健等（2013）利用空心圆柱仪对砾石土进行三轴压缩、扭剪、三轴－扭剪联合3种单调加载路径试验以及应力主轴旋转路径试验，研究了应力路径对砾石土力学性质的影响；邓国栋等（2014）采用大型动三轴仪对高速铁路路基粗粒土填料进行实验研究，分析应力水平、固结围压、振动频率以及振动次数对动弹性模量和阻尼比的影响。同时，一些学者通过改变粗粒土中某颗粒级配段粗粒的含量来研究粗粒含量对粗粒土力学及变形性质的影响。王瑞甫（2014）利用单轴压缩蠕变试验，探讨粗粒土中细颗粒含量与蠕变参数之间的关系。石熊等（2014）通过向素土中掺加不同比例的碎石，对改良后的高铁路基粗粒土进行大型三轴剪切试验，结果表明级配改良后的粗粒土压实特性显著提高，各主要检测指标也有较大幅度的提高。进入21世纪，离散元方法被国内学者引入来研究岩土材料的力学性质。耿丽等（2011）通过室内试验，基于三维离散元颗粒流理论，从细观角度出发，得到按级配生成的粗粒土三轴试验的颗粒流数值模型，通过对不同围压下颗粒流模型与室内三轴试验的力学关系曲线的对比，研究了影响粗粒土强度的颗粒细观参数；徐肖峰等（2013）通过大型直剪试验和离散元模拟方法研究了粗粒含量对粗粒土宏观及细观性质的影响机理；董辉等（2015）采用颗粒离散单元方法，对影响堆积碎石土宏观变形特征的细观参数进行虚拟试验敏感度分析。粗颗粒填料的选择优化是高速铁路填方路基工程建设中的关键技术之一，而颗粒级配优化又是粗颗粒填料选择优化中的重要一项。进入21世纪，颗粒流数值方法被引入我国，越来越多的学者用这一方法来研究岩土的力学性质，特别是在对砂土、黏性土及堆石体的研究方面取得了不少的成果，但是利用颗粒流数值方法对高铁路基粗粒土力学性质的研究并不多见，尤其是利用离散元法研究颗粒级配对高铁路基粗粒土受力及变形性质的研究尚属少见。

本文选取武广高铁湖南境内某地区的铁路路基粗粒土进行了室内大型三轴试验，利用离散元方法，借鉴前人建立颗粒流模型的经验，建立一个三轴试验模型，该颗粒流模型能够较好地模拟粗粒土室内三轴试验时的力学表现。在此基础上，重新编程，开发出一种级配生成程序，利用该程序能使生成的粗粒土颗粒流模型的颗粒级配与室内试验的颗粒级配一致，并且能够根据需要生成任意指定级配的粗粒土模型试样。参考室内三轴试验结果，标定了粗粒土颗粒流模型的细观模型参数，验证了模型的有效性。采用标定的细观参数，研究颗粒级配对高铁路基粗粒土强度与变形性质的影响，为高铁路基粗粒土级配选择提供一定依据，也为研究粗颗粒填料在动荷载作用下的力学表现奠定了一定基础。本文假定不考虑颗粒破碎以及颗粒形状，用球形颗粒模型代表粗粒土颗粒。

1 试验方案与结果分析

1.1 试验方案

本文中大型三轴实验的原料是粗粒土，选自武汉—广州高速铁路湖南段某铁路填方路基的粗粒土填料。圆柱形三轴试验试样高度H＝645mm，直径D＝254mm，粗粒土颗粒粒径范围为5～38mm。该实验为排水实验，径向变形通过绑设在距试样两端1／3及1／2高度处的3个测量仪器测得，径向变形取3个量测值的平均值，体积变形由轴向变形和径向变形算得。试样直径和最大颗粒粒径比为6.68，试样尺寸与平均颗粒半径之比为60.09。根据刘海涛等（2009）的结论：当试样尺寸与平均颗粒半径之比大于40时，试样尺寸对粗粒土抗剪强度没有影响。根据中华人民共和国国家发展与改革委员会（2007）规定，试样直径与试样中最大颗粒粒径之比不应小于5，试样尺寸的选取消除了尺寸效应对试验结果的影响。试样级配曲线（图1）。

图1 颗粒级配曲线图Fig.1 Grain size distribution curve

本文采用偏应力q和静水应力不变量p来描述材料的应力-应变关系。应力、应变变量如下所示：

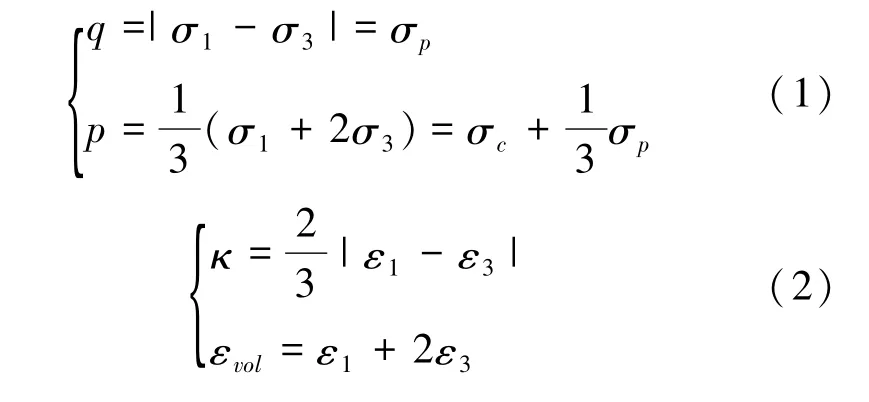
1.2 试验结果分析

室内大型三轴实验结果（图2），当围压分别为10.3kPa、41.3kPa、68.9kPa时，试件的应力比－q／p与偏应变κ、体应变εvol与偏应变κ的关系曲线具有相同的走势。如图2a所示，随着偏应变的增加，应力比值增大，最终趋于稳定，偏应变在0％～1％的范围内，应力比增加很快，偏应变在1％之后，应力比的增幅几近于零。不同围压下的应力比－偏应变曲线的形状走势相同，随着围压的增大，应力比－偏应变曲线的稳定峰值降低。从图2b可以看出，围压对试样体应变的变化幅度有影响：围压越大，体应变的变化幅度越小。在偏应变κ增加的过程中，粗粒土变形由剪缩变形转为剪胀变形，随着围压的增大，粗粒土剪缩变形段所对应的偏应变κ范围变大，即体积变化变缓。

图2 室内试验的应力比－偏应变、体应变－偏应变关系曲线Fig.2 Stress-strain curves in indoor testa.应力比－偏应变曲线；b.体应变－偏应变曲线

2 颗粒流数值模拟研究

2.1 数值模型生成过程

编写程序，生成符合试验土样颗粒级配的数值模型。首先，将级配曲线分段，得到分段点的粒径及对应的质量累计百分数，两个分段点对应的质量累计百分数差即为粒径区间段土样占整个土样的质量百分数。然后，分段生成。基本土粒的密度相同，质量含量即是体积含量，以体积量为控制参数，以类似半径膨胀法的方法随机生成每个区段所对应的土体颗粒，这些颗粒的位置可以重叠。最后，基于动力学基本原理，运行程序，颗粒相互排斥充斥整个空间形成土样模型。级配生成法的基本过程如图3所示，最终生成的是符合试验土样颗粒级配的颗粒流数值模型，其中相同级配段的颗粒用同种颜色表示，此模型尺寸与室内试验一致，高645mm，直径254mm。

耿丽（2011）分析了颗粒流细观参数对粗粒土强度的影响，标定了粗粒土三轴试验模型的细观参数，本文参考了其标定方法及徐金明等（2010）标定细观参数的方法。首先调节摩擦系数，通过与试验曲线比较，确定数值模型的强度峰值；然后通过调整法向切向刚度比，通过数值拟合的方法，进一步标定与室内三轴试验结果相对应的细观参数；最终选取一组最能成功拟合室内试验结果（图4a）的细观参数（表1）。颗粒流数值模拟的结果与室内三轴试验结果相比，前者应力比最大值之差为后者应力比最大值的0.5％，稳定后两者应力比值基本相等。同时，对比两者的体应变和偏应变的关系曲线（图4b），两条曲线走势一致，基本吻合，数值模型的有效性和细观参数的可靠性得到验证。

表1 颗粒流数值模拟参数设置表Table 1 Numerical simulation of particle flow parameters

表2 数值模型级配信息表Table 2 Information of grain size distribution of numericalmodels

图4 不同围压下颗粒流数值模型应力比－偏应变、体应变－偏应变曲线Fig.4 Stress-strain curves under different confining pressures in numericalmodelsa.应力比－偏应变曲线；b.体应变－偏应变曲线

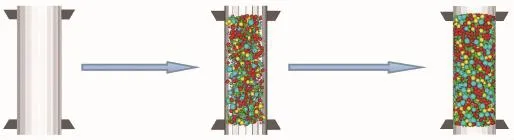
图3 级配生成法生成模型过程Fig.3 Process of generatingmodel with distribution generation method

2.2 不同颗粒级配下，粗粒土强度特性的颗粒流模拟分析

采用2.1节的模型生成方法以及标定的细观参数，生成其他4种不同级配的粗粒土颗粒流数值模型，其级配信息见表2，生成的颗粒流模型（图5）。其中，样本1代表的是2.1节所描述的室内三轴试验的颗粒流模型，每种颜色代表一段级配，此5个样本的模型尺寸和颗粒粒径范围与室内试验一致。样本生成后，选取3种不同的围压（10.3kPa、41.3kPa和68.9kPa）进行常规三轴压缩试验的颗粒流模拟。计算结果如图6、图7、图8所示。

图5 不同级配的数值模型Fig.5 Numericalmodelswith different grain size distribution

图6 围压为10.3kPa，不同颗粒级配下材料的体应变－偏应变、应力比－偏应变关系曲线Fig.6 Stress-strain curves with different grain composition under confining pressuresσc＝10.3kPa

图7 围压为41.3kPa，不同颗粒级配下材料的体应变－偏应变、应力比－偏应变关系曲线Fig.7 Stress-strain curves with different grain composition under confining pressuresσc＝41.3kPa

2.3 不同颗粒级配下，粗粒土变形特性的颗粒流模拟分析

如图9所示，围压等于10.3kPa时，样本1两端的颗粒密集分布，位移带最长，说明样本1在两端加载板附近有较多小球产生了较大的运动，同样的加载条件下，样本1最易被压缩，故而加载初期样本1的体缩现象最为明显（图6a）。样本2的位移场分布最为稀疏且位移矢量模量较其他样本小，说明在加载过程中样本2的颗粒移动较小，比较能保持最初的颗粒组构，表现出较大强度，故而出现了如图6b所示的“强度赶超”现象。并且，粗粒土中颗粒位移场的分布规律遵从其不均匀系数的大小排列顺序，即样本2的位移场最为稀疏，随着不均匀系数的增大，样本中部位置颗粒的运动越活跃，位移场分布越均匀。粗粒土的颗粒模型中其颗粒位移场分布越均匀，说明颗粒的移动范围越大；位移场疏密程度越均匀，说明发生相互错动的颗粒范围越广泛，颗粒原先的结构越容易被改变，体变也越大。随着围压的加大，颗粒的位移场分布变得越均匀，在位移场中部，发生径向位移的范围变小，颗粒的轴向运动明显。并且由于围压的加大，颗粒移动变得困难，体变速率明显变小。从图9可以看出，样本1体现出较好的受力性能，样本5体现出较大的压缩性，表明较大曲率系数（1、3之间，靠近3）与较大不均匀系数组合后粗粒土的强度越高，但是其压缩性也相应地增大。

图8 围压为68.9kPa，不同颗粒级配下材料的体应变－偏应变、应力比－偏应变关系曲线Fig.8 Stress-strain curveswith different grain composition under confining pressuresσc＝68.9kPa

图9 不同围压下，不同颗粒流数值模型中颗粒的位移场变化图Fig.9 Displacement field distribution of various numerical models under different confining pressures

从表2可以看出，样本3、4、5的有效粒径和中值粒径及限制粒径的差距较样本1、2大得多。有效粒径与中值粒径及限制粒径差距很大，表明土体中的细小颗粒所占比例较大。同一围压下，样本3、4、5的位移场较样本1、2均匀，围压加大，位移场分布越均匀，样本两端位移集中区域变小，说明颗粒相互错动明显，粗粒土容易发生体缩变形，其强度增高。细小颗粒占的比例过大，粒度分布连续性差，将会导致空隙空间分布‘不均匀化’，粗粒土中容易出现较大空隙，将不利于空隙的有效填充，不利于致密土颗粒骨架的构建，因此就出现了如样本4这样级配良好的粗粒土的强度和变形特性反而不如其他级配不良的样本。根据上述试验结果，在1和3之间，随着曲率系数的减小，可以近似得出粗粒土变形性能增强的结论。由此可知，要想得到较致密的粗粒土填料，有效粒径与中值粒径及限制粒径的差距不宜过大。

2.4 不同颗粒级配下，粗粒土颗粒间力链变化规律的颗粒流模拟分析

图10 不同围压下，不同颗粒流数值模型中颗粒间应力链的分布图Fig.10 Stress chain distribution of various numericalmodels under different confining pressures

图10 所示的是颗粒流模拟试验中颗粒间的应力分布图。其中，红色部分代表拉应力，黑色部分代表压应力，应力分布在几何上呈现链状分布，我们称之为力链。颗粒间应力的性质、强弱以及其分布状况在力链土中都能得到直观的体现。围压增加，模型试样的径向束缚加强，颗粒的径向运动的约束也相应的加强，在加载条件不变的情况下，颗粒的挤压程度将随围压的加大而加强，这一过程表现到力链图上就是围压加大，拉应力链减少，压应力链增加。在同一围压下，随着不均匀系数的增大，拉力链减少，压力链增多，且级配越接近良好级配条件，其力链分布越均匀，这说明级配越好，颗粒的挤压效果越显著，力的传递和分配也越均匀。

3 结 论

（1）采用颗粒流方法模拟分析了粗粒土的强度与变形特性，建立了符合材料真实级配曲线的颗粒流数值模型，通过与室内三轴试验结果比较，验证了本文所建颗粒流数值模型的正确性与有效性。该方法能够灵活改变试验条件，方便而有效地开展不同试验条件下的数值模拟。

（2）选取5种不同的颗粒级配，分别建立其相应的颗粒流模型，模拟分析了颗粒级配对粗粒土力学性质的影响：曲率系数对粗粒土的强度与变形特性影响较大，当其有效粒径与中值粒径及限制粒径的差距过大时，粗粒土中颗粒填充及组合致密性较差，强度与变形性能下降。

（3）通过颗粒流程序，分析了颗粒的运动变化规律和颗粒间应力链的变化规律，较好地描述了粗粒土的细观力学性质。随着围压的增加，颗粒位移场的分布变得均匀，在位移场中部，颗粒发生径向位移的范围变小，颗粒的轴向运动明显，体变速率降低。颗粒间压应力链逐渐增加，向更加密实的挤压状态转变。较大曲率系数（1、3之间，靠近3）与较大不均匀系数组合后粗粒土的强度与变形性能较好，但此种级配的粗粒土压缩性增大。不均匀系数增大，拉力链减少，压力链增多，且级配越接近良好级配条件，其力链分布越均匀，颗粒的挤压效果越显著，力的传递和分配也越均匀。

（4）本文的研究，没有考虑粗粒土颗粒形状的影响，而事实上粗粒土颗粒具有随机的形状，颗粒间除了存在摩擦力外还存在较大的“咬合”力。此外，在粗粒土颗粒接触处，由于颗粒形状不同，容易产生应力集中，会出现某点的接触力极大，颗粒受压产生破碎，颗粒破碎后，粗粒土中应力将产生重分布，势必也会影响粗粒土的强度与变形性质。所以，综合考虑颗粒破碎、颗粒形状以及颗粒级配的共同作用将是今后研究粗粒土细观力学性质的一个主要方向。

Ahad Bagherzadeh-khalkhali，Mirghasemi A A.2009.Numerical and experimental direct shear tests for coarse-grained soils［J］. Particuology，7（1）：83～91.

Cheng Z L，Ding H S，Wu L P.2007.Experimental study on mechanical behavior of granular material［J］.Chinese Journal of Geotechnical Engineering，29（8）：1151～1158.

Deng G D，Zhang JS，Wang Q Y，et al.2014.Experimental research on dynamic parameters of high-speed railway coarse-grained padding［J］.Journal of Railway Science and Engineering，2（11）：76～83.

Dong H，Ma Y Y，Fu H L，et al.2015.Particles discrete element simulation accumulation of gravel soil deformation parameter sensitivity analysis［J］.Chinese Journal of Computational Mechanics，32（2）：192～199.

Feng D K，Zhang G，Zhang JM，et al.2009.Experimental study on 3D cyclic behaviors of soil-structure interface under constant normal stiffness condition［J］.Chinese JournalofGeotechnical Engineering，31（10）：1571～1577.

Geng L，Huang Z Q，Miao Y.2011.Meso-mechanics simulation triaxial test of coarse-grained soil［J］.Journal of Civil Engineering and Management，28（4）：24～29.

Guo Q G.1998.The engineering properties and application of coarse grained soil［M］.Henan：The Yellow River Water Conservancy Press：6～9.

Jiang JS，Liu H L，Cheng Z L，et al.2009.Influences of density and confining pressure on mechanical properties for coarse grained soils［J］.Journal of Yangtze River Scientific Research Institute，26（8）：46～50.

Liu H T，Cheng X H.2009.Discrete element analysis for size effects of coarse-grained soils［J］.Rock and Soil Mechanics，30（S）：287～292.

Li JZ，Xu JM，Huang D Y.2015.Particle flow simulation of deformation and failure mechanism of granite based on actual distributions of meso-compositions［J］.Journal of Engineering Geology，23（S）：84～90.

National Development and Reform Commission.2007.Code for coarsegrained soil tests for hydropower and water conservancy engineering（DL／T5356—2006）［S］.Beijing：China Electric Power Press.

Qin H Y，Liu H L，Gao Y F，et al.2004.Research on strength and deformation behavior of coarse aggregates based on large-scale triaxial tests［J］.Rock and Soil Mechanics，25（10）：1575～1580.

Shi X，Zhang JS，Liu B，et al.2014.Test of high-speed railway course grained filler of improved particle size distribution［J］.Journal ofCentral South University（Science and Technology），45（11）：3964～3969.

Wang L F.2014.Experimental research on influence of content of fine particles on creep properties of coarse-grained soil［J］.Technology of Highway and Transport，1（5）：1～4.

Xu JM，Xie Z L，Jia H T.2010.Simulation ofmesomechanical properties of limestone using particle flow code［J］.Rock and SoilMechanics，31（S2）：390～395.

Xu X F，Wei H Z，Meng Q S，et al.2013.Dem simulation on effect of coarse gravel content to direct shear strength and deformation characteristics of coarse-grained soil［J］.Journal of Engineering Geology，21（2）：311～316.

Zhang G，Zhang J M.2004.Experimental study on cyclic behavior of interface between soil and structure［J］.Chinese Journal of Geotechnical Engineering，26（2）：254～258.

Zhou J，Wang Z H，Zhang J，et al.2013.Macro-meso research on mechanical behavior of a gravelly soil under various stress paths［J］. Chinese Journal of Rock Mechanics and Engineering，32（8）：1721～1728.

程展林，丁红顺，吴良平.2007.粗粒土试验研究［J］.岩土工程学报，29（8）：1151～1158.

邓国栋，张家生，王启云，等.2014.高速铁路粗粒土填料动力参数试验研究［J］.铁道科学与工程学报，2（11）：76～83.

董辉，马一跃，傅鹤林，等.2015.颗粒离散元模拟堆积碎石土变形的参数灵敏度分析［J］.计算力学学报，32（2）：192～199.

冯大阔，张嘎，张建民，等.2009.常刚度条件下粗粒土与结构接触面三维力学特性的试验研究［J］.岩土工程学报，31（10）：1571～1577.

耿丽，黄志强，苗雨.2011.粗粒土三轴试验的细观模拟［J］.土木工程与管理学报，28（4）：24～29.

郭庆国.1998.粗粒土的工程特性及应用［M］.河南：黄河水利出版社：6～9.

姜景山，刘汉龙，程展林，等.2009.密度和围压对粗粒土力学性质的影响［J］.长江科学院院报，26（8）：46～50.

刘海涛，程晓辉.2009.粗粒土尺寸效应的离散元分析［J］.岩土力学，30（增）：287～292.

李进昭，徐金明，黄大勇.2015.考虑细观组分实际分布的花岗岩变形破坏过程颗粒流模拟［J］.工程地质学报，23（增）：84～90.

秦红玉，刘汉龙，高玉峰，等.2004.粗粒料强度和变形的大型三轴试验研究［J］.岩土力学，25（10）：1575～1580.

石熊，张家生，刘蓓，等.2014.高速铁路粗粒土填料级配改良试验［J］.中南大学学报（自然科学版），45（11）：3964～3969.

王瑞甫.2014.细粒含量对粗粒土蠕变特性影响的试验研究［J］.公路交通技术，1（5）：1～3.

徐金明，谢芝蕾，贾海涛.2010.石灰岩细观力学特性的颗粒流模拟［J］.岩土力学，31（S2）：390～395.

徐肖峰，魏厚振，孟庆山，等.2013.粗粒含量对砾类土直剪过程中强度与变形特性影响的离散元模拟研究［J］.工程地质学报，21（2）：311～316.

张嘎，张建民.2004.循环荷载作用下粗粒土与结构接触面变形特性的试验研究［J］.岩土工程学报，26（2）：254～258.

中华人民共和国国家发展与改革委员会.2007.电水利工程粗粒土试验规程（DL／T5356—2006）［S］.北京：中国电力出版社.

周健，王子寒，张姣，等.2013.不同应力路径下砾石土力学特性的宏细观研究［J］.岩石力学与工程学报，32（8）：1721～1728.

STUDY OF STRENGTH AND DEFORMATION CHARACTERISTIC OF UNBOUND GRANUAL MATERIAL W ITH DIFFERENT GRAIN COMPOSITION

CHEN Cheng①②LIU Xiaoqing①LUO Zhengdong①NING Zhiqiang①
（①College of Civil Engineering and Mechanics，Xiangtan University，Xiangtan 411105）
（②State Key Laboratory of Geomechanics and Geotechnical Engineering，Institute of Rock and Soil Mechanics，Chinese Academy of Sciences，Wuhan 430071）

To study the strength and deformation characteristic of unbound granular materials of high-speed railway，a granular flow model is established with the internal FISH language of three-dimensional particle flow code PFC3D.Meanwhile，themicro parameters of unbound granularmaterials are calibrated with the conventional triaxial test results.Considering the influence of the curvature coefficient and the uniformity coefficient on the grain size distribution，five kinds of different grain composition of unbound granular materials are simulated under three different confining pressures.The results show that：There is a predominant factor in the curvature coefficient of unbound granularmaterials.The differences between the effective size，median diameter and constrained size can't be allowed too large，because the strength behaviors of the unbound granular materials with large curvaturecoefficient and uneven coefficient performances are higher than the others，and the deformation behaviors become more and more large.The non-uniformity coefficient is another important factor on the strength and deformation behavior of unbound granular materials.With the larger non-uniformity coefficient and well-graded granular materials won't changing the force chain distribution under the different stress condition，and the extrusion becomes more obvious and the transfer and distribution of force aremore uniform.

Unbound granularmaterial，Curvature coefficient，Non-uniformity coefficient，Stress chain

TU43

：A

10.13544／j.cnki.jeg.2016.06.019

2015－09－06；

2015－12－03.

国家自然科学基金项目（41372314），湘潭大学第七届大学生研究性学习和创新实验计划项目资助.

陈铖（1977－），男，博士，副教授，主要从事岩土材料的本构关系、微细观力学特性与路基填料动力特性等方面的研究.Email：

chencheng401＠sina.com

刘小清（1989－），男，硕士生，主要从事岩土微细观力学特性与路基填料动力特性方面的研究.Email：1295025071＠qq.com