滑坡变形组合预测方法的研究*

孙世国 苏振华 王 杰 郭 珮 董彦飞

（北方工业大学 北京 100144）

滑坡变形组合预测方法的研究*

孙世国 苏振华 王 杰 郭 珮 董彦飞

（北方工业大学 北京 100144）

为了预测边坡变形大小，以便及时采取防治措施，通过取不同的迟滞时间对原始监测数据进行相空间重置获得新的数据序列，再以这些新的数据序列为基础，采用预测残差平方和最小的线性优化方法，将ARMA时间序列法和GM（1，1）灰色理论的预测结果进行组合，对某矿的边坡变形量进行滚动组合预测。对不同方法的预测精度和预测残差的标准差进行了对比分析，结果对比表明，组合预测较单项预测方法残差标准差明显减小，且相空间重置后的组合预测结果提高了直接预测的平均预测精度，这为边坡变形趋势的预测与防灾预警提供了可靠的方法。

边坡变形 滚动组合预测 相空间重置 迟滞时间

0 引 言

做好边坡稳定性的评价与安全控制对于露天矿的安全生产意义重大（张丽等，2004；唐廷宇等，2008；杨天鸿等，2011），及时采取边坡加固措施避免滑坡，可以减少经济损失，提高矿山生产的安全性。这就需要对边坡变形进行预测。

有研究（杨志法等，2004）对滑坡预测预报的方法进行了统计分析，从方法论的角度分为3类：以内因分析为主的方法、以外因分析为主的方法和以监测为主的方法。以内因为主的预测预报研究众多但工作量大且成功率并不高，对内因的分析应是作为滑坡预测预报的前期调研准备工作。在内因分析的基础上，日后滑坡预测预报的方法应以“由天预报地”为主的外因分析方法结合单点滑坡的监测预报方法。

对于单点监测方法，设有原始序列：｛xt，t＝1，为基于前n项实测值的预测值，l为预测步长。出于精度的考虑，计算预测值的时候常取步长为l＝1（孙世国等，2011），这样较短的预测步长往往会导致防灾准备时间与空间的不足，不能减轻灾害损失、及时避险。边坡变形预测研究的方法分为两大类，由于数值模拟常用于稳定性分析（吴韩等，2015），一类是通过数值模拟计算与监测数据对比分析（赵志峰等，2007）；另一类是根据监测资料建立数学模型进行分析与预测。第二类的数学建模方法众多，如斋藤法（苗胜军等，2007）、灰色理论模型（姜刚等，2011；肖云等，2012；王冬等，2013）、ARMA时间序列预测（缪海波等，2009）、BP神经网络方法等。每种独立预测模型针对同一个监测点的预测结果不尽相同，预测精度差别很大。若加大预测步长，单项预测方法的预测精度无法得到保证，故在进行边坡变形趋势预测时应综合考虑多种预测方法，以寻求最佳的预测结果，从而提高预测精度、降低预测风险。

本文采用误差平方和最小的最优的线性滚动组合预测的方法，结合相空间重置的理论，对某矿910、940、964监测点的水平位移进行预测，并对预测结果进行分析。

1 滚动组合预测模型的建立

1.1 数据预处理

为提高组合预测的精度，首先要保证各独立预测方法的精度，依据灰色预测模型需对原始监测数列｛xt，t＝1，2，…，n｝进行级比平滑检验。

称σt为xt的级比：

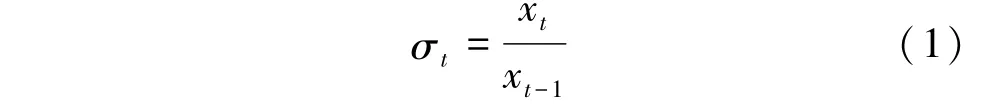
若序列不够光滑平稳，需要对数据进行转换，一般是通过变量替换的方法实现。通常采取对数变换：

或者平方根变换：

当实际处理数据时，视具体情况而定。

1.2 组合模型

针对原始监测数列xt，（t＝1，2，…，n），t时刻的实测值xt对应的共m种独立预测方法的预测序列为xti，（i＝1，2，…m），则xti表示t时刻实测值对应的第i中预测方法的预测结果。第i种独立预测方法t时刻的预测残差为：

假设p1、p2、…pm分别为赋予m种单项预测方法的权重，当权重满足如下关系时：

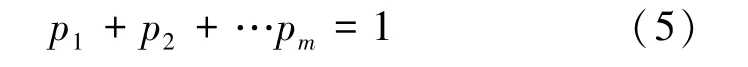
满足无偏性。

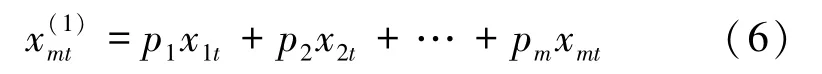
J表示组合预测残差的平方和：

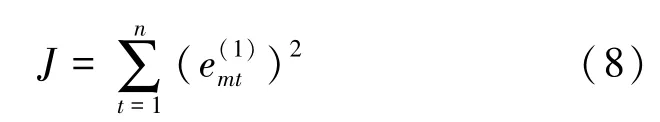
以此建立下列最优化问题，求解权重，计算综合

权重：

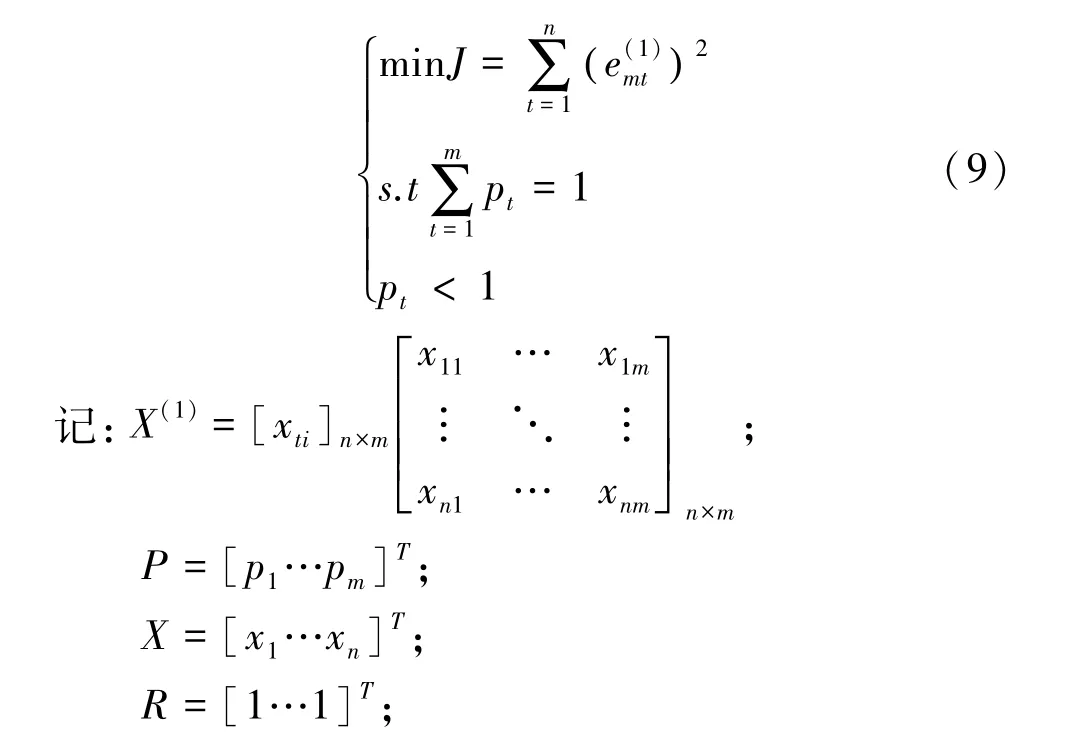
E是单位矩阵；

将式（9）转化为：

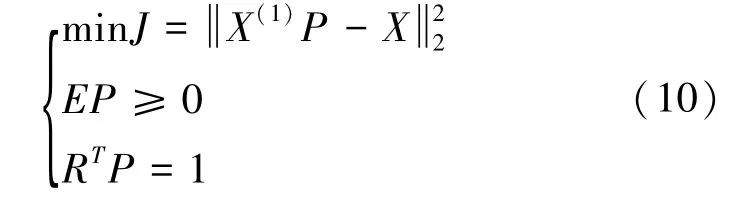
将上述优化问题通过调用MATLAB函数lsqlin（X（1），X，E，0，RT，1）来求解权重向量。将权重向量代入：

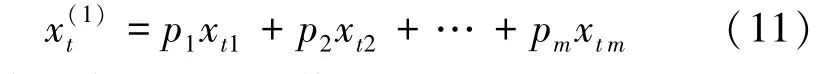
计算组合模型预测值。

1.3 滚动建模的方法

若原始监测数列xt，（t＝1，2，…，n）全部参与建模，时间较久远的数据趋势已经不符合于近期监测数据的变形趋势。

假设xt有拓扑空间：

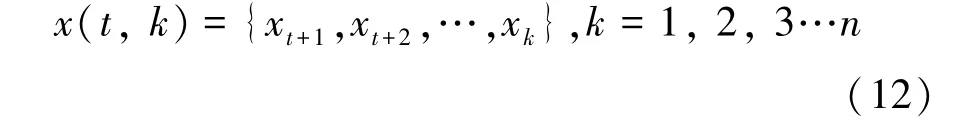
称：

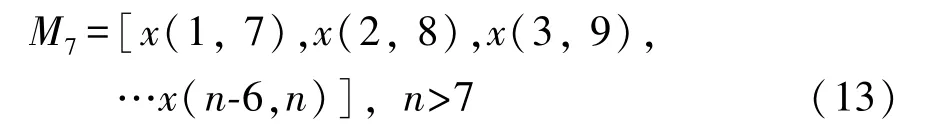
为7维滚动子序列，可满足本文选用的时间序列法和灰色预测对建模序列维数的要求。利用M7这样的滚动子序列，分别求出各独立预测模型与组合预测模型的预测值，叫做滚动建模预测。滚动建模保证了数据的时效性，能提高预测的精确度。

对t时刻的监测点xt，有7维滚动组合预测值x（1）mt，则称：

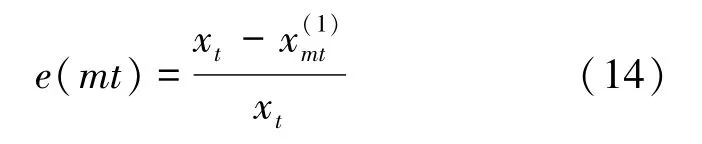
为滚动相对残差。

称：

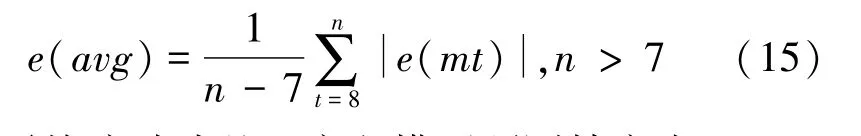
为平均滚动残差。定义模型预测精度为：

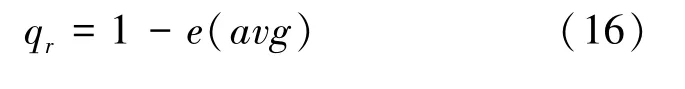
2 相空间重置的方法

影响边坡稳定的因素众多，它们之间的关系也错综复杂，基于该特点，边坡失稳便是一个工程混沌问题。分形（Fractal）是混沌的基本现象之一，指的是整体和局部根据特定的相似方式的一个集合。分形的一个最重要的特征是“自相似性”。“自相似性”的内在含义是每个局部都是整体的一个特例或者缩影，任意的局部特征以一定比例放大后将和整体相似，即任意小的局部都含有整体的信息和缩影。在预测中的体现为预测模型的“尺度”问题。这为预测加大预测步长l提供了理论基础。

相空间重置就是解决分形“尺度”问题的有效手段（周创兵等，2000；王海燕等，2003）。混沌学说明，在一个系统中长期演变的每一个时间序列，都包含着变量的系列演变信息。将相空间容量为n的一维时间序列，经过重置拓展成为d维，则对于重置后的相空间，每一维中的数据都是对原数据自相似性的提取。

原始监测序列｛xt，t＝1，2，…，n｝是一个一维的时间序列，对这n个数值通过取不同的迟滞时间τ，达到建立多维空间的目的（表1），将原始监测时间序列拓展成d维的相空间分布。这里的τ＝kΔt，k＝1，2，3…；Δt为原始序列的监测时间间隔。

表1 相空间重置Table1 Phase-spacereconstruction

相空间重置后，对于每一个相点X（ti）都有d个分量。这样对于每个相点单独进行一步预测，便可实现对整个原始序列迟滞时间为τ的预测。每一步预测都采取多种独立预测模型进行预测，然后以组合模型进行加权得到组合预测值。

边坡变形序列组合预测流程图（图1）。

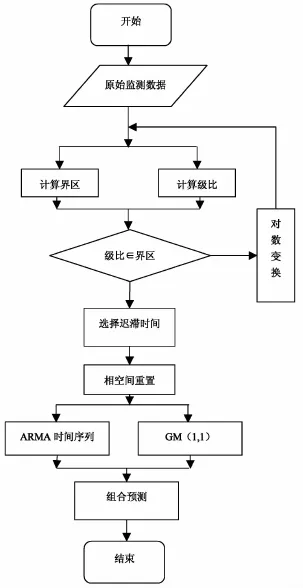
图1 边坡变形组合预测流程图Fig.1 Flowdiagramofslopedeformationcompositiveprediction

3 实例预测与分析

以某矿910、940、964监测点水平位移为例，监测点均位于采场北帮、东帮边坡工作平台，便于边坡变形监测与设备保护。采用灰色滚动预测模型和ARMA时间序列预测模型及其组合模型进行相空间重置变形预测。原始监测点变形观测时间间隔为1周，即t＝1，从2013年8月19日～2014年9月6日，共有55个观测数据，即相空间容量n＝55。

3.1 计算界区和计算级比

将n＝55代入界区计算式得：（0.9649，1.0364）。

将910、940、964原始检测序列代入式（1）计算各监测点级比序列。

910级比序列：

｛2.3096，1.6433…1.0190，1.0118，1.0031，1.0010，1.0028，1.0028，1.0131｝；

940级比序列：

｛1.5547，1.6155…1.0347，1.0326，1.0291，1.0281，1.0253，1.0252，1.0252｝；

964级比序列：

｛2.0078，1.3607…1.0447，1.0499，1.0442，1.0392，1.0373，1.0352，1.0337｝。

3.2 序列光滑性检验及修正

由各序列级比可知，前几项都不在界区，因此前几项不适用建模，另外从建模的时效性出发，建模时往往只选择最新的几个数据，因此前几项往往不参与建模。910和940满足条件，但是964号监测点从第38项开始位于界区以外；而第38项的邻域范围内正是建模序列的关键区域，因此需要对964号监测点的监测数据进行修正。这里我们采用对数变换。

修正后的964级比序列：

｛2.3672，1.6461…1.0269，1.0264，1.0259，1.0255，1.0250，1.0245，1.0241，1.0236｝。

从上述级比序列可以看出：除了前4项，均能满足界区条件，可以进行预测。

3.3 相空间重置及预测

以964监测点水平位移、迟滞时间9周为例。

在原始变形序列｛xt，t＝1，2，…，n｝中，取迟滞时间τ＝9Δt＝9周，相空间的相点个数即为9，已知lorenz吸引子的分维D＝2.06，设相空间维数为d，在满足d≥2D＋1的条件下（修春波等，2003），有

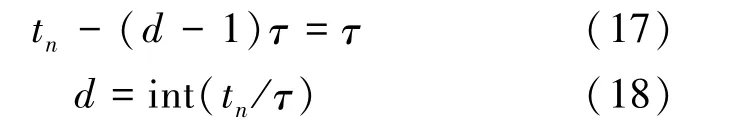
将tn＝n＝55，τ＝9（周），这9个新相点（序列）构成一个相型，带入上式得d＝6，因此新序列的维数等于6，其中前5维用来建模，第6维用来预测检验，即是预测目标。时间序列法需要5维以上的建模序列，灰色空间法需要至少4维的序列，取d≥6，则对于n＝55的序列，最多可以进行τ＝9（周）的预测。

同理，对910、940、964分别取迟滞时间τ＝5、6、7、8、9进行相空间重置及预测。以940监测点数据为基础、迟滞时间9周为例，相空间重置及其预测结果（表2，表3）；910、940、964监测点，采用不同的迟滞时间得到的组合预测结果（表2～表4）。不同监测点的迟滞时间为9周的预测值与实测值对比图（图2～图4）；预测残差标准差SD（J）对比（图5）；相空间重置与直接预测平均预测精度对比（图6）。

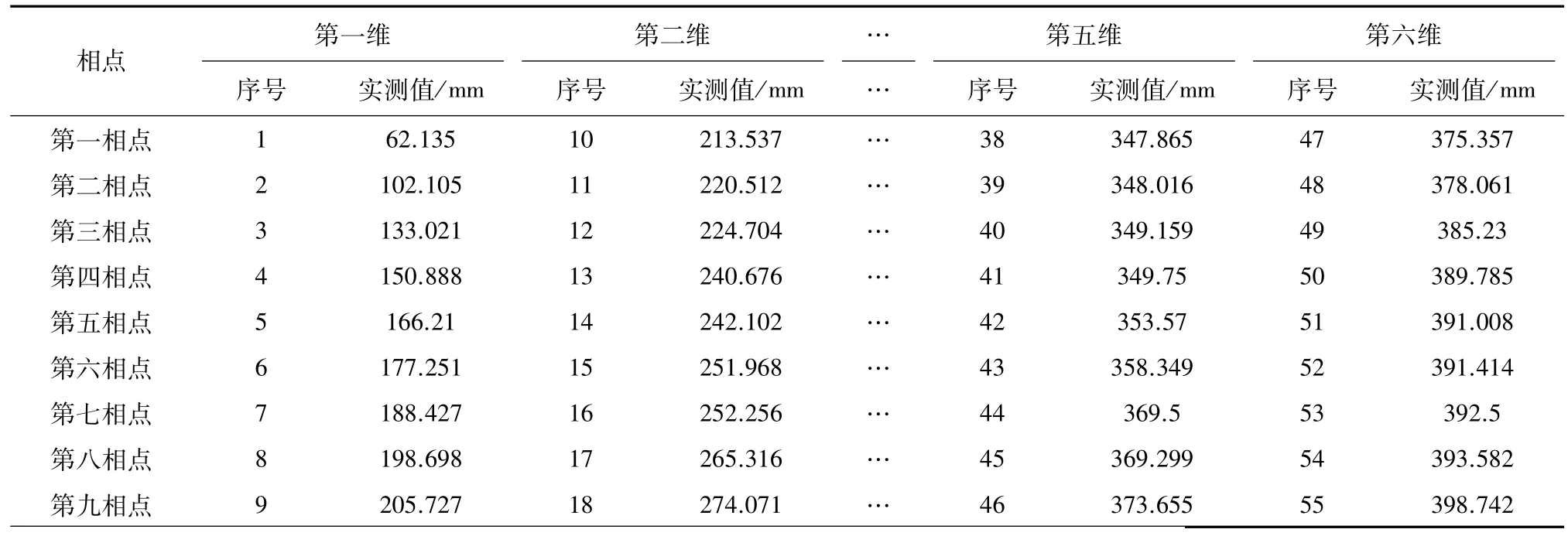
表2 监测点940水平位移的相空间重置（τ＝9）Table2 Phase-spacereconstructionofmonitoringpoint940′shorizontaldisplacement（τ＝9）

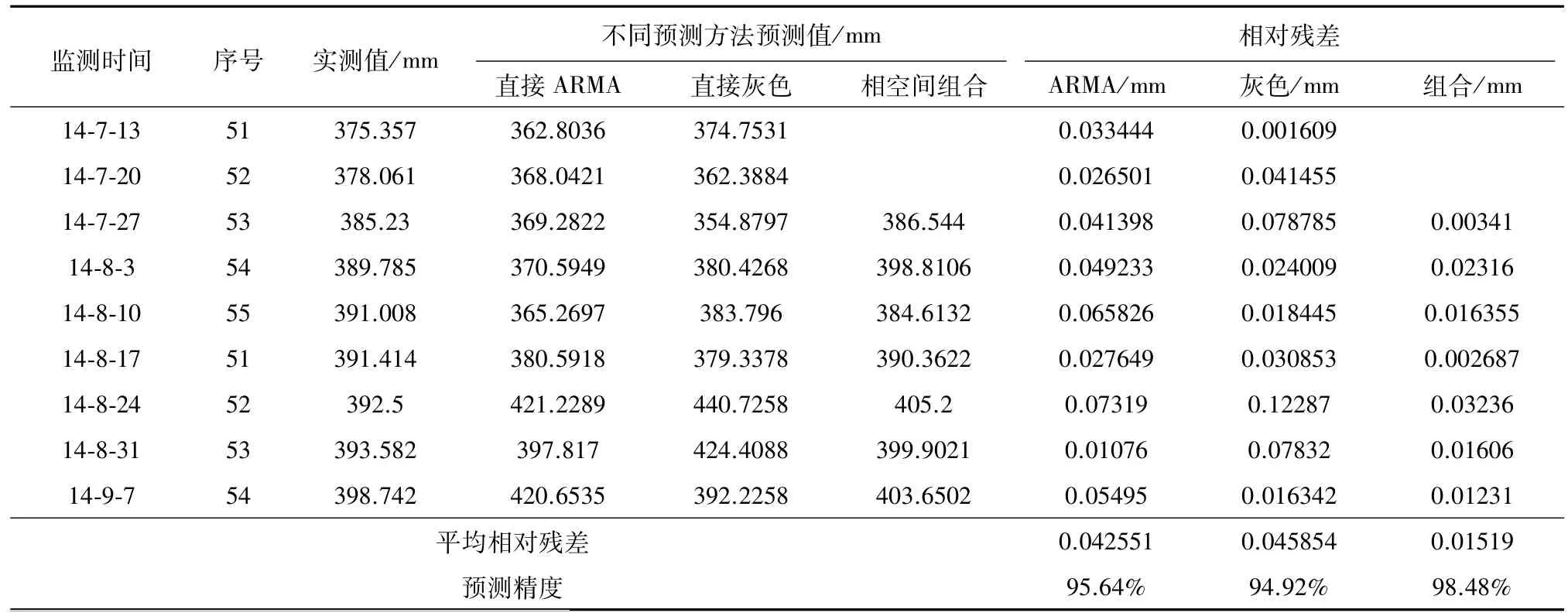
表3 监测点940水平位移的预测值及相对残差（τ＝9）Table3 Phase-spacereconstructionofmonitoringpoint940′shorizontaldisplacement（τ＝9）

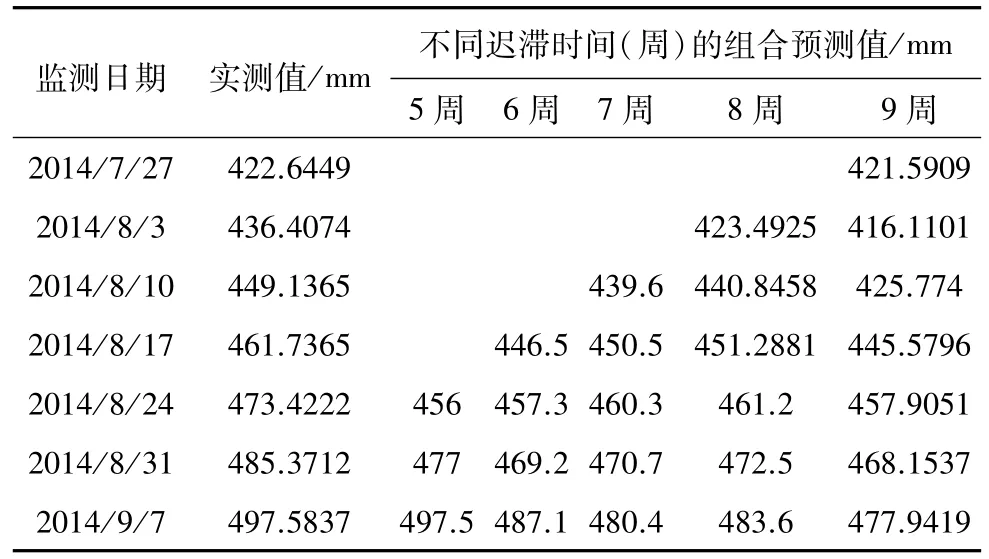
表4 监测点940组合预测值Table4 Compositivepredictionsofmonitoringpoint940

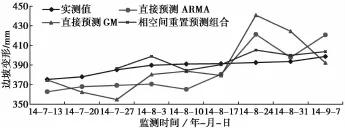
图2 监测点910的预测值与实测值对比（τ＝9）Fig.2 Comparisonofpredictedvaluesandmeasured valuesofmonitoringpoint910（τ＝9）

由图2到图4可以看出，针对不同的监测点，迟滞时间取9周时，与直接的单项方法预测结果相比，相空间重置后的预测值曲线更贴近实测值的曲线，其中图2和图3具有一定的离散性，预测残差标准差越低，则说明预测值离散性低，较稳定。图5显示，迟滞时间为5～9周的残差标准差，除第5周略高于时间序列法，其余数据均显示优于单项预测法，说明该方法能降低预测风险。从图6可以看出，该方法的平均预测精度整体高于单项预测方法。从另一种角度看，随着迟滞时间的增大，预测精度都有降低趋势，但是相空间重置后的预测精度减缓了这一降低趋势。

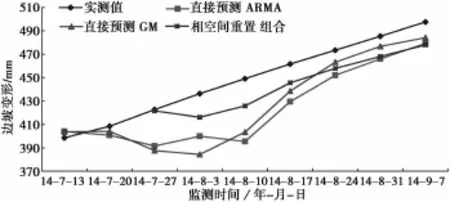
图3 监测点940预测值与实测值对比（τ＝9）Fig.3 Comparisonofpredictedvaluesandmeasured valuesofmonitoringpoint940（τ＝9）

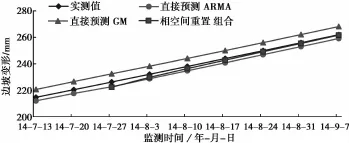
图4 监测点964预测值与实测值对比（τ＝9）Fig.4 Comparisonofpredictedvaluesandmeasured valuesofmonitoringpoint964（τ＝9）

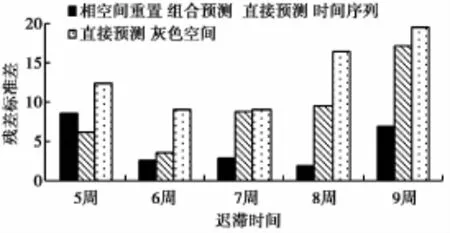
图5 残差标准差对比Fig.5 ComparisonofSTDEVofresidualerror

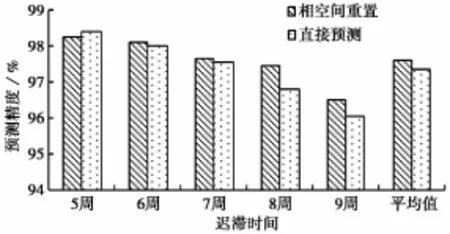
图6 预测精度对比Fig.6 Comparisonofprecisionofprediction

4 结 论

滑坡预测精度决定了预测的准确性，如果未能成功预测滑坡，则会造成巨大的经济损失和社会影响，因此预测精确度非常重要。

与单项预测方法相比，本文通过基于相空间重置的组合预测法提高了较长预测步长的预测精度，预测结果更加安全可靠。若结合合理的监测手段，对于存在失稳危险的边坡变形趋势预测意义重大，可以为安全防控提供科学依据。

JiangG，KangYX，YangZQ，etal.2011.Applicationofgraymodelto landslidedeformationforecastinminingareas［J］.CoalGeology＆Exploration，39（3）：49～51.

LiaoHB，YinKL，ChaiB，etal.2009.Deformationpredictionof landslidebasedontheanalysisofnon-stationarytimeseries［J］. GeologicalScienceandTechnologyInformation，28（4）：107～111. MiaoSJ，CaiMF，LaiXP，etal.2007.Studyondeformationprediction ofimprovedsaito'smethodbasedonVerhulstmodel［J］.China MiningMagazine，16（4）：46～50.

SunSG，YangH.2011.Controltechnologiesoftypicaldumpslope stability［M］.Beijing：PressofMetallurgyIndustry：53～73.

TangTY，ChenFM.2008.Impactingthemainfactorontheopen-mining slopestabilityandprotectionmeasures［J］.MiningEngineering，6（2）：14～15.

WangHY，ShengZH，ZhangJ.2003.Phasespacereconstructionof complexsystemsbasedonmultivariatetimeseries［J］.Journalof SoutheastUniversity，33（1）：115～118.

WangD，HuangX，WangMD，etal.2013.ApplicationofGM（2，1）to predictionoflandslidedeformation［J］.Hydrogeology＆Engineering Geology，40（3）：121～125.

WuH，JianWX，XiaoD，etal.2015.Numericalmodelingmethodfor slopestabilityundervariabledistributionofstrengthparameters［J］. JournalofEngineeringGeology，23（1）：135～139.

XiuCB，LiuXD，ZhangYH.2003.Selectionofembeddingdimension anddelaytimeinthephasespacereconstruction［J］.Transactionsof BeijingInstituteofTechnology，23（2）：219～224.

XiaoY，LiXF.2012.Forecastforlandslidebasedonoptimumgrey model［J］.JournalofWuhanInstituteofTechnology，34（1）：31～35.

YangZF，ChenJ.2004.Thoughtsonthepredictionorforecastof landslides［J］.JournalofEngineeringGeology，12（2）：118～123.

YangTH，ZhangFC，YuQL，etal.2011.Researchsituationofopen-pitmininghighandsteepslopestabilityanditsdevelopingtrend［J］. RockandSoilMechanics，32（5）：1437～1451，1472.

ZhouCB，ChenYF.2000.Applicationofphasespacereconstructionin slopedisplacementforecasting［J］.RockandSoilMechanics，21（3）：205～208.

ZhangL，HuangY，RenL，etal.2004.InquiryintotheInfluencingfactors andanalyticalmethodsofslopestability［J］.YunnanWaterPower，23（4）：22～26.

ZhaoZF，XuWY.2007.Rockslopestabilityanalysisbasedon deformationmonitoringandnumericalsimulation［J］.Journalof HohaiUniversity（NaturalSciences），35（4）：398～403.

姜刚，康艳霞，杨志强，等.2011.灰色理论模型在矿区滑坡变形预测中的应用［J］.煤田地质与勘探，39（3）：49～51.

缪海波，殷坤龙，柴波，等.2009.基于非平稳时间序列分析的滑坡变形预测［J］.地质科技情报，28（4）：107～111.

苗胜军，蔡美峰，来兴平，等.2007.基于Verhulst模型改进的“斋藤法”变形趋势预报研究［J］.中国矿业，16（4）：46～50.

孙世国，杨宏.2011.典型排土场边坡稳定性控制技术［M］.北京：冶金工业出版社：53～73.

唐廷宇，陈福民.2008.影响露天矿边坡稳定的主要因素及防范措施［J］.矿业工程，6（2）：14～15.

王海燕，盛昭瀚，张进.2003.多变量时间序列复杂系统的相空间重构［J］.东南大学学报，33（1）：115～118.

王冬，黄鑫，王明东，等.2013.灰色GM（2，1）模型在滑坡变形预测中的应用［J］.水文地质工程地质，40（3）：121～125.

吴韩，简文星，肖迪，等.2015.岩土体力学参数空间分布下的滑坡稳定性数值计算方法［J］.工程地质学报，23（1）：135～139.

修春波，刘向东，张宇河.2003.相空间重构延迟时间与嵌入维数的选择［J］.北京理工大学学报，23（2）：219～224.

肖云，李先福.2012.基于优化的灰色GM模型的滑坡预测［J］.武汉工程大学学报，34（1）：31～35.

杨志法，陈剑.2004.关于滑坡预测预报方法的思考［J］.工程地质学报，12（2）：118～123.

杨天鸿，张锋春，于庆磊，等.2011.露天矿高陡边坡稳定性研究现状及发展趋势［J］.岩土力学，32（5）：1437～1451，1472.

周创兵，陈益峰.2000.基于相空间重构的边坡位移预测［J］.岩土力学，21（3）：205～208.

张丽，黄英，任磊，等.2004.边坡稳定影响因素及稳定分析方法探讨［J］.云南水力发电，23（4）：22～26.

赵志峰，徐卫亚.2007.基于监测与数值模拟的岩质边坡稳定性分析［J］.河海大学学报，35（4）：398～403.

RESEARCH ON THE SYNTHETICAL PREDICTION METHOD OF LANDSLIP DEFORMATION

SUN Shiguo SU Zhenhua WANG Jie GUO Pei DONG Yanfei
（North China University of Technology，Beijing 100144）

For predicting amine's slope deformation so as to adopt timely safety measures，this paper proposes a new dynamic synthetical predictionmethod.With the help of phase-space reconstruction by substituting different lag time，a new data series from the originalmonitoring data was get for this method.It took the linear optimization method，which on the condition of theminimum sum of squares of prediction residue error，to calculate theweights of differentmethods'predictions，such as ARMA time series and GM（1，1）grey theory.The comparison of the results indicates that，the standard deviation of the synthetical prediction is reduced obviously compared with independent approaches；predictions after the Phase-space reconstruction can improve the average precision.And this provides a reliablemethod for the forecast and precaution for each kind of landslide.

Slope deformation，Dynamic synthetical prediction，Phase-space reconstruction，Delay time

P642.22

：A

10.13544／j.cnki.jeg.2016.06.001

2015－08－04；

2015－12－22.

国家自然科学基金（41172250），国家十二五科技支撑项目（2012BAK09B06），北京市创新团队提升计划项目（IDHT20140501），北京市科研基地建设－科研创新平台、科研专项－冲击地压微震监测与预警体系的构建（XN083），新型锚杆加固技术现场试验研究及研究生能力实训（XN107）资助.

孙世国（1967－），男，博士后，教授，博士生导师，主要从事矿山安全生产方面的研究.Email：ssg918＠163.com