泥石流流变参数敏感性分析*
徐继维张茂省于国强
(①长安大学地质工程与测绘学院 西安 710054)
(②国土资源部黄土地质灾害重点实验室 西安 710054)
(③中国地质调查局西安地质调查中心 西安 710054)
泥石流流变参数敏感性分析*
徐继维①②张茂省②③于国强②③
(①长安大学地质工程与测绘学院 西安 710054)
(②国土资源部黄土地质灾害重点实验室 西安 710054)
(③中国地质调查局西安地质调查中心 西安 710054)
合理的流变参数选取对准确刻画泥石流、高速远程滑坡运动过程和动力行为至关重要。本研究基于三维连续介质动态数值模型,构建Voellmy流变模型,结合方差分析方法,比较了不同流变参数对泥石流运动行为的影响程度。结果表明:动力底摩擦角和湍流系数均会对泥石流与高速远程滑坡的动力特征产生一定的影响,但影响程度各异。较大的动力底摩擦角会产生更大、更快的能量耗散过程,使得运动过程整体滞后;较高的湍流系数增加了流体层之间的动量交换强度,具有较大的与周围界质混合的能力,对周围介质的卷吸作用增大。物源区体积(湍流系数)在一定程度上仅影响泥石流运动速度,对致灾范围和规模影响作用不大。沟道下垫面情况、颗粒物组成、孔隙水压力(底摩擦角)与灾害体流速、移动距离和堆积区体积、面积关系很密切,在很大程度上影响泥石流、滑坡强度,致灾范围和规模。研究成果以期为流变参数选取提供很好的借鉴方法,也为地质灾害防治提供一定的技术参考。
泥石流 流变参数 敏感性 数值模型
0 引 言
数值模拟技术是处理动力学难题的一种方法。数值实验中,通过调试参数和边界条件,可以再现真实的力学过程。虽然还不能完全替代物理实验,但可以和物理实验相互结合而被广泛推广,目前数值模拟技术已经成为复杂力学机制研究中重要的技术手段方法(Chen et al.,2000,2003,2006)。
泥石流、滑坡致灾范围及动力参数预测模型方面,经历了20多年的历史。随着计算机运算速度的迅速提高和微分方程求解新算法的提出以及对动力过程深入的了解,其数值模拟研究得到了迅速发展,已经成为泥石流、滑坡动力过程以及机理研究的一个重要内容,并取得了一系列研究成果(Erlichson,1991;Fannin et al.,2001;Chen et al.,2006)。根据目前研究成果,可以将预测模型大体分为3大种类:经验法、物理尺度模型法和动态模型法,其具体方法体系分类(图1)。

图1 预测模型方法体系Fig.1 Themethods of prediction model for hazard area and the kinematic parameters
经验法是参照实际滑坡、泥石流数据并且依照合适的滑坡、泥石流分类方法而发展建立起来的,已有多处成功案例。总的来说,经验法提供了一种相对单一且实用的工具进行运动距离的分析,但并未考虑物体流变特性和动力参数的机理信息,而且此类方法需要依赖于足够的野外观测数据,来预测经验关系,因此不能加以扩展推广,不能用于预测其他地区案例的移动距离。物理尺度模型法是对开展泥石流、滑坡试验研究,可以在野外和室内展开。全球范围内仅在日本火烧岳和云南蒋家沟对滑坡、泥石流进行系统地野外观测。但由于野外进行直接观测十分困难,解释野外沉积物质时的不确定性也会限制野外调查的有效性,而未能得以推广;该方法另外一个方向是在室内展开物理模型试验。然而,对于大规模灾害评价,由于模型尺度效应或物理相似性不确定性的原因,试验结果应用于野外情况时受到限制。动态模型法中的质量集中模型是基于能量准则提出改进的“雪橇”模型,假设在滑坡和泥石流的运动过程中,所有的能量损失都是通过摩擦消散的,能够反映出固有的内摩擦角和孔隙水压力的组成的综合效应,由于其简洁而具有一定的优势(Erlichson,1991;Fannin et al.,2001;Crosta et al.,2004;Chen et al.,2006)。但该模型将物体的形心和重心合为一点,因此并不能够考虑到失稳形态的复杂模式和滑坡物质的内部变形,同时它也不能识别基底高程和下坡条件,并且不能考虑到动力要素的改变和流体前端运动(Chen et al.,2000,2003,2006)。独立单元法是颗粒状集合体力学数值技术,如采用二维颗粒流程序PARTI-2D和UDEC对颗粒流问题进行数值模拟,已经成功用于分析香港滑坡案例。这些方法在过度关注了粒子之间的相互作用,对于泥石流、滑坡的研究而言,更多的是需要关注其宏观行为,诸如传播物质运动和沉积速度分布、灾害区和不稳定自由表面流动特征等,因此独立单元法具有一定的片面性。
连续介质模型在以上模型基础上发展而来的,能够精细刻画泥石流、滑坡动力过程,具有一定的普遍性(Erlichson,1991;Fannin et al.,2001;Crosta et al.,2004;Chen et al.,2006)。流变模型通常选取摩擦模型、Voellmy模型和Bingham模型(Hungr et al.,1984;Hungr,1990;Jakob,2005)来描述泥石流和高速远程滑坡的运动机理。流变模型确定后,选择合理的流变参数对模拟的准确性至关重要。一些流变参数往往没有明确的物理含义,多为经验参数,虽然在许多案例中多有成功的应用,但由于其参数物理意义以及其对模拟的结果有多大程度的影响尚不明确,在实际流变参数选择过程中,往往难以选择。鉴于此,本研究采用有限元求解方法,应用三维连续介质动态数值模型方法,选取Voellmy流变模型,对不同流变参数情况下的泥石流或高速远程滑坡动力过程,流变参数对运动行为的敏感性展开了研究,以期为流变参数选取提供很好的借鉴,也为地质灾害防治提供一定的技术参考。
1 试验材料与方法
1.1 流变模型选用
如前所述,连续介质模型能够很好地刻画泥石流和高速远程滑坡的运动及变形特性。其连续介质模型的理论、数学原理、基底侵蚀机制和质量守恒、受力分析和动量守恒的数学公式详见文献(Crosta et al.,2004;Chen et al.,2006)。泥石流和高速的流变特性是指流体变形所受剪应力与剪切率的关系(Chen et al.,2006)。通常选取摩擦模型、Voellmy模型和Bingham模型(Hungr et al.,1984;Hungr,1990;Jakob,2005)描述这种流体关系。根据文献记载(Fannin et al.,2001;Crosta et al.,2004;Chen et al.,2006),Bingham模型主要适合于固体物质以土为主的黏性泥石流,属于均匀细颗粒物质占主体的泥石流流体;而Voellmy模型是在摩擦模型(Friction model)的基础上加入了经验参数湍流(紊

式(1)中,μ为动力摩擦系数,μ=(1-γu)tanδ,γu为孔隙水压力比率;ξ为湍流系数,代表了流体流动过程中湍流的影响,许多泥石流在传递过程中都具备了湍流的性质;湍流是不稳定的结果。湍流运动在统计意义上可以归纳为平均数量部分,如将速度场和压力场分为平均部分和波动部分。当模型中未考虑湍流项(ξ→∞)时,Voellmy模型则简化为摩擦模型(Chen et al.,2006)。
1.2 实验设计与模型几何结构
本研究构建限制坡地形进行数值模拟(图2),限制坡用以控制物质侧向运动。模型几何结构设计成一倾斜的40°坡面、5°线性过渡区和一个水平面,物源质量中心投影中心与水平面的直角坐标系原点重合(图2)。所有模拟试验均是在斜坡上部同一位置、相同数量的物源开始。流)系数ξ,两者经常应用于颗粒流和大块岩石崩塌、流动。本研究选用Voellmy流变模型开展数值模拟。
Voellmy模型主要考虑了流体的湍流和摩擦两种行为,如下式:

图2 数值模型示意图Fig.2 Set-up of the numericalmodel
整个斜坡在y轴方向宽度为8m(y:-4—+4m),在x轴方向坡面长11m(x:-2—+9m),过渡区长2m(x:+9—+11m),水平区域长9m(x:+11—+20m)。限制坡凹陷部分宽4m,最深处达0.25m。物源区为一球冠,高度为0.25m,投影半径为2m。该物源区球冠体积计算为1.58m3。材料在坡面上释放,延过渡区域运动到水平面上。
为了讨论流变参数对模拟结果的影响,本研究选用上述40°限制坡面进行模拟。选用Voellmy流变模型,同时考虑动力底摩擦角δ和湍流系数ξ对结果的影响。其中动力底摩擦角δ包括6种角度(6°~16°、Δδ=2°为一间隔),湍流系数ξ包括9类工况(500~1300m·s-2、Δξ=100m·s-2为一间隔),共模拟54种工况。
2 结果与讨论
2.1 不同流变参数下运动过程分析
根据以上实验设计,本研究对这54种工况进行了数值模拟研究,选取了泥石流最大速度(前端速度)、最远移动距离以及堆积区面积、体积作为参考指标。同时采用surfer 8.0绘制各种工况条件下,各指标的三维表面图(图3),该图呈现了在不同动力底摩擦角δ和不同湍流系数ξ下,4个指标的对比情况。
从图3可以看出,在各个工况条件下泥石流最大速度(前端速度)的变化趋势同泥石流移动距离、堆积区面积、体积变化趋势基本一致,但变化趋势更为线性,三维表面近似平面。在湍流系数ξ一定的情况下,随着动力底摩擦角δ的逐渐增加,最大速度(前端速度)成线性减小趋势,在不同的湍流系数ξ下,其下降趋势与程度基本一致;在动力底摩擦角δ一定的情况下,随湍流系数ξ的逐渐增加,最大速度(前端速度)基本成线性逐渐增加,在不同的动力底摩擦角δ下,其增加趋势和幅度基本一致。
从图3b~图3d同样也可以看出与最大速度(前端速度)相类似的情况,在各个工况条件下泥石流移动距离、泥石流堆积区面积、体积变化趋势一致,三维表面成曲面形状。在湍流系数ξ一定的情况下,随着动力底摩擦角δ的逐渐增加,泥石流移动距离、堆积区面积和体积成下凹型减小趋势,在不同的湍流系数ξ下,其下降趋势一致,但下降程度随着湍流系数ξ的增加稍有增加;在动力底摩擦角δ一定的情况下,随湍流系数ξ的逐渐增加,泥石流移动距离、堆积区面积和体积基本成线性逐渐增加,增加幅度不大,随动力底摩擦角δ的逐渐增加,其增加幅度逐渐减小。

图3 各指标三维表面图Fig.3 Three-dimensional surfacemap of each indexa.最大速度(前端速度);b.移动距离;c.堆积区面积;d.堆积区体积
图4 、图5分别展示了在不同动力底摩擦角和湍流系数下泥石流运动的模拟结果,反映出泥石流在运动过程中,在水平面的运动物质深度和轮廓情况。虚线代表泥石流运动轮廓线,间隔0.5s,云图代表泥石流堆积深度。

图4 不同动力底摩擦角下泥石流运动模拟结果Fig.4 Projection of debris profiles on horizontal plane under different dynamic basal friction angles a.动力底摩擦角δ=6°,湍流系数ξ=500m·s-2;b.动力底摩擦角δ=16°,湍流系数ξ=500m·s-2
图4 呈现了在湍流系数ξ为500m·s-2,动力底摩擦角δ分别为6°和16°下的运动情况。可以看出两种动力学参数下,表现出相似的动力过程。参考各指标三维表面图3和图4所呈现的实际运动过程可以看出,底摩擦角使运动过程产生差异,底摩擦角较大条件下,运动滞后,堆积区物质部分还停留在过渡区范围内,运动过程持续时间较长,速度慢。底摩擦角影响泥石流的规模和堆积位置,较高的摩擦角会产生更快、更大的能量消耗,运动规模也相对较小(Hungr et al.,1984;Hungr,1990;Jakob,2005),同时也表明在有水存在的条件下,往往会产生大规模的泥石流、滑坡灾害。
图5呈现了在动力底摩擦角δ为12°,湍流系数ξ分别为500m·s-2和1300m·s-2下的运动情况。可以看出,在不同的湍流系数条件下,动力过程相似。参考各指标三维表面图3和图5所呈现的实际运动过程可以看出,不同的湍流系数可使运动过程产生差异。由于较大的湍流项,增加了流体层之间的动量交换强度,具有较大的与周围界质混合的能力,对周围介质的卷吸作用增大,因此泥石流运动速度和堆积区面积、体积明显增加(Hungr et al.,1984;Hungr,1990;Jakob,2005)。同时,湍流系数也影响着最终堆积位置和运动规模,较大的湍流系数使得泥石流运动距离增大,致灾范围和规模(堆积区面积和体积)增加。

图5 不同湍流系数下泥石流运动模拟结果Fig.5 Projection of debris profiles on horizontal planeunder different turbulence coefficients a.动力底摩擦角δ=12°,湍流系数ξ=500m·s-2;b.动力底摩擦角δ=12°,湍流系数ξ=1300m·s-2
综合以上分析可知,动力底摩擦角δ和湍流系数ξ均可在一定程度上影响着泥石流运动的位置、强度和规模。通过改变阻力项或湍流项,可以改变底部阻力或流体层之间的动量交换强度,从而影响着泥石流的运动速度、运动距离以及规模(堆积区面积和体积)。为了进一步讨论试验范围内,动力底摩擦角δ和湍流系数ξ对泥石流强度(运动速度)和规模有何程度的影响,本次研究对不同动力底摩擦角和湍流系数条件下的泥石流流速、运动距离、堆积区体积和面积进行单因素方差分析和双因素方差分析。
2.2 泥石流强度和规模的单因素方差分析
在一定的坡型和坡度条件下,存在动力底摩擦角δ和湍流系数ξ两个相对独立因素。在此,本研究两个参数对泥石流的敏感性进行进一步分析。首先对不同底摩擦角δ和湍流系数ξ下的泥石流流速和堆积区体积、面积开展单因素方差分析。
采用SPSS22软件,对不同动力底摩擦角δ下的泥石流最大流速、移动距离、堆积区面积和体积分别进行单因素方差分析(表1)。可以看出,最大速度(前端速度)、移动距离、堆积区体积和堆积区面积的F检验值均大于1,组内方差小于组间方差,表明分组造成的差异很大,且显著性水平sig.值为0.00,即认为不同的动力底摩擦角δ之间,泥石流最大流速、移动距离、泥石流规模(堆积区体积和面积)的均值是有差异的。

表1 不同动力底摩擦角δ条件下单因素方差分析结果Table 1 One-way ANOVA results under different dynamic basal friction angle
继续对不同湍流系数ξ下的泥石流最大速度(前端速度)、移动距离、堆积区体积和堆积区面积进行方差分析,其方差分析结果(表2)。可以看出,最大流速的F检验值大于1,分组造成的差异较大。且显著性水平sig.值为0.00,即认为不同湍流系数ξ条件下的泥石流最大流速均值存在差异,说明湍流系数对泥石流最大流速影响较大,各个湍流系数下的泥石流最大流速在0.05水平上存在明显差异。相反,泥石流移动距离的F检验值稍稍大于1,堆积区体积和面积的F检验值小于1,这说明组间方差小于组内方差,且观察的显著性水平sig.值均大于0.05,因此可以接受原假设,即认为不同湍流系数ξ条件下的泥石流移动距离、堆积区体积和面积均值不存在明显差异,说明湍流系数对泥石流移动距离、堆积区体积和面积影响较小,各个湍流系数下的泥石移动距离、规模(流堆积区体积和面积)在0.05水平上不存在明显差异。
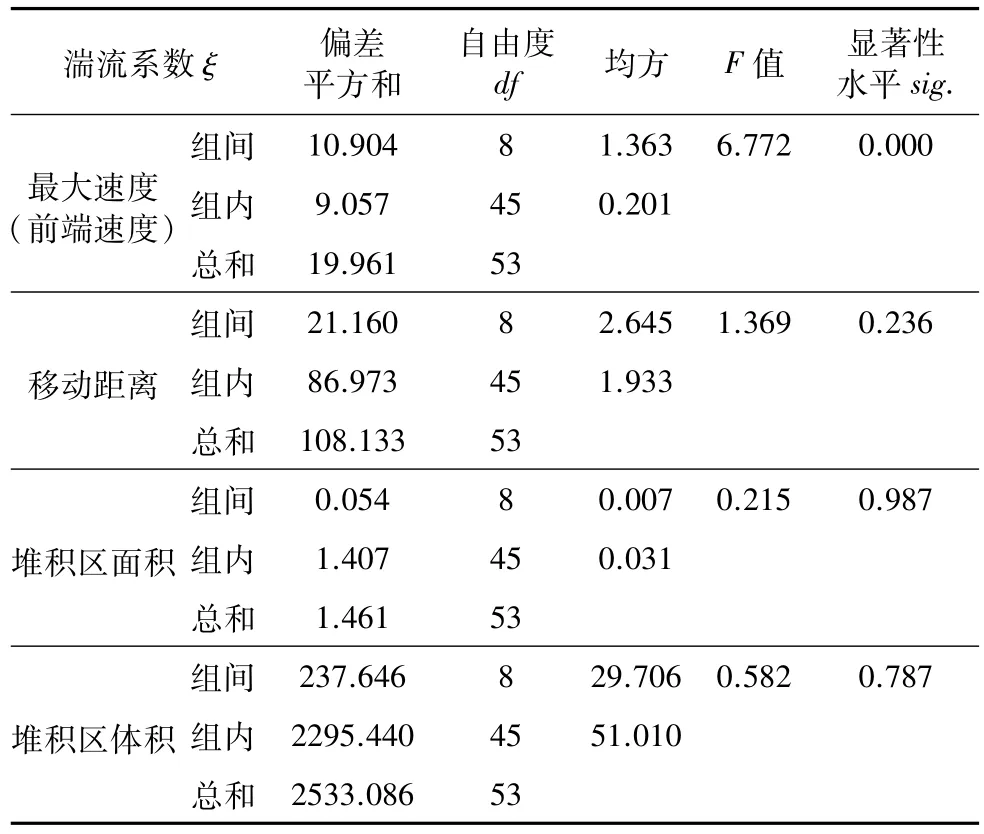
表2 不同湍流系数ξ条件下单因素方差分析结果Table 2 One-way ANOVA results under different turbulence coefficient
2.3 泥石流运动速度二因素方差分析
在上述分析的基础之上,综合考虑动力底摩擦角、湍流系数两者主效应以及两者的交互效应,开展二因素方差分析。
参考各指标三维表面图3和从图6可知,在不同的动力底摩擦角和湍流系数下,最大速度(前端速度)的变化趋势一致,其变化规律已在上节叙述,在此不再赘述。从图中还可以看出,动力底摩擦角和湍流系数的最大速度(前端速度)变化线性变化没有交叉现象,而且几乎是平行的。这说明不论是采用哪个动力底摩擦角,随着湍流系数的增加,最大速度(前端速度)会逐渐增大,概无例外;不论是采用何湍流系数,随动力底摩擦角的增加,最大速度(前端速度)会逐渐减小,也无例外。表明动力底摩擦角和湍流系数对泥石流最大流速的影响是独立的,不存在两者之间的交互效应,只存在主因素效应。
从表3可以看出,动力底摩擦角和湍流系数的F值都大于1,其sig.值都远远小于0.05,说明不同动力底摩擦角和不同湍流系数的泥石流最大流速存在明显差异,这点已经在上节中得以证明。从两者的F值大小还可以看出,动力底摩擦角对最大流速的影响要大于湍流系数的影响。

图6 不同动力底摩擦角和湍流系数下的泥石流最大流速均值图Fig.6 The varation of themaximum velocity of debris flow under different turbulence coefficient and dynamic basal friction angle

表3 无交互效应的最大流速二因素方差分析Table 3 Two-way ANOVA results of themaximum velocity without interaction
综合以上分析可知,不同动力底摩擦角之间,泥石流最大流速、移动距离、泥石流堆积区体积和面积存在明显差异,不同湍流系数下,只有泥石流最大流速存在明显差异。说明动力底摩擦角对泥石流强度(流速、移动距离)和规模(堆积区面积、体积)有较大的影响,而湍流系数仅对泥石流流速有较大影响,对泥石流移动距离和规模影响较小。动力底摩擦角和湍流系数均对泥石流流速有较大影响,动力底摩擦角的作用要强于湍流系数,且并不存在两者之间的交互效应对流速的影响。
根据文献记载(Hungr et al.,1984;Hungr,1990;Jakob,2005)湍流系数与泥石流物源区体积成正比,而动力底摩擦角与沟道下垫面情况、泥石流颗粒物组成和孔隙水压力有关,因此,泥石流物源区体积在一定程度上仅影响泥石流流速,但对泥石流致灾范围和规模影响作用不大;下垫面情况、泥石流颗粒物组成以及基质吸力与泥石流流速、移动距离和堆积区体积、面积关系很密切,可以在很大程度上影响泥石流强度,致灾范围和规模。
3 结 论
本研究采用有限元求解方法,基于三维连续介质模型,构建了数学模型,并且采用Voellmy模型进行数值模拟实践。此外,我们建立了数值实验,评估Voellmy模型中动力底摩擦角和湍流系数对泥石流运动行为、整体动力性能的影响程度。
结果表明,动力底摩擦角和湍流系数均会对泥石流与高速远程滑坡的动力特征产生一定的影响,但影响程度各异。较大的动力底摩擦角通过阻力项的增加,会产生更大、更快的能量耗散过程,使得运动过程整体滞后;如果底面存在水压力作用,有效孔隙水压力会进一步增大,底面等效底摩擦角将显著的降低,会造成更大的远程灾害。较高的湍流系数会使湍流项显著增加,增加了流体层之间的动量交换强度,具有较大的与周围界质混合的能力,对周围介质的卷吸作用增大,使得运动速度和体积增加。
通过方差比较可知,物源区体积(湍流系数)在一定程度上仅影响泥石流运动速度,对致灾范围和规模影响作用不大。沟道下垫面情况、颗粒物组成、孔隙水压力(底摩擦角)与灾害体流速、移动距离和堆积区体积、面积关系很密切,在很大程度上影响泥石流、滑坡强度,致灾范围和规模。研究成果以期为流变参数选取提供很好的借鉴方法,也为地质灾害防治提供一定的技术参考。
Chen H,Lee C F.2000.Numerical simulation of debris flows[J]. Canadian Geotechnical Journal,37(1):146~160.
Chen H,Lee C F.2003.A dynamicmodel for rainfall-induced landslides on natural slopes[J].Geomorphology,51(4):269~288.
Chen H,Dadson S,Chi Y G.2006.Recent rainfall-induced landslides and debris flow in northern Taiwan[J].Geomorphology,77(1—2):112~125.
Crosta G B,Chen H,Lee C F.2004.Replay of the 1987 Val Pola Landslide,Italian Alps[J].Geomorphology,60(1—2):127~146.
Erlichson H.1991.A mass-changemodel for the estimation of debris-flow runout,a second discussion:Conditions for the application of the rocket equation[J].Journal of Geology,99(4):633~634.
Fannin R J,Wise M P.2001.An empirical-statistical model for debris flow travel distance[J].Canadian Geotechnical Journal,38(5):982~994.
Hungr O,Morgan G C,Kellerhals R.1984.Quantitative analysis of debris torrent hazards for design of remedial measures[J].Canadian Geotechnical Journal,21(4):663~677.
Hungr O.1990.A mass-change model for the estimation of debris-flow runout:a discussion[J].Journal of Geology,98(5):792~792.
Jakob M.2005.Debris-flow hazard analysis[M]∥Jakob M,Hungr O. Debris-flow hazards and related phenomena.Berlin:Praxis-Springer:411~443.
ANALYSIS ON SENSITIVITY OF RHEOLOGICAL PARAMETERS TO DEBRIS FLOW
XU Jiwei①②ZHANG Maosheng②③YU Guoqiang②③
(①College of Geological Engineering and Geometry,Chang'an University,Xi'an 710054)
(②Key Laboratory for Geo-hazards in Loess Area,MLR,Xi'an 710054)
(③Xi'an Center of Geological Survey,China Geological Survey,Xi'an 710054)
Reasonable selection of rheological parametersmay play a role in delineating the runout processmobility behavior of debris flow and high speed and long distance landslide.In this study,three-dimensional continuum model simulation method is applied using voellmy model and analysis of variance,to study the dynamic process under different rheological parameters,and to a compare the sensitivity degree of rheological parameters to runout behavior.The results show that dynamic basal friction angle and turbulence coefficient can influence the dynamic characteristics of debris flow and high speed and long distance landslide to a different degree.The higher dynamic basal friction angle will produce bigger and faster energy dissipation process,making the wholemovement processlag;the higher turbulence coefficient increased strength momentum exchange between the fluid layers,with great ability to mix media around,and increased entrainment effect.The basal topography is an important factor influencing the debris transportation and deposition processes.The underlying surface conditions,particles of debris,porewater pressure has a very close connection with velocity,runout distance and deposition area,volume,and can affect the debris intensity and disaster area and scale to a large extent.The proposed suggestions can be estimated conveniently in general geotechnical practices and can provide the scientific basis for regional disaster prevention and reduction and scientific research.
Debris flow,Rheological parameter,Sensitivity,Numericalmodelling
P642.23
:A
10.13544/j.cnki.jeg.2016.06.003
2014-09-05;
2016-06-16.
国家自然科学基金项目(41530640,41302224),陕西省科学技术研究发展计划项目(2014KJXX-20),中国地质调查局地质调查项目(121201011000150022)资助.
徐继维(1987-),男,博士生,主要从事地质灾害、风险评估研究.Email:xujiwei@chd.edu.cn
于国强(1979-),男,博士,从事土壤侵蚀与水土保持及地质灾害等方面的研究.Email:yuguoqiang23@163.com

