基于指数脉冲函数复调制的滤波器组设计
樊新海, 张传清, 邱绵浩, 孙国强
(装甲兵工程学院机械工程系, 北京 100072)
基于指数脉冲函数复调制的滤波器组设计
樊新海, 张传清, 邱绵浩, 孙国强
(装甲兵工程学院机械工程系, 北京 100072)
针对数字信号处理中滤波器组的设计问题,研究了指数脉冲函数的时域、频域特点,通过对指数脉冲函数进行修正,得到了易于应用的时域表达式,给出了一种通过指定各子滤波器的中心频率和带宽,利用复调制手段设计数字滤波器组的方法,并通过实例验证了其有效性和实用性。
信号处理; 数字滤波器组设计; 指数脉冲函数; 复调制
在复杂信号处理中,常把信号分解为特定频带的子带信号,但由于各子带信号所包含信息的重要程度不同,因此对这些子带信号进行深入分析是一种有效的信号处理手段[1]。此时,需要设计滤波器组,并对信号进行滤波,如:通过设计Gammatone滤波器组,在语音信号处理中可以模拟人耳耳蜗基底膜的分频作用[2-3],在振动信号处理中可以有效地提取齿轮系统侧隙诱发的机械振动冲击特征[4]。笔者对指数脉冲函数的时域、频域特点进行研究,通过修正指数脉冲函数得到更加便于应用的时域表达式,进而给出一种利用复调制和冲激响应不变法快速设计数字滤波器组的方法。
1 理论基础
1.1 指数脉冲函数
因果的指数脉冲函数表达式为
f(t)=tne-atu(t),a>0,n∈N,
(1)
式中:u(t)为单位阶跃函数。由于因果信号在t<0时信号取值为0,而本文只研究t>0的情况,因此在后文的因果信号公式中均略去u(t)。
合理选择n和a,可使得f(t)在时域或频域具有良好的集中性。f(t)的傅里叶变换为
(2)
其模为
(3)
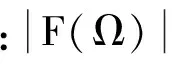
1.2 指数脉冲函数的修正
为了应用方便,采用Fmax对f(t)进行修正,将式(1)改写为
f(t)=an+1tne-at/n!,a>0,n∈N,
(4)
相应地,式(2)、(3)分别变为
(5)
(6)
这样可保证在Ω=0处|F(Ω)|的最大值Fmax=1。
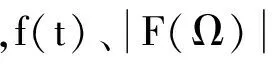
由图1、3可见:f(t)关于峰值点是非对称的,具有先单调快速增加到峰值后又单调缓慢递减的波形特点,与具有一定持续时间和强度的脉冲信号非常相似,故常用于模拟脉冲信号;理论上,f(t)是无限长的,只有当t→∞时,才能使f(t)→0,但当f(t)很小时,就可近似认为f(t)=0;减小n或增大a可以增大f(t)的峰值,缩短达到峰值的时间和脉冲持续时间,提高时域集中性。
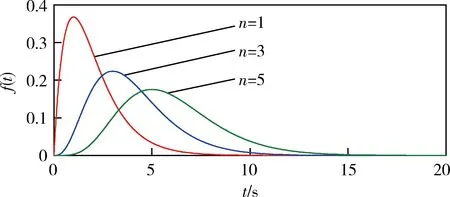
图1 不同n时f(t)的波形(a=1)
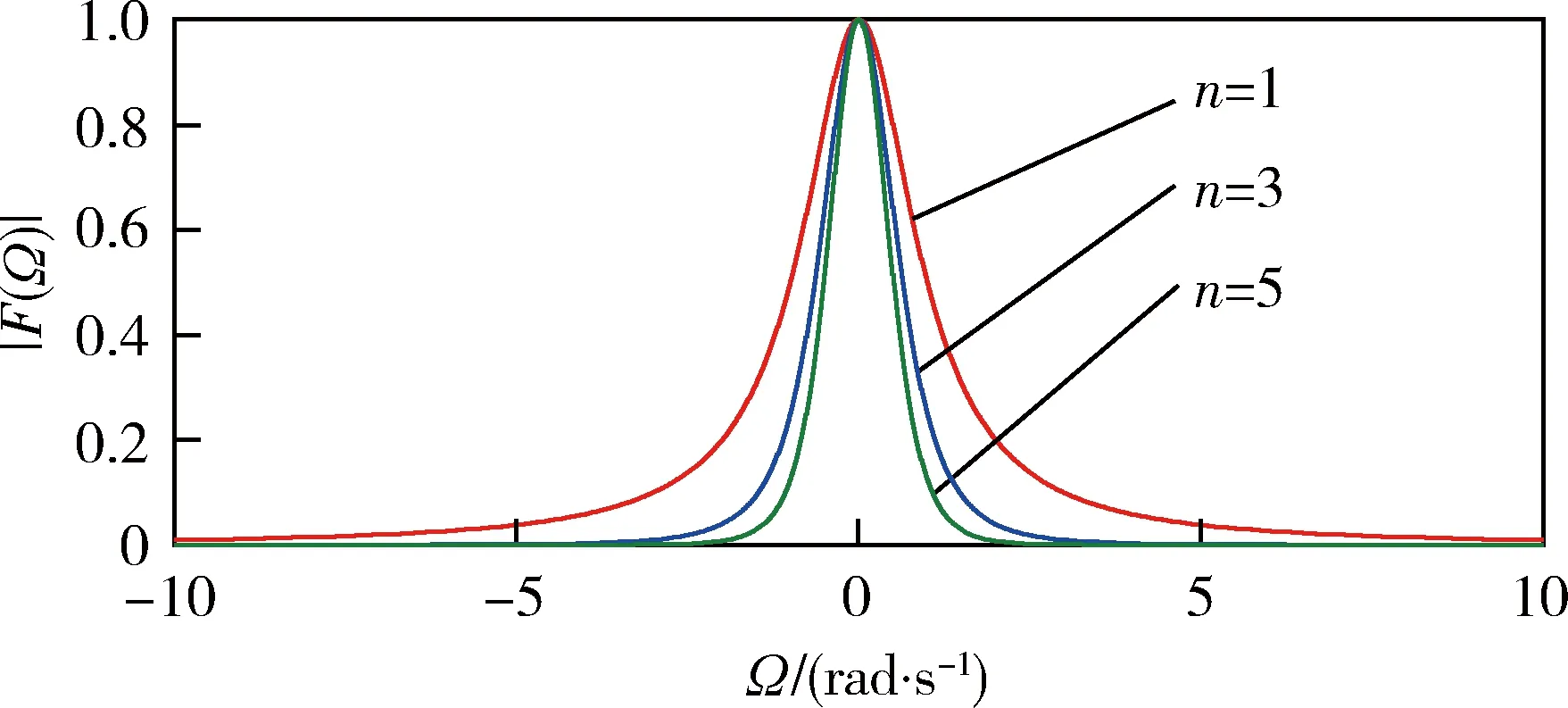
图2 不同n时的波形(a=1)
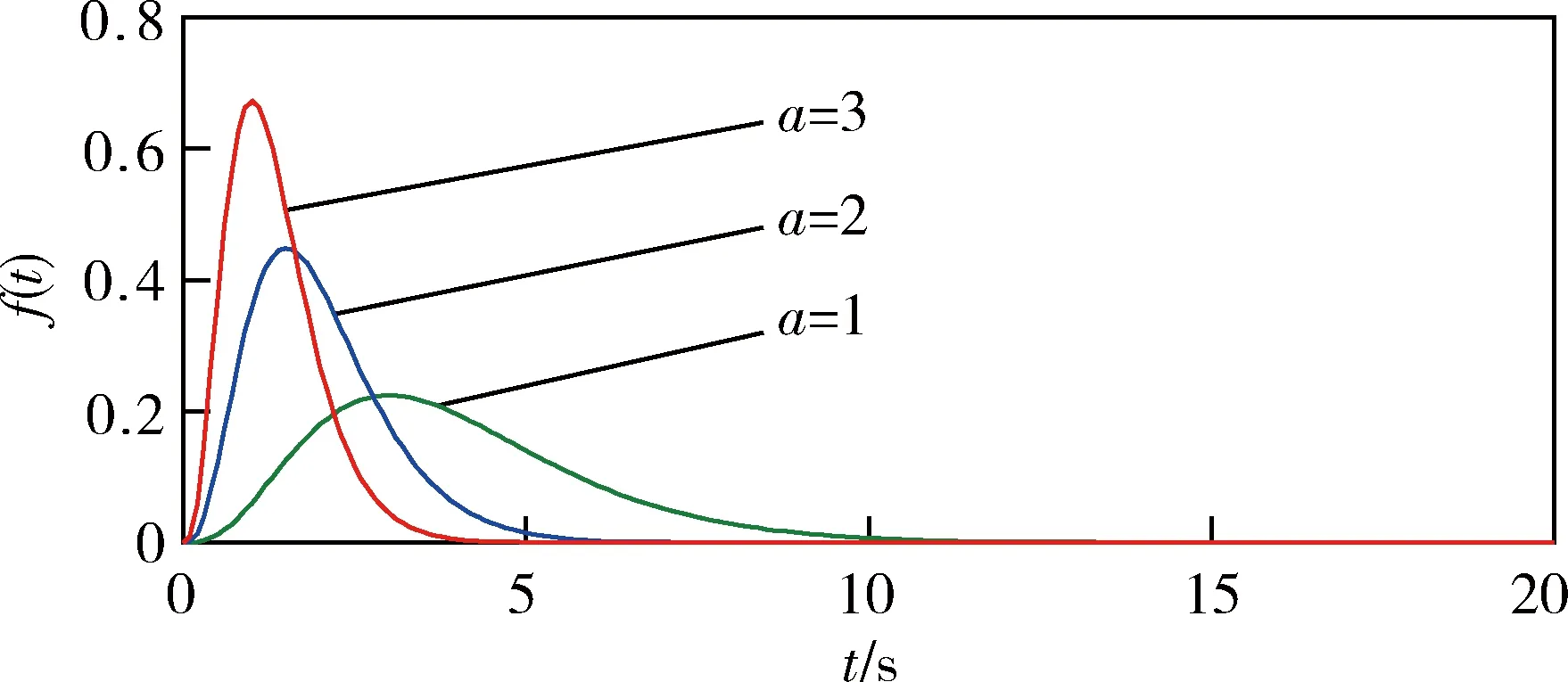
图3 不同a时f(t)的波形(n=3)
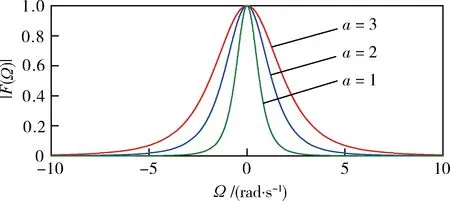
图4 不同a时的波形(n=3)
由图2、4可见:f(t)的频率成分主要集中在低频段,如果把f(t)看作是一滤波器的脉冲响应函数,则该滤波器具有低通特性;增大n或减小a可以减小频域带宽,提高频域集中性。f(t)的时宽和频宽同样满足Heisenberg不定原理,不可能同时达到最小。
在a一定的情况下,n过大时,时宽较大;反之,频宽较大。综合来看,n=3较为理想,故本文取n=3,此时式(4)变为
f(t)=a4t3e-at/6,a>0,
(7)
相应地,式(5)、(6)分别变为
(8)
(9)
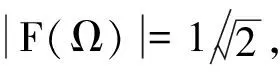
Ωc=(21/4-1)1/2a=0.435a,
(10)
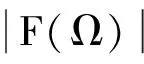
f(t)=0.291B4t3e-1.15Bt,B>0,
(11)
使得指数脉冲函数的时域表达式完全取决于其频域-3dB带宽B。相应地,式(8)、(9)分别变为
(12)
(13)
2 设计原理
2.1 复调制移频
将式(11)与一复正弦函数ejΩ0t相乘,记为
g(t)=f(t)ejΩ0t=0.291B4t3e-1.15BtejΩ0t,
(14)
当然,也可用cos(Ω0t)进行余弦调制[5]。由傅里叶变换的频移特性可知:时域上的复调制对应频域移位。由式(12)可直接得到g(t)的傅里叶变换为
(15)
其模为
(16)
相对于F(Ω),G(Ω)频谱的形状不变,但中心频率由0变为Ω0,相当于将F(Ω)平移至Ω0处,使G(Ω)具有带通特性。因此,g(t)可看作中心频率为Ω0、通带为(Ω0-Ωc,Ω0+Ωc)的带通滤波器。当Ω0=10rad/s、B=2rad/s时,g(t)的实部gR(t)、虚部gI(t)和|G(Ω)|的波形分别如图5-7所示。
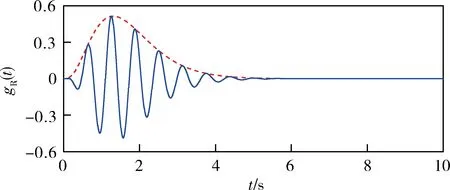
图5 gR(t)的波形
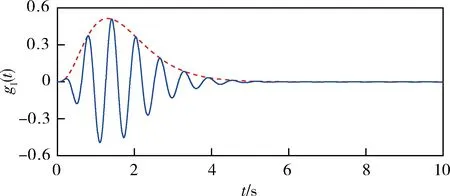
图6 gI(t)的波形
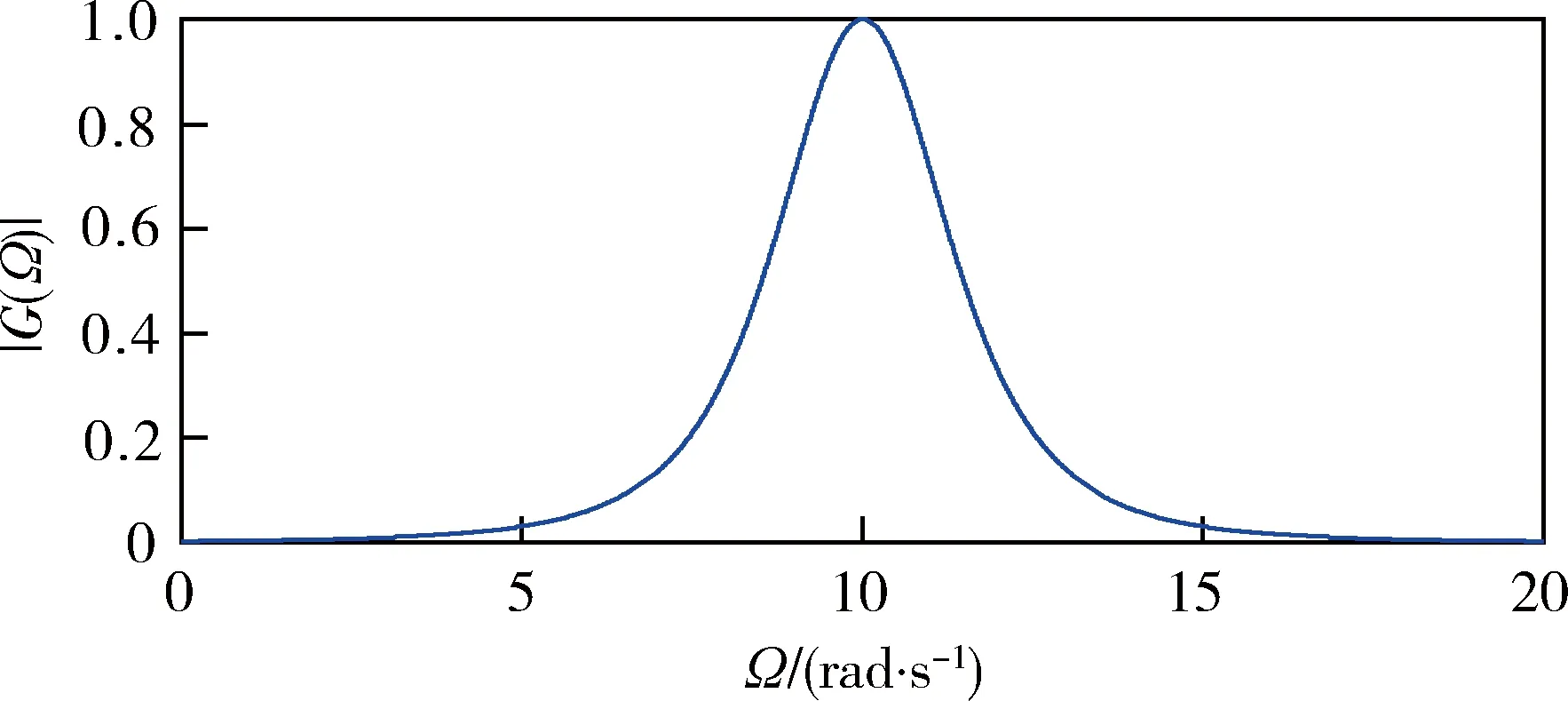
图的波形
2.2 滤波器组构建
将式(14)改写成
(17)
可得到一个由K个子滤波器组成,中心频率和带宽分别为Ωk、Bk的滤波器组,在信号处理中用于实现复杂信号的子带分解。如果保持Bk不变,则可实现恒带宽滤波器组的设计;如果使Bk和Ωk之间存在某种特定的关系(如恒带宽比),则可设计特殊用途的滤波器组,甚至用来设计梳状滤波器。
3 实现方法
gk(t)可近似为有限带宽、因果的IIR滤波器,其数字实现方法可利用冲激响应不变法:
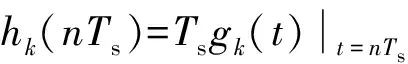
(18)
式中:Ts为采样时间间隔。
3.1 具体步骤
1)给定设计参数:子滤波器的个数K;采样频率fs,各子滤波器的中心频率fk和带宽bk(单位均为Hz)。由fk和bk分别得到中心频率Ωk=2πfk和带宽Bk=2πbk,k=1,2,…,K。
2)时间变量离散:给定滤波器的长度N,Ts=1/fs,t=nTs,n=0,1,…,N-1。
3)计算滤波器组各子滤波器的包络fk(n)、实部hR,k(n)和虚部hI,k(n):
可见:基于指数脉冲函数复调制的滤波器组设计方法简单快捷,计算量小,非常适用于滤波器组需要多次改变中心频率和带宽进行优化设计的场合。
3.2 注意事项
1)hk(n)是复解析的,如果使用实滤波器,可只计算hR,k(n),但系数要乘以2,以保证实滤波器的幅频特性通带幅值为1。
2)当fs一定时,N决定了滤波器的长度,可事先给定一个较小的阈值,N的取值要保证fk(N)小于该阈值,以使fk(n)有充分的衰减。
3)由于hR,k(n)、hI,k(n)的外形包络fk(n)关于极大值点是非对称的,利用卷积运算实现滤波处理时,为了使输出信号y(n)和输入信号x(n)的长度相同,需要计算fk(n)取得最大值时对应的位置,以3fs/(1.15Bk)取整后的取值为起点,从y(n)截取与x(n)相同长度的数据即可。
3.3 设计实例
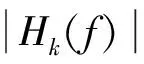

图8 恒带宽滤波器组各子滤波器的实系数
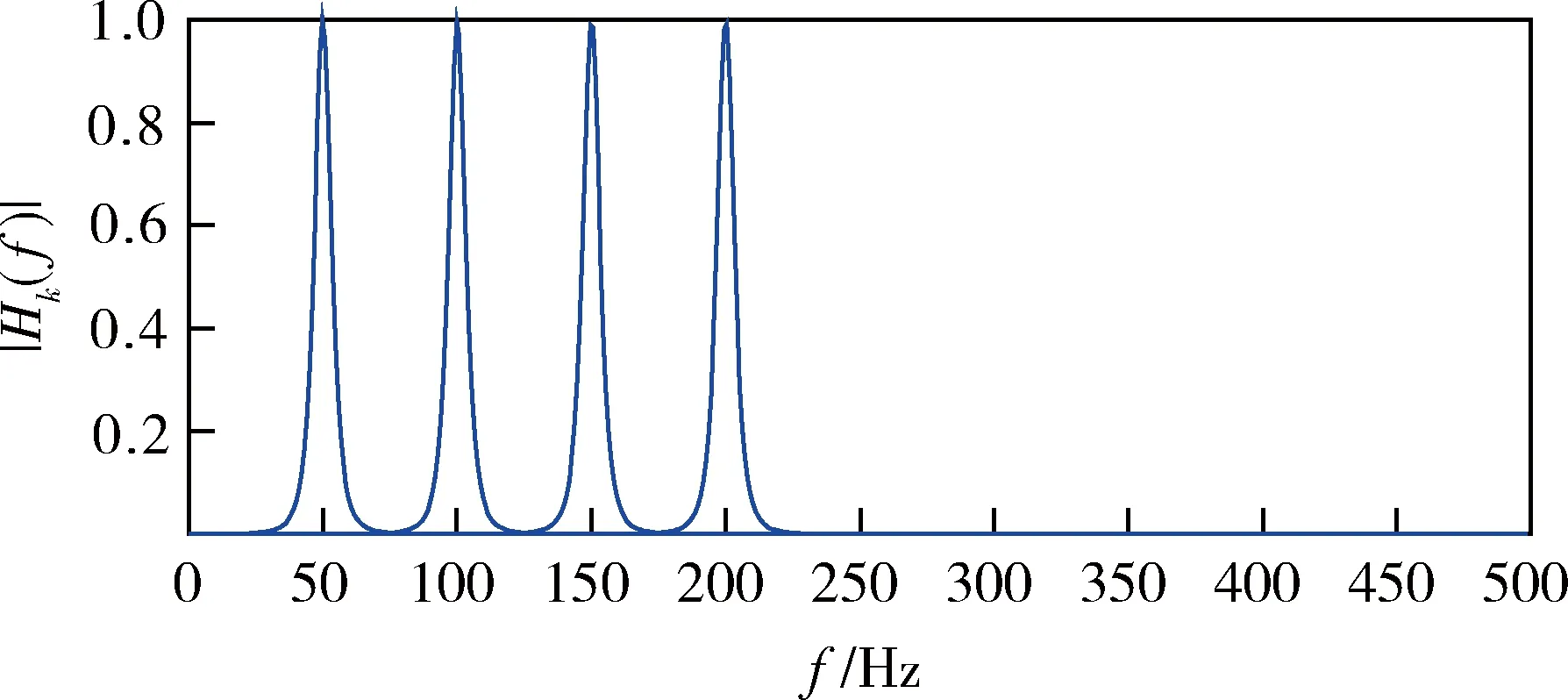
图9 恒带宽滤波器组的幅频特性
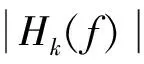
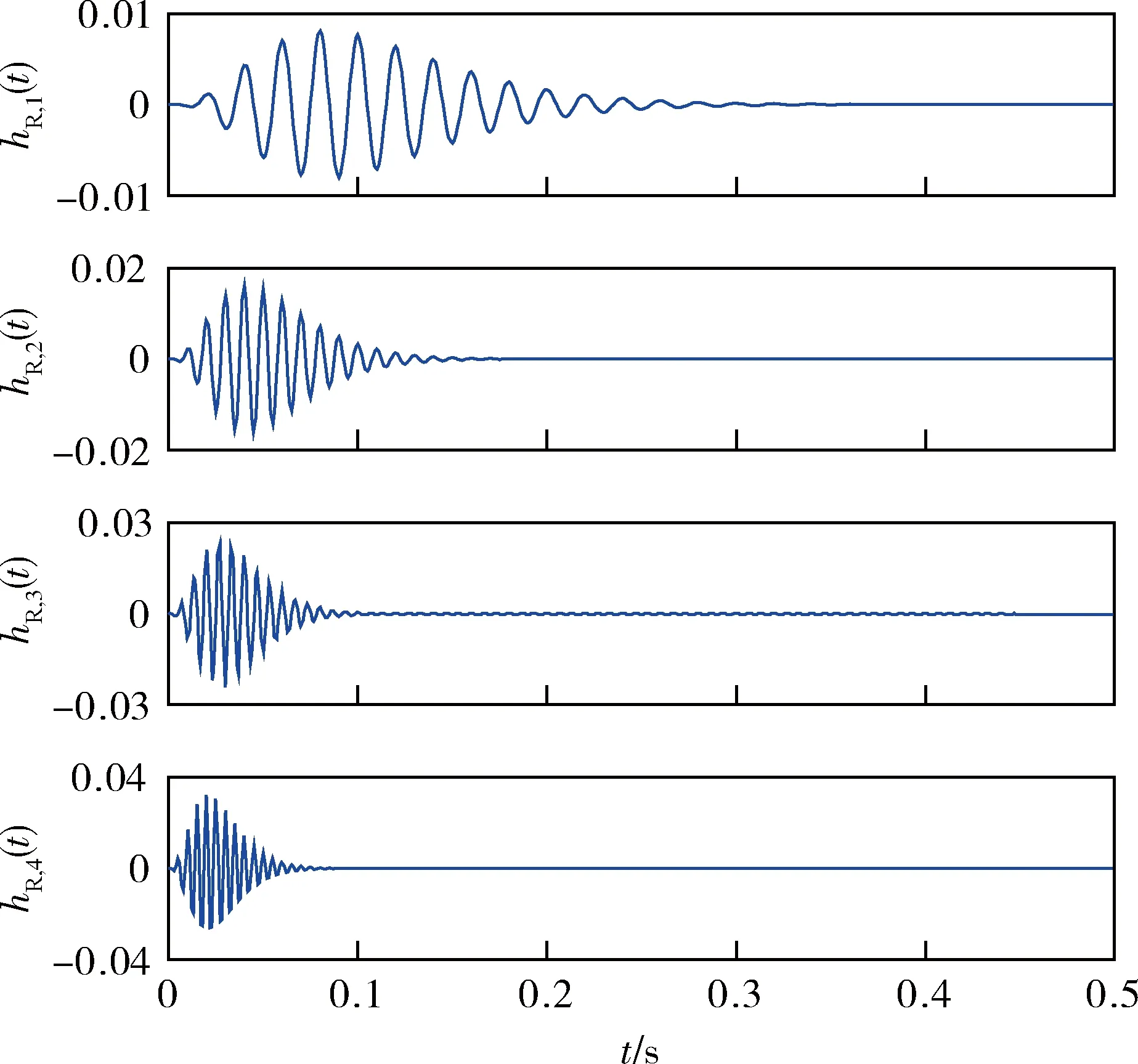
图10 恒带宽比滤波器组各子滤波器的实系数
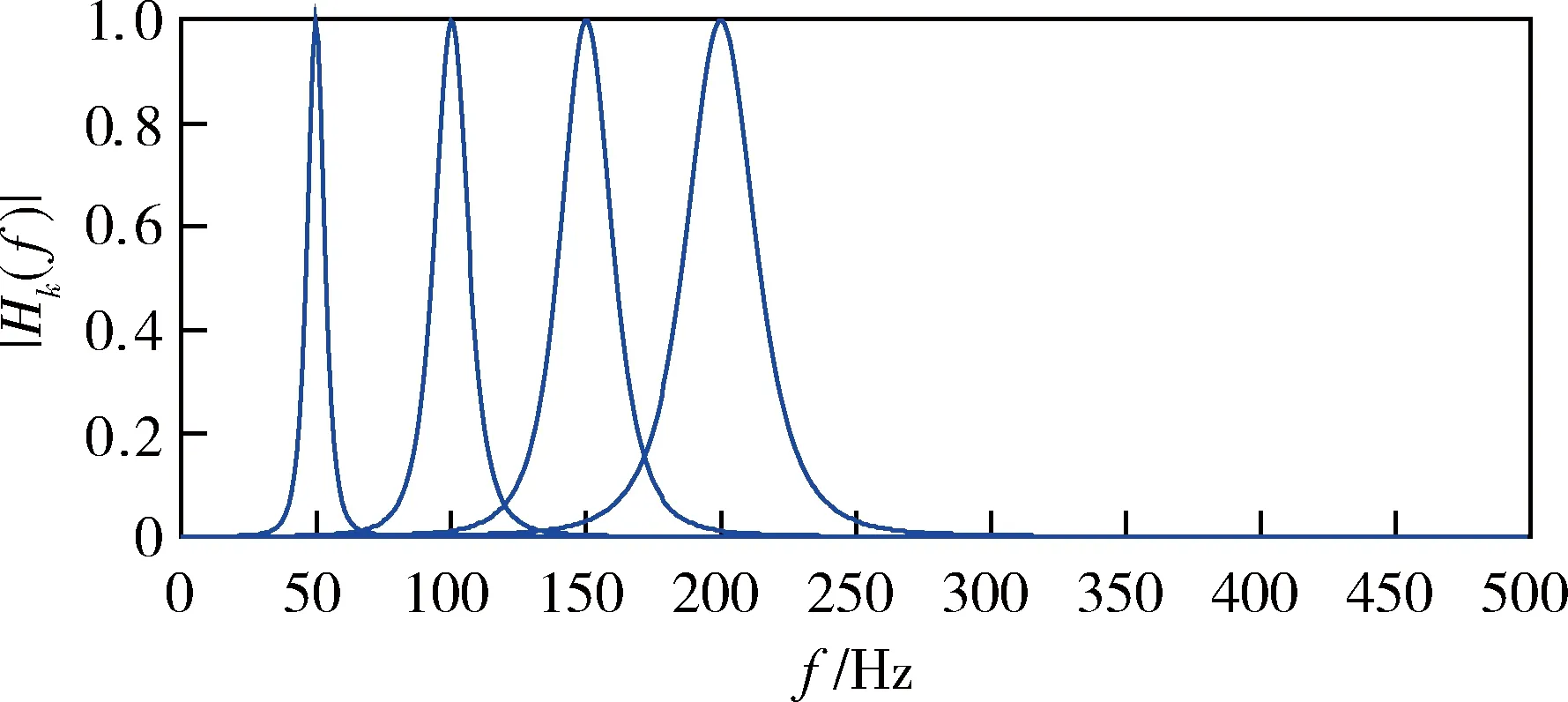
图11 恒带宽比滤波器组的幅频特性
由图8-11可见:恒带宽滤波器组由于各子滤波器带宽相同,各子滤波器实系数的外形包络也相同;而恒带宽比滤波器组由于各子滤波器带宽不同,各子滤波器实系数的外形包络也不同。
4 结论
1)指数脉冲函数具有简洁的表达式,合理选择参数n和a的取值,可使之在时域或频域具有较好的集中性。
2)取n=3,a=1.15B,经过修正后得到的指数脉冲函数时域表达式完全取决于其频域-3dB带宽,参数物理意义明确,更加便于应用。
3)滤波器的长度N取值要足够大,以保证滤波器系数有充分的衰减。
4)设计方法简单易行,只需给定各子滤波器的中心频率和带宽,即可设计不同用途的滤波器组。
[1] 赵越,赵晓晖,董倩.基于子带分解的自适应回声抵消算法[J].吉林大学学报,2009,39(1):198-203.
[2] 陈世雄,宫琴,金慧君.用Gammatone滤波器组仿真人耳基底膜特性[J].清华大学学报,2008,48(6):1044-1048.
[3] 胡峰松,曹孝玉.基于Gammatone滤波器的听觉特征提取[J].计算工程,2012,38(21):168-170.
[4] 高洪波,李允公,于良会,等.基于Gammatone滤波器组的齿轮系统侧隙诱发冲击特征[J].机械传动,2015,39(3):23-26.
[5] 樊新海,刘相波,张丽霞,等.基于组合复调制高斯函数的数字滤波器设计[J].装甲兵工程学院学报,2014,28(5):57-60.
(责任编辑: 尚彩娟)
Filter Bank Design Based on Complex Modulation of Exponential Pulse Function
FAN Xin-hai, ZHANG Chuan-qing, QIU Mian-hao, SUN Guo-qiang
(Department of Mechanical Engineering, Academy of Armored Force Engineering, Beijing 100072, China)
In view of the problem of filter bank design in digital signal processing, characteristics in time domain and frequency domain of exponential pulse function are studied and wieldy expression of time domain is gained after modifying exponential pulse function. Then a method of digital filter bank design is presented using complex modulation by appointing the center frequency and bandwidth of each sub filter, and its validity and practicability are verified by examples.
signal processing; digital filter bank design; exponential pulse function; complex modulation
2016-06-20
樊新海(1973-),男,副教授,博士。
TN713
:ADOI:10.3969/j.issn.1672-1497.2016.06.014
1672-1497(2016)06-0075-04

