基于混合极化架构的极化SAR:原理与应用 (中英文)
洪 文
(微波成像技术国家重点实验室 北京 100190)
(中国科学院电子学研究所 北京 100190)
(中国科学院大学 北京 100049)
基于混合极化架构的极化SAR:原理与应用 (中英文)
洪 文*
(微波成像技术国家重点实验室 北京 100190)
(中国科学院电子学研究所 北京 100190)
(中国科学院大学 北京 100049)
合成孔径雷达(Synthetic Aperture Radar, SAR)应用性能主要受限于同时获取高分辨与宽测绘幅宽的雷达图像的能力。而对于极化SAR(Polarimetric SAR, PolSAR)系统而言,其测绘幅宽更加受限。近年来,称为混合极化(Hybrid-Polarity, HP)架构的新型极化SAR架构吸引了广泛的注意。相比于传统的线性极化SAR,基于混合极化架构的极化SAR具有两点重要优势:更宽的测绘幅宽与更低的硬件要求。该文首先回顾了包括系统设计、系统模型与定标方法在内的混合极化架构相关原理。接着详细阐述了混合极化架构在定标与发射配置两个方面在工程实现中的难点并提出了一种改进型混合极化架构。与此同时,还介绍了以实验验证为目的而开发的原型实验系统。该文的后半部分回顾了适用于基于混合极化架构的极化SAR的相关应用。由于基于混合极化架构的极化SAR系统产生的全极化数据可以直接转换为传统的线性全极化数据,因此这一部分内容主要集中在对应的双极化应用,即简缩极化(Compact Polarimetry, CP)应用上。
合成孔径雷达;极化SAR;混合极化架构;简缩极化;定标;分类;简缩极化干涉SAR
1 引言
合成孔径雷达(Synthetic Aperture Radar, SAR)是一种可以通过信号处理技术合成地球表面高分辨率微波图像的主动成像雷达。它拥有全天时、全天候的成像能力。极化SAR(Polarimetric SAR, PolSAR)可以提供观测场景的一系列极化信息并已被成功应用于众多实际应用中[1,2]。目前,星载SAR系统的局限主要在于难以同时获取具备高分辨率与宽测绘幅宽的雷达图像。而对于可以获取散射目标完备极化信息的全极化(quadraturepolarimetric, quad-pol)SAR系统而言,其可获取的测绘幅宽相比一般的SAR系统更要小一倍以上。原因在于全极化SAR系统需要将脉冲重复频率(Pulse Repetition Frequency, PRF)至少提高一倍以上以满足交替发射两种互相垂直的极化波的需要。
传统的全极化SAR系统发射水平(Horizontal, H)与垂直(Vertical, V)线性极化波,同时使用H与V极化天线进行接收。这样的设置将会在大入射角时在交叉极化(HV或VH)测量通道中产生严重的距离模糊问题,进而进一步限制有效测绘幅宽[3,4]。另外,由于自然目标的同极化(HH或VV)散射回波能量通常比交叉极化散射回波能量高6~10 dB,需要在实际全极化SAR系统中应用复杂的接收策略来处理不同的极化通道接收到的能量,以保证接收到的回波信号均处于模拟数字转换器 (Analog to Digital, ADC) 模块的有效动态范围内[5,6]。针对以上问题,混合极化(Hybrid-Polarity, HP)架构于文献[4,7,8]中提出。混合极化架构下的全极化SAR系统交替发射右旋圆极化(Right-Handed Circular, RHC)与左旋圆极化(Left-Handed Circular, LHC)波,并使用正交的线性极化天线进行接收。这样,极化SAR系统中的发射极化波与接收极化波之间将不再存在同极化与交叉极化的关系,从而能够改善前述的距离模糊问题[4]。另外,极化SAR系统接收到的信号的平均能量是相当的,因而不再需要应用复杂的接收策略。这样,基于混合极化架构的全极化SAR系统相比传统的线性全极化SAR系统将拥有更宽的测绘幅宽与更低的硬件需求[4]。
混合极化架构还能够支持简缩极化(Compact Polarimetry, CP)中的圆发线收(Circular Transmit Linear Receive, CTLR)模式[7]。简缩极化是由不同特殊双极化(dual-polarimetric, dual-pol)模式组成的一个集合概念。它要求雷达系统发射拥有相同H与V分量的极化波,如左旋、右旋圆极化波与±45°斜线极化波,并保留接收极化波间的相对相位信息[9-12]。由于简缩极化具有双极化诸如双倍测绘幅宽、更低功耗与更简易系统需求[7,9]的优点,并在许多实际应用中能够得到与全极化SAR相当的数据处理结果[12-61],因而在过去的十年中广受关注。
以上这一系列优点使得混合极化架构成为未来完成极化SAR任务的潜在选择。截至目前为止已有数个极化SAR任务采用了混合极化架构。它们包括:搭载在印度Chandrayaan-1探月任务与美国月球勘测轨道飞行器(Lunar Reconnaissance Orbiter, LRO)上的两颗小型射频(mini-Radio-Frequency, mini-RF)雷达[62];搭载在印度遥感卫星RISAT-1上的C波段SAR[63];搭载在日本遥感卫星ALOS-2上的L波段SAR(实验模式)[64]。在未来,加拿大的C波段RADARSAT星座任务(RADARSAT Constellation Mission, RCM)[12,65,66],美国探测形变、生态结构与冰层动力学(Deformation, Ecosystem Structure, and Dynamics of Ice, DESDynI)遥感任务的L波段干涉SAR(Interferometry SAR, InSAR)系统[67,68]与印度的第2次探月任务Chandrayaan-2[69]亦已确认将采用混合极化架构。
本文首先回顾了混合极化架构的基本原理,包括系统设计、系统模型与标定方法。然后重点讨论了混合极化架构的两点问题。其中最主要的一点是当雷达系统工作在双极化模式下时,系统的发射失真即便被准确估计出来,也无法被标定。另外一点是在混合极化架构下,发射模式通常被设定为圆极化波。在这一设置下,极化SAR系统的双极化模式即为CTLR模式。但是在简缩极化中,除了CTLR模式以外,发射45°线性极化波的π/4模式在某些应用中同样可以得到较好的结果,因而同样值得关注。针对这两点,本文将提出一种混合极化架构的改进。同时,本文也将介绍以实验验证为目的而开发的原型实验系统。
本文在接下来的部分中将详述适用于混合极化架构的极化SAR应用。由于基于混合极化架构的极化SAR系统提供的全极化数据可以直接转化为传统的线性极化基散射矩阵,因此这一部分的综述主要集中在对应的双极化应用,即简缩极化应用上。首先这一部分将介绍4个常用的简缩极化信息提取方法,即协方差矩阵扩展方法,基于Stokes矩阵的方法,特征值分解方法与基于散射模型方法。接下来再介绍由这些信息提取方法衍生出的一系列简缩极化应用。考虑到文章的篇幅,本文仅对使用简缩极化数据的非监督地物分类应用与极化干涉树高反演应用进行详细综述。
本文的结构如下。第2节分别回顾了基于混合极化架构的双、全极化SAR系统的系统设计与系统模型。第3节阐述了混合极化架构的自检特性(selfchecking property)[7]以及有效标定技术。由于发射失真不能通过外定标方法进行标定,这一节还探讨了对发射失真的评估问题。第4节提出了一种混合极化架构的改进方案。第5节展示了多个数据处理算法,包括由混合极化基转换到线性极化基数据,及由全极化数据模拟简缩极化数据的算法。这一节还介绍了4个主要的简缩极化信息提取方法。第6节回顾了简缩极化应用。最后,第7节对阶段研究进行了总结。
2 混合极化架构
2.1 混合双极化架构
混合极化首先于文献[7]提出以支持简缩极化中的CTLR模式。CTLR模式要求雷达系统发射一种圆极化波(右旋圆极化或左旋圆极化之一)并使用正交的线性极化基进行接收。由于简缩极化实际上是由特殊双极化模式构成的一个集合概念,因此本文将此混合极化架构称作混合双极化(Hybrid Dual-Pol, HP2)架构。混合双极化架构的系统框图如图1 (a)所示。为了生成发射所需的圆极化波,波形发生器产生的信号首先经功分器分为两路功率相等的子信号,再将其中之一相移90°。两路生成的子信号随后被馈入双线性极化天线的H与V馈电口。这一部分设计在图中已使用虚线框标出。这一部分设计的简化框图如图1(b)所示。图中Si与So分别表示输入与输出端口输入的信号,而At与Ar分别表示连接发射与接收天线的不同馈电端。如果发射与接收均使用同一双线性极化天线,则
可以看到,混合双极化架构中并没有过多的射频硬件。这意味着雷达系统中的损耗以及失真源将会更少。另外,由于两路接收通道均不再需要接收交叉极化信号,因此其平均信号水平应相当。这也意味着雷达系统中出现较强极化信号污染较弱极化信号(即发生系统串扰)的概率变小了[4]。

图1 混合双极化架构的系统框图 (Raney 2007, 文献[7])Fig. 1 Block schematic of the HP2 architecture (Raney 2007, Ref. [7])
基于混合双极化架构的星载极化SAR系统的系统模型为[70]:

其中M是测量散射矩阵,S是真实散射矩阵,RF代表单程法拉第旋转(Faraday Rotation, FR)矩阵,RF中的Ω是法拉第旋转角,R是接收失真矩阵,N是各测量值中的加性噪声项。M中的下标表示右旋圆极化极化发射并使用H与V极化接收。R中包括了接收的串扰项δ1与δ2和通道失衡项f1。kRHC与kLHC分别是右旋圆极化与左旋圆极化的Jones矢量,而δ是右旋圆极化发射时的综合串扰。实系数A代表受距离r与俯仰角φ影响的总增益项。复系数ejφ代表双程相位延迟和与系统相关的相位影响。
照射到目标表面的电磁场Ei可以被进一步表示为:

可以看到,如果发射的圆极化波是完美的话,即δ=0, 则FR可在后续的处理中忽略。即使发射的极化波是非完美的,FR对基于混合双极化架构的极化SAR系统产生的影响也应比传统线性极化SAR系统小。
虽然发射失真可以如式(1)与式(2)一样直接使用单一项δ综合表示,它们同样可以使用传统发射失真矩阵T来表示[71]:

其中δ3,δ4, 与f2分别是发射通道串扰与通道失衡项。这些失真项与综合串扰项之间的关系为[72]:

其中
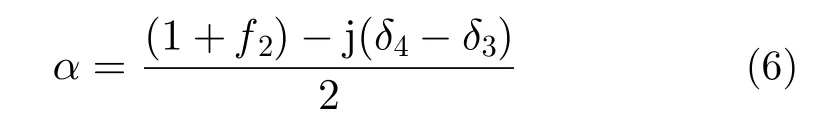
发射失真的两种表示方法均是有效的。但由式(1)可知,即便精确知道发射失真项的大小也无法通过右乘对应逆矩阵来得到目标的真实散射矩阵。因此使用综合串扰项统一表示所有发射失真会更加简洁明了,而精确的发射失真表示可以更详细地分析不同失真源的影响。这一部分工作将在3.2节中进行回顾。
2.2 混合四极化架构
文献[7]建议使用混合极化架构代替传统的线性全极化系统来构建全极化SAR系统。这样的设置下,雷达系统将交替发射左右旋圆极化波,使用H, V极化基进行相干接收。这一想法在文献[4]与[8]中被进一步详细阐述。
图2(a)中展示了混合四极化架构(Hybrid Quad-Pol, HP4)[8]的系统框图。发射模块中的移相器相较前述混合双极化架构做了一点小的修改。为了分别发射右旋与左旋圆极化波,信号的相位分别相移+90°与-90°。这一部分设计同样在图2(a)中使用虚线标注出来了,并在图2(b)中展示了其简化框图。如果移相器固定相移+90°或-90°,则得到的系统设计即为混合双极化架构。因此CTLR模式可以视作基于混合四极化架构的极化SAR系统的对应双极化模式。后文将使用混合极化架构一词来指代本节介绍的混合四极化架构。
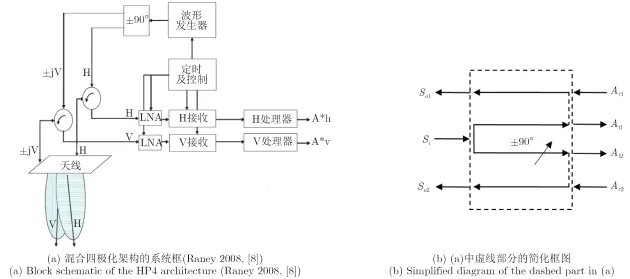
图2 混合四极化架构的系统框图 (Raney 2008, 文献[8])Fig. 2 Block schematic of the HP4 architecture (Raney 2008, Ref. [8])
混合四极化架构同样继承了前文所述混合双极化架构的各优点。首先,发射与接收极化之间同样不再存在同或交叉极化的关系。根据文献[4]中的推导结果,这一特性可以有效减小距离模糊,从而使得基于混合极化架构的极化SAR系统拥有更宽的测绘幅宽。另外,由于接收通道的平均信号能量应是相同的,因此不再需要复杂的接收策略来调整不同回波信号的接收增益[5,6]。这样,相比传统的线性极化系统,基于混合极化架构的极化SAR系统的系统设计更简单。这意味着通过混合极化架构,雷达的成本得以降低并且能够更好地保证标定与测试的鲁棒性。
由于不再需要根据不同的雷达回波改变接收机的接收增益,基于混合极化架构的星载极化SAR系统的系统模型与考虑了FR效应的标准极化系统模型相似[73]:
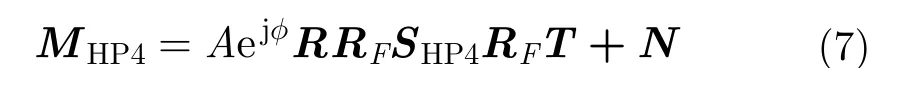
其中MHP4是2×2的测量矩阵,SHP4是一个包括了真实散射矩阵S元素的2×2矩阵。SHP4与S中的元素之间的关系为:
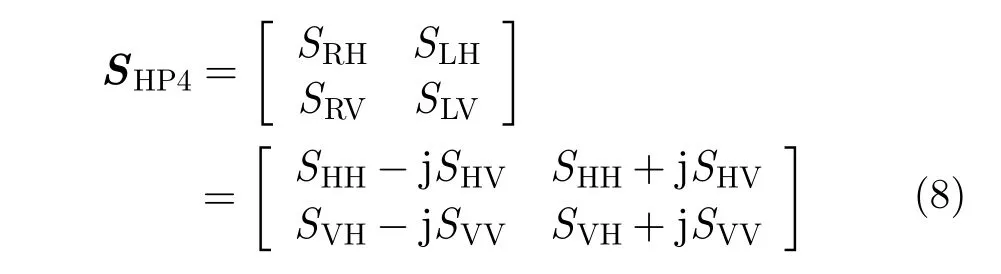
由基于混合极化架构的极化SAR系统获得的测试数据同样可以首先转化为线性极化基,再直接应用标准极化系统模型进行后续的定标与数据处理。
3 失真的标定与评估
基于混合极化架构的极化SAR获取的全极化数据可以直接转化为传统的线性极化基,因此可以直接应用标准的极化定标技术进行数据标定工作。混合极化架构在定标方面剩下的问题是如何标定获取的双极化数据,即简缩极化数据的标定。
3.1 简缩极化数据的标定
3.1.1 自检定标方法基于混合极化架构的极化SAR系统的两路接收通道的平均信号能量应是相等的,因此当回波信号的H与V分量相等时,相应的接收信号的1阶与2阶统计特性也应是相等的。在实践中,当雷达垂直观测地表时能够满足此条件。假设没有发射失真,则不满足此判定标准的误差可被测量与补偿[7,74].
对于月球探测而言,由于既无法在月球表面放置定标器,月球表面又没有亚马逊热带雨林,无法使用对地遥感中常用的定标方法。因此在mini-RF探月任务中使用了上述的混合极化架构定标方法[62,75]。在其在轨定标实验中,航天器被人为调整使得雷达天线能够对准月球的天底点。测得的VH通道间增益与相位差分别为-2.55 dB±0.25 dB与-138°。这一测试结果较好地吻合了端到端的系统测试得到的预期结果-2.14 dB±0.25 dB与-135.9°±1.5°。两者存在细微差别的主要原因在于实际发射的极化波并非是完美的圆极化波,而是轴比(Axial, Ratio, AR)为2.46 dB±0.15 dB的椭圆极化波。
3.1.2 基于全极化系统的定标方法基于混合极化架构的极化SAR系统既可以工作在双极化模式下,又可以工作在全极化模式下。因此雷达系统如果能够如星载SAR一般,在整个数据获取阶段保证系统的稳定性,则系统的误差可以通过在各数据获取阶段的开始与(/或)结尾使用全极化模式来得到[70]。
3.1.3 法拉第旋转角的标定方法对于工作在低频段的星载极化SAR,还需要考虑FR效应的影响。除了使用电离层总电子含量(Total Electron Content, TEC)图来估计FR角大小的方法外[76], FR角还可以通过理论上HH-VV相位差接近零的裸土后向散射估计[18]。 裸土的识别是通过不受FR影响的一致性系数μ来完成的:
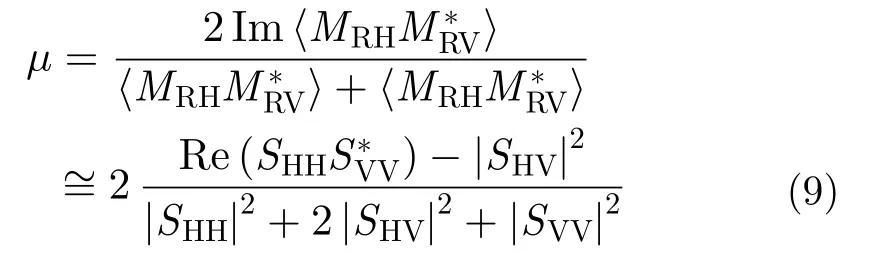
对于裸土散射(即表面散射)而言,μ是正数且趋近于1。对于2次散射而言,μ是负数且趋近于-1,其中间值(零值附近)代表着体散射。体散射与表面散射之间的阙值估计为0.35,而体散射与2次散射之间的阙值估计为-0.2。通过识别出的裸土,FR角可通过以下公式计算得到:

3.1.4 基于定标器的标定方法在文献[77]中,My-Linh等人首先针对CTLR模式提出了基于定标器的定标方法。由于发射失真无法被标定,雷达系统的发射被认为是完美的(即无误差的)。该方法使用了包括两个0°与45°的二面角与一个0°三面角的3个定标器来标定接收的通道失衡与通道串扰,FR角和系统增益。
文献[78]中,Chen与Quegan研究了针对工作在CTLR模式下的低波段星载SAR系统基于定标器的定标方法。在其研究中共分析了6种包含由数量不等的主动与被动定标器组成的定标策略。首先可以确认的一点是,使用4个定标器的定标策略比仅使用3个定标器的定标策略准确性更高。但这会在实际部署中增加花费与复杂程度。另外一点结论是,在所有被动定标器中首选网格三面角(gridded trihedral)定标器。相比二面角与三面角定标器,它的平均极化噪声(Average Polarimetric Noise, APN)更低且对瞄准精度不敏感。文献[78]最终推荐的定标策略包括2个区分HH与VV通道的网格三面角定标器以及2个能够区分HV与VH通道的主动定标器。
在文献[79]中,陈琳等人提出来一项针对所有双极化SAR系统的通用定标算法。该算法仅使用了1个三面角与2个0°与45°二面角。这一方法中未考虑FR的影响。经验证,此通用定标算法对所有双极化模式,包括传统的线性双极化模式以及简缩极化中的CTLR模式与π/4模式均有效。最终该算法的有效性在配置了π/4模式与CTLR模式发射/接收设置的地基SAR系统上得以验证[34]。
3.2 发射失真的评估
在上述章节中,本文已讨论了混合极化架构在工程实现中的难点:双极化模式下的发射失真并不能简单通过乘上一对应逆矩阵消除。因此应当对发射失真产生的影响进行完整的评估。在文献[71]中,Guo等人采用了最大归一化误差(Maximum Normalized Error, MNE)指标对发射失真做了定量评估。对于基于混合双极化架构的极化SAR系统而言,MNE的定义为:

这一评估方法可以用来评估由FR、通道失衡以及通道串扰等多重误差源综合产生的影响。但是为了单独评估各误差源的影响,下文将分别仿真由各误差源单独引起的MNE变化。
3.2.1 法拉第旋转角根据式(3),当FR是发射中唯一的失真,即发射的是完美圆极化波时,FR角直接变为一项可被省略的加性相位项。如果发射极化波是非完美的,则FR将会如式(3)所示,对综合串扰δ产生影响。
3.2.2 通道失衡假设发射中唯一存在的失真为通道失衡,即图3中展示了的由H与V通道增益与相对相位差引起的MNE变化轮廓线。为了维持MNE小于-20 dB,椭圆分界线大约为增益±1.2 dB,相位偏移±8°。
3.2.3通道串扰为了简便,假设通道串扰满足并且没有其他失真源。实验结果表明通道串扰的相位偏移对MNE没有影响。因此仅评估通道串扰增益带来的影响。评估结果如图4所示。

图3 由通道失衡引起的MNE变化Fig. 3 MNE evaluation due to channel imbalance
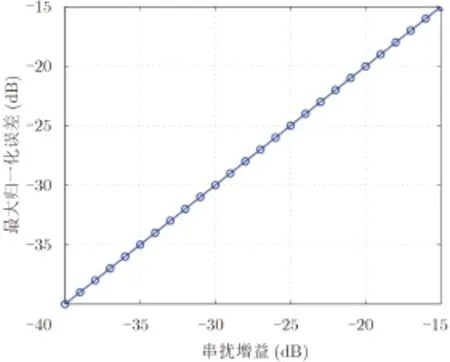
图4 由通道串扰增益引起的MNE变化Fig. 4 MNE evaluation due to crosstalk gain
可以看到,MNE随着通道串扰增益按比例以分贝级增长。为了维持MNE小于-20 dB,发射的通道串扰需要小于-20 dB。
3.2.4 入射角发射波的非圆性(non circularity)同样会随着入射角的变化而变化[65]。在文献[65]中,Touzi与Charbonneau估计RCM发射极化波的AR的变化范围会在1.4 dB(在0°波束扫描角50 km范围内)到3 dB(ScanSAR模式下,350 km幅宽)之间。为了估计这一影响,发射Jones矢量被设置为[81]:

其中,φ∈[-/2;/2]是极化椭圆的椭圆方向角,而|τ|∈[0;/4]是极化椭圆的椭圆孔径,也称椭圆率角。
这里仅考虑椭圆率,因此方向角被设为φ=0。评估结果如图5所示。可以看到,MNE随着椭圆角偏离理想值(45°)而增大。为了维持MNE小于-20 dB,椭圆孔径的偏离值需在[-5°, 5°]范围内。当椭圆孔径小于Touzi与Charbonneau估计的最差值35°时,MNE大约为-15 dB。
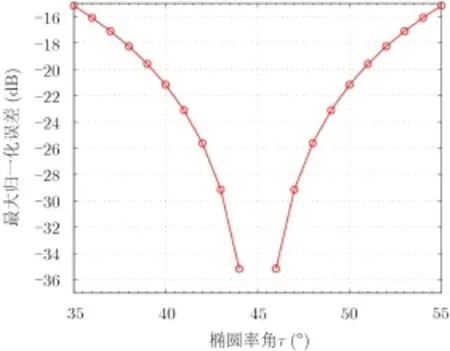
图5 由椭圆率引起的MNE变化Fig. 5 MNE evaluation due to the change in ellipticity
4 改进型混合极化架构
4.1 系统设计
如前所述,混合极化架构在工程实现中,定标方面的主要难点是:当工作在双极化模式下时,即使能够通过不同的外定标方法精确得到发射失真的大小,也无法对发射失真进行标定。因此在大部分的混合极化系统相关文章中,发射失真是被忽略的。但是正如3.3节所述,发射失真一定会对基于混合极化架构的极化SAR产生影响。
在3.3节中使用了用来测量极化系统极化纯度的通用度量MNE来评估发射失真。与此同时,发射失真也可以通过它们所产生的结果,即发射极化波的失真大小来度量。在这一观点下,可以使用AR来量化发射失真。对于完美圆极化而言AR=0 dB,而AR=+∞则表示的是线性极化波。据报道,两颗探月小型射频雷达的AR大约为2.5 dB[62]。而即将发射的RCM雷达系统在最坏情况下的AR约在1.5 dB到3.0 dB之间[65]。印度的第2次探月任务规划其所使用的雷达系统AR小于2.0 dB[69]。据研究,AR与MNE在数值上并非是一一对应的。如要保证前述MNE-20dB标准,AR需小于1.8 dB。
为了克服上述问题,需要在基于混合极化架构的极化SAR系统中应用内定标技术。然而传统的内定标回路将会增加雷达系统所需的射频器件数量。这不仅会导致系统成本的增加,同时还将增加系统中潜在的失真源的数量。因此本文采取另一种方案,仅修改混合极化架构中的发射模块。修改后得到的改进型混合极化架构的系统框图如图6(a)所示。修改后的发射模块同样在图6(a)中使用虚线标注出来了,并在图6(b)中展示了其简化框图。对比图1 (b)与图2(b)中所示的系统设计,原始的±90°移相器由2个高精度可调衰减器与360°移相器代替。在图6(b)中,这两个器件分别被表示为“A”与“P”。
应用这一直观的改进,可以使用预失真的方法来修正发射失真:首先,调节衰减器与移相器,使得两路发射通道拥有相等的能量与期望的相位差(例如对于圆极化而言,90°或-90°)。接下来使用之前章节介绍的定标方法测定发射失真大小。然后,继续调节衰减器与移相器以补偿测定的失真。这样,就可以将发射失真降低到一能够被接受的水平上。
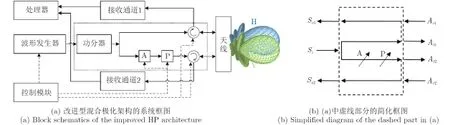
图6 改进型混合极化架构的系统框图Fig. 6 Block schematic of the improved HP architecture
利用这两个高精度可调衰减器与移相器,基于改进型混合极化架构的极化SAR系统同时还可以产生任意的发射极化波。考虑到降低FR效应与消除观测中的旋转选择性(rotational selectivity),原始的基于混合极化架构的极化SAR系统通常使用圆极化波作为发射极化波。然而其他发射设置同样值得进一步的研究与应用。例如,文献[29]发现π/4模式的数据可以应用基于模型的目标分解方法,从而获得比CTLR模式更好的极化分解结果。类似的算法同样可以应用到π/4模式下的简缩极化干涉SAR(PolSAR interferometry, PolInSAR)数据处理中并且得到较好的目标分解结果[31]。
类似于最初的混合极化架构,改进型混合极化架构同样能够支持全极化模式。通过转换衰减器与移相器,改进型混合极化架构可以交替产生互相正交的极化对。虽然基于改进混合极化架构的极化SAR理论上可以生成任意的极化对,但是为了保留拥有更宽测绘幅宽的优势,最终采用的发射极化基需与接收极化基(即H与V极化基)不同[4]。
4.2 系统模型
2.1节与2.2节中介绍的系统模型同样适用于基于改进型混合极化架构的极化SAR系统。但是需要注意的是,当工作在双极化模式下时,式(1)与式(2)中发射极化波带有综合串扰项δ的Jones矢量需要相应做出调整。例如,若发射采用的是传统的H与V极化波,或者前述的斜线性极化波,则该项需调整为[79]:
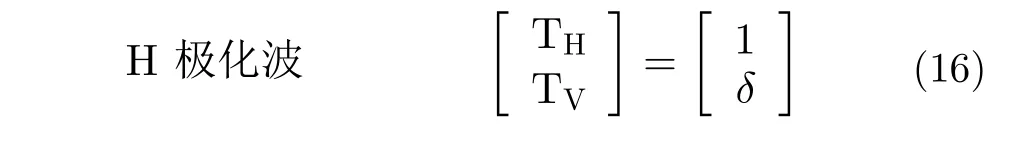

而对于全极化模式,式(7)中的2×2矩阵SHPA需要根据采用的发射与接收极化基做出相应的调整。
4.3 原型系统
图7展示的是包含发射与接收模块的改进混合极化架构原型系统。矢量网络分析仪(Vector Network Analyzer, VNA)被用于测量原型系统各通道的幅度与相位特征。通过相应的控制程序可以实现对原型系统中的不同器件的控制。该程序还可以通过网络与VNA进行通信实现数据的自动采集。最后,该程序集成了前述的预失真功能。据估算,利用预失真方法可以将理想双极化天线产生的圆极化波的AR控制在1 dB以内。
另一个需要探讨的问题是不同天线的使用问题。最初的混合极化架构建议利用同一个双线性极化天线来发射和接收极化波。但是同样可以使用两个互相垂直的单极化天线来代替双线性极化天线。如果不使用相同的天线进行发射与接收,则需要多达4个单极化天线。在后续的研究中,拟采用这一包含4个单极化天线的天线设置方案。这样的设置方案主要拥有成本低与隔离度高这两项点优点。但是与此同时,这样的设置会因为采用两个不同天线同时发射或者接收,而产生视差问题(parallax problem)。具体问题仍需进一步研究。

图7 使用VNA测试的改进混合极化架构的原型系统Fig. 7 Prototype system of the improved HP architecture measured by a VNA
利用这一原型系统,可以首先验证预失真方法,并开展更多不同简缩极化模式的相关实验、分析发射失真对雷达观测产生的实际影响。改进混合极化架构的数据分析问题可以采用Sabry与Vanchon[82]针对一般简缩极化与全极化SAR研发的数据分析框架。
5 数据处理方法
根据雷达极化的基本理论[81],任意全极化数据均可以直接转换成其他发射/接收设置下的极化数据,包括双极化模式数据。因此通过基于混合极化架构的极化SAR系统采集到的全极化数据可以直接转化为传统的线性全极化数据。这样便可以直接应用为传统极化SAR研发的一系列数据分析方法。
混合极化架构对应的双极化模式,即简缩极化模式是最近十年才提出的。其数据处理方法以及应用仍值得回顾。由于前文介绍的改进型混合极化架构同时可以产生CTLR模式以及π/4模式的数据,因此在接下来的两节中将主要介绍它们对应的数据处理方法以及应用。
5.1 简缩极化数据仿真
截至目前为止,仅有印度的RISAT-1与日本的ALOS-2卫星有能力提供实际的简缩极化数据。其中,后者以实验模式进行的简缩极化模式数据获取并未公开。因此目前绝大部分简缩极化研究仍是基于所谓的模拟(simulated)简缩极化数据展开的。模拟简缩极化数据指的是前文所述由全极化数据直接转化得到的相应双极化数据。文献[7]中的附录部分列举了由线性全极化数据转化模拟CTLR模式数据的方法。该方法利用的是传统线性全极化数据的协方差矩阵C3。类似地,也可使用相干矩阵T3模拟简缩极化数据[83]。文献[11]中展示了所有3种主要简缩极化模式由2×2散射矩阵元素构成的散射矢量与协方差矩阵。这一转化过程同样可以直接使用最新的PolSAR Pro 5.0软件[84]来完成。
需要注意的一点是,虽然本文将这种转化得到的数据称为模拟数据,但是由于使用的数据是真实数据,转化得到的数据同样也是真实数据。另外,由于转化得到的简缩极化数据与全极化数据本质上使用的是同一组数据,因此基于这两组数据之间的对比是可重复的。
5.2 基本数据产品
简缩极化数据的基本数据产品包括2×2协方差矩阵C2与Stokes矢量
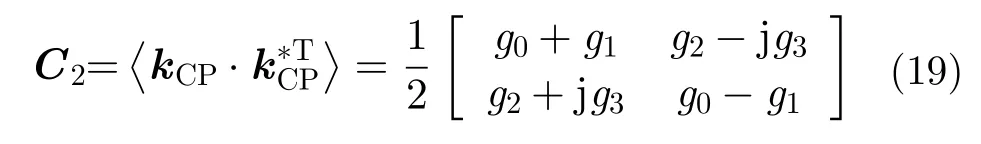
其中〈·〉函数表示的是空间平均,kCP是不同简缩极化模式的散射矢量,而*T则表示共轭转置。根据一系列基于蒙特卡罗(Monte Carlo)仿真的研究[38,40,71],公式(19)中的空间平均至少需要49视(一7×7 矩形滤波或拥有相等视数的其他滤波器)以保证后续处理得到的子参数是可靠的。这些数据产品可以使用下文介绍的方法进行后续处理。
5.3 简缩极化信息提取方法
5.3.1 协方差矩阵扩展方法根据文献[11],3种主要简缩极化模式的协方差矩阵均由以下3项相加构成:第1项包含的是仅与SHH和SVV有关的元素,第2项包含|SHH|2元素,而最后一项包含的是交叉极化相关项。基于互易假设SVH=SHV与反射对称假设中的未知数可被简化到仅剩5个标量,即|SHH|2, |SHV|2, |SVV|2和的实部与虚部。如果还能进一步找到这5个标量间的限制条件,则C2可被扩展为传统的3×3协方差矩阵C3。扩展得到的协方差矩阵也被称为伪全极化数据。文献[9]中假设的限制条件为:

利用这些限制条件,可以通过迭代解出|SHV|2这样,伪全极化数据中的其他未知项便可通过计算得到。除此方法之外,还有基于散射分解模型[48,85]或C2的特征值或极化度(Degree of Polarization, DoP)的重建算法[86,87]。文献[87]中详细对比、评估了这些算法。
这一类信息提取方法的优点在于一旦得到了伪全极化数据,则可以直接应用传统全极化SAR的数据分析方法。但是极化SAR中大部分的应用需要的是得到观测场景的散射特性,而不是事先对它们做出一定的假设。因此这一类方法的应用实际上是非常受限的。
5.3.2 基于Stokes矢量的方法简缩极化数种的极化信息还可以从SV中直接进行提取。通过SV可以进一步得到一系列包含不同极化特性的子参数[7,62,88]:
前文所述的极化度DoP:
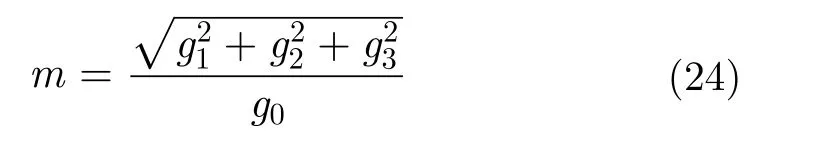
线性极化度mL:
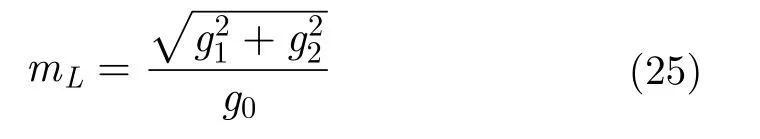
线性极化比:μL

圆极化度mC:

圆极化比(Circular Polarization Ratio, CPR)μC:

后向散射场的两个线性电矢量间的相对相位δ

除去这6个子参数,SV中还能提取另外两个非常重要的参量:从简缩地表随机体散射(Random Volume over Ground, RVoG)散射模型中提取出的目标参数αs[84]与庞加莱(Poincaré)椭圆率参数χ[89,90]。
在文献[84]中,简缩RVoG散射模型的形式如下:

其中上下标分别代表左旋圆极化与右旋圆极化发射。对应的目标参数为:
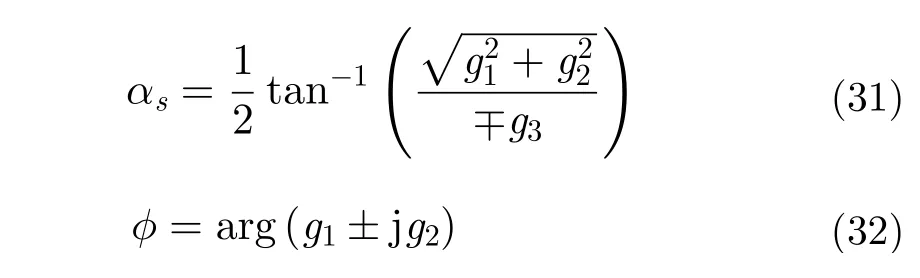
可以看到,在简缩极化RVoG散射模型中,SV被分解为两个独立项,一个代表随机体散射,而另一个代表极化表面散射或地表成分。
根据著名的Born-Wolf电磁波分解式[82],SV同样可以被分解为一个完全极化分量与一个完全去极化分量。其中完全极化项可以进一步写成由庞加莱参数,即方向角ψ与椭圆率角χ构成的形式:

对比式(30)与式(33)所表示的分解模型,可以发现φ=ψ, 而αs与椭圆率之间的关系为:
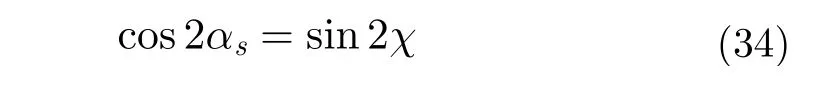
这两个参数与前文提及的相对相位δ通常被用作表面散射与2次散射之间的指示器。但是由于δ会受方向角ψ影响,因而简缩极化分解与分类算法中更常使用αs与χ。
5.3.3 基于特征值分解的方法与著名的H/alpha分解算法类似,C2同样可以直接使用特征值分解算法进行分解[40,84,91]:

其中,λi与i分别是的特征值与单位特征矢量。进一步得到电磁波熵Hw与散射角α:
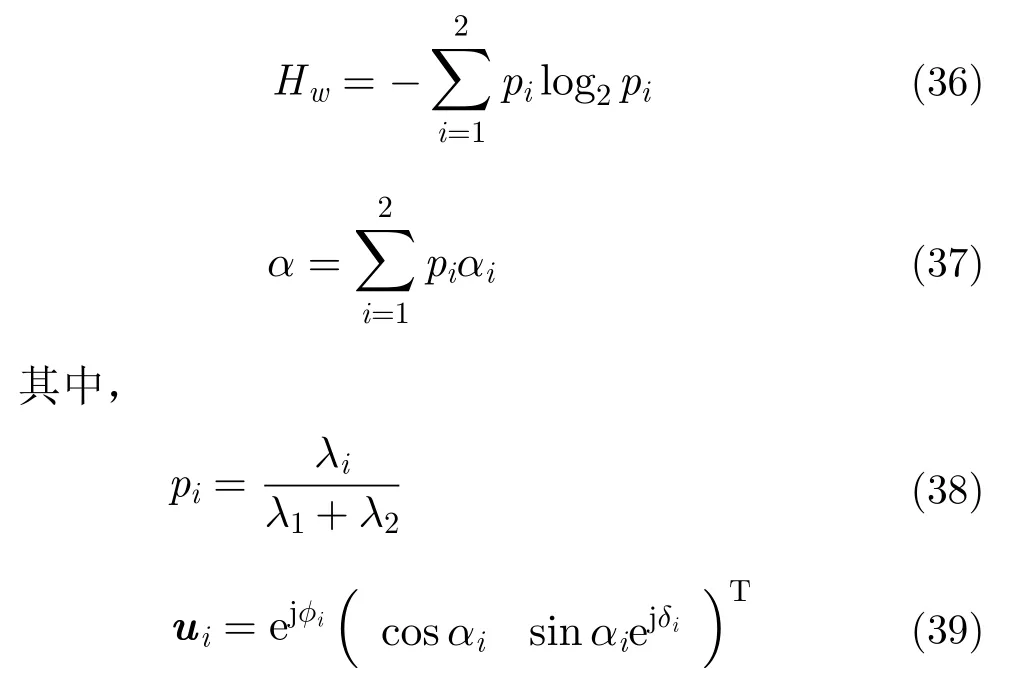
Hw/α平面的边界曲线可以通过设为:

得到。文献[40]结合了数个星载与机载平台的极化数据,得到了不同极化散射机制(Polarimetric Scattering Mechanism, PSM)间的最佳边界。具体的边界条件将在后文分类应用部分给出。
已确认的是,本方法仅对简缩极化中的双圆极化(Dual Circular Polarization, DCP或CC)模式有效。该模式要求雷达系统发射正交的圆极化波,并使用正交的圆极化基进行接收[10]。但是由于CTLR模式与CC模式间的散射矢量存在以下关系[91]:
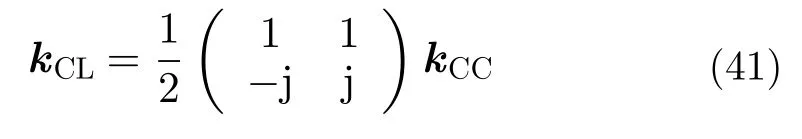
其中,kCL与kCC分别是CTLR与CC模式的散射矢量。因此针对CTLR模式得到的数据,可以先将其转化为CC模式数据,再应用本方法。
5.3.4 基于散射模型的方法通过著名的Freeman-Durden分解算法可以将全极化数据分解为3种基于物理散射模型的理想散射分量[92]:
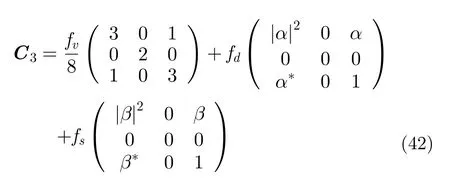
其中,fv,fd, 与fs分别代表体散射、2次散射与表面散射分量,|α|¸1代表2次散射分量HH与VV项之间的共轭,而|β|<1是表面散射分量HH与VV项之间的共轭。
类似地,协方差矩阵同样可以表示为这3种散射分量的和[93,94]:
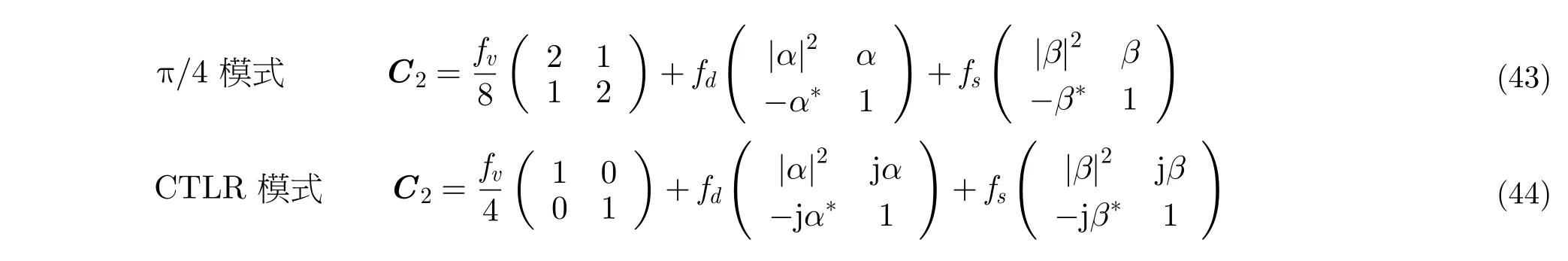
6 简缩极化应用
6.1 地物的非监督分类
雷达极化中最重要的应用之一是地物的分类与监测。简缩极化所带来的宽测绘幅宽优势可以提升星载极化SAR系统的这一能力。与此同时,这一项优势还可以降低星载极化SAR系统获取同一场景相干时序雷达图像所需的时间间隔。但是由于通过简缩极化获取的极化信息本就是非完备的,因此简缩极化数据处理的研究目标是在同一个后向散射分类策略下获得与全极化SAR类似的数据处理结果。
6.1.1 基于Stokes矢量的分类算法利用前文所述的m与δ参数,Charbonneau等人提出了利用三角函数将总功率(g0)分解成2次散射、体散射与表面散射的分解算法[12]。分解得到的各散射类的功率为:
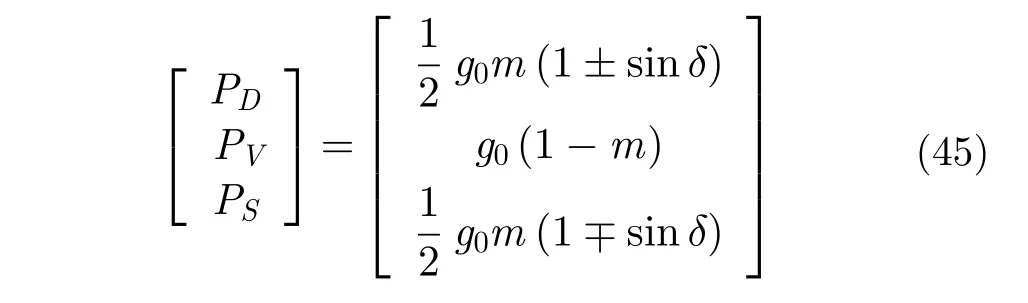
其中,D,V,S分别代表2次散射、体散射与表面散射,而式中的上下标与前文一致,对应不同的发射设置。通过式(45)得到的各PSM的功率不仅可以用来构成极化SAR图像的色彩基,还可以用来对图像中的像素作分类。需要注意的是,如用作色彩基,需使用幅度形式,即功率的开方。一种非常直接的分类方法是按照各像素中功率占优的PSM进行分类[36]。

类似地,各散射类的能量还可以通过基于m-χ或m-αs参数的分解算法得到:由于χ与αs参数的定义是对发射模式自适应的,因此公式(46)对CTLR模式的所有发射模式(左旋或右旋圆极化发射)均成立。
图8中展示了这些算法得到的分类结果。这里使用的数据是四视旧金山NASA/JPL AIRSAR L波段的全极化数据。对应的模拟左旋圆极化CTLR模式数据是通过欧空局(European Space Agency, ESA)PolSAR Pro 5.0软件转化得到的。由于数据本身已经是四视的,因此空间平均步骤仅使用了5×5矩形窗滤波器进行滤波。可以看到,两幅分类图近乎相同。而且所有分类图中,体散射类均明显被高估了。根据Cloude等人[63]的研究结果,这可能是简缩极化固有的特点。其原因在于简缩极化模式下,森林地区的散射熵会比全极化模式高。

图8 基于不同分解算法的分类图Fig. 8 Classification maps with different decomposition algorithms
6.1.2 简缩H-alpha分类算法另一类非监督分类方法是利用前述特征值分解算法(或简缩H/alpha分解算法)得到的简缩极化信息。文献[40]中建议不同PSM间的最佳边界值为:
低熵与中熵区域间的边界值为H=0.65,而中熵与高熵区域间的边界值为H=0.96。
在低熵区域内,多次散射类与偶极子散射类间的边界值为α=42°,而偶极子散射类与表面散射类间的边界值为α=48°。
在中熵区域内,多次散射类与植被散射类间的边界值大约为α=40°,而植被散射类与表面散射类间的边界值为α=51°。
在高熵区域内,几乎所有PSM均为植被散射类。多次散射类与植被散射类间的边界值为α=34.5°,而植被散射类与表面散射类间的边界值为α=51°。
图9中展示的是对前文使用的数据的分类结果。
6.1.3 基于Wishart分类器的分类算法由于不可缺少的空间平均步骤,前两小节得到的分类结果均难以保证图像的细节与纹理特征。为了提升分类结果,需要进一步利用CTLR模式数据的统计特性。与全极化SAR的散射矢量相同,CTLR模式的散射矢量服从复高斯分布[39]。因此,同样可以在CTLR模式数据中应用Wishart分类器。
文献[33,39]与文献[38]结合了Wishart分类器与简缩极化H/alpha分解算法和基于Stokes参数的分解算法。图10中展示的是利用Zhang等人[40]建议的H/alpha平面边界值得到的分类结果。可以看到,引入了Wishart分类器后,图像的细节与纹理特征均较好地得以保留。
对于第2种分类方法,我们增加了两步提纯步骤,即排除没有明确PSM的像素与利用总功率(span)的聚类步骤,以保证初始Wishart类的可靠性[38]。分类结果如图11所示。
6.2 简缩极化干涉SAR
简缩极化干涉SAR技术是目前简缩极化领域的一个研究热点。简缩极化干涉SAR系统通过一次单基线干涉或者重轨干涉可以获得目标场景中每个分辨单元的2个目标散射矢量。基线两端获得的简缩极化目标散射矢量分别用表示。通过将2个目标散射矢量顺序组合,可以获得一个4维的复散射矢量,因此简缩极化干涉SAR的极化与干涉信息可以用一个4×4矩阵表示:

图9 缩极化H/alpha分类结果Fig. 9 CompactH/alpha classification results
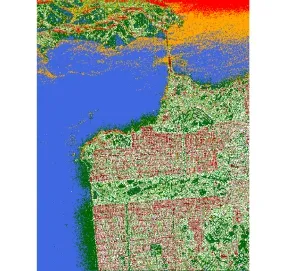
图10 简缩H/alpha/Wishart分类算法的分类结果Fig. 10 The classification maps of the compactH/alpha/Wishart algorithm with the same color labels as in Fig. 9(a).
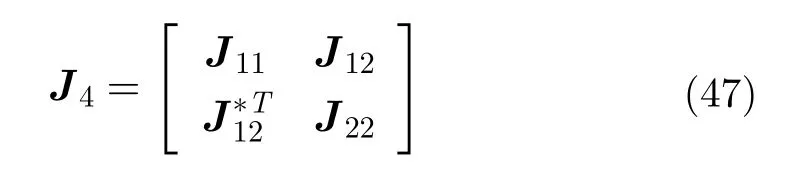
其中,矩阵J11和J22是基线两端的简缩极化自相关矩阵,J12是干涉互相关矩阵。
简缩极化干涉SAR数据处理方法主要有两种,一是将简缩极化干涉SAR数据重建成伪全极化干涉SAR数据[24,25],重建思想与第5.3.1节相似,一旦重建得到伪全极化干涉SAR数据,传统的全极化干涉SAR数据处理方法都可以使用;另外一个非常重要也是经典的数据处理方法是,不进行信息重建,直接对简缩极化干涉SAR数据进行处理。本节仅回顾了第2种数据处理方法中两个经典的简缩极化干涉SAR应用。

图11 m/chi/Wishart分类算法的分类结果Fig. 11 Classification results of the m/chi/Wishart algorithm
6.2.1 森林树高反演树高反演是简缩极化干涉SAR技术的一个典型的应用。大多数的树高反演方法都是基于RVoG模型的。该模型是一种能够表征不同极化状态的复干涉相干系数随垂直结构参数变化规律的二层结构模型。这二层包括一个地表层和一个均匀体散射层。树高反演过程包括:根据相干系数拟合直线、根据拟合直线与单位圆的交点计算地表相位、计算代表树高信息的体散射去相干等。树高反演过程中,最重要的步骤便是直线的拟合及体散射去相干的正确估计。无论哪种树反演方法,都是基于简缩极化干涉SAR的复相干系数做处理。复相干系数为:
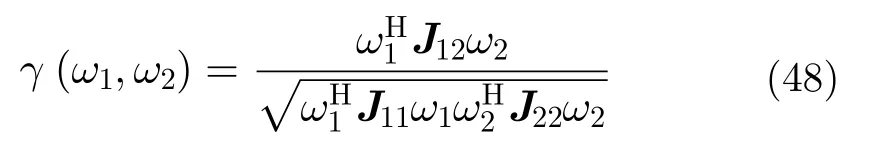
其中,ω1与ω2代表基线两端接收极化状态。
在参考文献[21,22]中,是通过求得接收天线在所有极化状态下的复相干来计算简缩极化干涉复相干的轨迹。基于求得的复相干轨迹拟合出一条直线,然后再运用三阶段反演方法进行树高估计。详细步骤如下:
(1) 变换接收天线的极化状态(式(48)中ω1,ω2),计算不同极化状态下的复相干,并根据复相干分布拟合直线。
(2) 计算拟合直线与单位圆的两个交点,正确选择其中一个表示地表相位的交点。
(3) 选择距离地表相位最远的复相干系数表示树高的体散射相干系数去掉地表相位影响并求得仅由体散射引起的复相干γv。
(4) 应用查表法(Look-Up Table, LUT)技术最终求得森林的树高以及森林消光系数。
参考文献[26]中的树高反演方法不同于参考文献[21,22]。在文献[26]中,不计算简缩极化干涉复相干轨迹,而是通过计算几个复相干进行直线拟合,用于直线拟合的复相干包括:两个接收通道的各自复相干,无约束最优相干和最大相位分离复相干。最大相位分离复相干用于估计地表相位及初步估计体散射去相干,然后通过计算简缩极化干涉相干区域的边界来修正体散射去相干,获得了精确的地表相位及体散射去相干后,采用查表法进行树高及消光系数的估计。
6.2.2 简缩极化干涉SAR目标分解参考文献[28]与文献[30]提出了基于简缩极化干涉SAR数据的目标分解方法。该方法将全极化中 Freeman-Durden三分量目标分解方法应用到简缩极化干涉SAR数据中[25]。类似于5.3.4节的内容,该方法将简缩极化干涉SAR的协方差矩阵J2分解为对应表面散射、2次散射与体散射的3个矩阵之和。

注意,这里的fcv,fcs,fcd均为包含功率与相位中心高度信息的复系数。
该算法的验证使用的是由PolSARProSim软件生成的仿真数据。根据10 m的森林树高,生成了仿真L波段全极化干涉SAR数据。仿真场景的Pauli图如图12(a)所示。途中红线代表下文分析所取的一条方位线数据。将仿真的全极化SAR数据转换成简缩极化SAR数据,获得简缩极化干涉互相关矩阵J2。分解结果如图12(c)所示。图中Odd, DBL与VOL分别代表奇次散射类、2次散射类与体散射类,VC与HC分别表示发射圆极化并使用V或H线性极化接收。通过对简缩极化干涉SAR数据进行目标分解,各散射机制的功率信息及散射相位中心高度信息都能被获得,此外该目标分解结果与全极化干涉目标分解结果[95]非常吻合,这也验证了简缩极化干涉SAR在目标分解方面的应用潜能。
6.3 其他应用
除了前文介绍的这两类主要简缩极化应用以外,还有一些受益于宽测绘幅宽优势的简缩极化应用,包括土壤湿度估计[17-20],冰山[43-45]、溢油[46-53]与船舶检测[42,45,52-55],农作物分类[56-61]与海冰监测[12-14,85,86]等。调研结果表明,可以在这些应用领域内通过简缩极化数据得到与全极化数据性能相似的数据处理结果。
7 结束语
本文全面地回顾了基于混合极化架构的极化SAR的原理与应用。混合极化架构实际上首先是一种强调使用两路信号通道合成发射极化波的极化SAR系统设计方案。雷达系统理论上可以产生任意极化波,包括简缩极化所需的圆极化波与斜线性极化波(即±45°极化波)。也就是说,这一特性使得基于混合极化架构的极化SAR系统可以工作在不同的简缩极化模式下。而简缩极化模式相比传统线性双极化模式,可以得到更好的分类结果。另外,如果最终采用的发射极化波拥有相等的H与V分量,则极化SAR系统可以额外拥有独特的自我检测标定特性。这一系统设计方案还强调接收极化基需与发射极化不同。这样,极化SAR系统的距离模糊问题可以得到改善,进而进一步增加雷达系统在全极化模式下的测绘幅宽大小。这一系统设计方案所需求的射频器件也较少,因而能够保证保证系统的成本更低、鲁棒性更好。最后,得益于更宽的测绘幅宽,基于混合极化架构的极化SAR系统可以在更短的时间间隔内获取同一目标场景的相干雷达图像。
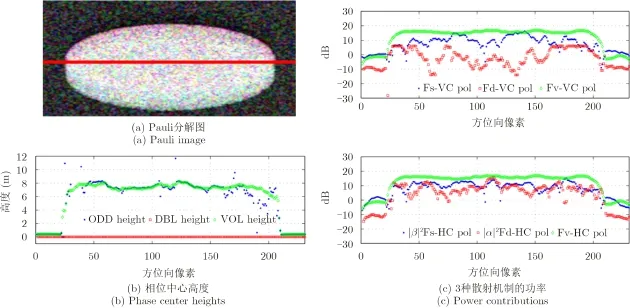
图12 仿真数据的Pauli分解图Fig. 12 Simulated dataset Pauli decomposition image
本文同时指出了混合极化架构在工程实现中的难点,即工作在双极化模式时,发射失真无法被标定。另外,混合极化架构所采用的发射极化总是圆极化的。但是在某些应用中,使用其他极化波进行发射能够得到更好的结果。为了克服这些难点,本文提出了一个混合极化架构的改进版本。在改进型混合极化架构下,可以应用预失真技术修正发射失真。相比拥有额外内定标回路的雷达系统,本文提出的改进型混合极化架构需要的射频器件更少。另外,基于改进型混合极化架构的极化SAR系统可以发射任意极化波,从而可以进一步支持π/4模式以及使用其他互相正交的发射极化基的全极化模式。本文最后展示了基于此改进型混合极化架构的原型系统。原型系统的相关实验验证与测试工作仍在进行中。
致谢对混合极化架构研究项目作出重要贡献的有:洪文教授组织规划了整个项目;李洋博士、张晶晶参与了最初的系统设计工作;陈琳博士、张晶晶参与了简缩极化定标算法的设计工作;陈琳博士、郭胜龙博士与陈诗强参与了简缩极化应用研究工作;陈诗强、郭胜龙博士与尹嫱博士参与改进型混合极化架构原型机的集成及后续实验验证工作。
TN958
A
2095-283X(2016)06-0559-37
10.12000/JR16074
洪文. 基于混合极化架构的极化SAR:原理与应用[J]. 雷达学报, 2016, 5(6): 559-595.
10.12000/JR16074.
Reference format:Hong Wen. Hybrid-polarity architecture based polarimetric SAR: Principles and applications[J]. Journal of Radars, 2016, 5(6): 559-595. DOI: 10.12000/JR16074.
2016-05-17;改回日期:2016-08-12;
2016-09-26
*通信作者: 洪文 whong@mail.ie.ac.cn
国家自然科学基金(61431018)
Foundation Item: The National Natural Science Foundation of China (61431018)

