铜精矿的聚类分析及判别分析

李绍平， 李 云， 杨 鸿

(云南锡业股份有限公司铜业分公司， 云南 个旧 661000)

铜精矿的聚类分析及判别分析

李绍平， 李 云， 杨 鸿

(云南锡业股份有限公司铜业分公司， 云南 个旧 661000)

应用聚类分析的方法对现有的铜精矿进行归类，在此基础上对新的铜精矿根据品位判别其归属哪一类，有助于原料配矿，为原料管理提供一些建设性的思路、方法和结果。

铜精矿； 聚类分析； 判别分析

0 引言

聚类分析是一种重要的多变量统计方法，其分类的基本原则是依据事物性质比较相似，或者说它们之间的距离比较小(这里的距离指欧氏距离平方、绝对距离等)归为一类。铜精矿合理的分类对于生产统计和投配料有着重要意义，即通过反复实践逐步得到一种较为标准的分类，形成标准化程序化的操作，从而提高生产效率和各项指标。

1 聚类分析

1.1 聚类方法

聚类就是把相似的事物聚在一起归为一类，在这里就是通过一些数学方法把相似的事物聚在一起。其原则是同一类中的个体相似性大，不同类中的个体差异很大。聚类分析在社会科学用统计软件包(以下简称软件包)分为快速聚类和分层聚类。

快速聚类的基本思想是，选择一批聚类中心，让样品按某种原则向中心凝聚，得出一个初始的分类，按照最近距离原则对中心进行不断地修改或迭代，直至分类比较合理稳定为止。类的个数k可以事先指定，也可以在聚类过程中确定。在软件包按Analyze—Classify—K-Means Cluster的顺序操作。

分层聚类的基本思想是,令n个样品自成一类，计算出相似性测度，此时类间距离与样品间距离是等价的，把测度最小的两个类合并；然后按照某种聚类方法计算类间的距离，再按最小距离准则并类；这样每次减少一类，持续下去直到所有样品都归为一类为止。

以下叙述的是分层聚类几种方法，在软件包按Analyze—Classify—Hierachical Classify的顺序操作，单击方法选择Method功能就有以下几种方法可选择：

组间连接——合并两类后的结果使所有对应两项之间的平均距离最小。

组内连接——若当两类合并为一类后，合并后类中的所有项之间的平均距离最小。

最近邻法——用两类之间最近点间的距离代表两类间的距离。

最远邻法——用两类之间最远点间的距离代表两类间的距离，也叫完全连接法。

重心聚类法——以计算所有各项均值间距离的方法计算两类间距离。该距离随着聚类打开进行不断减小。

中位数法——以各类中的中位数为类中心。

最小方差法——以类间方差最小为聚类原则。

在选定用什么方法后，还需对距离的测度选择：设有N个样本1，2，…n，每个样本有m项指标x1，x2，…，xm,用xij表示第i个样品第j个指标的值。

绝对距离(Block)：

欧氏距离(Eeclidean distance)：

车比雪夫距离(Chebychev)：

1.2 聚类实例

表1是各公司入厂铜精矿中Au、Ag、Cu、Zn、As的平均品位。

表1 铜精矿部分元素平均品位 %

表2采取两种分类方法，即快速聚类和分层聚类(组间连接)，根据杂质Au、Ag、Cu、Zn、As平均品位把各公司入厂铜精矿分为3类。

表2铜精矿分类表

铜精矿来源类别(快速聚类)类别(多层聚类组间连接)公司111公司232公司332公司432公司511公司632公司711公司832公司923公司1011公司1132公司1232公司1332公司1412公司1512公司1632公司1732公司1811公司1932公司2032公司2132公司2232公司2332公司2432公司2532公司2623公司2732公司2832公司2923公司3032公司3132

由表2可见，不同的分类方法得出不同的分类结果。统计包正好提供了若干分类方法，具体采用什么样的方法要根据需要选择(如，按不同的分类方法，观察以某一类进行配料，然后投入生产，产出后，看某一类直收情况，经多次试验，可能会找出直收较高的一类)。

2 判别分析

2.1 判别方法

判别分析(Discriminant Analysis，DA)是费舍(R. A. Fisher)于1936年提出的。基本原理是从已知的各种分类情况中总结规律求出判别函数，对要判别的样本，判断其与判别函数之间的概率、距离、离差等最有可能的参数对未知所属类别的事物进行分类的一种分析方法。常用判别方法：最大似然法、距离判别法、Fisher判别法、Bayes判别法及逐步判别法等。这里就一两种方法进行推导，以便在判别分析时做到胸有成竹。

再计算联合组内协方差矩阵

上式中x的系数即为分类函数系数，见表3。

表3分类函数系数

LB123Au2.1561.4331.788Ag0.1470.0530.307Cu1.5301.4451.683Zn2.0200.7911.372As6.48912.109-8.550(Constant)-43.660-22.862-103.465

下面是典型判别函数系数的计算。

第一步，计算W：

第二步，计算B：

第三步解特征方程：

|W-1B-λI|=0

求出特征根λ,再解含有未知数ai的方程：

(W-1B-λiI)ai=0,i=1,2,

ai还要满足：

a′iSai=1

解出的ai就是点则判别函数的系数，常数项的计算公式为：

典型判别函数系数见表4。

表4典型判别函数系数

Function12Ag0.024-0.002As-1.9733.403(Constant)-3.248-0.826

2.2 判别实例

根据分类函数系数列出判别式如下：

F1=2.156Au+0.147Ag+1.530Cu+2.020Zn+6.4890As-43.660

F2=1.433Au+0.053Ag+1.445Cu+0.791Zn+12.109As-22.862

F3=1.788Au+0.307Ag+1.683Cu+1.372Zn-8.550As-103.4650

如果要判别云南华联锌铟股份有限公司200TK150245批精矿属于哪一类，只要把Au、Ag、Cu、Zn、As的品位0.6、459.8、26.1、2.77、0.657代入以上三式，计算得75.016、50.228、80.876，通过比较， 3个值中最大的对应的类别，就是它所属的类别。显然80.876是最大值，对应的归为第三类。

亦可利用表4典型判别函数系数进行判别分类，可利用公式

Y1=0.024Ag-1.9730As-3.248

Y2=-0.002Ag+3.403As-0.826

计算得Y1=6.49，Y2=0.49，对照图1领域图，看其在哪个领域，就属于哪类。对照结果归属第三类。从散点图2可看出这三类有明显的区别。

图1 领域图

3 结束语

聚类方法的选择需要反复试验确定最优效果，但不同方法的结果差别不应很大，否则说明聚类变量的选择没能真正反映观测量的分类特征。原料是铜冶炼的物质基础，做好原料的分类配比以及原料标准化，是改善各项技术经济指标、提高经济效益的一个重要途径。根据原料的各元素品位，合理地分类和搭配，可达到低投入，高产出的目的，即提高直收率。 以上分析应达到两个目的，一是提供一些分析结果；二是提供一些方法，旨在实践中反复观察总结推广运用。

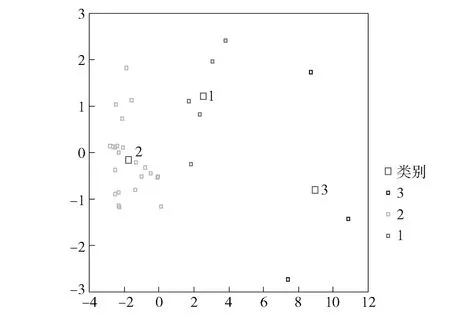
图2 散点图

[1] 朱一力.统计分析软件从入门到精通[M].北京：电子工业出版社,1997.6.

[2] 周复恭.应用数理统计[M].北京：中国广播电视大学出版社,1987.6.

[3] 黄海.SPSSFORWINDOWS统计分析[M].北京：人民邮电出版社,2001.2.

铜绿山古矿业遗址炉渣含铜量0.49%

湖北省文物考古研究所联手北京高校，采用现代科学技术对大冶铜绿山四方塘遗址出土铜炉渣进行成分检测，最新披露的检测结论表明，距今2 600多年的春秋时期，铜绿山地区青铜冶炼技术，已处于古代世界领先水平。

铜绿山古矿业遗址是中国著名的古铜矿冶遗址，是中国青铜文化发祥地之一。2015年，根据国家文物局相关批复，湖北省文物考古研究所联合有关单位在铜绿山四方塘遗址进行多学科合作的发掘、研究和保护。为弄清楚当地古人的青铜冶炼技术，北京科技大学冶金与材料史研究所对遗址出土的20块炉渣进行抽样检测分析，得出的结论是，炉渣含铜量平均为0.49%。炉渣含铜量是青铜冶炼技术的重要指标，其数据越小，说明矿石中的铜在冶炼炉中还原得越充分，也就是说，对矿石的提炼水平越高。0.49%的数据，表明铜绿山地区炼铜技术在春秋时期已接近现代水平。

北京科技大学博士生导师李延祥教授，通过与希腊青铜时代、阿曼青铜时代、美国亚利桑那近代氧化矿石炼铜渣含铜量进行对比，发现铜绿山的数据最小。铜绿山地区青铜冶炼技术，处于古代世界领先水平。

Clustering analysis and discriminant analysis of copper concentrate

LI Shao-ping， LI Yun， YANG Hong

This paper classifies the available copper concentrates by clustering analysis, and differentiates category of new copper concentrate basis on per copper grade, it is favorable for raw material blending and can provide constructive ideas and methods for raw material management.

copper concentrates; clustering analysis; discriminant analysis

李绍平(1963—)，男，云南人，工程师，主要从事有色冶金统计工作。

2015-12-25

TF811

B

1672-6103(2016)02-0072-04