二维康托尔集上的多分辨分析

聂伟平， 师东利， 李万社

(陕西师范大学 数学与信息科学学院,西安 710062)

二维康托尔集上的多分辨分析

聂伟平， 师东利， 李万社

(陕西师范大学 数学与信息科学学院,西安 710062)

根据康托尔集构造了一个二维康托尔集,建立了二维康托尔集与L2(R2)空间的对应关系,给予多分辨分析的几何特征,用二维康托尔集建立了函数的尺度分析.

康托尔集；多分辨分析；基函数

1807年,法国数学、物理学家傅里叶(Jean Bap-tistle Joseph Fourier),提出任意一个周期为T=2π的函数f(t)都可以用三角级数表示.傅里叶变换的理论是人类数学发展史上的一个里程碑.从1807年开始,直到1966年,整整用了一个半世纪多,才发展成熟.她在各个领域产生了深刻的影响，得到了广泛的应用,推动了人类文明的发展.但是傅里叶也有很多缺陷，比如实际应用中的非平稳信号，傅里叶变换无法解决.小波变换与Fourier变换，Gabor变换相比，它是一个时间和频域的局域变换，因而能有效的从信号中提取出信息，通过伸缩或平移对函数或信号进行多尺度分析.小波变换的基函数ψa,b(t)不是唯一的，满足一定条件的函数均可以作为小波基函数，因此怎么找到完美的小波基函数是小波变换中非常重要的问题.Mallat和Meyer建立的多分辨分析为小波构造基函数提供了方法.本文对多分辨分析给出了一个简单的几何结构，丰富了多分辨分析的内涵，方便读者更好地理解多分辨分析.

1 预备知识

由一维多分辨分析[1]的定义可得，在一维空间中下列条件成立

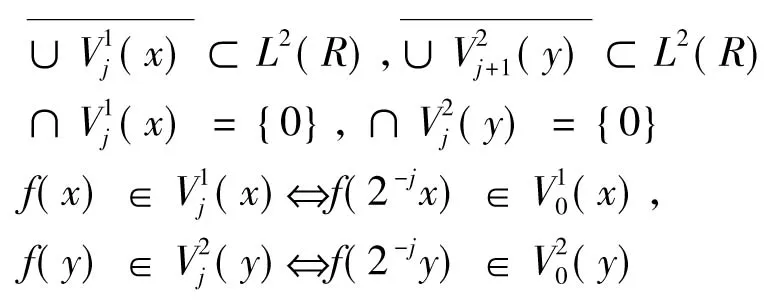
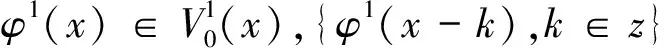
定义1[1]在L2(R2)函数空间的一串子空间序列集合{Vj,j∈z}称为依尺度函数φ(x,y)的多分辨分析，如果它满足以下5个条件：

(3)独立性：∩Vj(x,y)={0}.

(4)缩放性：f(x,y)∈Vj(x,y)⟺f(2-jx,2-jy)∈V0(x,y).

(5)规范正交基：φ1(x)φ2(y)∈V0(x,y),{φ1(x-k)φ2(y-j),k,j∈z}是V0(x,y)一组标准正交基.

由多分辨分析可以得到两个结果

Vj+1=Vj⊕Wj，

(1)

L2(R2)=VN(x,y)⊕Wj(x,y).

(2)

定义2[2]记E0=[0,1]，第一步(n=1),去掉中间的1/3,得E1=[0,1/3]∪[2/3,1].第二步(n=2),重复刚才的步骤,得E2=[0,1/9]∪[2/9,1/3]∪[2/3,7/9]∪[8/9,1],如此重复刚才的一系列步骤,得Ek,当k→时,遂得cantor集,记作).如图1所示.

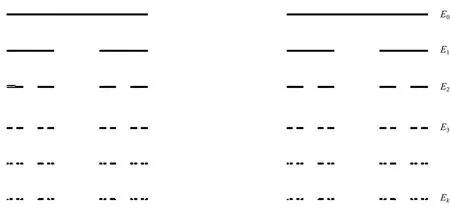
图1 康托尔三分集

2 二维康托尔集上的多分辨分析

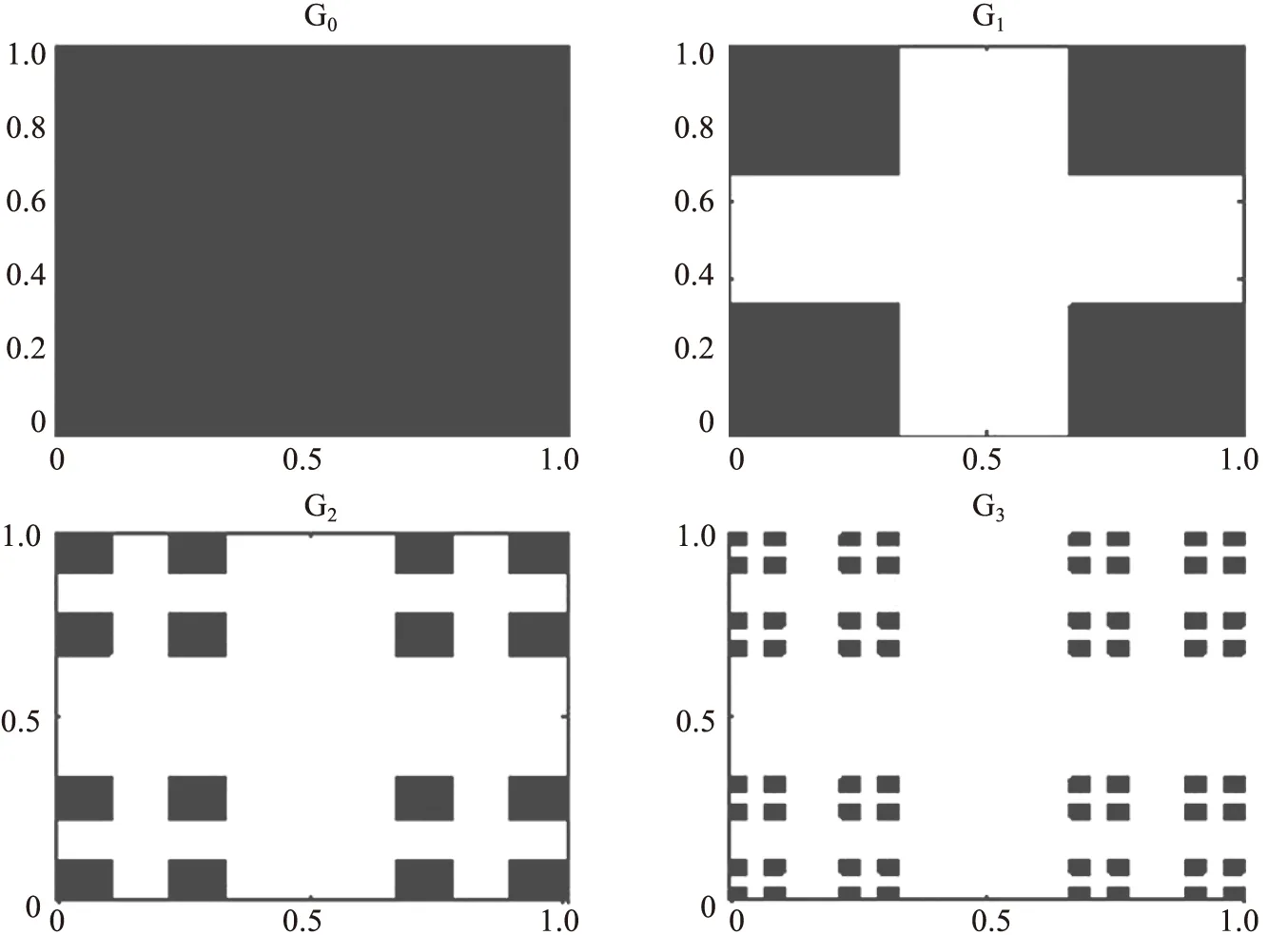
图2 二维康托尔集

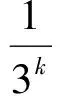
被截断的区域Nk=Fk×Fk,任意两个不同的区域的交集是空集,说明它们的特征函数(该区域的元素集合)CV(x)与CW(x)彼此正交，为了方便讨论，记CV(x):=V,CW(x):=W,则有V1∩W1={0},V2∩W2∩W1={0},…,VN∩W1∩W2∩…∩WN={0}.

图3 二维康托尔集上的多分辨分析

二维康托尔集与L2(R2)函数空间可以建立对应关系,因此L2(R2)空间中的子空间V0表示二维康托尔集的G0,每次去掉的部分子空间记为Wk,而每次剩余的部分记为Vk.很明显Wj∩Wk=Φ,意味着它们彼此正交(对于二维康托尔集而言,显然是它们的特征函数CWi与CWk彼此正交,以下解释相同),而Vi与Vj并不是正交的,V0可以分解为V1与W1的直和,即V0=V1⊕W1,W1就是V1在V0中的正交补空间,继续分割下去就有V0=V1⊕W1=V2⊕W2⊕W1=…,由此可知W1就是V0的空间结构的细节补充,在W空间上定义小波函数ψ(t),同时Vk就是在尺度k之下,φi(x,y)在Vk上的平移是正交的,但是不同尺度之间φi(x,y)与φj(x,y)并不正交.显然,单凭空间W1不能恢复W0,因为W1只是V1的补空间,因此只有将空间Vk与空间Wk结合起来,既在空间Vk用基函数φm,n(x,y),又在空间Wk用基函数ψm,n(x,y)同时展开f(x,y),这相当于L2(R2)空间的正交分解

(3)

对应的函数或信号f(x,y)的分解过程可表示为

f0(x,y)=f1(x,y)+d1(x,y)=f2(x,y)+d2(x,y)+d1(x,y)=

f3(x,y)+d3(x,y)+d2(x,y)+d1(x,y)=…=

(4)

很明显式(1)、(2)、(3)、(4)是完全等价的，这样我们把二维康托尔集和L2(R2)空间建立了对应关系，对L2(R2)空间赋予多分辨分析的几何特征，这是多分辨分析从抽象的数学定义转变为使用信号的关键步骤，对L2(R2)空间的正交分解和不断变换尺度空间来逼近一个函数或者信号的基本过程和问题的实质，也对Mallat和Meyer创立的多分辨分析的基本思想所做的物理、几何和集合论的解释[3]，说明二维康托尔集建立的多尺度分析比多分辨分析的结构更加直观，几何结构更加清晰.

[1] 关履泰.小波方法与应用[M].北京：高等教育出版社，2007.

[2] 李水根，吴纪桃.分形与小波[M].北京：科学出版社，2002.

[3] 熊小云.函数在Cantor集上的多分辨分析[J].自然科学进展,1998,8(2):247-250.

[4] XIA X G,GERONIMO J S,HARDIN D P，et al.Design of prefilters for diserete multi-wavelet transforms[J].IEEE.Trans.on SP.,1996,1(1):25-35.

[5] FENG D J,HUA S,WEN Z Y.The pointwise densities of the Cantor measUre1[J].Journal of Mathematical Analysis and Applications,2000,250:692-705.

[6] SHER R B.Concerning wild Cantor sets in E3[J].Proc.Amer.Math.Soc., 1968，19:1195-1200.

[7] MATJA E.On defining seqUences for Cantor sets[J].Topology and its Applications，2001，113：321-325.

[8] CHRISTENSEN E,IVAN C.Spectral triples for AF C*-algebras and metrics on the Cantor set[J].J.Operator Theory，2006，56：17-46.

[9] ELJKO M.On defining seqUences for Cantor sets[J].Topology and its Applications，2001，113：321-325.

[10]MALLAT S.A theory of multiresolution signal decomposition:The wavelet transform[J].IEEE Trans,1989，11(7)：674-693.

[11]MALLAT S.Multiresolution approximation and wavelet orthonormal bases of L2[J].Trans.Amer.Math.Soc.,1989，315：69-87.

[责任编辑 王新奇]

The Multi Resolution Analysis of Two-dimensional Cantor Set

NIE Wei-ping, SHI Dong-li, LI Wan-she

(School of Mathematics and Information Science, Shaanxi Normal University, Xi’an 710062, China)

According to the Cantor set, the two-dimensional Cantor set is built. The corresponding relationship between two-dimensional Cantor set andL2(R2) space is set up. The geometrical characteristics of multi resolution analysis is presented. The scale analysis of function is established by the two-dimensional Cantor set.

Cantor set; multi resolution analysis; basis function

1008-5564(2016)05-0026-04

2016-03-08

聂伟平(1990—),女，河南许昌人，陕西师范大学数学与信息科学学院硕士研究生，主要从事智能信号处理研究.

O189.12；O24.16

A