一类考虑反S型概率权重的供货中断库存模型①

陈俊霖, 赵晓波, 王小劼

( 1． 中央财经大学管理科学与工程学院, 北京 100081; 2． 清华大学工业工程系, 北京 100084)



一类考虑反S型概率权重的供货中断库存模型①

陈俊霖1, 赵晓波2, 王小劼2

( 1． 中央财经大学管理科学与工程学院, 北京 100081; 2． 清华大学工业工程系, 北京 100084)

在连续盘点库存系统中应用零点订货库存(ZIO)策略,假设供应商工作和中断的持续时间分别服从独立的指数分布.首先,引入反S型权重函数刻画风险厌恶型决策者主观高估补货点供应商处于中断的小概率关键事件的行为偏好.其次,利用两个状态连续时间Markov链和更新报酬定理构建了长程平均成本模型,证明了成本函数的单峰性, 对比讨论了结合数值算例与风险中性模型结论.最后,设计了近似条件得出最优订货量的解析表达式及成本的近似误差上界,配合基准集和随机数据集分别计算了160组和10 000组数值实验样本,验证了近似方法的有效性.

供货风险; 风险厌恶; 反S型权重; 库存

0 引 言

行为运作管理作为新兴学科近年来已成为学术界关注的焦点[13]. 一些学者将决策者的风险态度引入经典的库存模型, 并论证修正的库存模型可更好地指导决策. Merzifonluoglu[14]采用均值-方差效用函数构建了风险厌恶偏好下的报童模型，并分析了它对最优订货量的影响. Giri[15]采用指数效用函数刻画零售商的风险态度, 在双渠道单期库存系统中分析零售商的最优常规订货量和最优应急预定量. Chen等[16]基于周期性盘点库存系统, 刻画了指数效用函数下最优库存(定价)结构策略. 简惠云和许民利[17]通过设计实验室实验论证了零售商具有显著的风险规避或风险寻求特征, 风险态度可用CVaR效用函数进行刻画. 代建生等[18]分析了销售商的风险规避偏好对回购契约实施的影响. 王丽梅等[19]采用均值-方差效用函数分析现货供应不确定条件下, 风险厌恶型的销售商的库存优化策略. 于辉等[20]建立了CVaR下的供应商-零售商收益共享契约以分析供应链应急恢复优化策略. 以上均为从量级(magnitude)的角度构建引入风险态度的库存管理模型.

另一方面, 风险发生的概率(probability)也是随机中断环境的关键要素. 如Ellis等[21]在调查了223名买方后所指出, 供货中断风险的量级与发生概率均为买方衡量卖方总体可靠性的两个重要方面. Kahneman和Tversky[22]的研究表明决策者的风险态度在发生概率上亦有明显的表现. 损失发生的小概率事件通常被主观高估, 大概率事件被主观低估, 因此权重函数曲线呈现反S型的特点(图1). 从风险发生概率的角度研究风险态度下的库存管理问题并不多见. Ranjan和Shogren[23]发现主观放大的损失概率将导致水资源供给大打折扣. 陈俊霖和赵晓波[24]指在供需双方或一方具有反S权重风险态度时, 批发价格合同可使供应链在双方均有激励动机下达到协调. Chen等[25]通过仿真实验讨论了反S权重函数在连续盘点库存系统中的应用.

本文基于随机供货中断环境下的连续盘点库存系统, 考察在补货点发生供货中断的小概率关键事件对最优定货决策以及库存系统运行的影响. 本文采用Prelec[26]反S型权重函数刻画决策者风险厌恶偏好, 构建零点订货库存策略下的成本优化模型, 证明了最优订货决策的惟一性并提出了其近似解析解. 通过与风险中性模型进行对比分析, 描述了风险厌恶行为偏好下系统最优订货量以及成本的偏差情况.

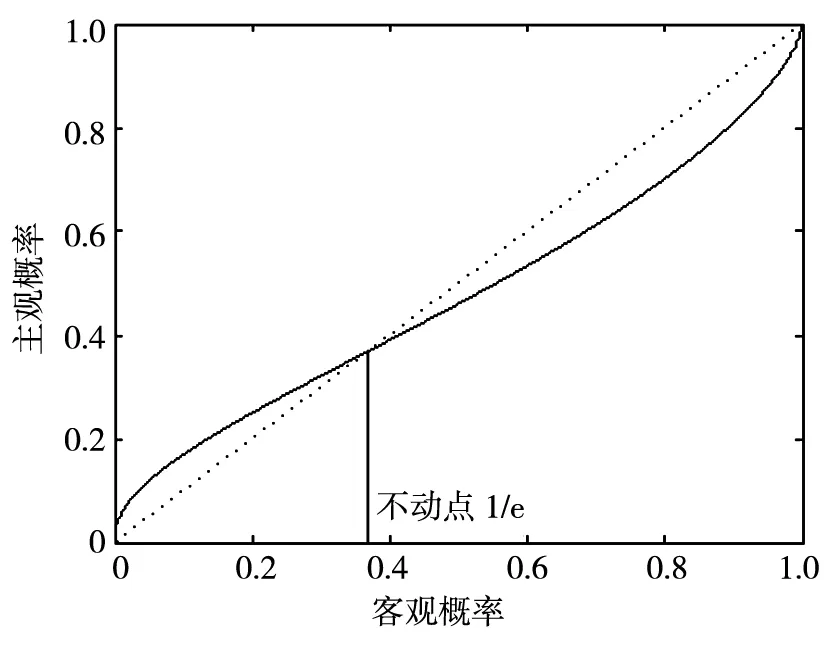
图1 反S型权重函数示意图

1 模型构建与分析

考虑一个连续盘点库存系统. 生产商从供应商处订货并供给需求客户. 供应商面临供货中断风险, 其正常工作(状态0)和供货中断(状态1)的持续时间分别服从参数为λ和μ的指数分布. 以Xi为第i-1次中断结束后直到第i次中断发生时, 供应商已持续工作的时间, 则Xi的密度函数为f1(xi)=λe-λxi; 以Si为第i次中断持续的时间, 则Si的密度函数为f0(si)=μe-μsi. 采用两状态连续时间马尔科夫链描述供应商的状态转移过程. 设βij(t)为供应商从状态i经过时间t(≥0)后转移到状态j的概率,i,j=0或1, 则根据Kolmogorov Forward 等式[27], 有

(1)

(2)

设生产商单次订货成本为K,单位产品单位时间的持货成本为h. 当系统库存水平不为0时, 按速率D满足用户需求, 一旦库存水平降到0, 生产商则订取批量为Q的产品. 若供应商处于工作状态, 货物瞬时到达,提前期为0; 若供应商处于中断状态, 则订单要待供应商处于工作状态时才可完成, 在此等待期间, 未满足的用户每单位产品需求损失成本为π. 据上述描述可知, 生产商库存的变化过程是随订货重复进行的, 将库存到达Q的两次相邻订货期视为1个周期, 用T表示.图2描述了供应商的状态和库存水平随时间变化的样本过程.

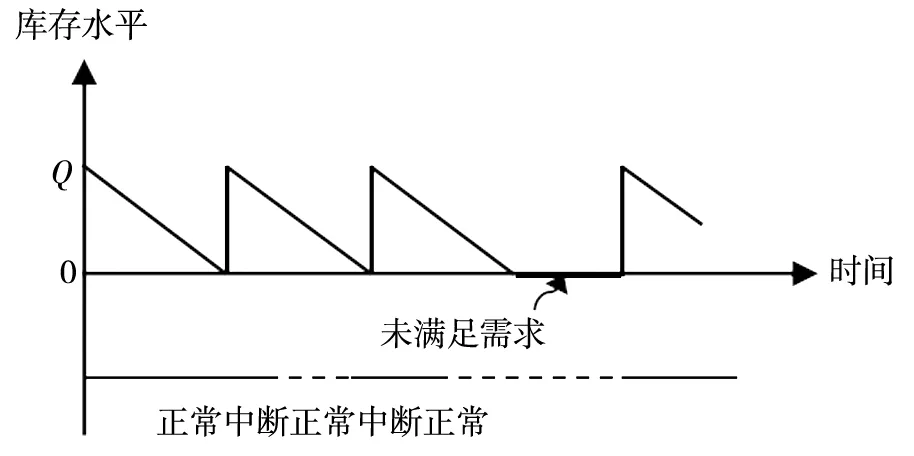
图2 供应商状态和库存水平随时间变化示意图

在1个周期内, 库存水平从期初(t=0)Q逐渐以D速率下降, 在时刻点t=Q/D到达0点. 根据周期的定义,期初t=0供应商均为正常工作状态, 当t=Q/D时, 供应商无法供货的概率为β01(t=Q/D). 因供应商工作和中断时间服从独立的指数分布, 故单个周期长度T的概率密度函数[5-6]为

(3)

通常, 供应商发生中断为小概率事件, 供应商正常工作持续的时间比其供货中断的时间更长, 因此可假设λ<μ, 并且, 可假设订货时刻点供应商无法供货概率β01(t=Q/D)<1/e. 这里, 1/e为Prelec[26]提出的单参数概率权重函数不动点. 如图1所示, 风险厌恶型决策者主观高估小于1/e的小概率损失，对于大于1/e的大概率事件则主观低估. 由于本文讨论风险厌恶型决策者对订货时刻点供应商无法供货的小概率主观放大的行为,因此仅考虑β01≤1/e的部分. Prelec[26]单参数权重函数形式为

w01(β01)=e-(-lnβ01)γ, 0<γ≤1

(4)

式中参数γ描述决策者风险厌恶程度,γ越大, 风险厌恶程度越低,γ=1表示决策者风险中性,即w01=β01.

根据等级依赖效用理论(rank-dependent expected utility theory)[28], 可得风险厌恶型决策者的主观概率为

w01(Q/D)=e-(-lnβ01(Q/D))γ

(5)

w00(Q/D)=1-e-(-lnβ01(Q/D))γ

(6)

以下为了简化表述,将β01(Q/D),w01(Q/D)分别简称为β0(Q),w0(Q).

以E(C)表示1个周期内生产商发生的库存总成本期望的主观效用值, 包括1次订货成本K、库存持货成本hQ2/(2D)、以及可能发生缺货成本πDw0(Q)/μ, 因此

1个周期T期望时间为总的工作时间加等待时间的期望. 总的工作时间为Q/D, 等待时间期望可由单个周期长度T的概率密度函数加权平均求得. 由式(3)知,周期长度T的概率密度函数依赖于决策者对t=Q/D时刻供应商无法供货的概率判断, 因此, 引入主观周期长度T′,易得T′的概率密度函数为

(7)

据此, 周期长度T′期望值E(T′)=Q/D+w0(Q)/μ. 根据更新报酬定理可知, 系统长期运行平均成本等于单个周期的期望成本与单个周期期望时间长度之比. 令gs为系统长期运行平均成本函数, 则

(8)

考虑极端的情况. 若供应商十分可靠, 参数λ<<μ, 或λ/μ→0; 此时式(8)中成本函数gs(Q),收敛为经典的EOQ成本函数, 记为gE(Q), 如命题1所示.

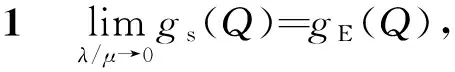
证明略.

命题2 在β0(Q)∈[0,1/e条件下,w0(Q)是关于Q(>0)的增凹函数; 给定Q(>0), 以参数γ(0<γ≤1)为变量, 则w0是关于γ(0<γ≤1)的减函数.

命题3 在Q>0,gE(Q)<πD的条件下,gs(Q)是关于w0(Q)的增函数; 给定Q(>0), 以参数γ(0<γ≤1)为变量,则gs是关于γ(0<γ≤1)的减函数.

参数γ描述决策者风险厌恶程度,γ越大, 风险厌恶程度越低. 因此, 由命题2, 命题3可知, 在同等订货量Q(>0)的条件下,风险厌恶程度越高(γ越小)的决策者认为订货时刻点供应商无法供货的概率w0(Q)越大, 从而感知的成本gs(Q)越高. 这一结论是符合直观的.

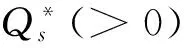
2 模型近似

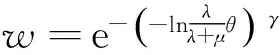
令g(Q)表示近似条件下的系统长期运行平均成本函数, 则

(9)

在近似条件下, 系统的最优订货量以及系统最小成本如命题5所示.

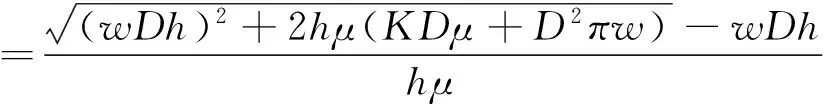
近似成本函数g(Q)的凸性为求取最优订货量Q*的解析表达式提供了便利.化简Q*可得

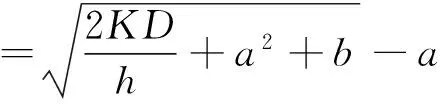
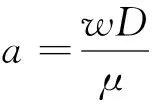
近似方法可以在一定程度上提供满意的优化决策, 其近似解的精确性对决策效果的影响也是不容忽视的. 进一步探讨最优订货量以及系统成本的近似误差.采用近似成本函数与原成本函数之差, 除以原成本函数归一化得到近似误差比值. 通过近似误差比值分析成本函数近似的精确程度, 分析结论如命题6所示.

(b)在Q>0,gs(Q)<πD的条件下, 有

g(Q)≥gs(Q);

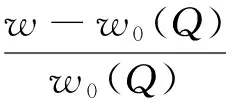
3 数值分析

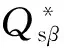
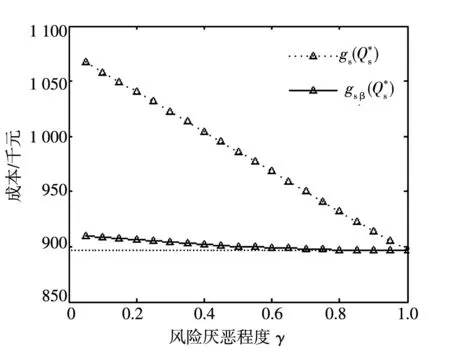
图关于γ的变化趋势

参数1/λ表示1个周期内供应商正常供货期望时间,μ/λ表示1个周期内正常供货期望时间与供货中断期望时间的比值. 可以认为, 较大的λ表示供应商更易发生中断; 在给定λ的条件下, 较大的μ/λ表示供应商的恢复能力更强. 也即是,λ表示供应商的可靠性,λ越大, 可靠性越差,μ/λ表示供应商的敏捷性,μ/λ越大, 敏捷性越强, 可靠性和敏捷性从两个角度综合反映了供应商的供货能力.

从可靠性的角度, 如图4所示, 在μ/λ=5的条件下,随着λ的增加, 风险中性决策者(risk neutral, 以下简称N)的最优订货量先增加后下降, 风险厌恶型决策者(risk averse, 以下简称A)则订货量保持下降趋势, 由此可见, 系统的最优订货量大小与系统的可靠性无单调关系, 可靠性越差的系统1个周期内的最优订货量水平可能会越低. 两类决策者的最优订货量偏差在λ较小的区域差异较大, 而随着λ的增加, 差异逐渐缩小, 表明决策者的风险态度在供货中断发生不太频繁的系统下对最优库存决策影响较大, 与理性最优决策出现较大偏差.

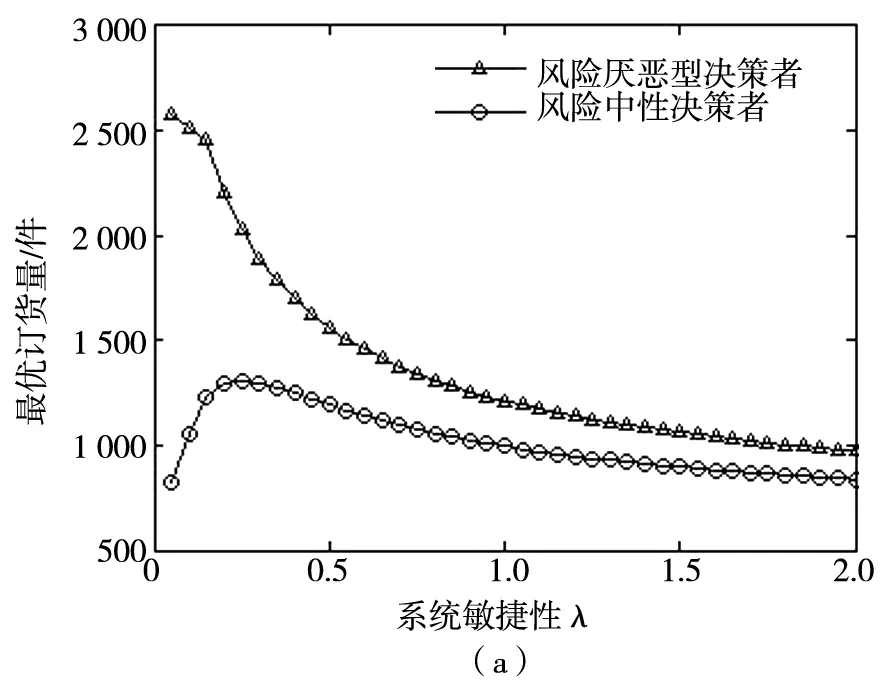
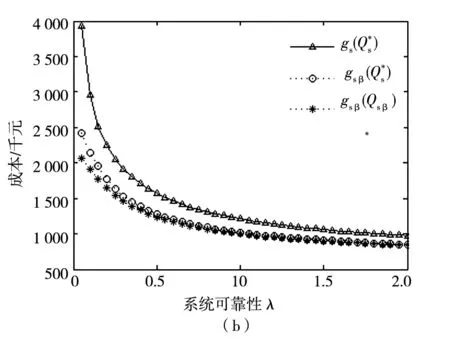
图4 最优订货量与系统成本关于可靠性λ的变化趋势(μ/λ=5)

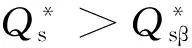
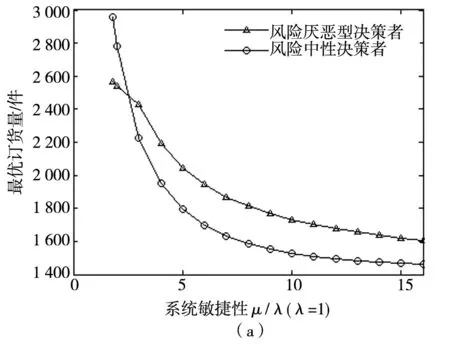
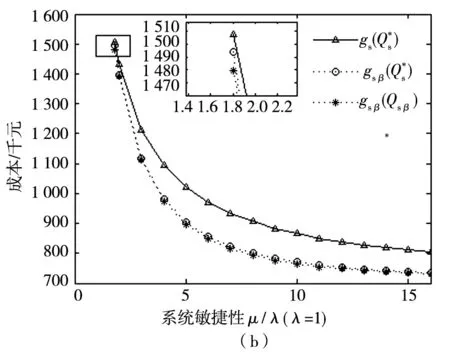
图5 最优订货量与系统成本关于敏捷性μ/λ的变化趋势

结合图4与图5, A型决策者与N型决策者最优订货量差异比随着λ增大而减小, 随着μ/λ增大而增大. 决策者的风险态度对其最优决策以及系统的运行成本有显著影响. 因此, 在构建库存优化模型时, 尤其针对供应商供货中断风险发生频率较低, 但恢复正常工作较强的这类系统, 需对决策者的风险态度进行着重区别分析.

进一步讨论缺货成本π对最优订货量以及系统成本的影响. 如图6所示, A型与N型决策者的系统成本均随着缺货成本的增加而增加. 从最优订货量的角度, N型决策者最优订货量决策对缺货成本的变化较为敏感. A型决策者最优订货量在缺货成本较小时增加速度较快, 而后逐渐趋于平稳, A型决策者最优订货量仅在缺货成本较小的区域较为敏感, 而在较大的区域范围内不敏感.

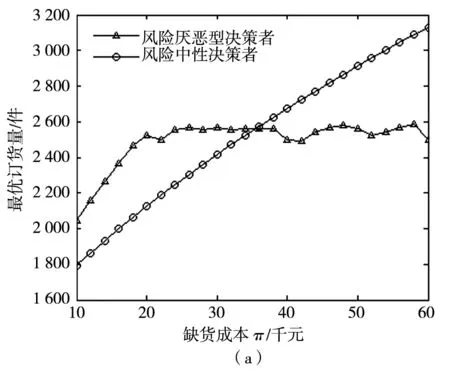
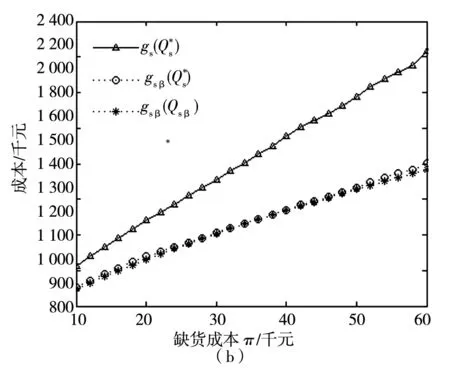
图6 最优订货量与系统成本关于缺货成本π的变化趋势

图7描述了持货成本h的变化对最优决策和系统成本的影响. A型决策者与N型决策者的最优订货量和成本关于h的变化趋势相似. 随着持货成本的增加, 最优订货量逐渐减小, 系统成本逐渐增加. 在较小的h范围内, 减小或增加的速度较快, 而在较大的h范围内, 变化速度较慢. 表明最优订货量与系统成本对于持货成本h较小时较为敏感.

图7 最优订货量与系统成本关于持货成本h的变化趋势

图8 系统近似成本g与精确成本函数gs

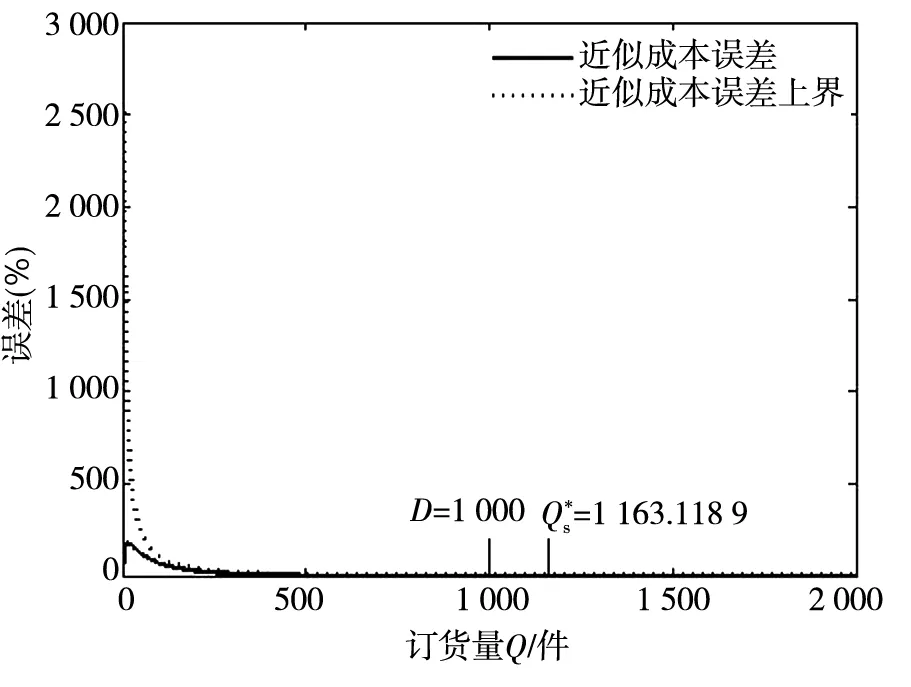
图及其上界关于Q的变化趋势图

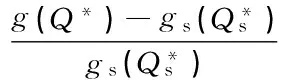
表1 成本函数近似误差

表2 最优订货量近似误差

进一步设计大规模数值实验考察近似方法的精确性, 设置基准数据集和随机数据集两类仿真数据集. 基准数据集在给定数据下进行组合计算, 随机数据集为在一定范围内进行随机取值计算. 基准集和随机数据的配合有效地增加了样本量并保证了样本取值范围的广度. 两类数据样本量分别为160组和10 000组. 基准集参数h,K,π,和D的取值如表3所示,λ=(0.5,1,2,4),μ=(2λ, 4λ, 8λ, 16λ). 在随机组中,设D=100,K～[0, 10 000],h～[0,100]. 为保证缺货成本大于持货成本(π≥h), 设置π～[h,1 000]. 计算通过MATLAB模块进行.

表3 基准集参数

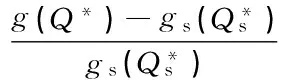
表4 成本函数近似误差及其误差上界

6 结束语

本文在连续盘点库存系统中, 讨论风险厌恶者主观高估补货点发生供货中断的小概率关键事件对最优决策以及系统成本的影响. 利用两个状态连续时间Markov链和更新报酬定理构建了长程平均成本模型, 证明了最优订货决策的惟一性. 进一步, 设计近似模型并得出最优订货量的近似解析解, 并分析了近似解的精确度,给出了近似成本误差理论上界.

与风险中性模型进行了对比讨论，结果表明, 决策者的风险厌恶偏好会增加系统运行成本, 但通过提高订货量水平并不总是经济有效的. 对于风险厌恶型决策者而言, 选择比风险中性决策者更低的订货量水平可能使得系统运行成本更低. 此外, 风险厌恶型决策者与风险中性决策者对系统参数的敏感程度也体现出显著差异. 例如, 风险中性决策者最优订货量对缺货成本的变化较为敏感. 随着缺货成本的增加, 最优订货量也相应增加. 而风险厌恶型决策者最优订货量仅在缺货成本较小的区域较为敏感, 而在较大的区域范围内不敏感.特别的, 对于供货中断风险发生不频繁, 但处理中断敏捷性较差的这类系统, 决策者的风险厌恶态度对最优订货量和系统成本的影响较大.

本文基于缺货不补的库存策略讨论决策者风险态度, 后续可进一步针对缺货回补的库存策略进行讨论. 另外, 本文聚焦于小概率高量级的风险主观性, 供应链面临的风险远不仅如此, 频繁发生或量级低的风险对库存管理的影响也有待考察.

[1]吴 军, 李 健, 汪寿阳. 供应链风险管理中的几个重要问题[J]. 管理科学学报, 2007, 9(6): 1-12. Wu Jun, Li Jian, Wang Shouyang. Some key problems in supply chain risk management[J]. Journal of Management Sciences in China, 2010, 9(4): 1-12. (in Chinese)

[2]Dada M, Petruzzi N C, Schwarz L B. A newsvendor’s procurement problem when suppliers are unreliable[J]. Manufacturing & Service Operations Management, 2007, 9(1): 9-32.

[3]Hu B, Kostamis D. Managing supply disruptions when sourcing from reliable and unreliable suppliers[J]. Production and Operations Management, 2015, 24(5): 808-820.

[4]Chen J, Zhao X, Shen Z. Risk mitigation benefit from backup suppliers in the presence of the horizontal fairness concern[J]. Decision Sciences, 2015, 46(4): 663-696.

[5]Song J S, Zipkin P H. Inventory control with information about supply conditions[J]. Management Science, 1996, 42(10): 1409-1419.

[7]Chen J, Zhao X, Zhou Y. A periodic-review inventory system with a capacitated backup supplier for mitigating supply disruptions[J]. European Journal of Operational Research, 2012, 219(2): 312-323.

[8]Parlar M, Berkin D. Future supply uncertainty in EOQ models[J]. Naval Research Logistics, 1991, 38(1): 107-121.

[9]Berk E, Arreola-Risa A. Note on “Future supply uncertainty in EOQ models”[J]. Naval Research Logistics, 1994, 41(1): 129-132.

[10]娄山佐, 吴耀华, 吕 文, 等. 随机中断环境下的库存优化管理[J]. 系统工程理论与实践, 2010, 30(3): 469-475. Lou Shanzuo, Wu Yaohua, Lü Wen, et al. Optima inventory management under stochastic disruption[J]. Systems Engineering-Theory & Practice, 2010, 30(3): 469-475. (in Chinese)

[11]Snyder L V. A tight approximation for an EOQ model with supply disruptions[J]. International Journal of Production Economics, 2014, 155(9): 91-108.

[12]SnyderL V, Atan Z, Peng P, et al. OR/MS models for supply chain disruptions: A review[J]. IIE Transactions, 2016, 48(2): 89-109.

[13]刘作仪, 查 勇. 行为运作管理: 一个正在显现的研究领域[J]. 管理科学学报, 2009, 12(4): 64-74. Liu Zuoyi, Zha Yong. Behavioral operations management: An emerging research field[J]. Journal of Management Sciences in China, 2009, 12 (4): 64-74. (in Chinese)

[14]Merzifonluoglu Y. Impact of risk aversion and backup supplier on sourcing decisions of a firm[J]. International Journal of Production Research, 2015, 53(22): 6937-6961.

[15]Giri B C. Managing inventory with two suppliers under yield uncertainty and risk aversion[J]. International Journal of Production Economics, 2011, 133(1): 80-85.

[16]Chen X, Sim M, Simchi-Levi D, et al. Risk aversion in inventory management[J]. Operations Research, 2007, 55(5): 828-842.

[17]简惠云, 许民利. 基于CVaR的供应链契约及其实验研究[J]. 管理科学学报, 2015, 18(10): 56-68. Jian Huiyun, Xu Minli. Models and their experiments of supply chain contracts based on CVaR[J]. Journal of Management Sciences in China, 2015, 18(10): 56-68. (in Chinese)

[18]代建生, 孟卫东, 范 波. 风险规避供应链的回购契约安排[J]. 管理科学学报, 2015, 18(5): 57-67. Dai Jiansheng, Meng Weidong, Fan Bo. Supply chain coordination with risk aversion via buy-back contracts[J]. Journal of Management Sciences in China, 2015, 18(5): 57-67. (in Chinese)

[19]王丽梅, 姚 忠, 刘 鲁. 现货供应不确定下的优化采购策略研究[J]. 管理科学学报, 2011, 14(4): 24-35. Wang Limei, Yao Zhong, Liu Lu. Dual sourcing optimal procurement policy under spot market supply uncertainty[J]. Journal of Management Sciences in China, 2011, 14(4): 24-35．(in Chinese)

[20]于 辉, 邓 亮, 孙彩虹. 供应链应急援助的CVaR模型[J]. 管理科学学报, 2011, 14(6): 68-75. Yu Hui, Deng Liang, Sun Caihong. A CVaR model of supply chain emergency assistance[J]. Journal of Management Sciences in China, 2011, 14(6): 68-75. (in Chinese)

[21]Ellis S C, Henry R M, Shockley J. Buyer perceptions of supply disruption risk: A behavioral view and empirical assessment[J]. Journal of Operations Management, 2010, 28(1): 34-46.

[22]Kahneman D, Tversky A. Prospect theory: An analysis of decision under risk[J]. Econometrica, 1990, 47(2): 140-170.

[23]Ranjan R, Shogren J F. How probability weighting affects participation in water markets[J]. Water Resources Research, 2006, 42(8): 1013-1016.

[24]陈俊霖, 赵晓波. 反 S 型权重风险偏好对一类两级供应链的影响[J]. 运筹与管理, 2013, 22(2): 1-7. Chen Junlin, Zhao Xiaobo. Inverse-S shaped weighting function in a two stage supply chain[J]. Operations Research and Management Science, 2013, 22(2): 1-7.(in Chinese)

[25]Chen J, Zhao H, Zhao X. How probability weighting affects inventory management with supply disruptions[J]. Lecture Notes in Engineering & Computer Science, 2012, 2196(1).

[26]Prelec D. The probability weighting function[J]. Econometrica, 1998, 66(3): 497-528.

[27]Ross S M. Introduction to Probability Models[M]. New York, London: Academic Press Inc. ninth edition, 2006: 625-627.

[28]Quiggin J. Generalized Expected Utility Theory: The Rank Dependent Model[M]. Berlin: Springer, 1992.

[29]Porteus E L. Foundations of Stochastic Inventory Theory[M]. Stanford: Stanford University Press, 2002.

Inventory model with inverse S-shaped probability weighting in presence of supply disruptions

CHENJun-lin1,ZHAOXiao-bo2,WANGXiao-jie2

1. School of Management Science and Engineering, Central University of Finance and Economics, Beijing 100081, China;2. Department of Industrial Engineering, Tsinghua University, Beijing 100084, China

This paper considers a continuous-review inventory system which applies zero-inventory-order (ZIO) replenishment policy and which is subject to supply disruption risk. The supplier’s available and disrupted durations are assumed to follow two independent exponential distributions. A risk-averse manager is likely to overweigh the probability that the supplier is unavailable when the inventory level reaches the reorder point. An inverse-S shaped weighting function is used to describe the manager’s risk-aversion behavior. The supplier’s state transition process is modeled by a two-state continuous-time Markov chain, and the long-run average cost function is constructed according to renewal reward theorems. It is proved that the negative cost function is a unimodal function and that there exists a uniquely optimal inventory order quantity. An approximation method along with an upper bound of the approximated cost function error is proposed which can give the analytic expression for the optimal order quantity. Numerical studies are presented to investigate the biases on optimal order quantities and system costs between risk-averse and risk-neutral managers. Also, with a sample size of 160 benchmark sets and 1 000 random sets, the validity of approximation method is illustrated.

supply disruption; inverse-S shaped weighting function; risk aversion; inventory

2014-12-09；

2016-03-07.

国家自然科学基金资助项目(71401195； 71031005； 91324203)； 中央高校基本科研业务费专项基金中央财经大学科研创新团队支持计划资助项目.

陈俊霖(1983—)， 女， 四川巴中人， 博士， 副教授. Email: chenjunlin@cufe.edu.cn

F253.4

A

1007-9807(2016)12-0059-12