长河坝水电站初期施工导流方案的风险决策研究

周德彦，李学权，刘亚洲

(中国电建集团成都勘测设计研究院有限公司，四川成都610072)



长河坝水电站初期施工导流方案的风险决策研究

周德彦，李学权，刘亚洲

(中国电建集团成都勘测设计研究院有限公司，四川成都610072)

水电站施工导流方案的决策是一个复杂的不确定性问题。通过引入区间数学理论和群组决策思想，建立风险决策区间分析方法对水电站施工导流方案进行决策。该方法采用区间数表示评价指标属性值，体现其风险决策过程所具有的不确定性；基于群组决策的不确定型AHP法确定评价指标的权重，便于充分利用专家群体的智慧和经验。将该分析方法应用于长河坝水电站工程中的初期施工导流方案中，对30年一遇和50年一遇的施工导流标准进行风险决策，应用结果验证了所建立的分析方法合理可行。

施工导流；风险决策；区间数学理论；群组决策；风险分析方法；长河坝水电站

1 工程概况

1.1 研究背景

水电工程的施工导流影响着其建设全过程，施工导流标准的确定非常重要，不仅影响整个工程的施工安全，也影响着工期和工程造价。在水电工程建设中，选择经济可行的导流标准，确定合理可行的导流方案，有助于减少建设造价和缩短施工工期。

长河坝水电站作为我国西南水电开发的许多大型工程之一，为一等大(1)型工程，坝址处河谷狭窄、地势险峻。如何在考虑费用、工期及风险等父母因素，最终确定一个最优方案是一个很大的难题。由于上述指标单位不一样，衡量的标准也不一样(即存在不可公度性)。因此，研究这类具有不确定性区间数、多属性决策问题具有重要的理论意义和实际应用价值，引入风险分析理论进行研究时一种良好的研究途径。

1.2 工程背景

长河坝水电站枢纽工程由砾石土心墙堆石坝、左岸引水发电系统、右岸一条深孔泄洪洞、两条开敞式泄洪洞和一条放空洞等建筑物组成。电站总装机2 600 MW，正常蓄水位1 690.00 m，坝顶高程1 697.00 m，最大坝高约240.0 m，总库容11.4亿m3。

2 风险决策分析方法

2.1 综合评价模型

建立施工导流方案风险决策的综合评价模型，根据现有的相关研究成果，其基本原理如图1 所示。本模型由方案层、准则层(或指标层)及目标层3个层次组成，采用该模型确定最优方案就是对方案层的n个方案以准则层的影响因素和评价指标为基础进行区间关联优化分析，进行风险决策，进而得到最优方案。

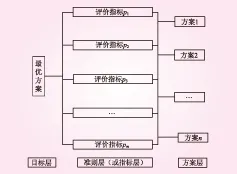
图1 综合评价模型

2.2 计算模型

要建立基于区间数学理论的施工导流方案风险决策计算模型。首先，必须建立评价指标区间属性值确定方法，并对其进行归一化处理，建立评价指标区间数决策矩阵的确定方法，进而确定理想最优方案区间数的向量，构造基于区间数的比较判断矩阵，计算出区间数权向量，并通过此结果得出各施工导流的区间关联度，对区间关联度进行相对优势度的分析，确定出最优方案。

2.2.1 评价指标区间数确定方法

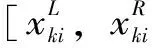
(2)定性评价指标区间属性值确定。设pi为施工导流工程中的定性评价指标，本文参考 MacCrimmon 的两极比例法，将评价指标定性评语转化为定量值的数轴法，如表1所示，即把 0～1区间分成9段，每段分别采用不同的可能性评语与数值相对应。在实际工程当中，不同的评价指标由 3～5位专家根据实际情况给出相应的定性评语，并依据表1得出相应的定量值，最后统计可得出定性评价指标区间属性值。

表1 数轴法指标转换

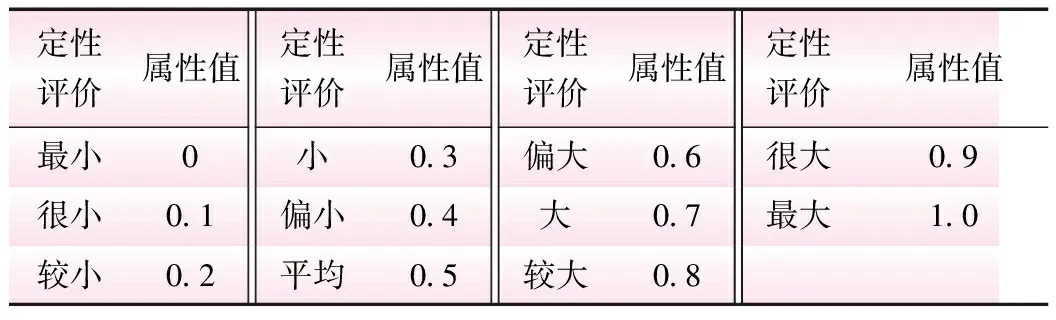
定性评价属性值定性评价属性值定性评价属性值定性评价属性值最小0小03偏大06很大09很小01偏小04大07最大10较小02平均05较大08

由上述方法确定的定量或定性评价指标区间属性值可表示成矩阵形式，即区间数决策矩阵，记为

(1)

式中，X为m个评价指标对第n个支护方案的决策矩阵；k第k第个施工导流方案，第k行表示区间数向量，由其方案影响因素第i个评价指标pi对其Dk的区间属性值构成；i为m个评价指标中的第i个评价指标，第i列表示区间数向量，由其影响因素第i个评价指标pi对n个其方案区间属性值构成。

2.2.2 归一化处理

对区间数决策矩阵进行归一化处理，便于对其进行分析处理。施工导流方案的评价指标集pi，按经济性分有成本型和效益型两种类型。在分析之前需要对其进行归一化处理，使之转化成统一的表达形式。对于区间数决策矩阵中区间属性值归一化处理的方法，有如下几种：

设pi为成本型评价指标，那么

(2)

pi为效益型评价指标，那么

(3)

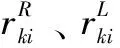
当评价指标区间属性值归一化处理之后，区间数决策矩阵R可记为X。

2.2.3 最优方案区间数

对施工导流方案风险决策进行区间优化分析之后，还需要明确关联分析所要的理想最优方案的区间数向量，区间数向量由不同的施工导流方案对应的评价指标最优区间属性值得到，是一个假想向量，只是作为区间关联分析的参照体出现。

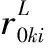
(4)

至此，可得由 S 构成的施工导流理想最优方案的区间数向量。

2.2.4 区间数权向量确定

表2 标度规则

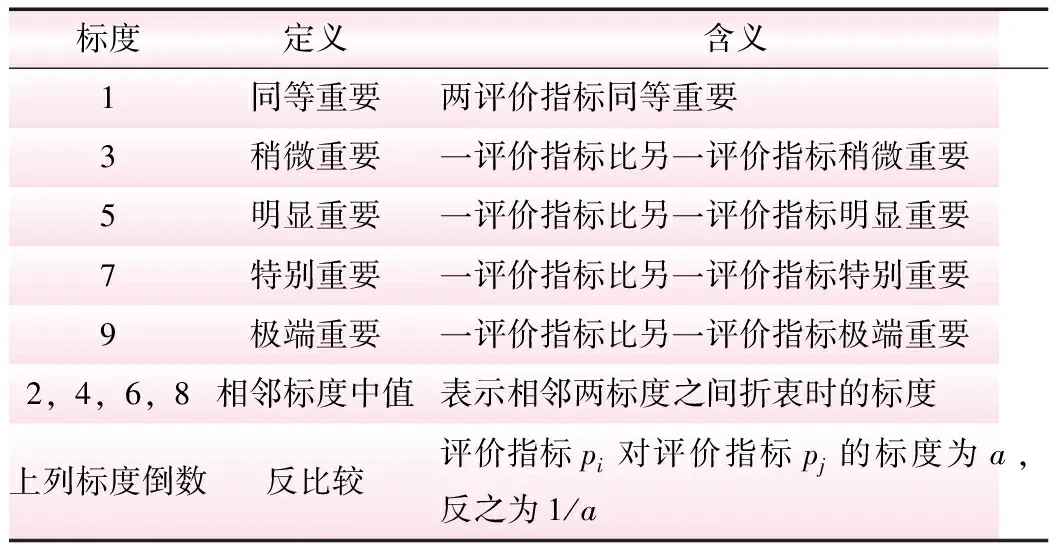
标度定义含义1同等重要两评价指标同等重要3稍微重要一评价指标比另一评价指标稍微重要5明显重要一评价指标比另一评价指标明显重要7特别重要一评价指标比另一评价指标特别重要9极端重要一评价指标比另一评价指标极端重要2，4，6，8相邻标度中值表示相邻两标度之间折衷时的标度上列标度倒数反比较评价指标pi对评价指标pj的标度为a，反之为1/a

(2)计算单个专家评价指标的权重。记第l位专家得到m个评价指标的权向量为，显然，不同专家得到的权向量并不相同。

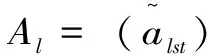
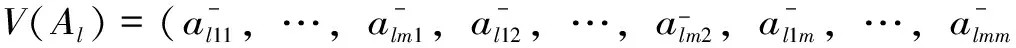
(5)

(6)

(7)

式(7)中相似度λl反映出了专家Gl与其他专家所给的判断矩阵的相似度，如果相似度越高，则Al的可信度就越高，则他在群组决策中的作用相应的就越大。②计算不确定型判断矩阵的差异度。设专家Gl所给判断矩阵Al的导出向量为V(Al)，令：

(8)

(9)

式中，alf(f=1,2,…,2m2)为判断矩阵Al的导出向量V(Al)的第f个元素，δl为第l个专家与其他专家所给判断矩阵的差异度，其和相似度一样能够从另一个角度反映专家评判的可信度。③综合考虑相似度和差异度计算专家结论的可信度(专家自身权重)。若相似度λl越大、差异度δl越小，则Al可信度越高，其在群组决策中的作用也应越大，故专家可信度rl计算可采用如下方法：

(10)

(4)计算考虑专家可信度的评价指标权重。考虑专家可信度，整合各位专家所给的评价指标权重结果。①基于专家可信度采用下式计算二级评价指标及其所含一级评价指标的区间数权向量，即

(11)

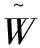
(12)

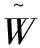
(13)

2.2.5 区间关联度的确定

引用区间数权向量、理想最优方案区间数向量及归一化决策矩阵进行施工导流方案风险决策的区间关联模糊优化分析，首先应建立出区间关联度的确定方法。可得到所有施工导流方案与理想最优方案对应评价指标的关联系数，然后采用权重加权求和得到施工导流方案Dk对理想最优方案区间数向量S的区间关联度为

ζk=ζk=∑ξk(pi)wi

(14)

式中，ξk为准则层指标层评价指标综合影响的各施工导流方案关联度。根据关联度最大原则即可得到施工导流最优方案，即哪个方案的关联度ξk最大，则该方案最优。

3 长河坝工程初期导流方案实例分析

3.1 风险决策背景

类比国内在建或已建同坝型工程导流标准，对于长河坝水电站导流标准提出了30年一遇与50年一遇两个不同的导流标准，需要综合考虑多个评价指标来对这2个不同的导流标准进行风险决策。

长河坝水电站上、下游围堰必须在河道截流后至次年的汛前完建。根据本工程地处高山峡谷的特点，对围堰的规模、施工条件、施工方法和施工进度进行综合分析研究，并参照国内大型工程如小浪底、二滩等工程围堰施工，上游围堰高度宜控制在50.0～60.0 m。

不同导流标准工程围堰的相关经济技术指标比较如表3所示。

表3 30年、50年一遇导流标准围堰工程经济技术指标比较

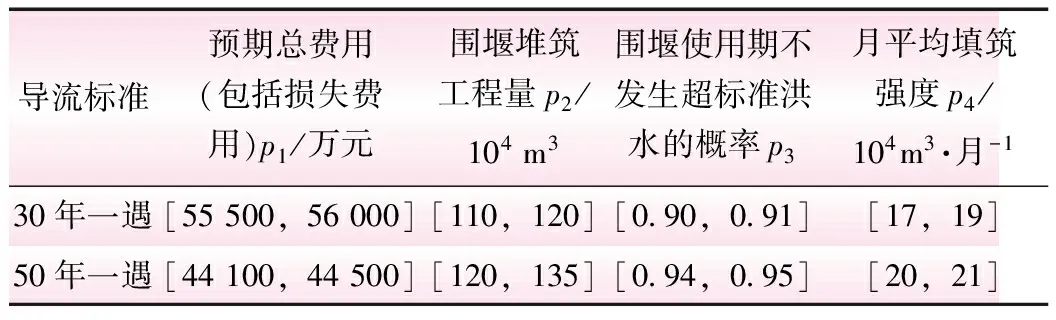
导流标准预期总费用(包括损失费用)p1/万元围堰堆筑工程量p2/104m3围堰使用期不发生超标准洪水的概率p3月平均填筑强度p4/104m3·月-130年一遇[55500，56000][110，120][090，091][17，19]50年一遇[44100，44500][120，135][094，095][20，21]

3.2 决策过程

采用本文建立的风险决策区间分析方法对上述2个施工导流标准进行风险决策。

(1)确定评价指标。根据表3，本文选取预期总费用(包括损失费用)p1、围堰堆筑工程量p2、围堰使用期不发生超标准洪水的概率p3以及月平均填筑强度p4等4个评价指标进行风险决策。

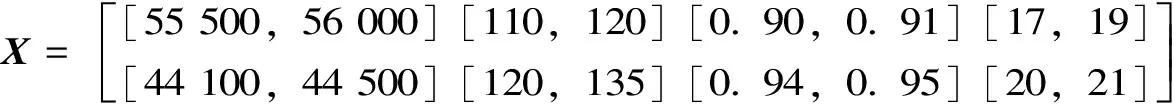
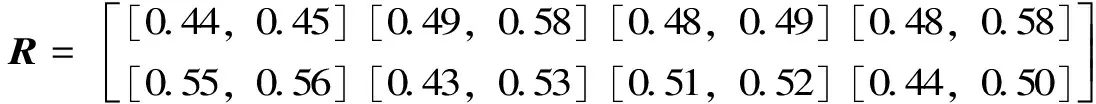
(4)确定理想最优方案区间数向量。利用归一化区间数决策矩阵R对施工导流方案风险决策进行区间优化分析，还必须确定出关联分析所需要理想最优方案的区间数向量，可得影响因素所含4个评价指标pi的理想最优方案区间数向量为S={[0.55,0.56],[0.49,0.58],[0.51,0.52],[0.48,0.58]}。

(5)确定区间数权向量。由于不同专家判断结果的可信程度不同，同时也由于专家在判断两两因素相对重要程度时不可能绝对准确，只能给出一个区间范围，本文邀请了4位专家构造不确定型判断矩阵，分别如表4～7所示。根据计算出的区间数权重计算方法得到评价指标p1、p2、p3、p4的权重分别为0.36、0.22、0.27、0.15。

表4 判断矩阵A1

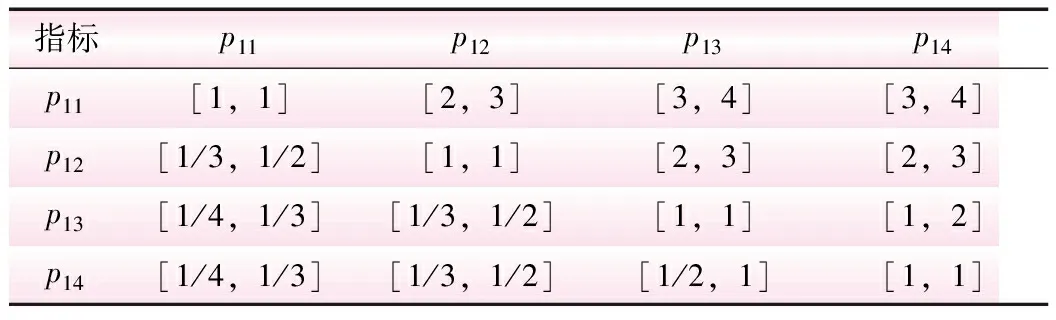
指标p11p12p13p14p11[1，1][2，3][3，4][3，4]p12[1/3，1/2][1，1][2，3][2，3]p13[1/4，1/3][1/3，1/2][1，1][1，2]p14[1/4，1/3][1/3，1/2][1/2，1][1，1]

表5 判断矩阵A2

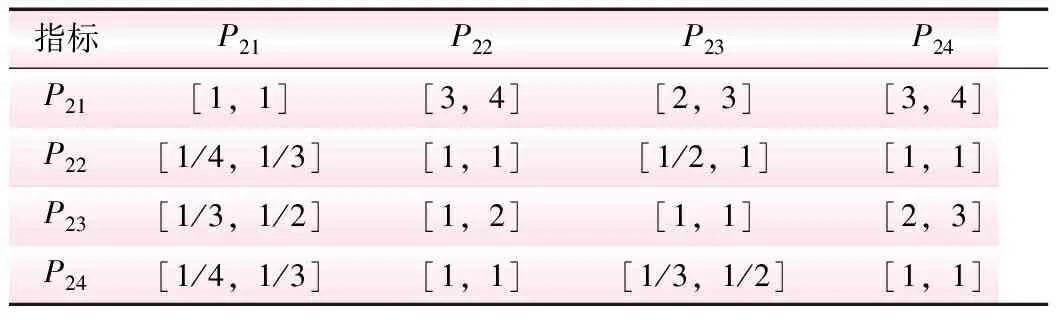
指标P21P22P23P24P21[1，1][3，4][2，3][3，4]P22[1/4，1/3][1，1][1/2，1][1，1]P23[1/3，1/2][1，2][1，1][2，3]P24[1/4，1/3][1，1][1/3，1/2][1，1]

表6 判断矩阵A3

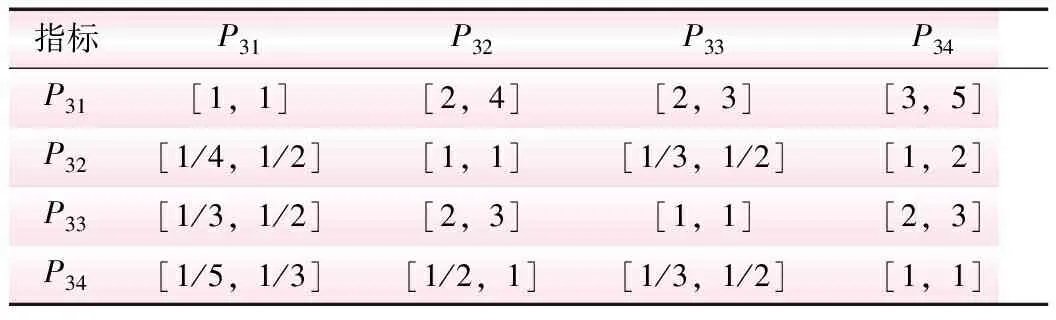
指标P31P32P33P34P31[1，1][2，4][2，3][3，5]P32[1/4，1/2][1，1][1/3，1/2][1，2]P33[1/3，1/2][2，3][1，1][2，3]P34[1/5，1/3][1/2，1][1/3，1/2][1，1]

表7 判断矩阵A4

指标P41P42P43P44P41[1，1][3，4][2，4][4，5]P42[1/4，1/3][1，1][1/2，1][2，3]P43[1/4，1/2][1，2][1，1][3，4]P44[1/5，1/4][1/3，1/2][1/4，1/3][1，1]

3.3 决策结论

如果仅根据单个评价指标进行风险决策，则对于不同的评价指标可能会得到不同的风险决策结果。根据表3可知，如果仅考虑围堰堆筑工程量，则30年一遇比50年一遇的导流标准更加合理，而如果仅考虑预期总费用这一评价指标，则50年一遇比30年一遇的导流标准更加合理。对于长河坝工程有必要综合考虑多个评价指标进行风险决策。

类比国内工程长河坝水电站初期导流标准采用50年一遇是合适的。根据堆筑工程量的分析，50年一遇较30年一遇上游堰高增加4.8 m，堆筑方量增加21.20万m3；下游围堰在堰高、堆筑方量上相差甚微，因此两种导流标准的堆筑工程量比较接近，此外，两个导流标准的预期总费用分别如表8所示，50年一遇方案的总费用较小，风险度较低，要优于30年一遇方案。故经过论证分析，最终确定施工导流标准为50年一遇，这与本文方法所得到的风险决策结果一致，从而证明了本文所提方法合理可行。

表8 单目标各导流方案预期总费用 万元

4 结 语

本文引入了区间数学理论和群组决策思想，对施工导流方案风险决策方法进行了深入的研究，提出了施工导流方案风险决策的区间分析方法，并针对长河坝水电站施工导流标准进行具体分析。根据长河坝水电站施工导流影响因素存在不确定性的特点，分别选取4个评价指标来综合考虑多个因素的影响，采用区间数来描述评价指标的指标值，并考虑到不同专家限于自身的研究领域限制以及经验的不同，提出采用群组决策的思量融合多个专家的评价结论，从而提高了权重计算的可信度，通过施工导流标准的工程实例表明，本文建立的施工导流方案风险决策区间分析方法的计算结果与实际结果相吻合，从而验证了本文方法的可行性和合理性。

[1]中国水电顾问集团成都勘测设计研究院. 长河坝水电站可研报告施工组织设计[R]. 成都： 中国水电顾问集团成都勘测设计研究院， 2009．

[2]周德彦. 长河坝水电站施工导流方案风险决策研究[D]. 南京： 河海大学， 2012.

[3]覃晖. 流域梯级电站群多目标联合优化调度与多属性风险决策[D]. 武汉： 华中科技大学， 2011．

[4]徐森泉， 胡志根， 刘全， 等. 基于多重不确定性因素的施工导流风险分析[J]. 水电能源科学， 2004， 22(4)： 78- 81

[5]范锡峨， 胡志根， 靳鹏. 基于Monte-Carlo方法的施工导流系统综合风险分析[J]. 水科学进展， 2007， 18(4)： 604- 608．

[6]陈志鼎， 胡志根. 施工导流工程风险的保险费用厘定方法研究[J]. 中国工程科学， 2011， 13(4)： 106- 112．

[7]胡志根， 等. 施工导流风险分析[M]. 北京： 科学出版社， 2010．

[8]褚茁， 胡志根， 刘全. 考虑施工进度影响的锦屏一级水电站导流全过程风险分析[J]. 武汉大学学报： 工学版， 2012， 45(2)： 161- 165．

[9]兰继斌， 徐扬， 霍良安， 等. 模糊层次分析法权重研究[J]. 系统工程理论与实践， 2006(9)： 107- 112．

[10]陈可， 陈晓红. 一种基于区间数判断矩阵的加权AIP群决策方法[J]. 控制与决策， 2009， 24(9)： 1042- 1046．

[11]章恒全， 林武星. 单次洪灾经济损失评价方法研究[J]. 水利经济， 2007， 25(6)： 13- 15.

[12]潘仁飞， 邹乐乐， 侯运炳. 基于专家可信度的不确定型AHP方法及其应用[J]. 系统工程， 2008， 26(10)： 101- 106．

[13]陈春丽， 刘永强， 于良， 等. 基于ELECTRE- 1法的施工导流方案优选[J]. 水电能源科学， 2012， 30(4)： 55- 57．

(责任编辑 王 琪)

Research on Risk Decision-making of Early Construction Diversion Schemes of Changheba Hydropower Station

ZHOU Deyan, LI Xuequan, LIU Yazhou

(PowerChina Chengdu Engineering Corporation Limited, Chengdu 610072, Sichuan, China)

The decision-making of hydropower station construction diversion scheme is a complex uncertainty problem. By introducing interval mathematical theory and group decision-making idea, a risk decision-making interval analysis method is established to select construction division scheme of hydropower. station The interval number is used to represent the property value of evaluation index in this method, which reflects the uncertainty of risk decision-making process. The weight of evaluation index is determined by uncertain AHP based on group decision-making idea, which can facilitate the use of experts’ experiences. The method has been used in early construction division scheme analyses of Changheba Hydropower Station to evaluate the risks of construction division schemes under the floods with 30-year frequency and 50-year frequency respectively. The application has verified the feasibility of proposed method．

construction diversion; risk decision-making; interval mathematical theory; group decision; risk analysis; Changheba Hydropower Station

2016- 08- 03

周德彦(1982—)，女，河南南阳人，高级工程师，硕士，主要从事国内外水利水电、光伏风电场等工程的施工组织设计工作．

TV551.16(271)

A

0559- 9342(2016)10- 0049- 05