基于Beggs & Brill模型的油田水力集输半径分析

罗 珊 蒋宏业 姚安林 江 文 曾跃辉

西南石油大学石油与天然气工程学院， 四川 成都 610500



基于Beggs & Brill模型的油田水力集输半径分析

罗 珊 蒋宏业 姚安林 江 文 曾跃辉

西南石油大学石油与天然气工程学院， 四川 成都 610500

带倾角的多相流管路工况复杂，集输半径不能根据经验直接获取，为此需建立完整的集输半径计算模型。基于流态划分的油田集输半径确定主要包括压降公式的选用、流态确定、摩阻系数的计算、截面持液率方案选取。常用的Beggs & Brill压降公式没有直接的流型计算方法，采用改进的Barnea流态公式结合修正后的Beggs & Brill持液率计算公式来弥补。以某油田集输管网为例，运用此方法得出的带倾角管路集输半径与约束条件下的实际集输半径基本相符。

集输半径；流态划分；倾斜管路；组合模型

0 前言

在油田地面工程的方案设计中，集输半径指在满足最低进站压力的条件下，井口回压可驱动管道内原油输送的距离，它直接影响井组划分、站址选择和管网流量分配，间接影响集输系统总造价。在油田单井管线的油气集输工艺中，人们通过长期实践，将2～3 km作为单井集输的集输半径，但这个集输半径有很多不合理的地方[1]：该集输半径主要针对地势较平坦的区域，没有考虑到油区内管线有较大的爬升和下降地段的重力压降对集输的重要影响；对不同性质的油品，用统一的标准会造成输送动力的不足或过剩，从而严重影响油气输送。因此选择合理的集输半径具有重要意义[2]。

GB 50350-2005《油气集输设计规范》中提出，油气混输的压降计算采用DuklerⅡ法[3-4]和Beggs & Brill法。DuklerⅡ法适用于水平管路，单纯的Beggs & Brill法不能解决基于流态划分的直接计算。李时宣等人[5]根据西峰油田集输管路的特点，结合DuklerⅡ法和Beggs & Brill法，提出计算两相水平管路水力集输半径的CY法；

张友波[6]研究了气液两相管流技术并开发了工艺计算软件，但这些方法在计算带倾角两相流动管路的集输半径时并不准确。本文带倾角管路的集输半径计算方案通过查阅大量的经验公式并结合实际进行模型比较得出。

1 带倾角管路集输半径的界定

1.1 采用改进Beggs & Brill法的水力分析

1)根据井口回压P0和最低进站压力P1计算管路平均压力以及压降。

2)结合压降公式，选用适当的方法划分流态，计算沿程摩阻系数和截面含液率。

3)根据现场情况确定相应的参数，包括不同流态下气液相折算速度，体积含液率，管路倾角和表面张力等。

1.2 带倾角管路集输半径计算模型

表1列出了6种常用的考虑倾角的气液两相流动管路集输半径计算模型。

表1 气液两相流动管路集输半径计算模型

组合模型代码流态划分截面含液率选用压降公式选用BB*-BAR*-MBBAR*BB*MBBB-BAR-XBBARBBXBBB*-BB-MBBBBB*MBBB-XB-BBBBBB-XBBBBB*-BAR*-BBBAR*BB*BBBB-XBBBBB-XBXB 注:BB*为在计算倾斜管的持液率时用修正的Beggs&Brill公式;BAR*为用修正的Barnea公式来确定流态的划分;BAR为Barnea流态划分公式;XB为Xiao-Brill压降公式;MB为Mukherjee&Brill压降公式;XB-BB为Xiao-Brill和Beggs&Brill截面持液率的组合表达式;BB为Beggs&Brill相关式。

2 确定组合模型

2.1 压降公式的选用

常见的气液两相流动压降公式包括DuklerⅡ公式、Eaton公式、Flanigan公式、Beggs & Brill公式、Mukherjee & Brill公式、Xiao-Brill公式等[7-8]。其中只有Flanigan公式、Beggs & Brill公式、Mukherjee & Brill公式和Xiao-Brill公式考虑了管路倾角。公式的选用需要结合现场实际情况，但在实验数据缺乏时只能借助对比分析来选取。对于气液两相带倾角管路，根据经验方法和设计规范相关内容，选用Beggs & Brill公式[9]：

(1)

式中：ρi为液相密度，kg/m3;ρg为气相密度，kg/m3；θ为管路倾角，度或弧度；G为气液混合物质量流量，kg/s;Hi为截面含液率，无因次量；dP为管道压降，Pa；dx为管路压降驱动气液混合物流动的距离，m；P为管道内介质的平均绝对压力，Pa；wsg为气相折算流速,m/s；d为管道内径，m；wm为气液混合物速度，m/s；i为常数，代表井号；针对Beggs & Brill公式没有考虑流态划分问题，混合摩阻系数λm按照不同流态下的公式计算得出并带入式(1)求解。

2.2 水力摩阻系数的计算

多数多相流研究者认为[7]，在多相管流中，气体或液体与管壁之间摩阻系数的计算可以采用单相流中沿程摩阻系数的计算方法。而气液界面之间的沿程摩阻系数只能采用多相管流中的经验或半经验公式，喻西崇等人[10-13]进行了大量的研究。本文选用Xiao J J等人[14]提出的计算气液界面间摩阻系数的方法。该方法在划分流态的基础上得出，满足基于流态划分的持液率计算公式。

2.2.1 对于分离流

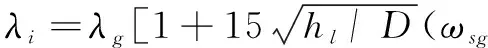
(2)

式中：λg为气体与管壁间的摩阻系数，采用单相流的方法计算；hl/D为液位高度与管径的比值，可采用二分法迭代求解，求解时在某些情况下会出现多重根，通常取最小值为计算值。

2.2.2 对于间歇流

λi=λc{1+2 250(δ/D)/[ρg(ωsg-ωsl)2δ/σ]}

(3)

式中：λc为气芯摩阻系数，无量纲；δ为液膜厚度，m；ωsg为气相折算速度，kg/m;ωsl为液相折算速度，kg/m；σ为表面张力，N/m；D为管道外径，m；ρg为气相密度，kg/m3；δ/D用二分法迭代求出。

2.2.3 分散流

对于分散流λi统一取0。

2.3 持液率计算方法的选取

常用的截面含液率计算方法都是在实验基础上得出的，对于倾角管路用Beggs & Brill模型两相流持液率公式，其上、下坡管道的持液率计算分别采用以下两点改进[15-17]：

1)Payne G A等人[18]基于实验数据，对上坡段倾斜管道持液率公式进行修正，见式(4)。

(4)

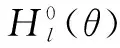
2)在下坡段，采用Xiao & Brill模型，见式(5)～(6)。

(5)

θ=2 cos-1(1-2hl/D)

(6)

式中：hl/D为液位高度与管径的比值，计算方法同式(2)；Hl(θ)为截面含液率，无因次量；θ为管路倾角，度或弧度。

2.4 流态确定

目前普遍应用的流态判定方法包括查图法和公式计算法，公式计算法较查图法适用范围更广。在Beggs & Brill公式中，截面含液率计算公式建议采用Beggs & Brill流态划分方法，但是在用此方法判断时发现[7]，气油比在0～170 m3/m3变动时，管路流型均为过渡流，在实际的低温原油管路运行中是不可能出现的，因此选用适用于所有倾角管路的Barnea相关改进公式判断流态。改进的Barnea模型计算流程图见图1。

图1 改进的Barnea模型计算流程图

图1中式(7)表示分散流向其他流型转变的相关公式，采用经Barnea修正的Taitel分散流模型计算法，该计算法适用于所有倾角范围[20]。

(7)

式中：dc为dCD和dCB的最小值；dCD为气泡变形的临界体积，cm3；dCB为阻止气泡移动到管道顶端的临界气泡体积，cm3；其他参数含义见式(1)、(3)。

图1中式(8)表示分层流转变为非分层流的相关公式，式(9)表示分离流与间歇流之间的转变公式，其中按照相态的分布特点，分层流属于分离流的一种，故可用公式(8)、(9)区分属于分离流还是间歇流。

(8)

(9)

2.5 集输半径计算公式

根据以上分析，集输半径可确定为式(10)。

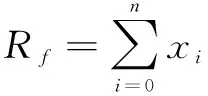
(10)

式中：n为常数，代表井号；xi由式(1)通过积分和变形得出，代表单井井口回压可驱动的管道内原油输送的距离，m。

(11)

3 实例计算

某油田集输管网的部分参数见表2。

1)根据本文模型，表3给出了部分倾角下集输半径的计算值。

此结果与现场实际集输半径相符，误差范围为±7%。

2)假设倾角不变，取不同的井口回压和气油比，分别计算得出集输半径。图2为井口回压分别为1.7 MPa和2.5 MPa的集输半径曲线图。

表2 某油田的部分参数

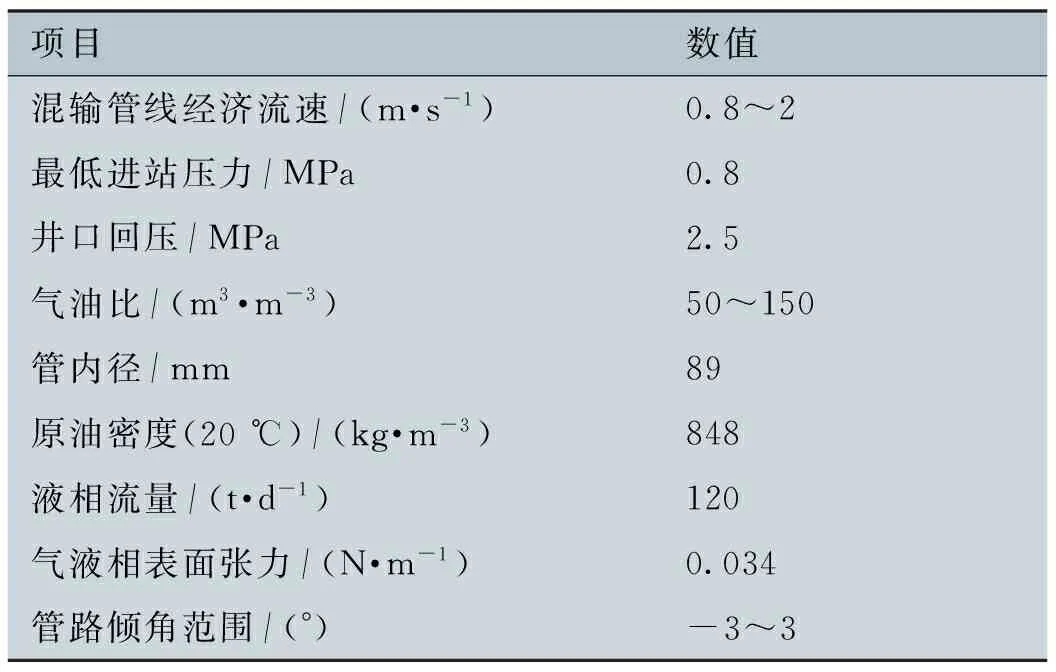
项目数值混输管线经济流速/(m·s-1)0.8～2最低进站压力/MPa0.8井口回压/MPa2.5气油比/(m3·m-3)50～150管内径/mm89原油密度(20℃)/(kg·m-3)848液相流量/(t·d-1)120气液相表面张力/(N·m-1)0.034管路倾角范围/(°)-3～3

表3 部分倾角计算出的集输半径

气油比/(m3·m-3)管路倾角/(°)集输半径/m50水平712050161531002374210033190

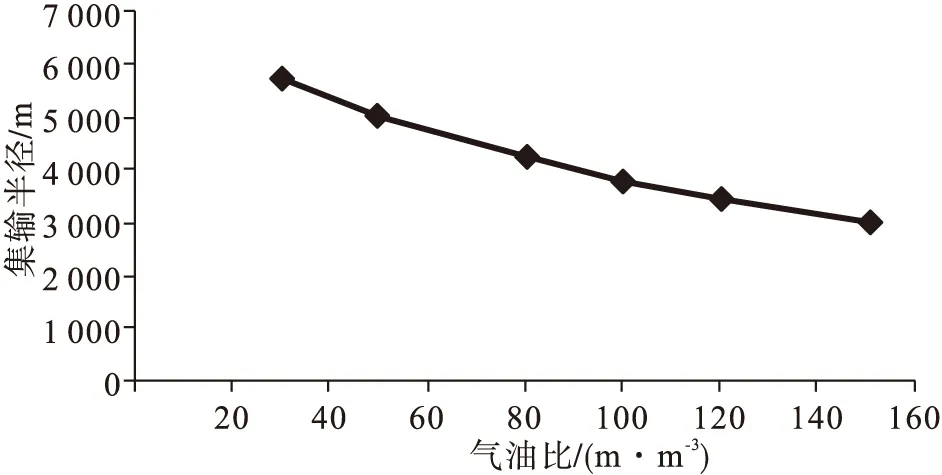
a)井口回压1.7 MPa

b)井口回压2.5 MPa图2 不同井口回压的集输半径曲线图

根据以上分析可知，带倾角管路的集输半径与相同条件下的无倾角管路集输半径相差较大，与集输半径经验数据2～3 km不符，可参照本文重新计算。

4 结论

1)在确定带倾角管路的集输半径时，只用Beggs & Brill法不能解决问题。基于Beggs & Brill模型的集输半径改进算法，可以有效地解决带倾角管路的流型划分、截面含液率和集输半径计算等问题，计算的集输半径符合油田的实际情况。

2)按照本文的方法得出的数据在油田井场划分过程中可作为基础数据应用。集输半径的精确值需要在管网划分之后，结合实际进行回压校验，考虑是否需要设热泵站之后再计算得到。

[1] 彭方宇.低渗透油田地面油气混输特性及集输界限研究[D].西安:西安石油大学,2012. Peng Fangyu. Study on Characteristics of Oil and Gas Transportation in Low Permeability Oil Field and Boundary of Gathering and Transportation [D]. Xi’an: Xi’an Petroleum University, 2012.

[2] 蒋 洪,张 黎,任广欣.煤层气地面集输管网优化[J].天然气与石油,2013,31(1):8-12. Jiang Hong, Zhang Li, Ren Guangxin. CBM Surface Gathering Pipeline Network Optimization [J]. Natural Gas and Oil, 2013, 31 (1): 8-12.

[3] Taitel Y, Lee N, Dukler A E. Transient Gas-Liquid Flow in Horizontal Pipes: Modeling the Flow Pattern Transitions [J]. Aiche Journal, 1978, 24 (5): 920-934.

[4] Taitel Y, Dukler A E. A Model for Prediction Flow Regime Transitions in Horizontal and Near Horizontal Gas-Liquid Flow [J]. Aiche Journal, 1976， 22 (1): 43-55.

[5] 李时宣,李传宪.西峰油田原油集输半径的计算分析[J].油气田地面工程,2006,25(3):6-9. Li Shixian, Li Chuanxuan. Calculation and Analysis of The Radius of Oil Gathering and Transportation in Xifeng Oilfield [J]. Oil and Gas Field Surface Engineering, 2006, 25 (3): 6-9.

[6] 张友波.气液两相管流技术研究及其工艺计算软件开发[D].成都:西南石油学院,2005. Zhang Youbo. Liquid Two-phase Pipe Flow Calculation Software Technology Research and Technology Development [D]. Chengdu: Southwest Petroleum Institute, 2005.

[7] 李长俊,贾文龙.油气管道多相流[M].北京:化学工业出版社,2014：80-160. Li Changjun, Jia Wenlong. Multiphase Flow of Oil and Gas Pipelines [M]. Beijing: Chemical Industry Press, 2014： 80-160.

[8] 张友波,李长俊,杨 静.油气混输管流中压降和持液率的影响因素分析[J].天然气与石油,2005,23(5):9-12. Zhang Youbo, Li Changjun, Yang Jing. Influencing Factor Analysis of Pressure Drop and Liquid Holdup in Oil Gas Mixed Phase Flow [J]. Natural Gas and Oil, 2005, 23(5): 9-12.

[9] Beggs H D, Brill J P. A study of Two Phase Flow in Inclined Pipes [J]. Journal of Petroleum Technology， 1973, 25 (5): 607-617.

[10] 喻西崇,冯叔初.多相管流中沿程摩阻系数分析[J].油气田地面工程,2001,20(2):3-6. Yu Xichong, Feng Shuchu. Analysis on Frictional Coefficient of Multi-Phase Pipe Flow [J]. Oil and Gas Field Surface Engineering, 2001, 20 (2): 3-6.

[11] 李玉星,冯叔初.多相流气液相间水力摩阻系数关系式评价[J].油气储运,1998,17(11):13-16. Li Yuxing, Feng Shuchu. Evaluation on Multiphase Flow between Liquid Phase and Hydraulic Friction Coefficient Formula [J]. Oil & Gas Storage and Transportation, 1998, 17 (11): 13-16.

[12] 张修刚,牛冬梅,苏新军,等.水平管内油水两相流动摩擦压降的实验研究[J].油气储运，2003,22(2):47-50. Zhang Xiugang, Niu Dongmei, Su Xinjun, et al. Study on Frictional Pressure Drop of Oil/Water Two Phase Flow in Horizontal Tube by Experiment [J]. Oil & Gas Storage and Transportation, 2003, 22 (2): 47-50.

[13] 王弥康,林日亿,张 毅.管内单相流体沿程摩阻系数分析[J].油气储运，1998,17(7):22-26. Wang Mikang, Lin Riyi, Zhang Yi.Analysis on Frictional Coefficient of Single Phase Fluid in Pipe [J]. Oil & Gas Storage and Transportation, 1998, 17 (7): 22-26.

[14] Xiao J J, Shoham O, Brill J P. A Comprehensive Mechanistic Model for Two-Phase Flow in Pipelines [C]//Paper 20631 Presented at the 65th SPE Annual Technical Conference and Exhibition, 23-26 September 1990, New Orleans, LA, USA. New York: SPE, 1990.

[15] 李玉星,喻西崇,冯叔初,等.Beggs-Brill截面含液率计算模型的剖析与修正[J].油气储运,2000,19(8)：31-34. Li Yuxing, Yu Xichong, Feng Shuchu, et al. Analysis and Modification to Liquid Holdup Calculation Model of Beggs-Brill [J]. Oil & Gas Storage and Transportation, 2000, 19 (8): 31-34.

[16] 喻西崇,赵金洲,冯叔初.起伏多相流管路持液率计算方法研究[J].西南石油学院学报,2000,22(3):94-97.

[17] 赵越超,何利民,陈振瑜.气液相流量瞬变过程强烈段塞流压力及持液率波动分析[J].天然气与石油,2007,25(1):16-18. Zhao Yuechao, He Limin, Chen Zhenyu. Analysis on Severe Slug Flow Pressure/Liquid Holdup in Gas/Liquid Flow Rate Transient Fluctuation [J]. Natural Gas and Oil, 2007, 25 (1): 16-18.

[18] Payne G A, Palmer C M, Brill J P. et al. Evaluation of Inclined-pipe, Two-phase Liquid Hold up and Pressure-loss Correlation Using Experimental Date [J]. Journal of Petroleum Technology, 1979, 18 (1)： 1198-1207.

[19] 喻西崇,冯叔初,李玉星.对Beggs & Brill相关式的改进[J].油气田地面工程,1999,18(6):1-4. Yu Xichong, Feng Shuchu, Li Yuxing. Improving to Beggs and Brill Interrelated Formulas [J]. Oil and Gas Field Surface Engineering, 1999, 18 (6): 1-4.

[20] Barnea D, Shoham O, Taitel Y. Gas-Liquid Flow in Inclined Tubes: Flow Pattern Transitions for Upward Flow [J]. Chemical Engineering Science, 1985, 40 (1): 131-136.

2015-10-11

国家“十二五”科技支撑计划项目(2011 BAK 06 B 01-11-01)

罗 珊(1991-)，女，河南南阳人，硕士研究生，主要从事油气储运专业方向的研究工作。

10.3969/j.issn.1006-5539.2016.01.006