考虑阻尼影响的动力总成悬置系统解耦研究*

孙永厚，张 骥，尹 帅，王 萌

(1.桂林电子科技大学 机电工程学院，广西 桂林 541004；2.广西制造系统与先进制造技术重点实验室，广西 桂林 541004)

考虑阻尼影响的动力总成悬置系统解耦研究*

孙永厚1,2，张 骥1，尹 帅1，王 萌1

(1.桂林电子科技大学 机电工程学院，广西 桂林 541004；2.广西制造系统与先进制造技术重点实验室，广西 桂林 541004)

为满足符合实际工况的解耦需求，针对有阻尼条件下的车辆悬置系统，建立了包含阻尼参数的动力总成悬置系统模型；然后，对比例阻尼和非比例阻尼的动力总成悬置系统进行理论分析，采用拉普拉斯变换求解有阻尼的悬置系统微分方程，计算了在比例阻尼和非比例阻尼影响下系统的固有频率；最后，利用MATLAB软件开发了相应的解耦平台，并以某型号商用车为例，在ADAMS中建立模型进行仿真验证。二者固有频率一致，证明了方法的有效性与软件结果的可靠性。

悬置系统；阻尼；解耦

0 引言

由于振动对机械结构具有破坏作用，如何减振已经成为大多数工程问题中进行机械设计和改进的必不可少的一环。汽车行驶过程中，剧烈振动会引起人体不适和汽车零部件的损坏。随着科技的发展，乘客对汽车舒适性的要求越来越高，动力总成系统的减振已经成为很多汽车厂商关注的焦点。为了控制动力总成的振动向车身传递，各大汽车厂商都设计了新的悬置，包括液阻悬置、空气悬置等，因此动力总成悬置系统解耦显得尤为重要。近年来国内对动力总成悬置系统的解耦有了深入的研究，并且得到诸多有益的成果[1-5]。吴杰，上官文斌[6]等人通过实验设计的方法，仿真分析了汽车动力总成悬置系统解耦布置的鲁棒性。付江华，史文库[7]等人采用遗传算法，兼顾固有频率和各工况下的位移，求得全局最优解，进一步提高了解耦率。目前对悬置系统的解耦研究大多集中于无阻尼的能量解耦，研究过程中很少考虑阻尼系统的影响，而工程实际的阻尼(包括结构阻尼和粘性阻尼)在悬置中起了越来越重要的作用，是不可消除的[8]。其次，阅览大部分系统解耦文献资料，大多采用振型叠加法，但这只是针对比例阻尼的解耦应用。对存在非比例阻尼的解耦，多数研究其时域响应特性，鲜有关注其固有频率这一方面的文献。

针对以上问题，本文基于扭矩轴解耦理论，以动力总成悬置系统为研究对象，建立其六自由度动力学模型，并考虑阻尼影响，对悬置系统进振动分析；其次，建立该系统的运动微分方程，以拉普拉斯变换为基础，实现微分方程由时域状态到频域状态地转变,并解出其固有频率；最后，根据上述理论开发软件，以各个方向的频率差为约束条件，通过合理配置刚度、阻尼的大小来改变系统的共振峰值，达到避免汽车发动机与其他部件产生碰撞的目的，保证汽车的行驶安全性。

1 动力总成悬置系统动力学模型

图1为动力总成悬置系统空间六自由度动力学模型。动力总成被认为是一个空间自由的刚体，通过四个具有三维弹性和阻尼的元件支撑在刚性的、质量为无限大的车架上，在此模型上建立以下坐标系。

图1 动力总成动力学模型

1.1 扭矩轴坐标系

扭矩轴[8]是无约束三维刚体的旋转轴，它与刚体的惯性特性以及施加在刚体上的扭矩有关。扭矩轴坐标系是曲轴坐标系根据相应的方向余弦矩阵旋转变换而成。以过质心平行于“扭矩轴”的轴线作为扭矩轴坐标系的X轴，Y轴和Z轴，按照坐标轴相互垂直的关系选取来建立扭矩轴坐标系，如图1中TRA坐标系所示。建立系统在扭矩轴坐标系下的振动微分方程：

(1)

式中，[M]为质量矩阵，[C]为阻尼矩阵，[K]为刚度矩阵，x为系统的响应，F(t)为系统所受激励。

1.2 虚拟样机模型

在ADAMS中建立的商用车动力总成四点悬置动力学模型，如图2所示。模型中各个悬置元件根据实际位置、安装角度输入参数，并采用力学原件Bushing来进行模拟。

图2 虚拟样机模型

2 有阻尼系统下的振动解析

动力总成橡胶悬置系统中，阻尼的数值一般很小，但是分析系统在共振点附近振动时，阻尼的影响就变得非常重要。

2.1 比例阻尼下解耦准则

阻尼总是起着降低共振峰值的作用。为了简化，阻尼矩阵C可以视为质量矩阵M与刚度矩阵K的线性组合系统，即：

C=aM+bK

(2)

式中，a、b为非负常数，一般由实验来确定。比例阻尼模型的目的是为了数学计算的方便，在求解多自由度系统的运动方程时，由于质量和刚度均有正交性，故质量和刚度可以对角化。令:

ΦTMΦ=I

(3)

ΦTKΦ=Λ

(4)

则有：

[C]=[ΦT][C][Φ]=ΦT(a[M]+b[K])Φ=
ΦTa[M]Φ+ΦTb[K]Φ=
a[I]+b[Λ]

(5)

式中，[C]即为对角矩阵。采用此方法表示阻尼矩阵的优点是：可以利用振型叠加法将动力学方程解耦，导出实模态。由于式(2)所示比例阻尼模型可以兼顾多种工况，所以在实际工程中得到了广泛的应用。

2.2 非比例阻尼的解耦准则

若阻尼矩阵C≠aM+bK，则称C为非比例阻尼矩阵，具有非比例阻尼矩阵的系统称为非比例阻尼系统。不同于比例阻尼系统导出的是实数模态，非比例阻尼系统产生的是复数模态[9]，它不能采用无阻尼的模态矩阵进行坐标变换来实现，所以需要利用状态向量法来进行求解。引入辅助方程[10]：

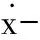
(6)

带入(1)式可得到系统状态方程：

(7)

这样就将原来的n个二阶微分方程转换为2n个一阶微分方程，设x={φ}eλt，可得特征矢方程和特征值方程：

(8)

det(λ[A]+[B])=0

(9)

可以解出n对共轭复特征值以及n对共轭的复特征矢。得到复特征值λi=σi+jωi，其中出现的σi常为负数，反映有阻尼的自由振动总是衰减的；出现的虚部ωi则是悬置系统的固有频率。

3 动力总成悬置系统解耦研究

3.1 考虑阻尼影响的悬置系统解耦

动力总成的能量解耦可以理解为：若动力总成的能量只集中于某一自由度，那么此系统沿着该自由度的振动与其他系统是没有耦合的，即为解耦状态。能量解耦率[11]为：

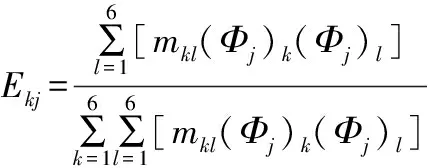
(10)

解耦率是由动力总成悬置系统的动能和势能推导出的，在具有阻尼的悬置系统中，即使解耦率达到100%，动力总成也不一定达到完全解耦。所以，能量解耦法一般都是在阻尼很小可以忽略时使用[9]。

3.2 基于拉式变换的求解方法

拉普拉斯变换[12]可求一个系统在任何激励下的响应，包括谐波激励和周期激励。这种方法可用于求线性微分方程的精确解，尤其是常系数微分方程。将系统振动微分方程进行拉式变换，得到：

([M]s2+[C]s+[K])X(s)=F(s)

(11)

式中，

F(s)=L(f(t))=∫∞-∞e-stf(t)dt；

X(s)=L(x(t))=∫∞-∞e-stx(t)dt；

其中，s为复数值，称为辅助变量。

[Z(s)]=[M]s2+[C]s+[K]

(12)

(13)

将s换为激励频率p，得到系统响应特性表达式为：

Hij(P)=Xi(p)/Fj(p)

(14)

式中，Hij(P)表示系统在fj(t)激励下，坐标xi的幅频响应特性。

由以上分析可知，利用直接解析法来求解自由度大于2的粘性阻尼受迫振动系统是非常繁琐的，采用拉式变换的方法求解可以简化计算，迅速求得系统的响应特性。

4 计算实例

以某型商用车动力总成为例，其质量1116.5kg。表1为动力总成系统在G0-XYZ坐标系下的转动惯量和惯性积，表2为发动机悬置的位置参数，表3为悬置元件的静刚度。由于橡胶悬置阻尼较小，将系统阻尼比定义在0.1以内。

表1 动力总成系统惯性参数(kg/m2)

表2 悬置点位置参数(mm)

表3 悬置元件各向静刚度值(N/mm)

企业工程师通常采用ADAMS求解系统的解耦率和固有频率，但ADAMS属于专业性较强的动力学分析软件，对于不同型号的发动机需要建立不同的物理模型，并修改相关参数。这样使得整个求解过程步骤繁琐，效率较低，并且对企业工程师软件操作要求较高。

因此，本文基于扭矩轴解耦理论，在考虑阻尼的影响下，利用MATLAB开发了悬置解耦软件，软件操作界面如图3所示。本软件适用于任何型号的发动机，用户只需通过界面输入对应的质量、惯量，悬置位置及刚度、阻尼等参数(也可通过Excel表格自动导入数据)后，点击需要的计算方式(对称计算或者非对称计算)来进行计算，运行结果可以选择用.txt文档进行数据存储，方便用户多次查看。将计算实例的运行结果与ADAMS仿真结果进行对比验证，如表5、表6所示。

图3 软件操作界面

XYZRxRyRz无阻尼8．62776．97769．498010．408513．998317．9908MATLAB8．71926．99019．474810．384313．832817．8401ADAMS8．63926．97789．479710．437513．973117．8992

表6 非比例阻尼条件下MATLAB与ADAMS求解的系统固有频率对比

从上表数据可以看出，无论是存在比例阻尼还是非比例阻尼，MATLAB计算结果与ADAMS仿真结果基本相同，均小于规定误差范围，验证了此软件的正确性。在扭矩轴坐标系下，动力总成的有阻尼系统(包括比例阻尼和非比例阻尼)与无阻尼系统的固有频率不相同，说明阻尼的改变会影响到固有频率的变化。但是因为橡胶悬置自身的动力学特性，阻尼对其固有频率的影响并不是非常明显。

5 结论

本文应用扭矩轴解耦理论，考虑了比例阻尼和非比例阻尼对动力总成悬置系统响应的影响，运用拉式变换进行系统求解，并以固有频率为目标，频率差为约束，开发了计及阻尼影响的MATLAB解耦软件。利用该软件对某型号动力总成悬置系统进行求解，并与ADAMS仿真结果进行对比，结果表明：无论是比例阻尼还是非比例阻尼，对系统的固有频率均有一定的影响。因此，除了合理的配置悬置系统的刚度、位置等参数外，也可通过阻尼的匹配设计来改变系统的固有频率，达到降低共振峰值的目的，为动力总成悬置系统的设计提供了另一种思路。

[1]TaeseokJeong,RauendraSigh.AnalyticalMethodsofDecouplingtheAutomotiveEngineTorqueRollAxis[J].JournalofSoundandVibration,2000,234(1): 85-114.

[2] 靳国才,刘夫云,邓聚才. 汽车动力总成悬置系统的优化研究[J].机械科学与技术,2014,33(2): 271-275.

[3] 范让林,张祥龙. 可变解耦膜刚度半主动液阻悬置研究[J].机械工程学报,2015,51(14):108-114.

[4] 童东红,郝志勇. 基于6σ方法的悬置系统能量解耦与稳健设计[J].汽车工程,2015,37(2): 194-199.

[5] 伍建伟, 刘夫云, 李峤,等. 基于遗传算法汽车动力总成悬置系统解耦优化[J].噪声与振动控制,2015,35(5): 77-81.

[6] 吴杰,上官文斌,唐静,等. 动力总成悬置系统解耦布置的鲁棒性分析[J].振动与冲击,2009,28(9): 15-20.

[7] 付江华,史文库,沈志宏,等. 基于遗传算法的汽车动力总成悬置系统优化研究[J].振动与冲击,2010,29(10): 187-190.

[8] 胡金芳. 计及弹性基础的动力总成悬置系统特性分析与解耦研究[D].合肥:合肥工业大学,2012.

[9] 唐静.动力总成悬置系统动态解耦方法的研究[D].广州:华南理工大学,2010.

[10] 徐铭陶,肖明葵. 工程动力学振动与控制[M]. 北京:机械工业出版社,2004.

[11] 吕兆平. 能量法解耦在动力总成悬置系统优化设计中的运用[J].汽车工程,2008,30(6): 523-526.

[12]SingiresuSRao. 机械振动[M].北京:清华大学出版社,2009.

(编辑 李秀敏)

Decoupling Study of a Powertrain Mounting System with the Effect of Damping

SUNYong-hou1,2,ZHANGJi1,YINShuai1,WANGMeng1

(1.SchoolofMechanicalandElectricalEngineering,GuilinUniversityofElectronicandTechnology,GuilinGuangxi541004,China；2.GuangXiKeyLaboratoryofManufacturingSystem&AdvancedManufacturingTechnology,GuilinGuangxi541004,China)

Tomeetthedemandinlinewiththeactualworkingconditionsofdecoupling,thepaperfacedontheautomotivemountingsystemandconstructtheanalyzemodelofautomobilepowertrainmountingsystem,analyzetheautomobilepowertrainmountingsystemincludethedamping.Andthen,tosolvetheproblemofthedifferentialequationofautomobilepowertrainmountingsystem,theLaplacetransformwasused,calculatethenaturefrequenciesofautomobilepowertrainmountingsystemthatincludeproportionaldampingandnon-proportionaldamping.Atlast,theoptimizedsoftwarewasdevelopedbytheMATLAB,takethevehicleforexample,alsomakinguseofthesoftwarecomparewiththeADAMS.Thenaturefrequenciesofthesoftwarearesame,demonstratesthesoftwareisreliableandthemethodisavailable.

mountingsystem；damping；decoupling

1001-2265(2016)12-0020-03DOI:10.13462/j.cnki.mmtamt.2016.12.006

2016-04-15；

2016-05-03

国家自然科学基金项目(51265006)；广西科技研究与技术开发项目(桂科攻 1348005-11)；广西科技研究与技术开发项目(桂科攻 1598007-51)

孙永厚(1967—)，男，山东沂水人，桂林电子科技大学教授，工学硕士，研究方向为现代设计与制造技术，(E-mail)zyx881123@163.com。

TH164;TG

A