从效应量应有的性质看中介效应量的合理性*

温忠麟范息涛叶宝娟陈宇帅

(1华南师范大学心理应用研究中心/心理学院,广州 510631)(2澳门大学,澳门)(3江西师范大学心理学院,南昌 330022)

国际上对心理学和其他社科领域的方法研究有重要影响的期刊Psychological Methods(2014年影响因子7.34)发表了Preacher和Kelley(2011)的论文讨论中介效应量,经过一番评长论短,对当时已有的中介效应量都有不满,最终推荐的是他们新提出的κ作为中介效应量。从此κ在国际上流行开来,不仅有论著介绍(Athay,2012;方杰,张敏强,邱皓政,2012;Field,2013),而且有许多实际应用(例如,Koletzko,Herrmann,&Brandstätter,2015;Labelle,Lawlor-Savage,Campbell,Faris,&Carlson,2015;Rivera&Fincham,2015),在互联网上也有κ的计算器(如http://stats.myresearchsurvey.com/kappasquared/),很方便使用。然而,Wen和Fan(2015)通过逻辑判断和数学推演,证明了κ不仅计算错误,而且从定义开始就有问题。他们的研究结果终结了κ作为中介效应量的合法性。κ的问题出在哪里、又是如何被发现的？这要从效应量的作用和性质寻找答案。本文首先介绍效应量的相关知识,如何根据统计显著性和效应量作出统计结论;接着讨论效应量应当具有哪些基本性质;然后根据这些性质检视包括κ在内的主要中介效应量的合理性;最后,讨论了如何报告中介效应量以及有待研究的问题。

1 效应与效应量

1.1 显著性检验不能满足需要

尽管争论不断,零假设显著性检验(NHST)仍然是大多数统计分析不可或缺的重要环节,至少“显著性”的结果能告诉我们,效应(effect)不太可能是由样本的抽样误差而产生的,提高了对研究假设(即备择假设

H

)的信心(温忠麟,吴艳,2010)。不过,单单一个“显著性”的结果,所得结论是很弱的。以通常的两组差异检验为例,差异显著说明“差异在统计上可以分辨出来”,但并没有指出差异有多大(温忠麟,侯杰泰,2008)。再以相关分析为例,相关显著说明“相关系数不是零”,但并没有指出相关有多高。这就不难理解,诸如检验测验信度系数(如重测信度)的显著性那样的统计分析是没有意义的,因为人们感兴趣的是“信度有多高”,而不是“信度是否为零”。

为了弥补显著性检验的不足,在统计分析结果中报告效应量(effect size)受到重视(Fan&Konold,2010;Thompson,2007;Wilkinson,1999),不仅多数国际期刊要求报告效应量,国内不少重要期刊也要求报告效应量。

1.2 效应通常缺少可比性

研究者不满足于效应显著与否,还想知道效应有多大。每种统计分析都会有一个或多个我们感兴趣的量,称为效应。例如,通常的两组差异分析,效应是两组均值差异;在一元回归分析中,效应是回归系数,反映了当自变量变化一个单位时,因变量变化了多少个单位;方差分析中,感兴趣的效应可能包括因素的主效应和交互效应,通常由效应平方和来衡量。

任何一个效应本身就是一个数量,如果涉及的变量有公认的量尺和测量单位,如长度测量使用米尺、抽烟数量以每天抽烟支数计算,则效应本身就是现成的效应量。例如,“男女身高均值差异为0.1米”、“男员工比女员工平均每天多抽2.5支烟”,意义就相当明确,同类的不同研究之间也有可比性。而且,这个基于原始测量单位的效应量与其他变换后的各种效应量相比,不仅简单,而且更加容易理解。

在物理测量中,通常都有公认的测量单位,就算测量单位不同,也可以彼此等值转换(如1米 =100厘米)。然而,心理测量通常不像物理测量那样有通行世界的公制单位,不同的测量之间也难以等值转换。因为不同的研究可能使用不同的量表,有不同的测量单位,所以基于原始测量单位的效应缺少可比性。例如,研究一项英语培训方法的效果,有研究者用雅思(IELTS)测试成绩,发现培训后平均增加了1.2分;另有研究者用托福(TOEFL)测试成绩,发现培训后平均增加了9.5分。这时,既不知道IELTS提高1.2分或者TOEFL提高9.5分算是效应高还是低,也不知道两个研究者的培训效应谁的较高。这时,需要一种与测量单位无关(scale-free)的指标——效应量,来衡量效应的大小。

1.3 常见效应量

这里我们回顾一下常见统计方法的效应量,方便后面引用。在两组差异分析中,最常用的效应量是Cohen(1988,p.67)的d：

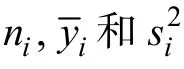
在一元回归分析中,最常用的效应量是复相关系数平方(squared multiple correlation coefficient)R(Cohen,Cohen,West,&Aiken,2003)：

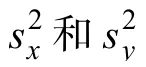
在方差分析(ANOVA)中,最常用的效应量是η(Cohen,1973;Olejnik&Algina,2000):

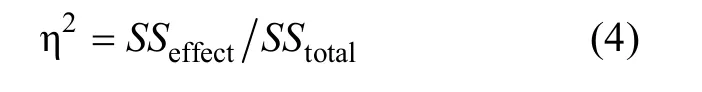
其中SS是感兴趣的效应平方和,SS是总平方和。

2 效应量与效应的显著性

给定显著性水平(通常是0.05),对一个效应检验结果要么显著,要么不显著。先看效应不显著的情形：

(1)如果效应量小,说明效应既无统计意义也无实际意义,通常都可以认为效应不存在。

(2)如果效应量达中上大小,需要看检验力高低,如果检验力高,可以认为效应是由抽样误差引起;否则还不能下结论,应当增加被试提高检验力,重新做统计分析。一般地说,对于中等以上的效应量,只要样本容量足够大(因而检验力足够高),效应都会显著。

再看效应显著的情形：

(1)如果效应量小,除非有理由说明小的效应量也会引起严重后果,否则通常都认为没有实际意义。就是说,效应量小的时候,显著也没有实际意义。

(2)如果效应量达中上大小,已经有理据做出结论,效应在统计上和实际上都有意义。

效应量多大算小、中或大,要看具体的效应量是什么,在不同的研究领域通常会有约定俗成的大致标准。例如Cohen(1969)提出,d=0.2、d=0.5和d=0.8分别对应于小、中、大的效应量,是心理学科很多人引用的标准。不同研究可能考虑的效应量可参考郑昊敏、温忠麟和吴艳(2011)的文章。有关检验力与效应量、样本容量的关系,可参考吴艳和温忠麟(2011)的文章。

表1总结了如何根据检验的统计显著性与效应量得出统计结论。不论检验结果是否显著,计算和报告效应量总是需要的,结合显著性和效应量才能得到适当的统计结论。但并不是任何时候都要考虑检验力。当检验结果是显著时,不用考虑检验力高 低,因为此时可能犯的错误是第一类错误。只有当检验结果是不显著时,才需要考虑检验力(相当于报告第二类错误率)。不过,如果效应量小,通常都没有必要看检验力高低,可以直接作出没有效应的结论;如果效应量中上,检验不显著会令人怀疑是检验力不够高所致,文章投稿难以被接受,此时适当增加样本容量,通常都会得到显著结果。所以,虽然研究者需要有检验力的概念,知道增加样本容量是提高检验力的途径,但是可以说在文章中是不必报告检验力的。

表1 根据统计显著性和效应量作出统计结论

3 效应量应当有的性质

一个统计量应当具有哪些性质才能成为一个效应量呢？目前似乎未见有文献做专门的讨论,尽管Kelley和Preacher(2012)在极其宽泛的效应量定义下,提到了好的效应量应当有的性质(也见Preacher&Kelley,2011)。他们说的性质是针对一个效应量好不好而言,而本文说的效应量应当有的性质,是针对一个统计量能不能作为效应量而言。这里我们尝试从引入效应量的动机和效应量的作用思考效应量应当有的性质。

3.1 与测量单位无关

在基于原始测量单位的效应之外,还要引入效应量的一个动机是避免测量单位的影响,所以,“与测量单位无关”应当是效应量的重要性质,缺少这个性质的效应量就算被定义出来,迟早会被别的有这个性质的效应量取代。

怎样知道一个效应量与测量单位无关呢？如果一个效应量用原始分数和Z分数(与测量单位无关)计算结果相同,那么这个效应量就与测量单位无关。有两种做法都可以产生与测量单位无关的效应量,一种做法是对效应进行标准化,Cohen的

d

属于这一种。另一种做法是将效应量定义为一种比例,回归分析和方差分析中的效应量属于这一种。

3.2 相对于效应而言具有单调性

效应量是用来衡量效应的大小的,如果保持其他条件不变,效应(绝对值)越大,效应量(绝对值)也应当越大。就是说,相对于效应而言,效应量应当具有单调性(monotonicity)。缺乏了这个性质的效应量会难以理解,也不符合逻辑。所以单调性是一个效应量应当有的性质。

如何判断一个效应量具有单调性呢？如果一个效应量与效应(研究者感兴趣的量)成正比,那么该效应量有单调性。一般地,如果一个效应量(绝对值)是效应(绝对值)的单调上升函数,那么该效应量有单调性,下面看几个例子(Wen&Fan,2015)。

在回归分析中,当

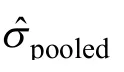
s

和

s

保持不变时,由公式(3)可知,

R

是|

b

|(

b

与–

b

效应相同,方向相反)的单调上升函数,所以,效应量

R

有单调性。在方差分析中,当总平方和

SS

保持不变时,由公式(4)可知η显然与

SS

成正比,所以η有单调性。

3.3 不受样本容量的影响

此处所说的影响是指系统影响。设想一下,如果一个统计量会随着样本容量的增加而不断增大(或减小),或者波动起伏太大,那么这样的统计量难以衡量效应大小,不能作为效应量。根据定义,统计量都难免与样本容量有关系,连简单的样本均值和样本方差都不例外。但样本均值和样本方差分别是总体均值和总体方差的无偏估计,随着样本容量的增加,它们分别在总体均值和总体方差附近波动,不受样本容量的影响(independent of sample size)。但有的统计量会系统地受到样本容量的影响,例如两组差异分析,独立样本的

t

检验统计量为

为两个样本的混合标准差。

t

统计量受到样本容量的影响。为了容易理解,看看

n

=

n

=

n

的特殊情形,此时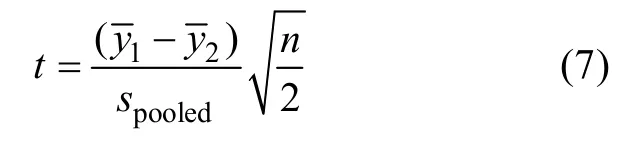

可见随着样本容量的增加,

t

会系统地变大,只要被试人数足够多,很小的差异都会得到显著性结果,这是很多读者都知道的事实。因此,

t

不能作为效应量,这是在有了与测量单位无关的

t

值后,还要定义和报告效应量的原因。怎么知道一个效应量不受样本容量的影响呢？以

d

为例,一方面是通过统计知识可以推理出来,因为由公式(1)可知,分子是两组均值之差,分母是总体的混合标准差的估计,都不受样本容量的影响。另一方面是大量的经验可以知道,

d

不像

t

那样会随着样本的增加而系统地变大。在回归分析中,

R

作为相关系数的平方,不受样本容量的影响。在方差分析中,η可以由统计量

F

转换得到(Cohen,1965)：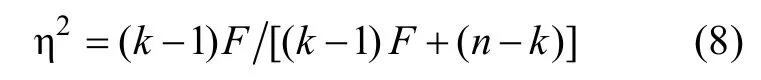

其中

k

是组数,

n

是各组被试总和,

F

的自由度是(

k

–1,

n

–

k

)。大量经验告诉我们,η不受样本容量的影响。

3.4 效应量的其他性质

除了上面讨论的效应量应当有的性质外,还可以考虑是否有如下性质：非负性、有界性和正规性。如果一个效应量是非负的数,则该效应量有非负性。如果一个效应量的绝对值有界,则该效应量有有界性。如果一个效应量取值范围在[0,1]上,则该效应量有正规性。显然,回归分析中的

R

和方差分析中的η都有非负性、有界性和正规性,但差异分析中的效应量

d

有可能是负值、也可能无界、更没有正规性。考虑到非负的效应量容易理解,在不考虑效应的方向或者将方向另外考虑后,总可以将效应量定义为非负值,一个简单的方法是只考虑效应量的绝对值,这也是通常默认的做法,例如Cohen(1969)提出,

d

=0.2、

d

=0.5和

d=

0.8分别对应于小、中、大的效应量,显然只是考虑绝对值。只要一个效应量有有界性,总可以通过一个线性变换将其变到[0,1]上,成为有规范性的效应量。但效应量

d

做不到这一点,因为它是无界的。

4 中介模型和常用中介效应量

4.1 中介模型简介

考虑自变量

X

对因变量

Y

的影响,如果

X

通过影响变量

M

而对

Y

产生影响,则称

M

为中介变量(Baron&Kenny,1986;Judd&Kenny,1981;温忠麟,叶宝娟,2014)。为了简便起见,假设所有变量都已经中心化(均值为0)或者标准化(均值为0,标准差为1),可用下列回归方程来描述变量之间的关系(图1是相应的路径图)：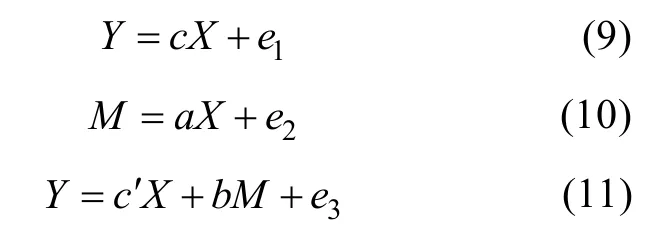

其中方程(9)的系数

c

为自变量

X

对因变量

Y

的总效应;方程(10)的系数

a

为自变量

X

对中介变量

M

的效应;方程(11)的系数

b

是在控制了自变量

X

的影响后,中介变量

M

对因变量

Y

的效应;系数

c

¢是在控制了中介变量

M

的影响后,自变量

X

对因变量

Y

的直接效应;

e

～

e

是回归残差。对于这样的简单中介模型,中介效应等于间接效应(indirect effect),即等于系数乘积

ab

,它与总效应和直接效应有下面关系(MacKinnon,Warsi,&Dwyer,1995)：

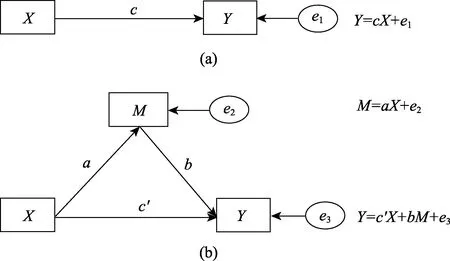
图1 中介模型示意图

4.2 常用中介效应量及其性质

在中介分析中,研究者感兴趣的中介效应就是间接效应

ab

。最常用的中介效应量是间接效应占总效应的比例(Alwin&Hauser,1975;MacKinnon,2008;MacKinnon&Dwyer,1993;Preacher&Kelley,2011)：

通过将所有变量做标准化变换,不难验证

P

与测量单位无关。因为

P

只涉及回归系数,所以不会受到样本容量的影响。如果只考虑绝对值,当总效应

c

固定时,

P

与

ab

成正比,因而有单调性。传统中介模型中,间接效应

ab

与直接效应

c

¢有相同的符号(即所谓的一致中介模型,consistent mediation model),因而都与总效应有相同的符号,此时

P

不仅有界,还是正规的,取值在[0,1]上。对于不一致中介模型(inconsistent mediation model,MacKinnon,Krull,&Lockwood,2000),间接效应

ab

与直接效应

c

¢有相反的符号,此时

P

虽然还是有单调性,但是无界的(Preacher&Kelley,2011)。顺便说明一下,有文献将一致中介模型称为互补中介模型(complementary mediation),而将不一致中介模型称为竞争中介模型(competitive mediation models,Zhao,Lynch,&Chen 2010)。

另一个简单的中介效应量是间接效应与直接效应之比 (MacKinnon,2008;Preacher&Kelley,2011;Sobel,1982):和

P

一样的是,

R

也与测量单位无关,而且不会受到样本容量的影响。不同的是,

R

只对传统中介模型有单调性。在传统中介模型中,不妨假设所有系数都是非负的,当总效应固定时,由

c

=

ab

+

c

¢可知,随着

ab

的上升,

c

¢下降,因而

R

是

ab

的单调上升函数。但对于不一致中介模型,

R

没有单调性。例如,假设给定

c

=0.3,当

ab

分别等于–0.2,0.4和0.6时,对应的

c

¢分别等于0.5,–0.1和–0.3, 结果是

R

分别为–0.4,–4,–2。所以当总效应固定时(

c

=0.3),无论是

R

还是其绝对值,都不是

ab

的单调函数(Wen&Fan,2015)。不难看出,无论是传统的中介模型还是不一致中介模型,

R

都是无界的。

5 中介效应量κ2的问题

5.1 κ2的定义和性质

Preacher和Kelley(2011)对当时已有的中介效应量做了回顾,并讨论了它们的性质,发现已有的中介效应量都存在不足。他们在文中新提出了两个中介效应量,一个是基于残差定义的指标,用于衡量中介变量(

M

)和结果变量(

Y

)的变异解释率。但这个指标相当复杂,他们最后并未推荐,而是建议作为补充指标使用。另一个是κ,定义为间接效应与间接效应的最大可能值之比：

这个最大可能值

m

(

ab

)是在给定总效应

c

后,在

X

、

M

和

Y

的相关矩阵是非负定的条件下,间接效应

ab

的最大值。κ是他们最终推荐使用的中介效应量,具有如下性质：(i)非负,(ii)取值在[0,1]上,(iii)与测量单位无关,(iv)可以构造bootstrap置信区间,(v)不受样本容量的影响(Preacher&Kelley,2011)。

5.2 κ2缺乏单调性

细心的读者或许已经注意到,上面列出的κ的多个性质中,缺少了重要的单调性。Wen和Fan(2015)正是通过考察κ的单调性发现它有问题。为了展示κ没有单调性,他们使用两个数据例子。

在第一个例子中,固定总效应为

c

=0.190,

a

=0.291,

b

=0.478,

c

¢= 0.051,

ab

=(0.291)(0.478)=0.139,κ=0.143。在第二个例子中,还是固定总效应为

c

=0.190,

a

=0.250,

b

= 0.545,

c

¢=0.054,

a

b

=(0.250)(0.545)=0.136,κ=0.146(Wen&Fan,2015)。上面两个数据例子中的总效应相同,都是0.190。但当中介效应

ab

从0.139降到0.136时,κ却从0.143升至0.146。这说明,κ没有单调性。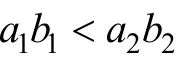

5.3 κ2没有单调性的原因

按理说,

m

(

ab

)是满足某种条件下的最大值,是与

a

无关且与

b

也无关的一个常数,因而κ应当与

ab

成正比。为什么κ没有单调性呢？Wen和Fan(2015)发现,问题出在Preacher和Kelley(2011)错误地用

m

(

ab

)=

m

(

a

)

m

(

b

)来计算

m

(

ab

),其中

m

(

a

)是给定

c

和

b

后系数

a

的最大值;

m

(

b

)是给定

c

和

a

后系数

b

的最大值。因而,在给定

c

后,

m

(

a

)与

b

有关,而

m

(

b

)与

a

有关,结果是

m

(

a

)

m

(

b

)与

a

和

b

都有关,说明

m

(

ab

)=

m

(

a

)

m

(

b

)是不成立的。随着

ab

的上升,

m

(

a

)

m

(

b

)可能上升也可能下降,导致κ没有单调性。Wen和Fan给出一个简单的数据例子,用来说明为什么κ没有单调性。

5.4 κ2的定义不当

既然

m

(

ab

)=

m

(

a

)

m

(

b

)不成立,那么

m

(

ab

)该如何计算？Wen和Fan(2015)用初等代数证明了

m

(

ab

)其实是无穷大(可以理解为比任何一个正整数都大),这一点肯定出乎Preacher和Kelley(2011)的意外。因为任何数除以无穷大等于0,所以κ的定义本身就有问题,就是说,在定义中将

m

(

ab

)用来做分母是不对的。

6 R2型中介效应量的问题

前面的讨论说明,Preacher和Kelley(2011)提出的κ该彻底停用了。我们只好回头看看其他中介效应量。检视文献上出现的中介效应量,除了传统的中介效应量

P

外,值得考虑的是

R

型中介效应量,其他一些定义复杂、计算繁琐、解释困难的中介效应量则不拟涉及。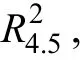

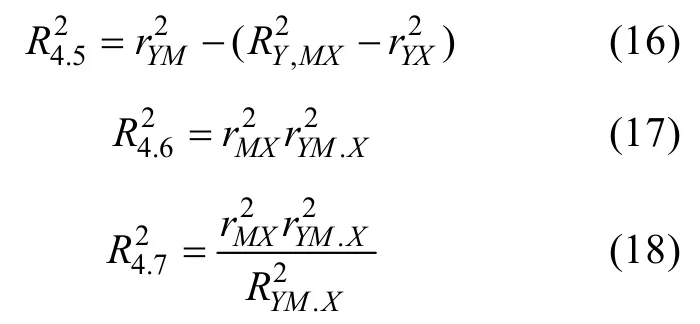
其中

r

表示

Y

与

M

的相关系数(平方后就是

Y

的方差被

M

解释的比例),

R

表示

Y

对

X

和

M

的回归(11)得到的

R

(即

Y

的方差被

X

和

M

解释的比例),

r

表示在消除了

X

影响后

Y

与

M

的偏相关(partial correlation)系数。De Heus(2012)提出了改良版的

R

,将偏相关系数

r

用部分相关(part4.6correlation)系数

r

代替：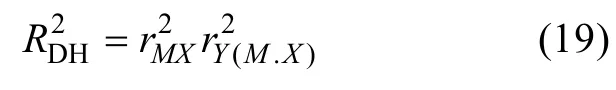

但是,上面几个

R

型中介效应量全部都没有单调性(Lachowicz,2015;Wen&Fan,2015),并且也不像

R

那样可以理解为方差被解释的比例(Lachowicz,2015;Preacher&Kelley,2011)。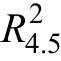

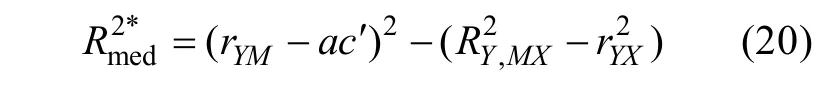
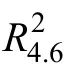
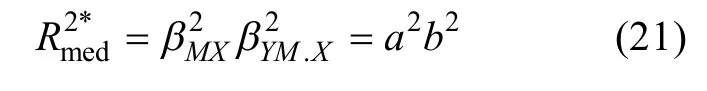
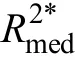
在一元回归分析中,将标准化回归系数(就是相关系数

r

)平方后(就是

R

)作为效应量,就是因变量的方差被解释的比例,有明确的统计意义并且方便推广到多个自变量的情形。但现在将中介效应进行平方,解释上已经成问题,推广到多重中介模型更加难以解释,还不如直接使用标准化的中介效应大小容易解释和推广。

7 同时报告多个指标对中介效应做出评价

究竟应当如何报告中介效应量呢？传统的中介效应量

P

有单调性,但如果仅仅报告

P

其实反映不出来中介效应的大小。例如,如果一个研究的总效应

c

=0.6,另一个研究的总效应

c

=0.3,那么同样都是

P

=0.5,前一个研究的中介效应比后一个研究的强多了。所以,单单看一个

P

,研究之间缺少可比性。另一个常见的中介效应量

R

没有单调性,所以不建议用作中介效应量,但作为一个统计结果还是可以报告的,让读者了解间接效应与直接效应的相对大小。可以说没有一个现有的中介效应量能令人满意,或者说,没有哪个单个的中介效应量能担当衡量中介效应大小的作用。那该如何报告中介效应量呢？Wen和Fan(2015)的建议是同时报告多个统计量。首先应当同时报告总效应的原始估计(如果有意义)和标准化估计(与测量单位无关)。前者反映了当

X

变化一个单位时,

Y

将变化多少个单位。后者反映了当

X

变化一个标准差时,

Y

将变化多少个标准差。然后报告间接效应

ab

和直接效应

c

¢的原始估计和标准化估计。当

ab

和

c

¢符号一致时,报告

P

是有意义的,说明了中介效应占总效应的比例。例如,如果

c

=0.5,间接效应

ab

=0.2,直接效应

c

¢=0.3(都是标准化估计),可以做如下解释：当

X

变化一个标准差时,

Y

将变化0.5个标准差,其中0.2是

X

通过中介变量

M

对

Y

起作用,而余下的0.3则是

X

直接对

Y

起作用。中介效应占了总效应的40%(=0.2/0.5)。上述这些统计量,不仅容易计算,而且容易解释。总之,只要

ab

和

c

¢符号一致(此时

ab

不超过总效应

c

),事情就好办,在有了标准化估计的

ab

和中介效应量

P

后,中介效应的绝对大小和相对大小都已经明确了。对于不一致的中介模型(

ab

和

c

¢符号相反),标准化估计的

ab

是没有界的,

P

也没有界。此时,无论看着标准化估计的

ab

还是中介效应量

P

,对中介效应大小可能都没有谱,不知道多少算大,多少算小。或许通过同类研究的元分析,可以提供中介效应大小幅度的一个参照系(Wen&Fan,2015)。除了报告标准化估计的

ab

和

P

外,是否还有什么指标可用来作为中介效应量呢？如果有,是否也可以作为不一致的中介模型的中介效应量？都是有待研究的问题。Alwin,D.F.,&Hauser,R.M.(1975).The decomposition of effects in path analysis.

American Sociological Review,40

,37–47.Athay,M.M.(2012).Satisfaction with Life Scale(SWLS)in caregivers of clinically-referred youth: Psychometric properties and mediation analysis.

Administrationand PolicyinMentalHealthandMentalHealthServices Research,39

,41–50.Baron,R.M.,& Kenny,D.A.(1986).The moderator–mediator variable distinction in social psychological research:Conceptual,strategic,and statistical considerations.

Journal of Personality and Social Psychology,51

,1173–1182.Cohen,J.(1965).Some statistical issues in psychological research.In B.B.Wolman(Ed.),

Handbook of clinical psychology

.New York:McGraw-Hill.Cohen,J.(1969).

Statistical power analysis for the behavioral sciences

.New York:Academic Press.Cohen,J.(1973).Eta-squared and partial eta-squared in fixed factor ANOVA designs.

Educational and Psychological Measurement,33

,107–112.Cohen,J.(1988).

Statistical power analysis for the behavioral sciences

(2nd ed.).New York:Erlbaum.Cohen,J.,Cohen,P.,West,S.G.,&Aiken,L.S.(2003).

Applied multiple regression/correlation analysis for the behavioralsciences

(3rd ed.)

.

Mahwah,New Jersey:Lawrence Erlbaum Associates,Inc.De Heus,P.(2012).R squared effect-size measures and overlap between direct and indirect effect in mediation analysis.

Behavior Research Methods,44

,213–221.Fairchild,A.J.,Mackinnon,D.P.,Taborga,M.P.,&Taylor,A.B.(2009).

R

effect-size measures for mediation analysis.

Behavior Research Methods,41

,486–498.Fan,X.,&Konold,T.R.(2010).Statistical significance versus effect size.In P.Peterson,E.Baker,and B.McGaw(Eds.),

International encyclopedia of education

(3rd ed.,Vol.7,pp.444–450).Oxford:Elsevier.Fang,J.,Zhang,M.Q.,&Chiou,H.J.(2012).Mediation analysisand effectsize measurement:Retrospectand prospect.

Psychological Development and Education,28

,105–111.[方杰,张敏强,邱皓政.(2012).中介效应的检验方法和效果量测量:回顾与展望.

心理发展与教育,28

,105–111.]Field,A.(2013).

Discovering statisticsusing IBMSPSS statistics

(pp.408–419).London:SAGE.Judd,C.M.,& Kenny,D.A.(1981).Processanalysis:Estimating mediation in treatment evaluations.

Evaluation Review,5

,602–619.Kelley,K.,& Preacher,K.J.(2012).On effectsize.

Psychological Methods,17

,137–152.Koletzko,S.H.,Herrmann,M.,&Brandstätter,V.(2015).Unconflicted goal striving:Goal ambivalence as a mediator between goal self-concordance and well-being.

Personality and Social Psychology Bulletin,41

,140–156.Labelle,L.E.,Lawlor-Savage,L.,Campbell,T.S.,Faris,P.,&Carlson,L.E.(2015).Does self-report mindfulness mediate the effect of Mindfulness-Based Stress Reduction(MBSR)on spirituality and posttraumatic growth in cancer patients?.

The Journal of Positive Psychology,10

,153–166.Lachowicz,M.(2015).

A novel measure of effect size for mediationanalysis

(Unpublished master's thesis).Vanderbilt University.MacKinnon,D.P.(2008).

Introduction to statistical mediation analysis.

Mahwah,NJ:Erlbaum.MacKinnon,D.P.,& Dwyer,J.H.(1993).Estimating mediated effects in prevention studies.

Evaluation Review,17

,144–158.MacKinnon,D.P.,Krull,J.L.,&Lockwood,C.M.(2000).Equivalence of the mediation,confounding and suppression effect.

Prevention Science,1

,173–181.MacKinnon,D.P.,Warsi,G.,&Dwyer,J.H.(1995).A simulation study of mediated effect measures.

Multivariate Behavioral Research,30

,41–62.Olejnik,S.,&Algina,J.(2000).Measures of effect size for comparative studies:Applications,interpretations,and limitations.

Contemporary Educational Psychology,25

,241–286.Preacher,K J.,&Kelley,K.(2011).Effect size measures for mediation models:Quantitative strategies for communicating indirect effects.

Psychological Methods

,

16

,93–115.Rivera,P.M.,& Fincham,F.(2015).Forgivenessas a mediator of the intergenerational transmission of violence.

Journal of Interpersonal Violence,30

,895–910.Sobel,M.E.(1982).Asymptotic confidence intervals for indirecteffects in structuralequation models.In S.Leinhardt(Ed.),

Sociological methodology

(pp.290–312).Washington,DC:American Sociological Association.Thompson,B.(2007).Effect sizes,confidence intervals,and confidence intervals for effect sizes.

Psychology in the Schools,44

,423–432.Wen,Z.,&Fan,X.(2015).Monotonicity of effect sizes:Questioning kappa-squared as mediation effect size measure.

Psychological Methods,20

,193–203.Wen,Z.,&Hau,K.-T.(2008).Cutoff values for testing:How great the difference between the true and the false makes them distinguishable?

Acta Psychologica Sinica,40

,119–124.[温忠麟,侯杰泰.(2008).检验的临界值:真伪差距多大才能辨别?

心理学报,40

,119–124.]Wen,Z.,&Wu,Y.(2010).Misuses and misunderstandings in statistics by psychologists.

Journal of South China Normal University(Social Science Edition),

(1),47–54.[温忠麟,吴艳.(2010).屡遭误用和错批的心理统计.

华南师范大学学报(社会科学版),

(1),47–54.]Wen,Z.,&Ye,B.(2014).Analyses of mediating effects:The development of methods and models.

Advancesin Psychological Science,22

,731–745.[温忠麟,叶宝娟.(2014).中介效应分析:方法和模型发展.

心理科学进展,22

,731–745.]Wilkinson,L.(1999).Statistical methods in psychology journals:Guidelines and explanations

.American Psychologist,54

,594–604.Wu,Y.,&Wen,Z.(2011).The statistical analysis procedure involving null hypothesis significance testing.

Psychological Science,34

,230–234.[吴艳,温忠麟.(2011).与零假设检验有关的统计分析流程.

心理科学,34

,230–234.]Zhao,X.,Lynch,J.G.,&Chen,Q.(2010).Reconsidering Baron and Kenny:Mythsand truthsaboutmediation analysis.

Journal of Consumer Research,37

,197–206.Zheng,H.,Wen,Z.,&Wu,Y.(2011).The appropriate effect sizes and theircalculationsin psychologicalresearch.

Advances in Psychological Science,19

,1868–1878.[郑昊敏,温忠麟,吴艳.(2011).心理学常用效应量的选用与分析.

心理科学进展,19

,1868–1878.]