三次B样条曲线形状调整方法

王晶昕，鞠　妍

(辽宁师范大学数学学院，辽宁 大连 116029)



三次B样条曲线形状调整方法

王晶昕，鞠妍

(辽宁师范大学数学学院，辽宁 大连 116029)

摘要：分析了某种带局部形状调整参数的B样条曲线的构造,提出用带调整参数的变换矩阵方法生成控制点进而生成所要求的带形状参数的三次B样条曲线的方法.研究了参数变化对曲线的影响,以及该方法下所生成样条曲线在拼接点处的连续性条件.

关键词：三次B样条曲线;调整参数;矩阵变换

在B样条曲线的形状调整的研究中有很多行之有效的方法[1-4].文献[1]中构造出了一种新的三次、四次调配函数,以此作为三次B样条基函数的扩展,通过改变局部形状参数达到对曲线形状调整的目的.笔者对文献[1]中所给出的方法进行分析,试图找出这种调配函数生成的曲线与标准的B样条基函数生成的曲线之间的联系与区别.经分析发现,如果将给定的控制点进行某种方式的凸组合生成新的控制点,那么仅利用标准的B样条基函数即可生成文献[1]中的方法所生成的曲线.此外，还可以用上述控制点的更一般化的凸组合来生成新的控制点,从而生成自由度更大的B样条曲线.而这种方法生成的B样条曲线在拼接点处的连续性依赖于上述组合系数的选择.

1对扩展三次B样条曲线的分析

因为样条曲线即是分片的多项式曲线,所以笔者沿用文献[1]中的方法,讨论一个样条区间中的多项式曲线,再分析相邻的下一段多项式曲线与之拼接的问题即可.

文献[1]中带形状参数λi的第1类三次B样条的扩展基在第i个区间的函数表示为

(1)

其中t∈[0,1],-2≤λi≤1.

对(1)式进一步变形得

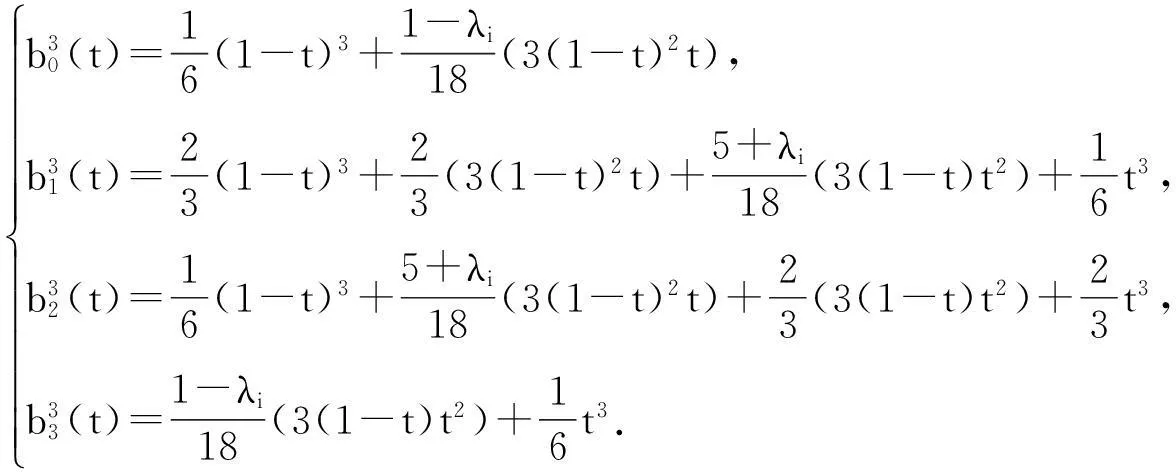
(2)

取定4个控制点P0,P1,P2,P3,得多项式曲线

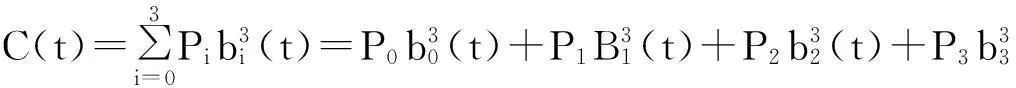
(3)

将(2)式代入(3)式后整理得

即

记

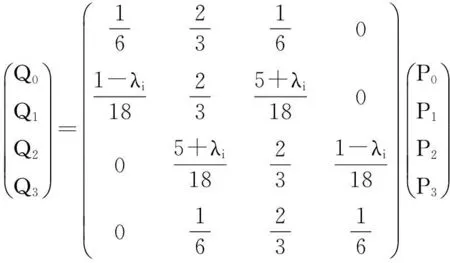
(4)

(5)

如图1为λi=0的情形.

对文献[1]中带形状参数λi的第2类四次B样条扩展基做同样分析:

图1　λi=0

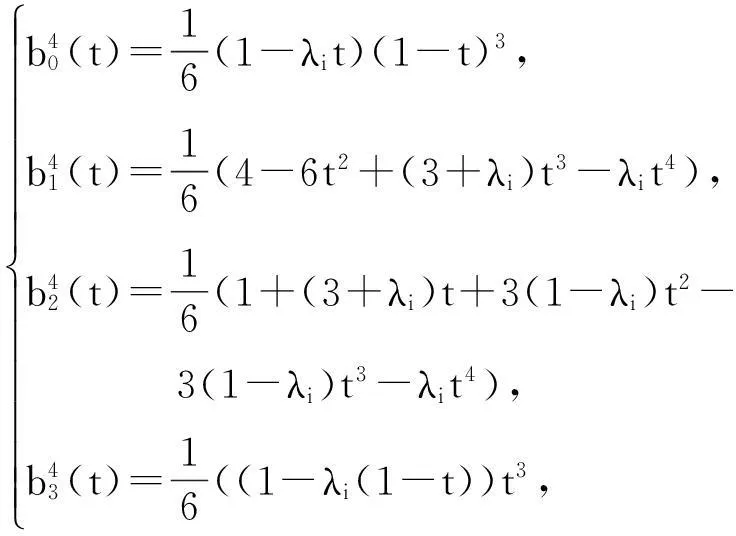
(6)

其中t∈[0,1],-2≤λi≤1.

对(6)式作进一步变形,最后得到曲线C(t)也可用控制点Qi(i=0,1,2,3,4)与标准的四次Bernstein基函数表示出来,即

记

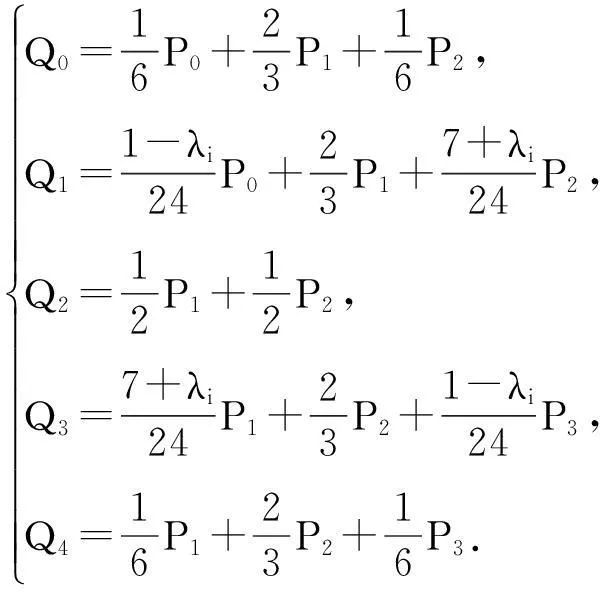
同样Q0,Q1是3个控制点P0,P1,P2的凸组合,Q2是P1,P2的凸组合,Q3,Q4是P1,P2,P3的凸组合.按这个方法邻接于点Q3处的下一段曲线的控制点是

图2　λi=1

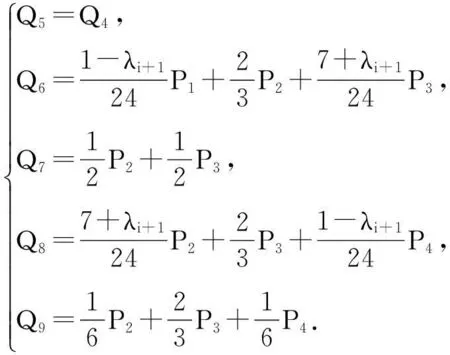
如图2为λi=1的情形.

2构造带调整参数的三次B样条曲线

对上一节的分析作进一步探索,又可以发现新问题:既然Q0,Q1,Q2,Q3是原控制点的凸组合,而组合系数仅受一个参数λi制约,那么采用多个组合系数生成新控制点是不是可以得到自由度更大的样条曲线？如果要求这样生成的分片曲线在拼接点处达到一定的连续性,本段曲线所选取的参数与下一段曲线选取的参数之间应该满足什么样的条件？这就是本节要讨论的问题.

对于任意给定4个控制顶点P0,P1,P2,P3,作变换

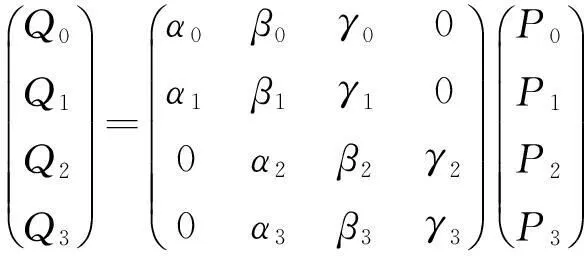
即为

其中αi,βi,γi∈[0,1],文中这类参数均满足αi+βi+γi=1的关系.

考察曲线

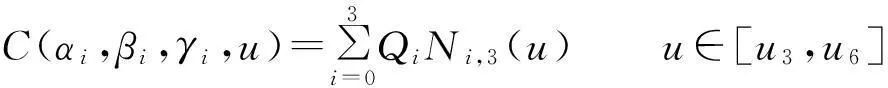
它是由顺次以Q0,Q1,Q2,Q3为控制点的Bézier曲线,若与之在点Q3处相连接的下一段Bézier曲线的控制点是

设以Q0,Q1,Q2,Q3为控制点的Bézier曲线为C1,以Q4,Q5,Q6,Q7为控制点的Bézier曲线为C2.显然,若仅要求C1与C2在拼接点处达到G0连续,则只要C1(1)=C2(0),即Q4=Q3即可.但若要求C1与C2在拼接点处达到更高阶的连续性,则需要所选择的参数之间满足更多的条件.

引理1[5]2段Bézier曲线在连接点处达到G1连续的充分条件为:

(ⅰ)在连接点处重合,即C1(1)=C2(0);

引理2[5]2段Bézier曲线在连接点处达到G2连续的充分条件为:

(ⅰ)在连接点处G1连续；

由上述引理可以推知下面的结果:

定理1若相邻2段曲线C1与C2的形状参数满足α4=α3,β4=β3,γ4=γ3,则此二曲线C1与C2在拼接点处达到G0连续.

定理2若相邻2段曲线C1与C2的形状参数满足如下2个条件,则此二曲线C1与C2在拼接点处达到G1连续:

(ⅰ)(α4,β4,γ4)=(α3,β3,γ3);

(ⅱ)存在K>0,使得(α5,β5,γ5)=(1+K)(α3,β3,γ3)-K(α2,β2,γ2).

α5P1+β5P2+γ5P3=(1+K)(α3P1+β3P2+γ3P3)-K(α2P1+β2P2+γ2P3).

由此求得

α5=(1+K)α3-Kα2,β5=(1+K)β3-Kβ2.

进而可计算出

γ5=(1+K)γ3-Kγ2=(1+K)(1-α3-β3)-K(1-α2-β2)=(-(1+K)α3+Kα2)+

(-(1+K)β3+Kβ2)+1=1-α5-β5.

故可知定理2结论成立.

容易计算,文献[1]中的第1类曲线所对应的变换(4),(5)满足定理2的条件,故所产生的新的曲线在连接点处是G1连续的.

对文献[1]中的第2类曲线作对应的变换:

(7)

(8)

为讨论相邻2段曲线C1与C2在连接点处的G2连续性,先作一些分析.

首先，若要C1与C2在连接点处是G1连续的，只要有:

(1)(α5,β5,γ5)=(α4,β4,γ4);

(2)存在K>0,使得(α6,β6,γ6)=(1+K)(α4,β4,γ4)-K(α3,β3,γ3).

这样,(8)式应为

(9)

计算可知

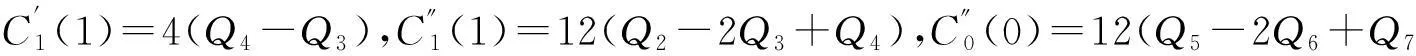
12(Q5-2Q6+Q7)=12L(Q2-2Q3+Q4)+4υ(Q4-Q3),

Q5-2Q6+Q7=L(Q2-2Q3+Q4)+υ(Q4-Q3),

Q5-2((1+K)Q4-KQ3)+Q7=L(Q2-2Q3+Q4)+υ(Q4-Q3).

将(8),(9)式代入得

(α5P1+β5P2+γ5P3)-2(1+K)(α4P1+β4P2+γ4P3)+2K(α3P1+β3P2+γ3P3)+

(α7P2+β7P3)=L((α2P1+β2P2)-2(α3P1+β3P2+γ3P3)+(α4P1+

β4P2+γ4P3))+υ((α4P1+β4P2+γ4P3)-(α3P1+β3P2+γ3P3))·

(2Kα3-(1+2K)α4)P1+(2Kβ3-(1+2K)β4+α7)P2+

(2Kγ3-(1+2K)2γ4+β7)P3=(Lα2-(2L+υ)α3+(L+υ)α4)P1+

(Lβ2-(2L+υ)β3+(L+υ)β4)P2+(-(2L+υ)γ3+(L+υ)γ4)P3,

得

2Kα3-(1+2K)α4=Lα2-(2L+υ)α3+(L+υ)α4,

即

Lα2-(2L+υ+2K)α3+(L+υ+2K+1)α4=0.

令ω=L+υ+2K+1,则有

Lα2-(ω+L-1)α3+ωα4=0.

2Kβ3-(1+2K)β4+α7=Lβ2-(2L+υ)β3+(L+υ)β4,

即

α7=Lβ2-(2L+υ+2K)β3+(L+υ+2K+1)β4，

α7=Lβ2-(ω+L-1)β3+ωβ4.

2Kγ3-(1+2K)2γ4+β7=-(2L+υ)γ3+(L+υ)γ4,

即

β7=-(2L+υ+2K)γ3+(L+υ+2K+1)γ4=-(ω+L-1)γ3+ωγ4=

-(ω+L-1)(1-α3-β3)+ω(1-α4-β4)=

(-(ω+L-1)+ω)+(ω+L-1)α3-ωα4+(ω+L-1)β3-ωβ4=

(1-L)+Lα2+(ω+L-1)β3-ωβ4=

(1-L)+L(1-β2)+(ω+L-1)β3-ωβ4=

1-Lβ2+(ω+L-1)β3-ωβ4=1-α7,

其中因υ是任意实常数,故ω也是任意实常数.

由上述分析可知下述定理成立：

定理3在(7),(9)式的变换条件下所生成的曲线段,若上述变换中的参数满足如下条件,则所生成的2条曲线段在连接点Q4=Q5处是G2连续的,且此二曲线C1与C2在拼接点处达到G2连续:

(ⅰ)(α5,β5,γ5)=(α4,β4,γ4);

(ⅱ)存在K>0,使得(α6,β6,γ6)=(1+K)(α4,β4,γ4)-K(α3,β3,γ3);

(ⅲ)存在L>0及实数ω,使得α7=Lβ2-(ω+L-1)β3+ωβ4，其中ω=L+υ+2K+1.

参考文献:

[1] 徐岗,汪国昭.带局部形状参数的三次均匀B样条曲线的扩展[J].计算机研究与发展,2007,44(6):1 032-1 037.

[2] 韩旭里,刘圣军.三次均匀B样条曲线的扩展[J].计算机辅助设计与图形学学报,2003,15(5):576-578.

[3] 王文涛,汪国昭.带形状参数的均匀B样条[J].计算机辅助设计与图形学学报,2004,16(6):783-788.

[4] 王文涛,汪国昭.带形状参数的三角多项式均匀B样条[J].计算机学报,2005,28(7):1 192-1 198.

[5] 王仁宏,李崇君,朱春刚.计算几何教程[M].北京：科学出版社,2008.

(责任编辑向阳洁)

Method of Shape Adjustment of Cubic B-Spline Curve

WANG Jingxin,JU Yan

(School of Mathematics,Liaoning Normal University,Dalian 116029,Liaoning China)

Abstract:This paper analyzes the structure of B-Spline Curve with local shape adjustment parameters,proposes the method of using transformation matrix with adjustment parameters to generate the control points,and then obtains the method of the objective Cubic B-Spline Curve with shape parameter.The study explores the influence of parameter change on the curve and the continuity conditions for generating Spline Curve at the splice point.

Key words:Cubic B-Spline Curve;adjustment parameters;matrix transformation

作者简介：王晶昕(1958—)，男，内蒙古赤峰人，辽宁师范大学数学学院教授，博士，主要从事计算数学研究.

基金项目：国家自然科学基金资助项目(11226326)

收稿日期：2014-09-21

中图分类号：O241.5

文献标志码：A

DOI:10.3969/j.issn.1007-2985.2015.02.006

文章编号：1007-2985(2015)02-0023-06