双α-链对角占优矩阵线性互补问题的误差界

彭　凌，莫宏敏

(吉首大学数学与统计学院，湖南 吉首 416000)



双α-链对角占优矩阵线性互补问题的误差界

彭凌，莫宏敏

(吉首大学数学与统计学院，湖南 吉首 416000)

摘要：根据双α-链对角占优矩阵的定义与性质，给出其线性互补问题的误差界.数值实例显示该误差界在判定线性互补问题近似解的精确性中是有效的.

关键词：精确性；误差界；线性互补问题；双α-链对角占优矩阵

双α-链对角占优矩阵在数学、物理、控制论以及经济学等许多领域有重要作用.双α-链对角占优矩阵也是非奇异H-矩阵，是一类范围很广的特殊矩阵，特别是关于双α-链对角占优矩阵的线性互补问题，也是数学规划中与凸二次规划密切相关的重要问题.近年来，国内外许多学者研究了多类特殊矩阵线性互补问题的误差界，取得了一些成果[1-3].笔者将根据双α-链对角占优矩阵的定义与性质，在文献[4]的基础上对其误差界进行改进，得到关于双α-链对角占优矩阵线性互补问题的新的误差界，并应用实例进行验证.

1预备知识

线性互补问题是指：存在一向量x∈Rn，使得

Mx+q≥0,x≥0,xT(Mx+q)=0，

其中M是n×n矩阵，q∈Rn.将线性互补问题记作LCP(M，q)，x*为LCP(M，q)的解.

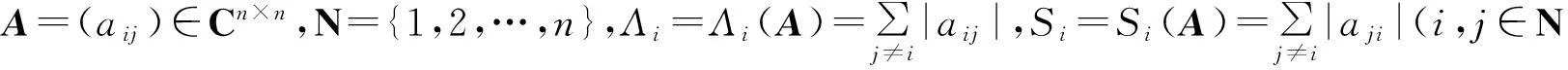
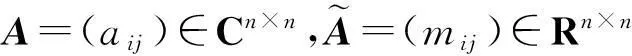
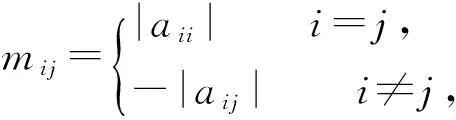
众所周知，具有正对角元的H-矩阵是一个P-矩阵.

定义2[5]若存在α∈[0,1]，使得∀i≠j(i,j∈N)，有

|aii||ajj|≥((Λi(A))α(Si(A))1-α)((Λj(A))α(Sj(A))1-α)

(1)

成立，则称A是双α-链对角占优矩阵.

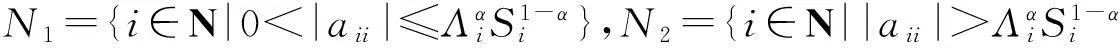
引理3若实矩阵A=(aij)∈Rn×n是双α-链对角占优矩阵，则存在正对角矩阵X=diag(x1,x2,…,xn)，AX是严格对角占优矩阵.其中：

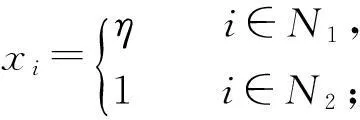
(2)

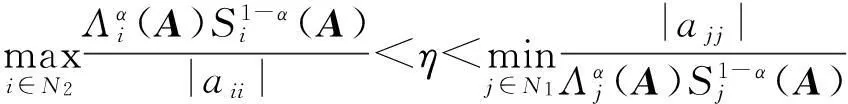
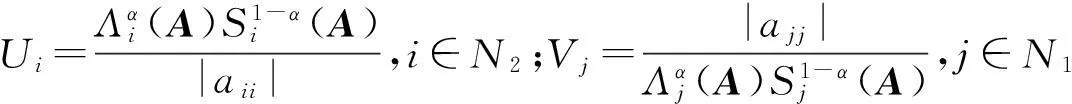
取正对角矩阵X=(x1,x2,…,xn)，当i∈N1时，xi=η，当j∈N2时，xj=1.令Q=AX=(qij)，易证qii-Λi(Q)>0,i∈N，所以AX是严格对角占优矩阵.

由引理1易知，若A=(aij)∈Rn×n是双α-链对角占优矩阵，则A是H-矩阵.

2主要结果及证明

考虑对角元素为正的双α-链对角占优矩阵M，易知M是P-矩阵.由文献[1]定理2.3的第3个不等式，对∀x∈Rn，有

其中：I是n×n单位矩阵；D是对角矩阵，D=diag(di),0≤di≤1,i=1,2,…,n；x*是LCP(M,q)的解；r(x)∶=min(x,Mx+q).由文献[1]定理2.1可知，当M=(aij)∈Cn×n是主对角元素为正的H-矩阵时，

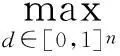
(3)

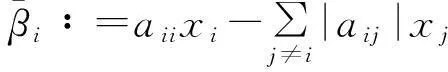
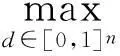
若η<1，则

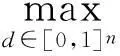
证明由引理1知，MX是主对角元素为正的严格对角占优矩阵.由文献[6]中定理A易证，对∀d∈[0,1]n，(I-D+DM)X也是主对角元素为正的严格对角占优矩阵，于是

‖(I-D+DM)-1‖∞=‖X(X-DX+DMX)-1‖∞≤‖X‖∞‖(X-DX+DMX)-1‖∞≤

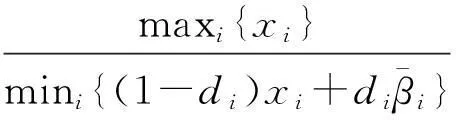
又因为

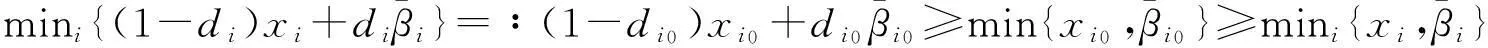
且i∈N2时，xi=1,当i∈N1时,xi=η，所以当η>1时，

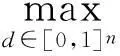
当η<1时，

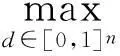
3数值实例

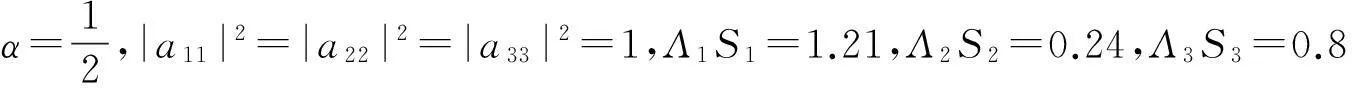
参考文献：

[1] BERMAN A,PLEMMONS R J.Nonnegative Matrices in the Mathematical Science[M].New York：Academic Press,1979.

[2] CHEN Xiaojun,XIANG Shuhuang.Computation of Error Bounds forP-Matrix Linear Complementarity Problems[J].Math. Program. Ser. A,2006，106:513-525.

[3] CVETKOVIC L,KOSTIC V,VARGA R S.A New Gersgorin-Type Eigenvalue Inclusion Set[J].Electron. Trans. Numer. Anal.,2004,18:73-80.

[5] 汪祥,卢琳璋.α-双对角占优与H矩阵的判定[J].厦门大学学报：自然科学版,2003,42(5):570-572.

[6] VARGA R S.On Diagonal Dominance Arguments for Bounding ‖A-1‖∞[J].Linear Algebra Appl.,1976,14:211-217.

(责任编辑向阳洁)

On Error Bound for Linear Complementarity Problem of Double

α-Chain Diagonally Dominant Matrix

PENG Ling，MO Hongmin

(College of Mathematics and Statistics，Jishou University,Jishou 416000，Hunan China)

Abstract:In this paper,we give new error bound for the linear complementarity problem where the involved matrix is a doubleα-chain diagonally dominant matrix based on its definition and properties.Preliminary numerical results show that the proposed error bound is efficient for verifying accuracy of approximate solutions.

Key words:accuracy;error bound;linear complementarity problem;doubleα-chain diagonally dominant matrix

作者简介：彭凌(1982—)，女，湖南怀化人，硕士研究生，主要从事矩阵理论与计算研究；莫宏敏(1969—)，男，湖南慈利人，吉首大学数学与统计学院副教授，博士，主要从事矩阵理论与计算研究.

基金项目：吉首大学校级科研项目(13JDY043)

收稿日期：2014-11-09

中图分类号：O151.21

文献标志码：A

DOI:10.3969/j.issn.1007-2985.2015.02.005

文章编号：1007-2985(2015)02-0020-03