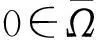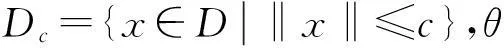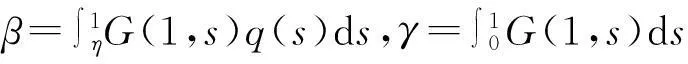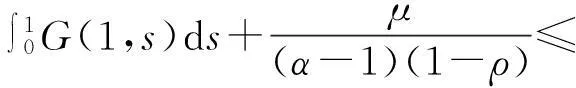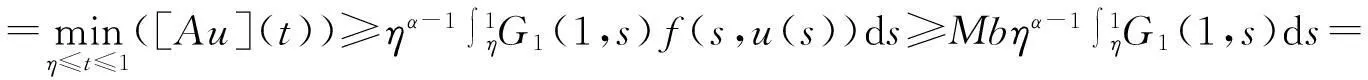一类含参数的分数阶微分方程边值问题
欧阳敏,钟文勇
(吉首大学数学与统计学院,湖南 吉首 416000)
一类含参数的分数阶微分方程边值问题

欧阳敏,钟文勇
(吉首大学数学与统计学院,湖南 吉首 416000)
摘要:利用不动点定理,研究一类含双参数的Riemann-Liouville 型分数阶微分方程多点边值问题正解的存在性及正解的重数,建立了边值问题至少存在1个或3个正解的充分条件.
关键词:分数阶微分方程;多点边值;正解;参数;不动点
近年来,分数阶微分方程已在数学、物理、生物、化学等学科及多孔介质、粘弹性材料等工程领域得到了重要应用[1],分数阶微分方程边值问题(简记为BVP)的理论研究得到学者们的高度关注并获得了很多研究成果.文献[2]研究了一类方程中含单个参数的Riemann-Liouville型分数阶微分方程三点BVP,文献[3]研究了一类边界条件含单个参数的Riemann-Liouville分数阶微分方程四点BVP.目前,含双参数的分数阶微分方程BVP还有待研究.笔者研究以下含双参数的高阶Riemann-Liouville 型分数阶微分方程多点BVP正解的存在性,得到了BVP正解的存在性和多解性的充分条件:
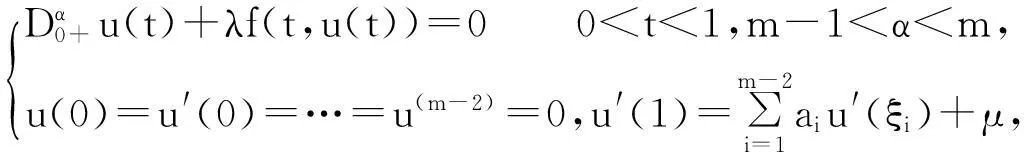
(1)
其中 λ及μ是正参数.
设 B=C[0,1] 表示区间[0,1]上连续函数按上确界范数构成的Banach空间,并作下列假设:
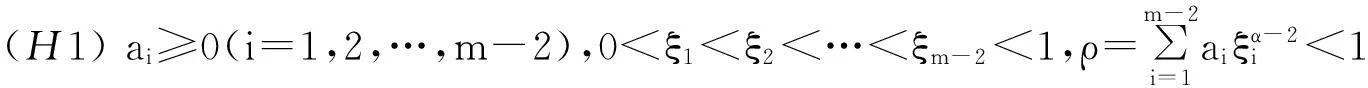
(H2) f:I×[0,∞)[0,∞)是连续函数.
1预备知识
定义1[1]函数y:(0,∞)R的α(α>0)阶分数阶积分定义为
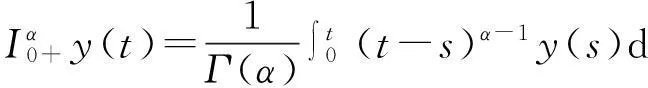
定义2[1]函数y:(0,∞)R的α(α>0)阶Riemann-Liouville型分数阶导数定义为
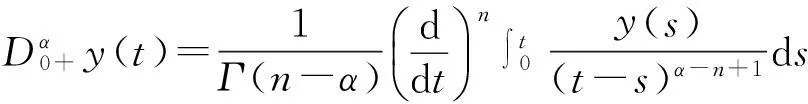
其中n=[α]+1,[α]表示α的整数部分.
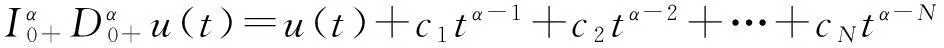
由引理1可得到如下结论:
引理2设g(t)∈C[0,1],若 (H1) 满足,那么BVP
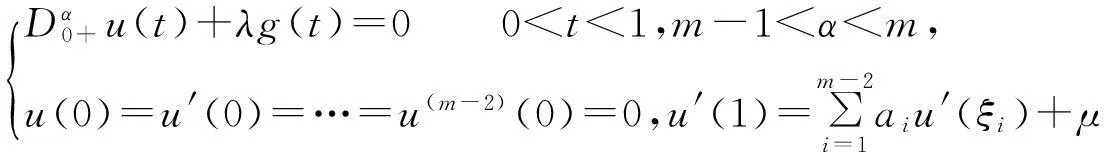
存在唯一解
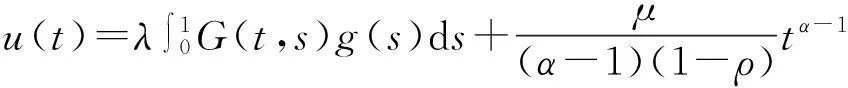
格林函数G定义为G(t,s)=G1(t,s)+G2(t,s),
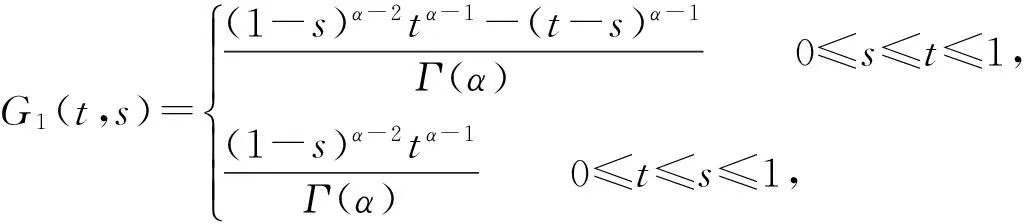
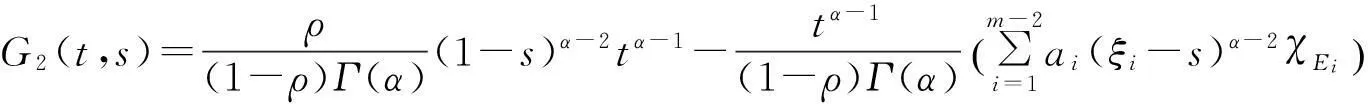
其中Ei=[0,ξi],χEi是集Ei(i=1,2,…,m-2)的特征函数.
引理3[4]设(H1)和(H4)成立,则对∀t,s∈[0,1]及i=1,2,有Gi(1,s)≥Gi(t,s)≥q(t)Gi(1,s)≥0,其中0 注1应用G(t,s)的定义及引理3容易得到G(1,s)≥G(t,s)≥q(t)G(1,s)≥0,t,s∈[0,1]. (ⅰ) ‖Ax‖≤‖x‖,x∈D∩∂Ω1及‖Ax‖≥‖x‖,x∈D∩∂Ω2; (ⅱ) ‖Ax‖≥‖x‖,x∈D∩∂Ω1及‖Ax‖≤‖x‖,x∈D∩∂Ω2. (ⅰ) {x∈(θ,b,d)|θ(x)>b}≠Ø对∀x∈(θ,b,d)有θ(Ax)>b; (ⅱ) 对∀x≤a,有‖Ax‖ (ⅲ) 若x∈P(θ,b,c)且‖Ax‖>d,则θ(Ax)>b. 其中‖x1‖ 注2若d=c,则由引理5条件(ⅰ)可以推出条件(ⅲ). 2主要结果及证明 定义锥D={u∈B|x(t)≥q(t)‖x‖,t∈[0,1]}.显然,对每一个u∈D有‖u‖=u(1).对给定的正数,定义Ωr={x∈B:‖x‖ 由引理 1、引理2及注1不难证明以下结论: 引理7若(H1),(H2)成立,则u∈C[0,1]是BVP(1)的解当且仅当它是算子A的不动点. 现定义几个常数: 并作如下约定:若f∞→∞,则1/βf∞=0;若F0→0,则1/γF0=∞;若f0→∞,则1/βf0=0;若F∞→0,则1/γF∞=∞. 定理1设条件(H1),(H2)成立.若βf∞>γF0,则对∀λ∈(1/βf∞,1/γF0)及充分小的μ,BVP(1)至少有1个正解. 故引理4条件(ⅰ)满足.即算子A至少有1个不动点,这不动点是BVP(1)的正解. 类似可证明如下结论: 定理2设条件(H1),(H2)成立.若βf0>γF∞,则对∀λ∈(1/βf0,1/γF∞)及充分小的μ,BVP(1) 至少有1个正解. 定理3设条件(H1),(H2)成立,且存在正常数a (ⅰ)f(t,x) (ⅱ)f(t,x)>Mb,(t,x)∈[η,1]×[b,c]; (ⅲ)f(t,x)≤Lc,(t,x)∈[0,1]×[0,c]. 其中 (1-δ)a≤δc+(1-δ)a≤c. 因此引理5条件(ⅰ)成立.由引理5和注2知算子A至少有3个不动点,由引理7可知这些不动点就是BVP(1)的正解. 参考文献: [1]KILBASAA,SRIVASTAVAHM,TRUJILLOJJ.TheoryandApplicationsofFractionalDifferentialEquations[M].Amsterdam:North-HollandMath.Stud.,ElsevierScienceB.V.,2006:204. [2]EL-SHAHEDM.PositiveSolutionsforBoundaryValueProblemofNonlinearFractionalDifferentialEquation[J/OL].Abstr.Appl.Anal.,2007,Vol. 2007,ArticleID10368:1-8[2014-09-20].http://www.hindawi.com/journals/aaa/2007/10368/. [3] 钟文勇.分数阶微分方程非齐次边值问题的正解[J].吉首大学学报:自然科学版,2010(3):10-14. [4]ZHONGWenyong.PositiveSolutionsforMultipointBoundaryValueProblemofFractionalDifferentialEquations[J/OL].Abstr.Appl.Anal.,2010,Vol. 2010,ArticleID601492:1-15[2014-09-20].http://www.hindawi.com/journals/aaa/2010/601492/. [5]KRASNOSEL’SKIIMA.PositiveSolutionsofOperatorEquations[M].Groningen:Noordhoff,1964. [6]LEGGETTR,WILIAMSL.MultiplePositiveFixedPointsofNonlinearOperatoronOrderedBanachSpaces[J].IndianaUniv.Math.,1979,28:673-688. (责任编辑向阳洁) Investigation on Multipoint Boundary Value Problems of Fractional Differential Equations with Parameters OUYANG Min,ZHONG Wenyong (College of Mathematics and Statistics,Jishou University,Jishou 416000,Hunan China) Abstract:This paper deals with the existence and multiplicity results of positive solutions to the multipoint boundary value problems of Riemann-Liouville fractional differential equations with two parameters.Using fixed-point theorems,some sufficient conditions are obtained to guarantee the existence of at least one or three solutions to the boundary value problems. Key words:fractional differential equations;multipoint boundary value;positive solutions;parameters;fixed points 作者简介:欧阳敏(1990—),女,湖南益阳人,吉首大学应用数学专业硕士研究生,主要从事微分方程研究;钟文勇(1963—),男,湖南吉首人,吉首大学数学与统计学院教授,博士,主要从事微分方程理论研究. 基金项目:湖南省自然科学基金资助项目(11JJ3007);吉首大学2014年校级科研项目(JDY048) 收稿日期:2014-12-31 中图分类号:O175.8 文献标志码:A DOI:10.3969/j.issn.1007-2985.2015.02.004 文章编号:1007-2985(2015)02-0016-04