随机凝聚算子的随机不动点定理及其应用

许绍元

(韩山师范学院数学与统计学系,广东 潮州 521041)



随机凝聚算子的随机不动点定理及其应用

许绍元

(韩山师范学院数学与统计学系,广东 潮州 521041)

摘要：利用随机凝聚算子的Leray-Schauder随机不动点定理,得到了随机凝聚算子的若干新的随机不动点定理,并将有关结果应用于随机积分方程.

关键词：随机全连续算子;随机凝聚算子;随机不动点;随机积分方程

1预备知识

随机不动点定理在研究各种随机微分方程和积分方程时起着十分重要的作用[1-6].文献[1]中引入随机拓扑度的概念，并将著名的Altman定理随机化，得到如下结果：

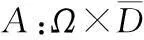
‖A(ω,x)-x‖2≥‖A(ω,x)‖2-‖x‖2∀(ω,x)∈Ω×∂D.

定理1是著名Altman定理的随机化推广.笔者旨在利用随机凝聚算子的Leray-Schauder随机不动点定理,得到随机凝聚算子的若干新的随机不动点定理,进而改进和推广了随机化的Altman定理，作为应用，得到积分核被二次函数控制后的一类随机积分方程的解.

2随机凝聚算子的随机不动点定理

首先，介绍一个有用的结论，即随机凝聚算子的Leray-Schauder不动点定理.

A(ω,x)≠μx∀(ω,x)∈Ω×∂D,μ≥1.

由引理1可以得到关于随机凝聚算子的一系列新的不动点定理.

‖A(ω,x)-x‖α·‖x‖β≥‖A(ω,x)‖α+β-‖x‖α+β∀(ω,x)∈Ω×∂D

(1)

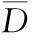
证明不妨设在∂D上没有不动点(否则定理结论成立).下证满足引理1的条件.事实上，若存在x0∈∂D，ω0∈Ω，μ0≥1使得A(ω0,x0)=μ0x0，则μ0>1.考虑函数f(t)=(t-1)α-tα+β+1,t>1.由于f(1)=0，f′(t)=α(t-1)α-1-(α+β)tα+β-1<0，∀t>1，因此f(t)在(1,+∞)上是严格单调减函数，故当t>1，f(t)1.由‖x0‖≠0，μ0>1,有

‖A(ω0,x0)-x0‖α·‖x0‖β=‖μ0x0-x0‖α·‖x0‖β=(μ0-1)α‖x0‖α+β<

这与条件(1)矛盾，故满足引理1的条件，从而在D上具有随机不动点ξ(ω)∈D.证毕.

由定理2立即得到随机凝聚算子的一系列随机不动点定理.

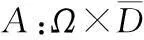
‖A(ω,x)-x‖α≥‖A(ω,x)‖α-‖x‖α∀(ω,x)∈Ω×∂D

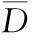
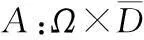
(ⅰ)‖A(ω,x)‖≤‖x‖,∀(ω,x)∈Ω×∂D;

(ⅱ)‖A(ω,x)‖≤‖A(ω,x)-x‖,∀(ω,x)∈Ω×∂D.

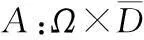
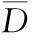
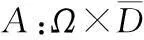
‖A(ω,x)-x‖·‖x‖≥‖A(ω,x)‖2-‖x‖2∀(ω,x)∈Ω×∂D,

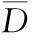
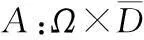
‖A(ω,x)-x‖·‖x‖≥‖A(ω,x)‖2∀(ω,x)∈Ω×∂D,

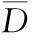
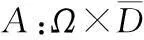
‖A(ω,x)-x‖·‖x‖α-1≥‖A(ω,x)‖α-‖x‖α∀(ω,x)∈Ω×∂D，

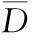
‖A(ω,x)+x‖α+β≤‖A(ω,x)‖α‖x‖β+‖x‖α+β∀(ω,x)∈Ω×∂D

(2)

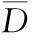
证明不妨设在∂D上没有不动点(否则定理结论成立).下证满足引理1的条件.事实上，若存在x0∈∂D，ω0∈Ω，μ0≥1使得A(ω0,x0)=μ0x0，则μ0>1.考虑函数f(t)=(t+1)α+β-tα-1,t>1.由于f(1)=0，f′(t)=(α+β)(t+1)α+β-1-αtα-1>0，∀t>1，因此f(t)在(1,+∞)上是严格单调增函数，故当t>1，f(t)>f(1)=0，即tα-1<(t+1)α+β,∀t>1.由‖x0‖≠0，μ0>1,有

‖A(ω0,x0)+x0‖α+β=‖μ0x0+x0‖α+β=(μ0+1)α+β‖x0‖α+β>(μα+1)0‖x0‖α+β=

‖A(ω0,x0)‖α‖x0‖β+‖x0‖α+β.

这与条件(2)矛盾，故满足引理1的条件，从而在D上具有随机不动点ξ(ω)∈D.证毕.

由定理3立即得到随机凝聚算子的一系列随机不动点定理.

‖A(ω,x)+x‖α≤‖A(ω,x)‖α+‖x‖α∀(ω,x)∈Ω×∂D

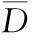
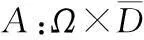
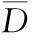
注1由于随机全连续算子必定是随机凝聚算子，因此定理2、定理3及其推论对A(ω,x)是随机全连续算子时结论仍然成立.

注2定理2推广了文献[6]中定理2和定理3，定理9推广了文献[6]中定理5.

3应用举例

例1考察随机yPbICOH积分方程：

φ(x)=∫Gk(ω,x,y,φ(y))dy，

(3)

其中G是Rn中有界开集,Ω为完全概率测度空间.

设k(ω,x,y,u)在(ω,x,y)∈Ω×G×G,-∞<μ<+∞上随机连续,且满足不等式

|k(ω,x,y,u)|≤a+b|u|+cu2∀(ω,x,y)∈Ω×G×G,-∞<μ<+∞，

证明利用文献[5]中定理2.1的证明方法可知积分算子A(ω,φ)=∫Gk(ω,x,y,φ(y))dy是映Ω×C(G)→C(G)的随机全连续算子,它必然是随机凝聚算子.当c=0时，令

当c>0时，令

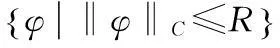
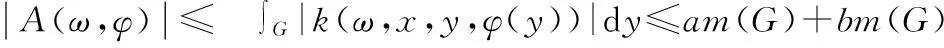
m(G)(a+bR+cR2)=R，

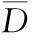
注3与文献[6]的例子不同的是，本例对随机yPbICOH积分方程(3)给出了新的定解条件，从而解决了方程(3)的核被u的二次函数控制后方程的解的存在性问题，而文献[6]只讨论了被u的一次函数控制的特殊情况.因此，本例不仅推广和包含了文献[6]的有关结论，而且是文献[6]的一个有益补充.

参考文献：

[1]LIGuozhen，CHENYuching.OnRandomTopologicalDegreeandSomeRandomFixedPointTheorems[J].ActaMathematicaScientia，1993,13(4)：391-398.

[2]BHARUCHA-REIDAT.RandomIntegralEquations[M].NewYork：AcademicPress,INC,1972.

[3] 朱传喜.关于随机算子方程的随机解[J].数学进展,1997,26(5)：429-434.

[4]LIGuozhen.TheExistenceTheoremsoftheRandomSolutionsforRandomHammerstainEquationswithRandomKernel(Ⅱ)[J].AppliedMathematicsLetters,2002,15(1):121-125.

[5]LIGuozhen，DEBNATHL.TheExistenceTheoremsoftheRandomSolutionsforRandomTypeNonlinearIntegralEquations[J].AppliedMathematicsLetters,2000,13:111-115.

[6] 李国祯,许绍元.关于随机非线性算子的若干定理[J].数学进展,2006,35(6):721-729.

(责任编辑向阳洁)

On Random Fixed Point Theorems of Random Condensing

Operators and Applications

XU Shaoyuan

(Department of Mathematics and Statistics,Hanshan Normal University,Chaozhou 5210410，Guangdong China)

Abstract:In this paper,by using the so-called Leray-Schauder random fixed point theorem,we obtain a number of new random fixed point theorems.The corresponding result is applied to a class of random nonlinear integral equations.

Key words:random completely continuous operators;random condensing operators;random fixed points;random integral equations

作者简介：许绍元(1964—)，男，湖北武汉人，韩山师范学院数学与统计学系教授，博士后，主要从事非线性泛函分析与分形几何研究.

基金项目：韩山师范学院2013年“创新强校工程”创新强系科研项目

收稿日期：2014-08-29

中图分类号：O177.91

文献标志码：A

DOI:10.3969/j.issn.1007-2985.2015.02.002

文章编号：1007-2985(2015)02-0008-03