Sugeno测度空间上局部风险最小化估计的界

白云超,冯贺平，白鹤举

(1.河北大学 经济学院，河北 保定　071002；2.河北软件职业技术学院 智能工程系，河北 保定　071000;

3.承德石油高等专科学校 基础教学部，河北 承德　067000)



Sugeno测度空间上局部风险最小化估计的界

白云超1,冯贺平2，白鹤举3

(1.河北大学 经济学院，河北 保定071002；2.河北软件职业技术学院 智能工程系，河北 保定071000;

3.承德石油高等专科学校 基础教学部，河北 承德067000)

摘要：在Sugeno测度空间上，为了将结构风险最小化原则应用于局部函数估计问题，给出了局部风险最小化估计问题的思想，并证明了局部风险最小化估计的界.

关键词：局部风险最小化估计；邻域函数；gλ测度空间；结构风险最小化

MSC 2010：90C70

第一作者： 白云超(1977-)，女，河北承德人，河北大学副教授，主要从事不确定性统计学习理论研究.

E-mail:yunchaobai@126.com

在非可加测度空间[1-2]上,统计学习理论的关键定理，经验风险最小化原则和学习过程一致收敛速度的界和结构风险最小化原则[3-8]已经给出.无论经验风险最小化原则还是结构风险最小化原则，对于从有限数量的观测估计函数中最小化风险泛函，必须明确研究问题的信息，比如在模式识别和支持向量机[9-10]中的结构风险最小化原则问题中，都需要找到一个结构，该结构1/h较小的时候可以提供较小的经验风险泛函的值.然而，为了找到该结构必须获得关于所研究问题的信息，但是事实上并不能获取所研究问题的全部信息.为了避免从所有结构中选择差结构，考虑新的思路：函数的局部估计，即在感兴趣的点附近进行函数估计.通过局部地逼近函数，就可以达到较好的逼近精度，如何从所有的结构中找到好的结构，文章从具有代表性的非概率测度—gλ测度上，给出了局部风险最小化估计的思想，并证明了局部风险最小化估计的界.

1预备知识

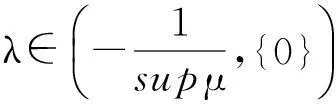
μ(E∪F)=μ(E)+μ(F)+λμ(E)μ(F)，

其中E∈ζ,F∈ζ,E∪F∈ζ,E∩F∈Φ.

称μ满足有限λ-律当且仅当存在上述λ使得下式成立,

其中{E1,E2,…,En}是ζ中有限不交类，且它们的并集也在ζ.

定义2[1]设F是p(X)上的σ-algebra.μ称为F上的Sugeno测度，当且仅当μ满足σ-λ律并且μ(X)=1.简记为gλ.

命题1[1]如果μ是F上的Sugeno测度，则μ是单调的.

命题2[1]如果μ是F上的Sugeno测度，则μ(Φ)=0且满足有限λ-律.

命题3[1]对于任意一个Sugeno测度gλ，总可以找到一个T-函数，使得集函数θλ∘gλ为一个概率测度P，且此T-函数为

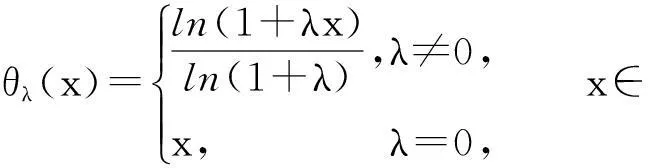
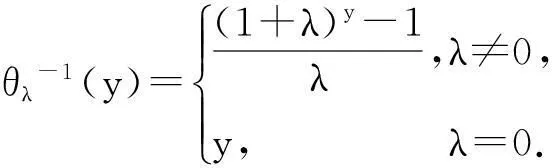
命题4[7]Sugeno测度gλ是双零渐进可加的，如果∀{An}⊂F,{Bm}⊂F,并且当gλ(An)→0,gλ(Bm)→0时，则μ(An∪Bm)→0(n→∞,m→∞).

2Sugeno测度空间上局部风险最小化估计的界

设(x1,y1),(x1,y2),…,(xl,yl)是已知的独立同分布的样本数据，Fgλ(x,y)是未知sugeno测度，K(x,x0,β)是一个非负的邻域函数，与x0和β∈(0,∞)有关，并满足以下2个条件：

(1)

目标是在函数集f(x,α),α∈Λ和点x0的不同邻域函数上最小化局部风险泛函

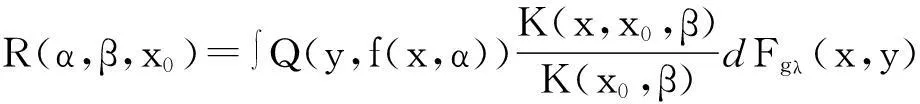
(2)

然后利用结构风险最小化原则来最小化基于经验数据的局部风险泛函.为此提出有关局部风险泛函界的估计定理.

定理1设指示函数集Q(y,f(x,α)),α∈Λ的VC维是h1，非负实函数集K(x,x0,β),β∈(0,∞)的VC维是h2，则对于所有α∈Λ和所有β∈(0,∞)，不等式

成立，其中局部经验风险泛函为

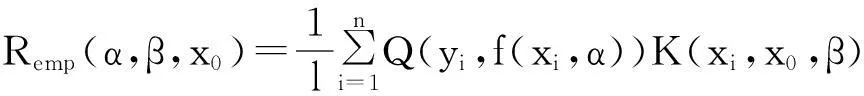
(3)

局部期望风险泛函为

R*(α,β,x0)=∫Q(y,f(x,α))K(x,x0,β)dFgλ(x,y)，

(4)

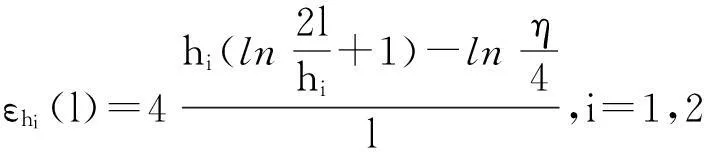
(5)

邻域函数的经验风险函数为

(6)

证明：因为Q(y,f(x,α))×K(x,x0,β)是完全有界的，并且界是1；在Sugeno测度空间上推导出来风险的界[7]，对所有的函数集和所有的邻域参数值都是成立的.根据文献[7]中的定理7，对于所有的α∈Λ和β∈(0,∞)，不等式

成立，其中εhi(l)由式(5)给定.

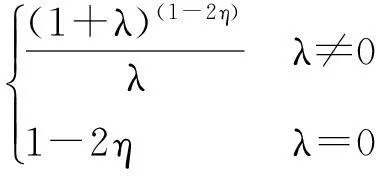
(7)

根据式(1)和K(x,x0,β),β∈(0,∞)的VC维是h2，得到

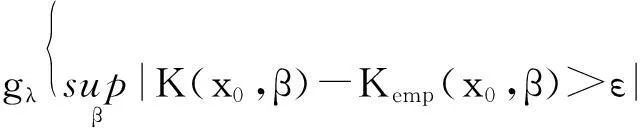
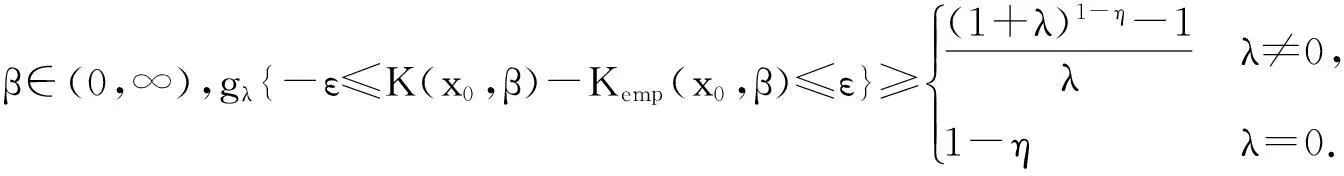
那么

(8)

根据式(7)和(8)，得到

下面给出无界损失函数Q(y,f(x,α)),α∈Λ的情形，考虑局部函数的界.根据Sugeno测度空间上无界非负函数集的界，考虑一个更强的约束条件.

假定不等式

(9)

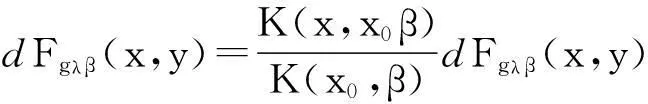
(10)

定义了与参数有关的一个Sugeno测度族.

定理2设非负函数集θ(Q(y,f(x,α)))×K(x,x0,β),α∈Λ,β∈(0,∞)具有VC维是h*且满足不等式(9), 又设邻域函数K(x,x0β),β∈(0,∞)的VC维是h2，则对于所有的α∈Λ和β∈(0,∞)，不等式

证明：为了证明定理，根据文献[7]中定理4，下列不等式成立

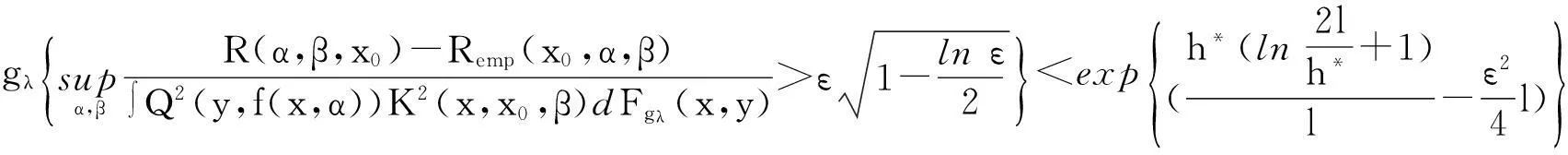
(11)

由于0≤K(x,x0,β)≤1和不等式(10) 成立，所以

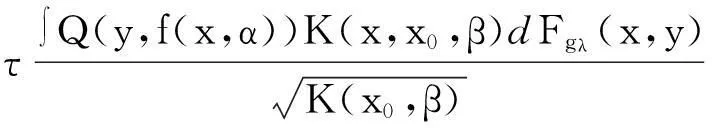
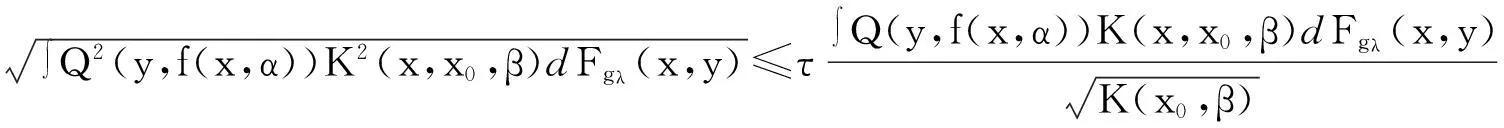
(12)

利用不等式(11)和(12)，得

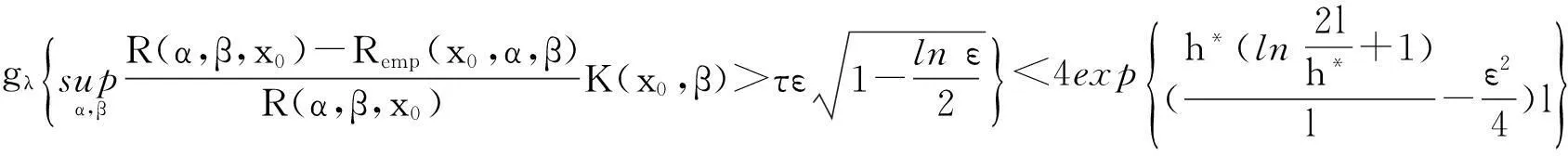
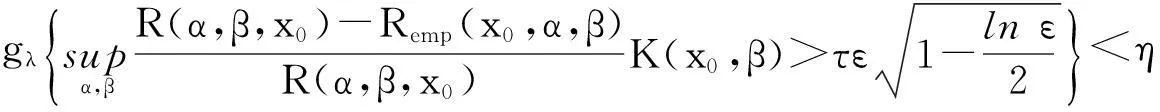
因此对于任意α∈Λ和β∈(0,∞)，不等式

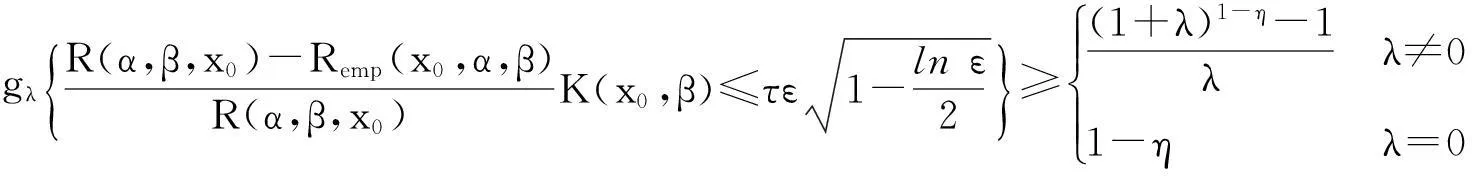
(13)

3局部函数估计的结构风险最小化原则

利用定理1和定理2所提供的界，可以将结构风险最小化原则应用于局部函数估计问题.无论是模式识别还是回归估计问题，结构风险最小化的方法是一样的，都是考虑含嵌套元素sk的结构，在每个元素sk上选取最好的函数Q(y,f(x,α)),α∈Λ和最好的邻域函数K(x,x0,β),β∈(0,∞)，然后只需要最小化定理1、定理2的右端，就能够估计出损失函数的界.

参考文献:

[1]WANG Zhenyuan, GEORGE J Klir. Fuzzy measure theory [M]. New York ：Plenum Press , 1992.

[2]哈明虎，王超，张植明，等．不确定统计学习理论[M]．北京：科学出版社,2010.

[3]哈明虎，冯志芳，宋士吉，等．拟概率空间上学习理论的关键定理和学习过程一致收敛速度的界[J]．计算机学报,2008,31(3)：476-485．

HA Minghu, FENG Zhifang, SONG Shiji,et al. The key theorem and the bounds on the rate of uniform convergence of statistical learning theory on quasi-probability spaces[J]. Chinese Journal of Computers, 2008,31(3)：476-485．

[4]李俊华，李海军.受噪声影响的复hybrid样本的学习理论关键定理[J]. 河北大学学报：自然科学版,2014,34(1):14-18.

LI Junhua, LI Haijun.Key theorem of learning theory with complex hybrid samples corrupted by noise[J]. Journal of Hebei University：Natural Science Edition, 2014, 34(1): 14-18.

[5]HA Minghu,BAI Yunchao,WANG Peng,et al, The key theorem and the bounds on the rate of uniform convergence of learning theory on credibility meassure spaces[J]. Advances in Fuzzy Sets and Systems,2006,1(2):143-172.

[6]周彩丽，哈明虎，鲍俊艳，等．基于模糊数的模糊学习理论的关键定理[J]．河北大学学报：自然科学版，2008,28(5):449-451．

ZHOU Caili, HA Minghu, BAO Junyan, et al. Key theorem of learning theory based on fuzzy number[J].Journal of Hebei University：Natural Science Edition,2008,28(5):449-451.

[7]哈明虎，李颜，李嘉，等．Sugeno测度空间上学习理论的关键定理和一致收敛速度的界[J]．中国科学：E辑信息科学，2006,36(4):398-410．

HA Minghu, LI Yan, LI Jia, et al.The key theorem and the bounds on the rate of uniform convergence of learning theory on sugeno measure spaces[J].Science in China：Series E, Information Science,2006,36(4):398-410.

[8]BAI Yunchao. Structures risk minization principle on Sugeno space [J]. ICMLC, 2008, 7(2): 829-834.

[9]张学工.关于统计学习理论和支持向量机[J].自动化学报，2000,26(1):32-42.

[10]张植明,田景峰.Sugeno测度空间基于复样本的统计学习理论[J].计算机工程与应用，2009,45(7):59-64.

ZHANG Zhiming, TIAN Jingfeng. Statistical learning theory complex samples on Sugeno measure space[J].Computer Engineering and Applications, 2009,45(7):59-64.

(责任编辑：王兰英)

Bound of local risk minimization estimation on Sugeno measure space

BAI Yunchao1,FENG Heping2,BAI Heju3

(1.College of Economics Science, Hebei University, Baoding 071002,China;

2.Intelligent Engineering Department,Hebei Software Institute,Baoding 071000,China;

3.Basic Teaching Department,Chengde Petroleum College, Chengde 067000,China)

Abstract:On Sugeno measure space, the ideas of local risk minimization estimation problem is presented.In order to make the principle of structural risk minimization apply to the problem of local risk minimization estimation, the paper gives and proves the bounds of the bound of local risk minimization estimation.

Key words:local risk minimization estimation; vicinity function;gλmeasure space； structural risk minimization

基金项目：河北省软科学项目(13456123)

收稿日期：2015-03-17

中图分类号：TP18;O159

文献标志码:A

文章编号：1000-1565(2015)06-0566-05

DOI：10.3969/j.issn.1000-1565.2015.06.002