带周期边界条件时间分数阶扩散方程逆时反问题的条件稳定性

阮周生，张文，王泽文

(1.东华理工大学 放射性地质与勘探技术国防重点学科实验室，江西 南昌　330013；

2.东华理工大学 理学院，江西 南昌　330013)



带周期边界条件时间分数阶扩散方程逆时反问题的条件稳定性

阮周生1，2，张文1，2，王泽文2

(1.东华理工大学 放射性地质与勘探技术国防重点学科实验室，江西 南昌330013；

2.东华理工大学 理学院，江西 南昌330013)

摘要：基于伴随思想，利用分离变量方法研究了一类带周期边界条件时间分数阶扩散方程，首先在弱解意义下推得了正问题解的正则性，然后基于对初值的光滑性假设推得了逆时反问题条件稳定性结论.

关键词：时间分数阶扩散方程; 逆时反问题；条件稳定性

MSC 2010：35K05

第一作者：阮周生(1980)，江西吉安人，东华理工大学讲师，博士，主要从事偏微分方程正反问题理论与数值方法研究.

E-mail:zhshruan@126.com

本文考虑初边界问题

(1)

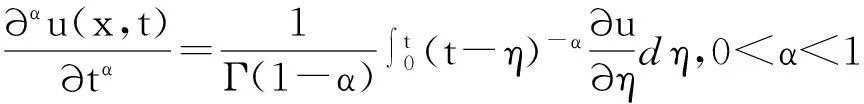
(2)

Γ(1-α)为伽马函数.

上面定解问题中边界条件含有周期边界条件，是非局部的.对带有非局部边界条件定解问题的数值研究始于文献[1]. 带非局部边界的定解问题具有特殊的性质，因为对应的空间微分算子不是自伴算子，故对应的特征函数系统不是完备的系统，需要通过伴随函数来对特征函数系统完备化.

Ionkin等[2]利用分离变量法证明了二维带非局部边界条件热传导方程定解问题解的存在性、唯一性及解对初值的稳定性.Sergei[3]考虑了一类带积分非局部边界条件的初边值波动方程问题，通过对定解条件的合理假设，利用Fourier分析方法证明了该问题经典解的存在性与唯一性. 整数阶带非局部边界条件定解问题数值方法研究可以参考文献[4-7].Benchohra等[8]研究了Caputo分数阶微分方程带非局部边界条件定解问题解的存在性条件.文献[9-11]分别利用拟逆法、优化方法和数据正则化方法研究带Dirichlet边界条件的时间分数阶扩散方程逆时反问题，带非局部边界条件分数阶微分方程反问题的研究可参考文献[12-13].

上面所述带非局部边界条件分数阶微分方程正问题的研究是基于经典解意义下考虑的，带非局部边界条件逆时问题的研究仅仅局限于反问题解的存在性、唯一性研究，针对逆时反问题条件稳定性问题不曾考虑. 本文对以上的研究结果做进一步研究，首先在弱解的意义下研究解的正则性，而后推导出逆时反问题的条件稳定结果.

1弱解及基本引理

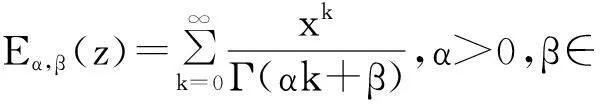
引理1[12-13]Mittag-Leffler函数满足

给出弱解定义.

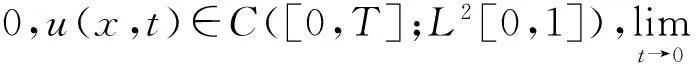
已知特征系统

X″(x)+λX=0,x∈(0,1),X(0)=0,X′(0)=X′(1).

(3)

对应的特征值和特征函数系为

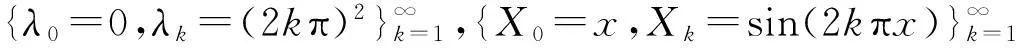
(4)

(5)

可推得伴随问题对应的特征函数系统为

(6)

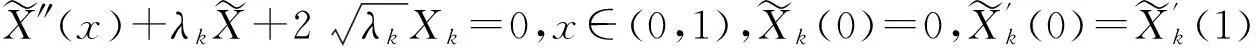
(7)

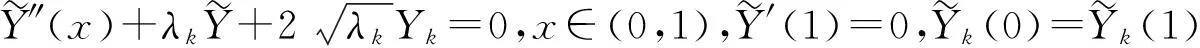
(8)

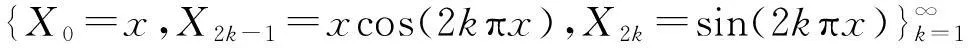
(9)

同理，对伴随特征系统重排可得

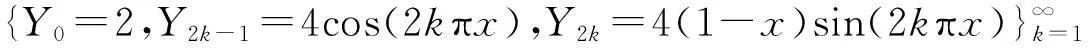
(10)

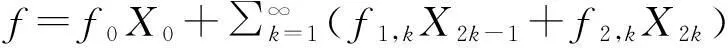
f0=(f,Y0),f1,k=(f,Y2k-1),f2,k=(f,Y2k),k=1,2,….

(11)

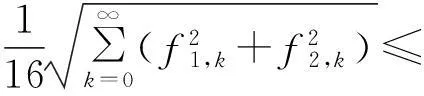
为了证明方便， 给出辅助函数Hk(t)定义并证明其相关性质.

定义3

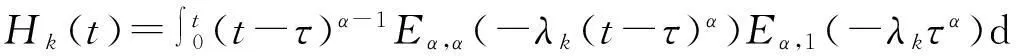
(12)

引理3

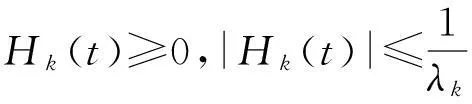
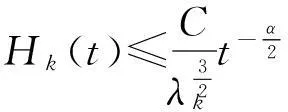
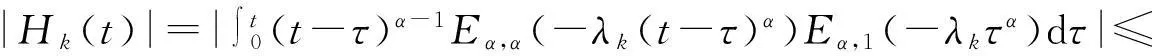
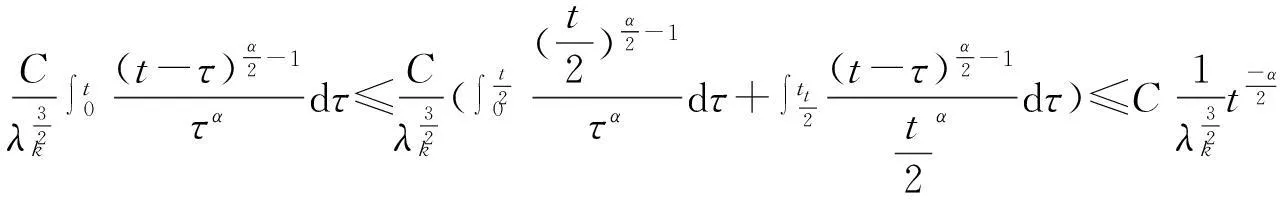
2正问题解的正则性及逆时反问题条件稳定性

利用分离变量法求问题(1)的级数形式解，设问题(1)的形式解为

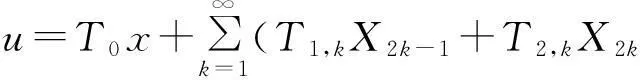
(13)

将式(13)代入问题(1)得

(14)

(15)

为了后续表示方便，形式上记解算子K:φ→u(.,T)， 故有

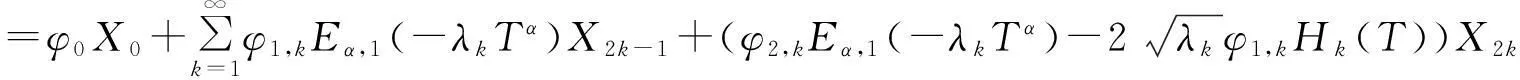
(16)

给出问题(1)解的正则性结论.

定理1当φ(x)∈L2[0,1],可推得问题(1)存在唯一的弱解u(x,t)，使得u∈C([0,T];L2[0,1])∩C((0,T];H2[0,1]),且存在常数C,满足

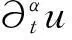
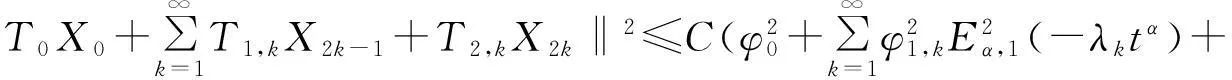
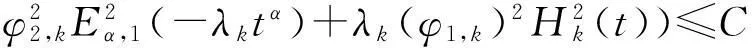
形式推导有

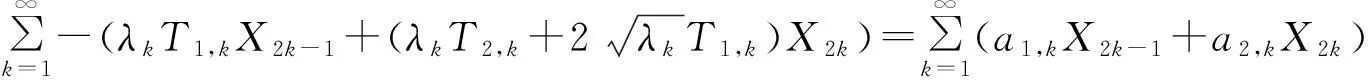
其中

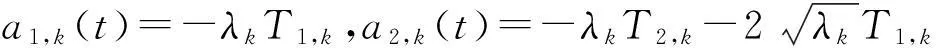
经计算得

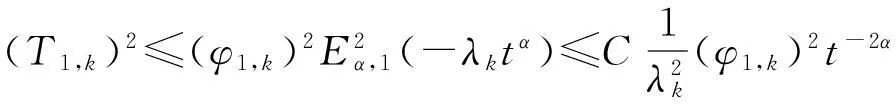
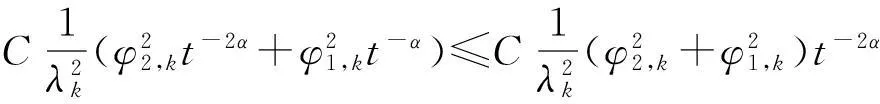
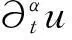
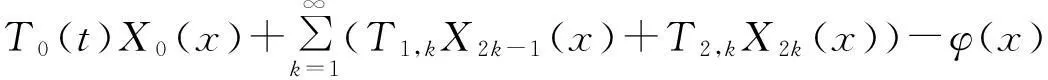
由Lebesgue控制收敛定理，

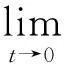
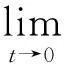
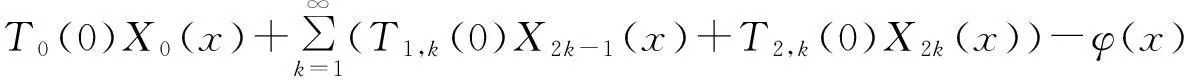
接下来证明弱解的唯一性，由弱解定义，只需要证明当φ(x)=0时，问题只有平凡解.

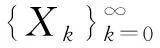
由分数阶常微分方程解的存在唯一性结论[15]得Ti,k(t)=0,i=1,2,k=1,2,…,故u(x,t)≡0,(x,t)∈[0,1]×[0,T]，综合可知，定理得证.

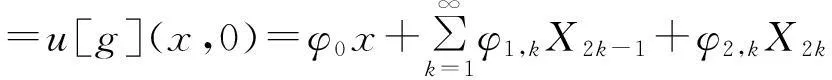
(17)

当φ(x)∈H2[0,1]，可以推得

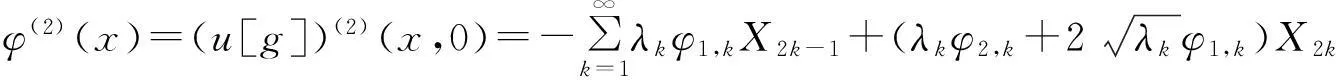
(18)

定理2(条件稳定性)若φ(x)∈H2[0,1],且‖φ(x)‖H2[0,1]≤U0，则有下面条件稳定性结果

(19)

证明：

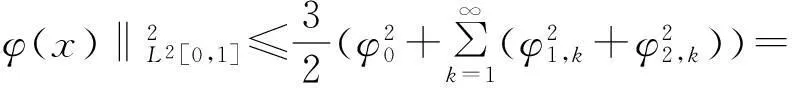
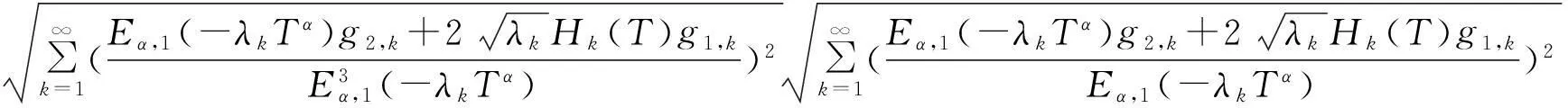
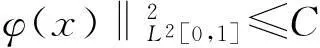
3小结

本文基于分离变量法考虑了一类带周期边界条件的时间分数阶扩散方程正反问题，通过对初始条件的先验假设，推得了初值反问题的条件稳定性结论，从结论中看出带周期边界条件的时间分数阶逆时反问题是中度不适定的，比整数阶逆时反问题不适定性要稍弱.

参考文献:

[1]BITSADZEAV,SAMARSKIIAA.Someelementarygeneralizationsoflinearellipticboundaryvalueproblems[J].DokLAkadNaukSSSR,1969,185(4): 739-740.

[2]IONKINNI,MOROZOVAVA.Thetwo-dimensionalheatequationwithnonlocalboundaryconditions[J].DifferEq,2000,36(7): 982-987.

[3]BEILINSA.Existenceofsolutionsforone-dimensionalwaveequationswithnonlocalconditions[J].ElectronJDifferEq,2001,76:1-8.

[4]BOUZIANIA.Onaclassofparabolicequationswithanonlocalboundarycondition[J].AcadRoyBelgBullClSci,1999,10: 61-77.

[5]BOUZIANIA,MERAZGAN,BENAMIRAS.Galerkinmethodappliedtoaparabolicevolutionproblemwithnonlocalboundaryconditions[J].NonlinearAnal,2008,69: 1515-1524.

[6]LINYanping,XUShuzhan,YINHongming.Finitedifferenceapproximationforaclassofnonlocalparabolicequations[J].IntJMathMathSci,1997,20:147-164.

[7]WANGShingmin,LINYanping.Anumericalmethodforthediffusionequationwithnonlocalboundaryspecifications[J].IntJEngrgSci,1990,28(6): 543-546.

[8]BENCHOHRA M,HAMANI S,NTOUYAS S K. Boundary value problems for differential equations with fractional order and nonlocal conditions[J]. Nonlinear Anal-Theor,2009,71(7): 2391-2396.

[9]LIU Jijun, YAMAMOTO M. A backward problem for the time-fractional diffusion equation[J]. Appl Anal,2010,89(11): 1769-1788.

[10]XIONG Xiangtuan, LI Ming. An optimal method for fractional heat conduction problem backward in time[J]. Appl Anal,2012,91(4): 823-840.

[11]WANG Liyan, LIU Jijun. Data regularization for a backward time-fractional diffusion problem[J]. Comput Math Appl,2012,64: 3613-3626.

[12]KIRANE M,MALIK S A,GWAIZ M A. An inverse source problem for a two dimensional time fractional diffusion equation with nonlocal boundary conditions[J]. Math Meth Appl Sci， 2013,36:1056-1069.

[13]KIRANE M,MALIK S A. Determination of an unknown source term and the temperature distribution for the linear heat equation involving fractional derivative in time[J]. Appl Math Comput,2011,218:163-170.

[14]KELDYSH M V.On eigenvalues and eigenfunctions of certain classes of not self-adjoint equations[J]. Doklady Acad Nauk SSSR,1951,87:11-14.

[15]PODLUBNY I. Fractional differential equations:an introduction to fractional derivatives，fractional differential equations,to methods of their solution and some of their applications[M]. San Diego: Academic Press,1999.

(责任编辑：王兰英)

Conditional stability of backward problem for a time fractional

diffusion equation with periodic boundary condition

RUAN Zhousheng1，2，ZHANG Wen1，2，WANG Zewen2

(1. Key Laboratory for Radioactive Geology and Exploration Technology, Fundamental Science for

National Defense，East China University of Technology，Nanchang 330013，China;

2.College of Science， East China University of Technology， Nanchang 330013，China)

Abstract:Based on the adjoint idea， a kind of time fractional diffusion equation with periodic boundary condition by method of separation of variables was considered. Firstly， the regularization result of the solution to the direct problem in the sense of weak solution was derived. Then based on the smoothing assumption for the initial data， the conditional stability for the backward problem was gived.

Key words:time fractional diffusion equation; backward problem; conditional stability

基金项目：国家高新技术研究发展计划(2012AA061504)；国家自然科学基金资助项目(11561003)；放射性地质与勘探技术国防重点学科实验室资助项目(RGET1513)；江西省高校科技落地计划资助项目(KJLD14051)

收稿日期：2015-01-10

中图分类号：O175

文献标志码:A

文章编号：1000-1565(2015)06-0561-05

DOI：10.3969/j.issn.1000-1565.2015.06.001