简论二维记法的概念文字
夏素敏
(中国社会科学院 哲学研究所,北京 100732)
简论二维记法的概念文字
夏素敏
(中国社会科学院 哲学研究所,北京100732)
摘要:图形及其逻辑的研究正在吸引越来越多的注意,而现代逻辑自诞生起就以一种二维记法——弗雷格的概念文字出现。同时代的皮尔士也以二维方式建立了一套逻辑图形系统——存在图。为了探讨弗雷格的概念文字和皮尔士的存在图之间的联系,在阐述弗雷格的概念文字的相关内容的基础上,根据已有的研究进展,利用《形式的规律》以及皮尔士存在图的一些思想把弗雷格逻辑图形看成是一种信息处理网络,由此我们可以看到弗雷格蕴涵图与皮尔士推演指号及其内部结构之间的类似之处。
关键词:弗雷格逻辑图;《形式的规律》;皮尔士存在图
中图分类号:B81
文献标识码:A
文章编号:1674-8425(2015)12-0021-04
Abstract:The study of graphics and its logic is attracting more and more attention, and the modern logic is born with a two-dimensional concept notation of Frege. In the same time, Peirce has set up a set of logical diagrams system-existence figure in the same way. In order to explore the relationship between the concept notation of Frege and Peirce’s existential graphs, the paper described the concept of Frege’s concept notation of the text, and based on the existing research progress, we treated the use of Laws of Form and the existential diagramsof some ideas of Frege’s logical diagrams as a kind of information processing network, which we can see the similarities between implication diagrams of Frege and the deduction signals of Peirce.
收稿日期:2015-07-26
基金项目:国家社会科学基金青年项目“实验哲学的批判性研究”(14CZX015)
作者简介:赵亮英(1981—),女,江西分宜人,讲师,哲学博士,研究方向:分析哲学、科学哲学。
doi:10.3969/j.issn.1674-8425(s).2015.12.006
Brief Discussion On Concept Notation of Two-Dimension Notation
XIA Su-min
(Institute of Philosophy, Chinese Academy of Social Sciences, Beijing 100732, China)
Key words: Frege’s logical diagram;LawsofForm;Peirce’s existential graph
1879年,弗雷格在其《概念文字》中给出逻辑的二维符号系统,于是现代逻辑以一种图形的面貌出现。这些逻辑图形被弗雷格认为超越了自然语言和其他构造出来的语言的特殊局限性。但是,逻辑学后来的发展并没有接受弗雷格的这些图形,因为这个符号系统的“不幸之处在于其累赘不堪而实际使用起来极其困难”[1]24。有意思的是,弗雷格设计这套图形的目的恰恰就是为了帮助我们的推理实践:“它的主要目的在于以最可靠的方式检验推理系列。”[2]87与弗雷格大约同时期的另一位现代逻辑创始人皮尔士建立的一套逻辑图形——存在图,同样也被长期忽视。根据已有的相关研究,笔者在英国数学家斯宾塞·布朗的《形式的规律》[3]基础上致力于考察这两种逻辑图形的联系和在当前的意义。
一、弗雷格的“概念文字”
弗雷格的概念文字记法可以表达“一个正确推论所必要的所有东西”[4]8,并且这种表达要求“逻辑关系通过书写记号清楚地表示出来”[5]14,这些书写记号正是“逻辑关系的符号”[2]89。他认为,“一个简单的序列排序绝不能对应思想中相互关联的逻辑关系的多样性”,他设计的二维记法是“有助于理解我们想要的、能引起我们兴趣的东西”[2]87。
在逻辑图中,弗雷格的条件竖是弗雷格为初始逻辑关系创设的指号,正是这一条件竖记号为他的逻辑语言提供了二维特征。由此,我们需要从一种揭示其逻辑理由的方式来理解这一记号。在标准读法中,弗雷格逻辑的条件竖所起的作用与现在的马蹄号(即实质蕴涵符号)作用是一样的。
我们知道,图1中的概念文字条件句只在或者B为假或者A为真的情况下指示真。由此,它表达的是由B⊃A表达的思想。图2则否定了下述情形:在这种情形中,A被否定而B和Γ都被肯定。Γ和图1结合起来的构造方式与图1内部B与A的构造方式是一样的。这样理解的话,那么图1就是相对于条件Γ的一个整体单位。由此,前者就具有了“如果Γ,那么,若B则A”的形式。也就是说,表达的就是Γ⊃(B⊃A)。随着更多条件的加入,如Δ的加入,图5是标准记法Δ⊃(Γ⊃(B⊃A))表达的意思。如果这样的方式就是概念文字条件句的读法,那么弗雷格二维记法的逻辑理由无非是让我们省略了括号而已。

通常的理解与弗雷格早期逻辑中的理解一样,一个带有多个条件的概念文字句子具有固定的逻辑结构。读法按照下述规则进行:从左上方开始,沿着横线往右,直到遇到第一条条件句竖线,该竖线右边的内容都跟在“如果”后面,然后说“那么”,再继续。这一规则对于一个条件本身也是条件句的情形可以递归地使用。但是对于一个具有这种结构的句子,也未必一定具备让人信服的理由来使用上述二维表示方式。很明显,弗雷格知道他的概念文字条件句可以有多种读法。我们在前面已经看到,(R⊃(Q⊃P))可以表示成图4中的概念文字。弗雷格认为由此产生的句子仅仅是表示P、Q和R处于一种逻辑关系之中,这种关系可以用不同的方式读出来。在这一句子中,我们可以把“—P”称为“主要成分”,而把“—Q”和“—R”称为“次要成分”;然而,我们也可以把图5视为主要成分而单独把“—R”视为次要成分。在前一种情形下,这个句子读成条件句“如果R和Q,那么P”;而在后一种情形下,则读成“如果R,那么,若Q则P”。这一概念文字句子本质上是二维的,与此相应的是一族可证等值的系列有序的线性结构。
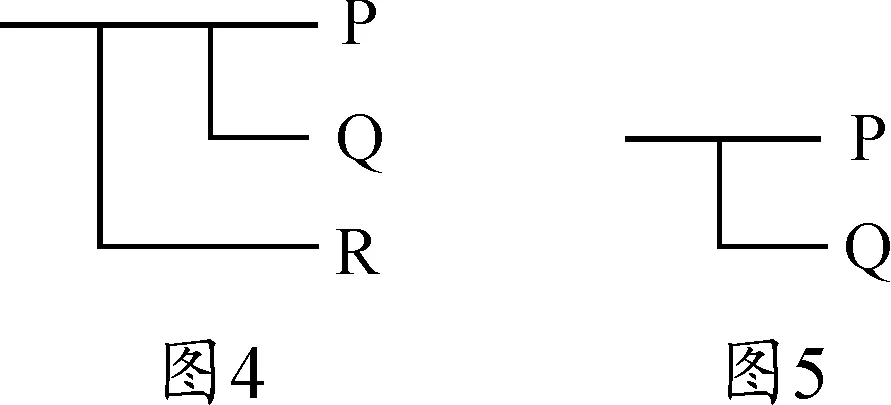
按照弗雷格的意思,可证等值的句子表达的是一个相同的思想。逻辑所关心的则是所有等值命题都拥有同一思想,因此对于每一个等值命题系统来说,单个标准命题就够了。弗雷格的二维记法为多于一个条件的条件句提供的刚好就是这样的标准命题。在我们现在的标准线性记法中,每一个句子有且仅有一个主联接词,这一联接词也是推导规则应用之处;概念文字的句子则相对于分析来讲也只有一个主联接词。图6中的句子有4种不同的读法。一种读法是把“—S”作为次要成分,而在余下的主要成分中,再把R作为其次要成分;这就表达成现在的公式S⊃(R⊃(Q⊃P))。当把“—S”作为次要成分,把主要成分中的“—P”作为其主要成分,其余作为次要成分的时候,得到的公式将是S⊃((R & Q)⊃P)。第三种则是把“—S”和“—R”看成是次要成分而得出(S & R)⊃(Q⊃P)。还有一种就是把“—S”“—R”和“—Q”都处理成次要成分,“—P”为主要成分,得到的是((S & R & Q)⊃P);在这种情况下,主联接词就是上面横线最右边那段。
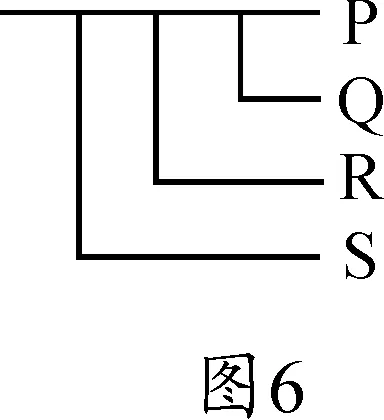
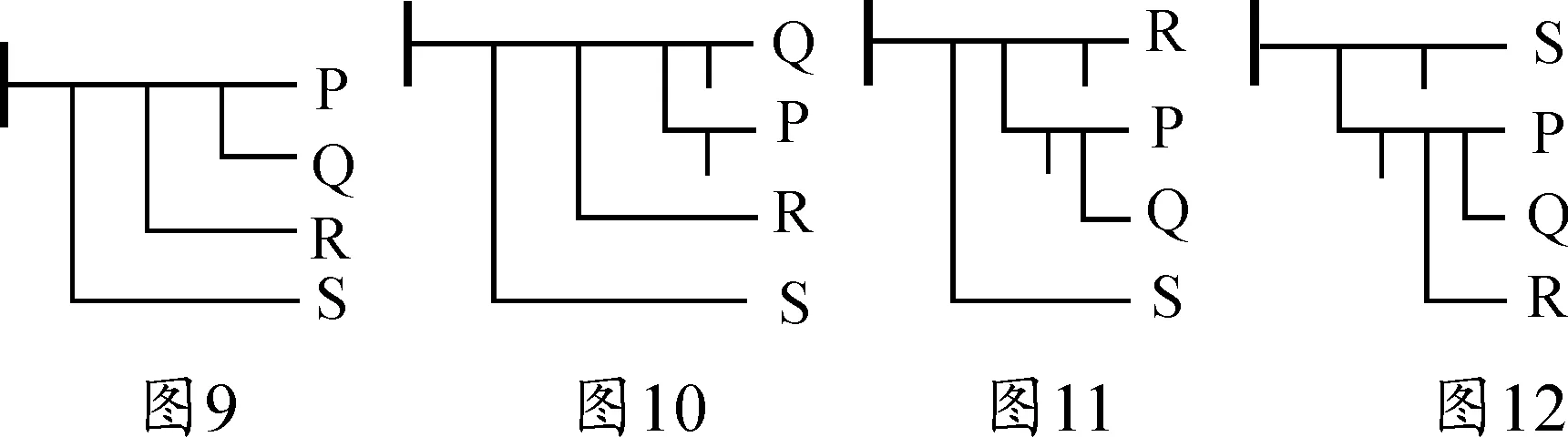
公式S⊃(R⊃(Q⊃P))是说,或者前件S为假,或者后件R⊃(Q⊃P)为真。这一思想由图6中的概念文字句子来表达。但是,在我们的读法中,它没有说或者S为假或者R⊃(Q⊃P)为真;它展示的却是4个句子S、R、Q和P之间一个复杂的逻辑关系,这一关系可以分析成或者S为假或者R⊃(Q⊃P)为真,当然也可以用其他方式来分析。在这个表达式中,横线与左边的条件句竖线一起构成了一个复杂的句子联接词,它作为一个单位起作用,就像“2+3=5”的“+”和“=”一起作为一个单位表示了2、3与5之间的一种算术关系。因此,与马蹄号不同,弗雷格的条件句竖线可以是一个n元的句子联接词,不管其复杂度是多少。因此,图7展示的是句子之间的一种逻辑关系,同样,图8也展示了句子之间的一种逻辑关系。也就是说,在弗雷格的记法中,交换次要成分是允许的;改变次要成分的顺序需要合理证明,这也是次要成分的交换在《算术基础》中作为一条规则提出来的原因,也是在《概念文字》中作为一条定理被证明的原因。但是,在弗雷格的记法中,这样一条规则可以涵盖所有这种形式的情形。因此,弗雷格的条件句竖线把“逻辑完美性和最大简洁性”组合起来,把“极大的逻辑精确性和明晰性、简洁性”组合起来。弗雷格逻辑中的换质位规则有力地支持了这一点:对图9中的判断应用换质位规则,将得到图10或者图11、图12。

但是,在我们现在的标准线性记法中,一个句子不能有不同的看法;一个复合句有且只有一个主联接词,而组成这个复合句的句子则至多只有一个主联接词。因此,S⊃(R⊃(Q⊃P))与S⊃(﹁(Q⊃P)⊃﹁R)等值的自然推演证明,以及S⊃(R⊃(Q⊃P))与S⊃(﹁P⊃(Q⊃﹁R))等值的自然推演证明,这两者是完全不同的。前者看起来是换质位规则的一次应用即可以得到,而后者则不然。在《概念文字》中,一个多重条件的条件句对应着标准线性记法公式的一个等价类。弗雷格也认为同一个思想可以有不同的方式表达出来,图13、14、15三个句子表达的是同一个思想,仅仅是形式不同而已。

二、概念文字和存在图:信息处理
弗雷格的记法与《形式的规律》的开关电路理论有相近之处。《形式的规律》是英国数学家斯宾塞·布朗于1969年出版的,书中用数学形式解释哲学中的思维现象。正文的第一页引用了中国古代哲学家老子的话“无名天地之始”[3]1,一切论证便从这里开始。现在把弗雷格的系统和《形式的规律》联系起来进行讨论。
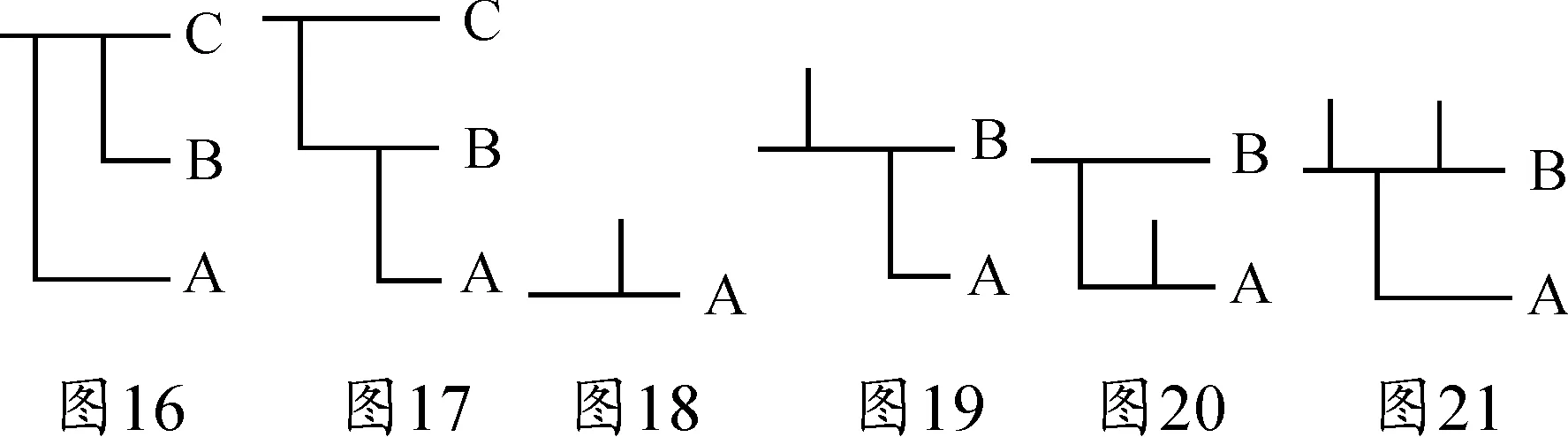
在B⊃A中,这一连续记法从结构上把这些命题和树形式联系了起来。我们现在把A⊃(B⊃C)(图16)和(A⊃B)⊃C(图17)的概念文字做一个比较:概念文字的不同树形结构把蕴涵的非交换性图示出来。在概念文字中,否定用一条竖线图示出来,图18是﹁A的概念文字句子,否定号“否定”的是其右边所有的内容。现在,我们在使用弗雷格记法的时候会遇到困难。逻辑并非只是蕴涵的结构,它还必须处理其他联接词如“并且”“或者”以及由否定引起的各种方式。图19的概念文字句子表示的是﹁(A⊃B),图20则表示(﹁A)⊃B。按照标准逻辑,A∨B、A & B分别表示成图20、21的概念文字句子,于是逻辑关系在二维记法中变成了空间关系,图形越来越复杂了。
1957年已经有人在逻辑杂志上提出过弗雷格图形与开关电路之间的一个早期的联系[6]。我们现在把弗雷格的图看作是字母位于右边的信号处理器。在图22中,信息流从右往左通过,图形最左边的边表示图形本身的表达式的值,Z是A、B、C和D经过转换后图形的值。因此,在图23中,A在表示否定的竖线的作用之下转换成﹁A。而对于蕴涵式,我们有结果﹁A∨B(图24)。


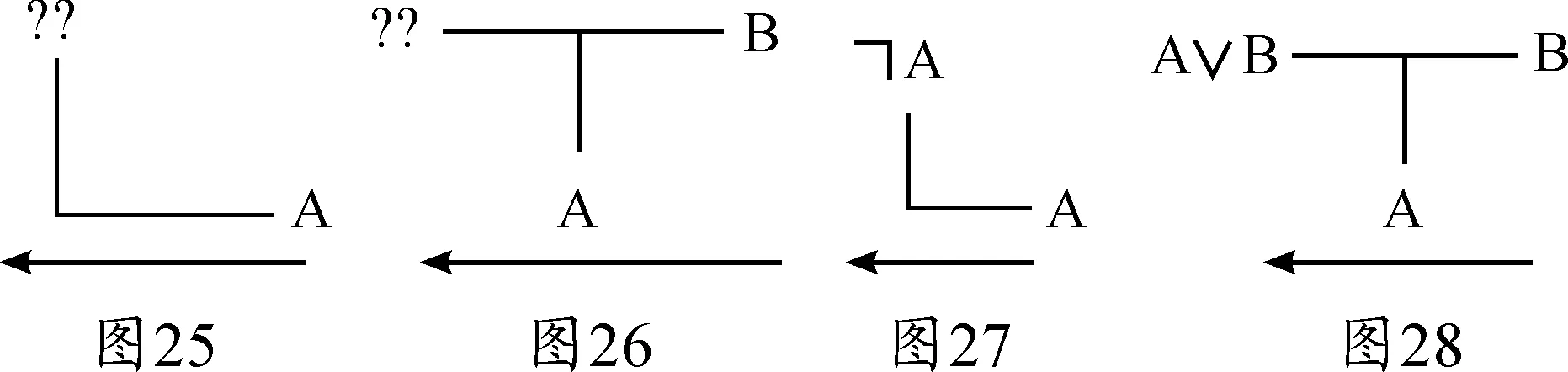
但是,当拐弯的时候(图25),信号怎么办呢?另外,在树中把两条线简单地连接起来(图26)又是一种什么样的行为呢?答案是简单的,而且这一答案揭示的是弗雷格图形的一种句法基础,这一句法使得这些图形便于使用:(1)当内容线拐弯的时候,信号被否定(图27);(2)两条线的连接执行的是运算“或者”(图28)。现在,信号就可以在弗雷格的形式系统中流动,弗雷格的语言得到了新生。在这些运算指派下,弗雷格的图形变成了信息处理网络,它们在“并非”和“或者”这一语言中非常容易读出来。
在斯宾塞·布朗的《形式的规律》中,直角是一个标记、一个包含者、一个原始区分的代表;A⊃B写成图29,而图30、图31、图32是弗雷格记法和斯宾塞·布朗记法的混合。

美国数学家、信息论创始人克劳德·香农(Claude Shannon)于1930年代发现了布尔代数和开关网络之间的联系。皮尔士发现的图式逻辑系统包括他的推演指号以及存在图[7]。皮尔士的图式系统与我们这里讨论的主题密切相关,他的推演指号也是由一个直角构成的(图33)。
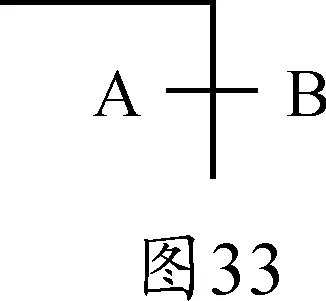
这一指号是一个由否定(上横线)和加(+,逻辑上的“或者”)组合而成的指号,它可以分解如下:
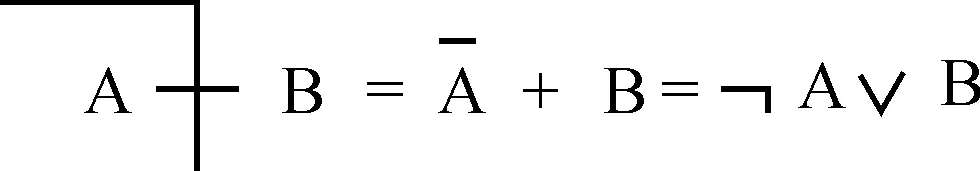
皮尔士试图通过这个组合指号来调动其整个指号理论。与弗雷格的蕴涵图形一样,皮尔士的推演指号指出了这一运算的一个整体意义,而且提示了与其他逻辑运算相互关系。在弗雷格蕴涵图中,通过在直角那里发现“否定”以及在联接点发现的“或者”,我们可以看到弗雷格蕴涵图与皮尔士推演指号及其内部结构之间的类似之处,而弗雷格图形和皮尔士图形之间的这些类似还值得进一步研究。
参考文献:
[1]RUSSELL B.Principle of Mathematics[M].Cambridge :Cambridge University Press,1903.
[2]FREGE G.Conceptual Notation and Related Articles[M].Oxford:Clarendon Press,1972.
[3]SPENCER-BROWN G.Laws of Form[M].[S.l.]:Allen & Unwin,1969.
[4]弗雷格.弗雷格哲学论著选辑[M].王路,译.北京:商务印书馆,2006.
[5]FREGE G.Posthumous Writings[M].Chicago :University of Chicago Press,1979.
[6]HOERING W.Frege und die Schaltalgebra[J].Archive for Mathematical Logic,1957,3(3/4):125-126.
[7]PEIRCE C S.Collected Papers vol.4[M].Cambridge:Harvard University Press,1933.
(责任编辑张佑法)

引用格式:赵亮英.语境、意向与指称——塞尔与马蒂尼奇的意向指称理论之比较[J].重庆理工大学学报(社会科学),2015(12):25-30.
Citation format:ZHAO Liang-ying.Context, Intention and Reference: Comparative on Searle and Martinich’s Intentional Theory of Referring[J].Journal of Chongqing University of Technology(Social Science),2015(12):25-30.

