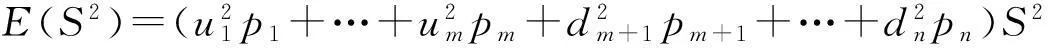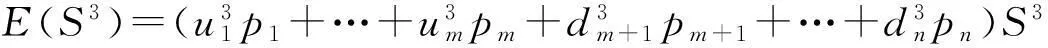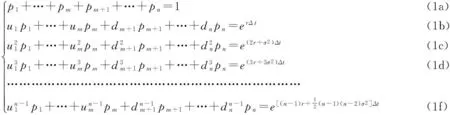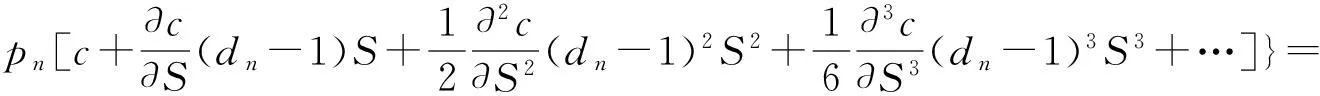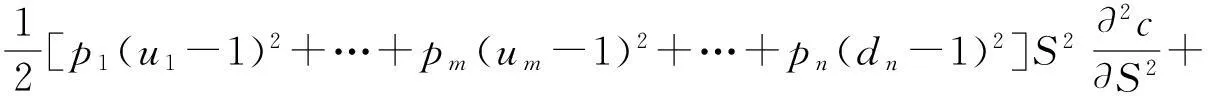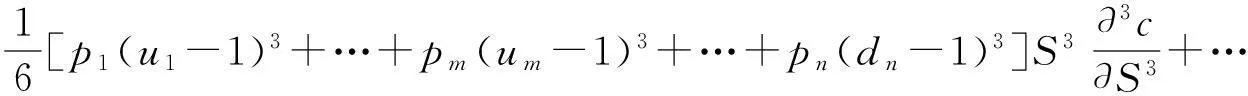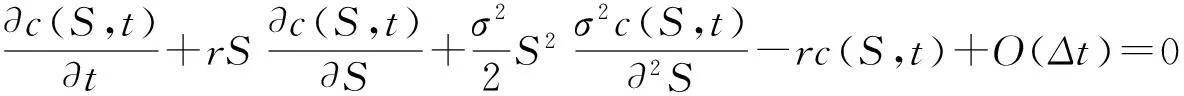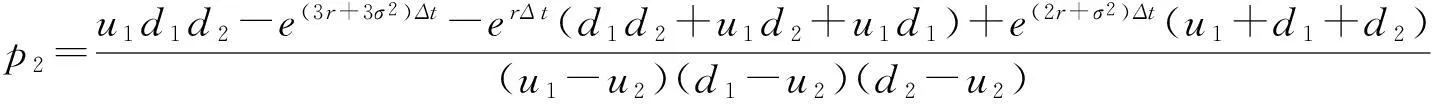期权定价的n叉树模型

范宏高

(武汉大学 数学与统计学院,湖北 武汉　430072)

期权定价的n叉树模型

范宏高

(武汉大学 数学与统计学院,湖北 武汉430072)

摘要：在风险中性假设的基础上,将三叉树期权定价公式推广到n叉树公式,并证明了n叉树公式近似满足Black-Scholes方程.最后以四叉树为例,使用R程序说明了n(n≥4)叉树与三叉树相比,计算效率更高,计算结果更精确.

关键词：n叉树;四叉树;Black-scholes方程

中图分类号：F830

文献标识码：A

文章编号：1009-2714(2015)04- 0016- 04

doi:10.3969/j.issn.1009-2714.2015.04.004

收稿日期：2015—09—02

作者简介：范宏高(1990—)，男，湖北荆州人，硕士，主要研究方向为金融统计.

期权定价的方法有许多种,其中以二叉树图法最为直观与简单,它是标的资产价格连续时间模型的一种离散形式.从1986年开始,一些学者又开始了对三叉树定价的研究,并取得了一些进展.明显地,运用三叉树研究期权价格比二叉树研究的结果更准确、更好.自然要问的问题是，能否用四叉树、五叉树…n叉树来研究期权价格？

本文沿用了三叉树模型的思路，剔除了对称性条件ud=1，使得风险资产价格上涨与下降比例更加自由。在此假设下给出了n叉树定价模型，并证明了它以一阶时间精度满足Black-Scholes方程.最后我们详细地讨论了四叉树的定价公式并给出了一个数值计算实例，说明了n叉树(n≥4)定价模型比三叉树近似效果更好.

1n叉树定价模型

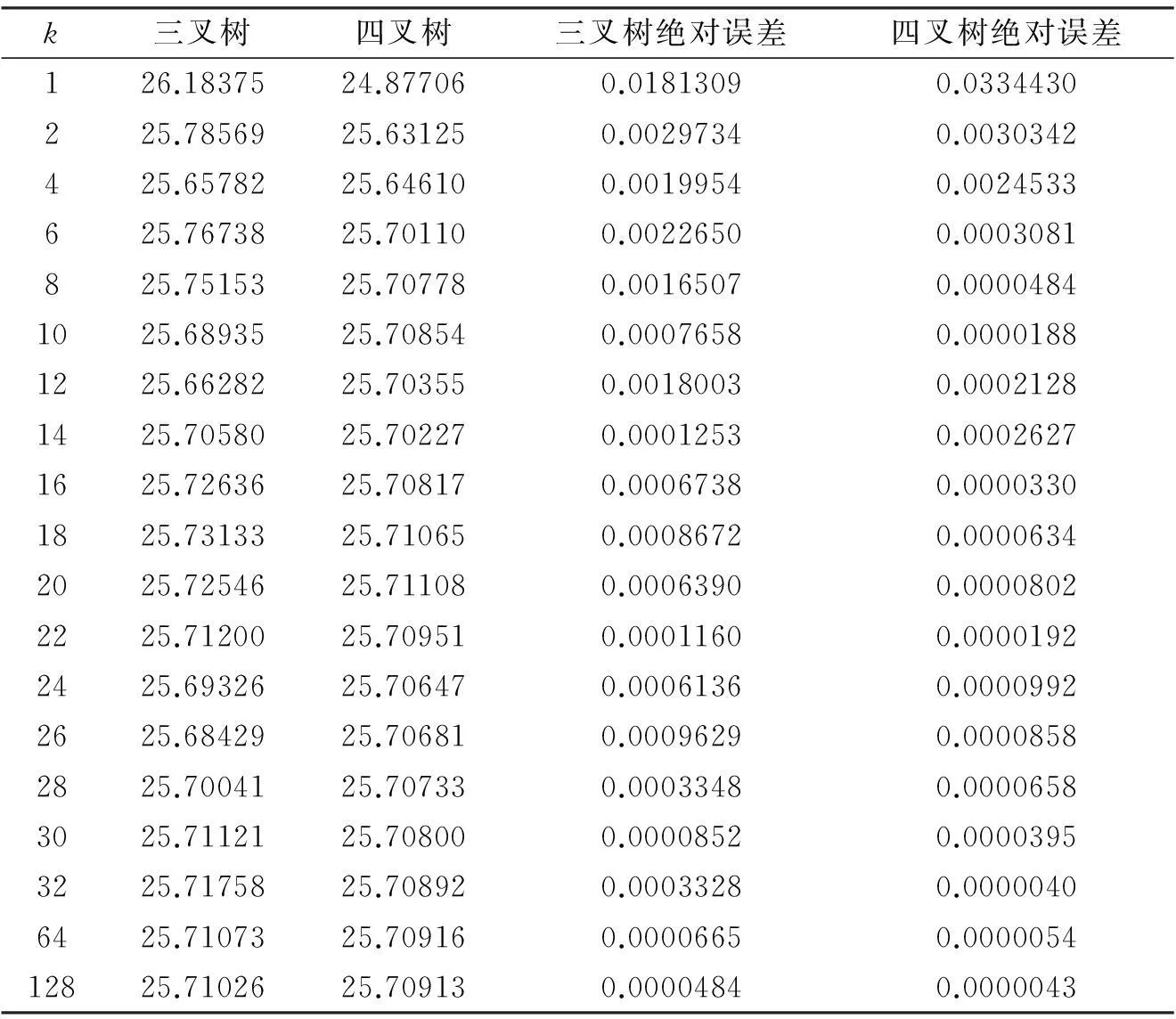
下面我们建立实物期权n叉树定价模型.设在时刻t到时刻t+Δt内，风险资产S有n种变化状态：上升到u1S,…,umS，或下降到dm+1S,…,dnS，其概率分别为p1,…,pm,pm+1,…,pn，其中u1,…,um,dm+1,…,dn全不相等且m

E(S)=(u1p1+…+umpm+dm+1pm+1+…+dnpn)S

……………………………………………………………

于是，建立线性方程组

(1)

在此线性方程组中：

1)系数行列式为范德蒙行列式，u1,…,um,dm+1,…,dn全不相等，因而系数行列式不为0，则方程组存在唯一解.

2)下面证明此模型给出的期权定价公式是以一阶时间精度满足Black-Scholes方程。

当给定ui与dj,i=1,…,m;j=m+1,…,n．考虑当Δt→0 时，n叉树公式的极限

c=e-rΔt[p1Cu1+…+pmCum+pm+1Cdm+1+…+pnCdn]

(2)

其中，Cui和Cdj分别看涨期权到期时的价格，c为看涨期权价格，Cui=max(uiS-X,0) ，Cdj=max(djS-X,0),i=1,…,m;j=m+1,…,n,X为期权的执行价格.

下面证明该渐近的极限是Black-Schole方程的解，由于n叉树是网格函数，因此必须将其延拓为连续函数，使得两个函数在网格点上相等[2]，n叉树的连续模拟可以表示为

c(S,t-Δt)=e-rΔt[p1c(u1S,t)+…+pmc(umS,t)+…+pnc(dnS,t)]

(3)

上式可以改写成

-c(S,t-Δt)+e-rΔt[p1c(u1S,t)+…+pmc(umS,t)+…+pnc(dnS,t)]=0

(4)

为方便起见，取当前的时刻为t-Δt,记c=c(S,t),假设c(S,t)足够光滑，对上式在点(S,t)泰勒展开，得

要证明n叉树期权定价公式近似服从Black-Scholes方程，只需证明下面的等式成立:

e-rΔt[p1(u1-1)+…+pm(um-1)+…+pn(dn-1)]=rΔt+O(Δt2)

(5)

e-rΔt[p1(u1-1)2+…+pm(um-1)2+…+pn(dn-1)2]=σ2Δt+O(Δt2)

(6)

e-rΔt[p1(u1-1)3+…+pm(um-1)3+…+pn(dn-1)3]=O(Δt2)

(7)

事实上，

1)由e-rΔt[(1b)-(1a)]知

e-rΔt[p1(u1-1)+…+pm(um-1)+…+pn(dn-1)]=1-e-rΔt=rΔt+O(Δt2)

2)由e-rΔt[(1e)-2×(1b)+(1a)]知

e-rΔt[p1(u1-1)2+…+pm(um-1)2+…+pn(dn-1)2]=

e-rΔt+e(r+σ2)Δt-2=σ2Δt+O(Δt2)

3)由e-rΔt[(1d)-3×(1c)+3×(1b)-(1a)]知

e-rΔt[p1(u1-1)3+…+pm(um-1)3+…+pn(dn-1)3]=

e(2r+3σ2)Δt-3e(r+σ2)Δt-e-rΔt+3=O(Δt2)

将以上结果代入泰勒展开式，化简得

-c(S,t-Δt)+e-rΔt[p1c(u1S,t)+…+pmc(umS,t)+…+pnc(dnS,t)]=

由于c(S,t)满足n叉树上式，因此得到

当Δt→0时，由n叉树模型得到的c(S,t)满足Black-Scholes方程，即n叉树公式以一阶时间精度满足Black-Scholes方程，至此，已经证明了n叉树定价模型的可行性。

3四叉树定价模型

取n=4，建立四叉树期权定价模型。设在时刻t到时刻t+Δt内，风险资产S有四种变化状态，S上升到u2S，u1S或下降到d1S,d2S,其中u2>u1>1>d1>d2,其概率分别为p2,p1,q1和q2，同时，根据期望的定义，在时刻t+Δt有

E(S)=(u2p2+u1p1+d1q1+d2q2)S

(8)

于是我们可以建立如下线性方程组

(9)

解此线性方程组，得

(10)

当期权的到期期限为T，执行价格为X时，四叉树期权定价公式为

此时，可以应用四叉树定价公式来计算期权价格。

4实例

假设股票价格S=120，执行价格X=100，波动率σ=0.25,无风险利率r=0.1，到期期限T=0.5，我们可以用连续的Black-Scholes公式，计算出该看涨期权的价格为c=25.70902，利用R程序计算出三叉树与四叉树定价模型的价格，结果如表1所示：

表1　三叉树与四叉树定价模型的比较

从表1可以看出：当k超过一定的值时，四叉树定价的绝对误差远远小于三叉树的绝对误差，并且当k逐渐增大的时候，四叉树以更快的速度近似于Black-Scholes公式计算的价格。

参考文献:

[1]丁正中，曾慧.实物期权的三叉树定价模型[J]．统计与决策，2005，22(11)：5～7．

[2]Kwok Yue-Kuen.Mathematical Models of Financial Derivatives[M].Singapore:Springer Verlag:199~200.

[3]何颖俞.美式期权的三叉树定价模型[J].黑龙江大学自然科学学报，2008,25(01):83~84.

The n-ary tree option pricing model

FAN Hong-gao

(School of Mathematical and Statistics,Wuhan University, Wuhan430072,China)

Abstract:In this paper, we generalize the trinominal tree option pricing figure to the n-ary tree on the risk neutral hypothesis and prove it satisfying Black-Scholes equation approximately. Finally, it is shown that the n-ary tree (n≥4) is better than the trinominal tree through a quadtree example by the method of R project.

Key words:the n-ary tree ; the quadtree; Black-Scholes equation