Hilbert空间A-可因子分解算子的性质

王励冰　（河南省周口师范学院数学与统计学院　466001）

王超杰　（河南省永城市高级中学　476600）

Hilbert空间A-可因子分解算子的性质

王励冰（河南省周口师范学院数学与统计学院466001）

王超杰（河南省永城市高级中学476600）

摘要：在已有A-可因子分解算子概念的基础上，建立了A-可因子分解算子是有界的若干充要条件，同时讨论了其对偶算子的性质。

关键词：A-可因子分解算子对偶算子有界

DOI：

作者简介：

10.16657/j.cnki.issn1673-9132.2016.01.017

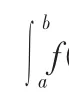
首先列出A-可因子分解算子的定义。

定义1[3]设1≤p≤∞，线性算子L：L2（Rd）→LP（E）(E为Rd的一个可测子集)。如果对于任意可因子分解函数f=准g，其中f，g∈L2（Rd），准是Rd上以ZdA为周期的函数，算子L具有下列形式

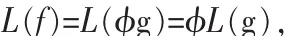
那么称算子L为A-可因子分解算子。

下面给出A-可因子分解算子的两个性质。

定理1[3]算子L：L2（Rd）→L1（Q0）是有界A-可因子分解算子当且仅当存在g∈L2（Rd），使得L（f）=（f，g）A（t），坌f∈L2（Rd）。更多地，||L||=||g||。

引理1[3]设A-可因子分解算子L1，L2：L2（Rd）→L1（Q0），则L1=L2当且仅当

现在接着讨论A-可因子分解算子的性质，首先给出A-可因子分解算子是有界的三个充要条件。

定理2设L：L2（Rd）→L2（Q0）是线性A-可因子分解算子，则L是有界的当且仅当存在常数B>0（B=||L||），使得对坌f∈L2（Rd）有

|L（f）（t）|≤B||f||A（t），a.e. t∈Q0。

更多的，L是同构算子当且仅当存在常数A，B>0（A=||L-1||-1，B=||L||）使得对任意的f∈L2（Rd）有

A||f||A（t）≤|L（f）（t）|≤B||f||A（t），a.e. t∈Q0。

证明对Rd上任意有界ZdA周期函数准和坌f∈L2（Rd）有

所以由引理1可得结论。

综上所述，定理2、定理3和定理4建立了A-可因子分解算子是有界的充要条件，于是可以用这三个定理来判定A-可因子分解算子的有界性，定理5对A-可因子分解算子L的对偶算子L*进行了讨论，给出了对偶算子L*的一个性质。

参考文献：

[1]张恭庆，林源渠．泛函分析讲义[M]．北京:北京大学出版社，2003．

[2]夏道行，吴卓人．实变函数论与泛函分析[M]．北京:高等教育出版社，2010．

[3]王励冰，王超杰．Hilbert空间A-可因子分解算子[J]．科技展望，2015，25(17)：265．

[4]王励冰，王超杰．A-内积及其性质[J]．佳木斯职业学院学报，2015（2）：240-241．

[5]李登峰，薛明志．Banach空间上的基和框架[M]．北京:科学出版社，2007．

王励冰(1986- )，男，河南省周口人，助教，硕士研究生，主要从事小波分析及其应用方面的研究。

（责编赵建荣）