正交各向异性矩形板的自由振动特性分析

曾军才， 王久法， 姚　望， 于　涛

(1.中国船舶重工集团公司第七一○研究所，湖北 宜昌　443003; 2.上海帝西恩精密工具有限公司，上海　200137)



正交各向异性矩形板的自由振动特性分析

曾军才1， 王久法1， 姚望2， 于涛2

(1.中国船舶重工集团公司第七一○研究所，湖北 宜昌443003; 2.上海帝西恩精密工具有限公司，上海200137)

正交各向异性矩形板越来越广泛应用于航空、航天、船舶和车辆等各种现代工程中，由于其在各个方向上具有不同力学性质，原有的各向同性板理论已不适用，因此对其振动特性的研究具有重要的工程应用价值和理论价值。近年来，许多学者进行了大量研究，取得了一系列成果。正交各向异性板的求解方法主要为数值方法，如Reyleigh-Ritz法[1]，微分求积法[2]和有限元法[3]等方法；也有一些学者使用解析解进行求解，如Gorman[4]用叠加法，Kshirsagar等[5]使用无截断无穷级数的叠加原理，Hurlebaus等[6]基于Galerkin原理，张承宗等[7]用复级数展开法，Huang等[8]使用Green函数法，黄炎等[9]和Xing等[10]采用分离变量法，Bercin等[11]用Kantorovich法，Sakata等[12]和Rahbar Ranji等[13]使用延拓Kantorovich法分析了正交各向异性板的自由振动特性。不过这些解析法研究的矩形板的边界条件都是经典的边界条件，而对于更符合工程实际的弹性边界条件却很少涉及。

近年来，Li等[14-15]提出了一种改进的Fourier级数方法进行了板梁结构的自由振动分析，通过将板梁结构的位移函数表示为傅里叶余弦级数和辅助多项式或者辅助级数的线性组合，使得弹性约束边界条件能够得到精确满足。

本文采用改进Fourier级数的方法，将正交各向异性矩形薄板的位移函数表示为标准的二维Fourier余弦级数和辅助Fourier级数之和的形式。结合Kirchhoff理论，建立了矩形板在任意边界条件下的自由振动模型，推导出与控制方程等价的矩阵表达式，板结构的振动模态可以通过求解矩阵特征值而得到。最后通过数值仿真，验证了本文方法的准确性和快速收敛性。

1控制微分方程求解

本文所研究的正交各向异性矩形板的模型如图1所示，板结构的四个边界处分别均匀地布置横向位移弹簧和旋转约束弹簧，通过改变刚度值，实现对任意弹性边界条件的模拟。所有的经典边界条件都能够通过将弹簧系数设置为无穷大或零来简单地获得。例如将四边的横向位移约束弹簧刚度值和旋转约束弹簧刚度值同时设置为无穷大，就相当于模拟了四边固支的边界条件。

图1　任意边界条件下板结构示意图Fig.1 A plate with general elastic boundary support

根据薄板振动理论，各向异性矩形板自由振动的控制方程为：

(1)

式中：D1=E1h3/[12(1-v1v2)]，D2=E2h3/[12(1-v1v2)]，D3=D12+2D66，D12=v1D2=v2D1，D66=G12h3/12，w为挠度，ρ为密度，h为厚度，E1、E2、v1、v2和G12为板的弹性常数，ω为角频率。

弯曲振动的位移场可以通过沿x和y轴方向的两个分量来描述，本文中，位移采用二维改进傅里叶级数展开来表示：

(2)

式中：λm=mπ/a，λn=nπ/b，Amn、clm、dln分别为用来描述板结构弯曲振动未知的Fourier系数和辅助级数的系数。与x相关的辅助函数分别表示为：

(3)

(4)

(5)

(6)

与y相关的辅助函数可以将式(3)-(6)中的a和x分别用b和y进行替换得到。通过辅助级数的引入，解决了振动位移导数在边界不连续的问题。从而此位移函数可以同时满足位移边界条件和力的边界条件。这种改进的傅里叶级数解能适用于任意的弹性边界条件，同时也能改善级数的收敛性。

将式(2)代入式(1)中有：

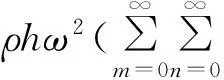
(7)

将所有的辅助级数及其导数均展开为Fourier余弦级数，并利用方程左右两端余弦项系数相等有：

(8)

式中：m=0,1,2,…,n=0,1,2,…，辅助级数及其导数的Fourier展开为：

(9)

(10)

当所有级数展开在数值计算过程中均截断于m=M和n=N，方程(8)可以写为如下矩阵形式：

(BA+CP)-ρhω2(EA+FP)=0

(11)

式中：A=[A00,A01,…,A0N,A10,A11,…,A1N,…,AM0,AM1,…,AMN]，P=[c10,c11,…,c1M,c20,c21,…,c2M,…c40,c41,…,c4M,d10,d11,…,d1N, …,d40,d41,…,d4N] 。

2弹性约束边界条件

根据薄板理论，弹性约束边界条件写为：

在y=0上,

(12)

(13)

在y=b上,

(14)

(15)

在x=0上,

(16)

(17)

在x=a上,

(18)

(19)

式中：kx0和Kx0(kxa和Kxa)分别表示x=0(x=a)处横向位移和旋转约束弹簧刚度，ky0和Ky0(kyb和Kyb)分别表示y=0(y=b)处横向位移和旋转约束弹簧刚度。

将式(2)代入式(12)~(19)中，并将辅助级数展开Fourier级数，由方程两端余弦项系数相等有：

(20)

(21)

(22)

(23)

上面四个式子中，m=0,1,2,…。

(24)

(25)

(26)

(27)

式(24)~(27)中，n=0,1,2,…。

当级数的截断数取为m=M和n=N时，式(20)-(27)可写成矩阵表达示为：

ΗP=QA

(28)

将式(28)代入式(11)中，可得到最终的系统方程为

[K-(ρhω2/D1)M]A=0

(29)

式中：K=(B+CH-1Q)/D1，M=(E+FH-1Q)。

通过求解这一标准和矩阵特征值即可得到正交各向异性矩形板的固有频率和特征向量，每阶特征向量为所对应结构模态形状分布的Fourier系数。

3数值结果与讨论

文中用C表示固支边界条件，F表示自由边界条件，S表示简支边界条件。为了验证本文方法的准确性，表1给出了不同长宽比和边界条件下矩形薄板的前六阶无量纲频率参数Ω=ωa2(ρh/D1)1/2，矩形板的弹性参数为D2=0.5D1,D3=0.5D1。表中SSSS表示沿边界x=0，y=0，x=a和y=b的边界条件都为简支，简支边界条件可通过设置横向位移约束弹簧刚度值为无穷大，旋转约束弹簧刚度值为零，在本文中，无穷大取为107×D1。同时表中也给出了文献[12]中采用延拓Kantorovich法得到的结果；表2给出了弹性参数为D2=D1,D3=0.5D1的矩形薄板在不同长宽比和边界条件下的无量纲频率参数，同时也给出了文献[10]通过分离变量法得到的计算结果。通过比较可以发现本文方法得到的结果与其它方法得到的结果吻合良好，在本文计算过程中，两个方向的位移展开采用相同的截断数，取值为M=N=14。同时，图2给出了采用本方法得到的D2=D1,D3=0.5D1的矩形薄板在a/b=1时的前四阶固有振型图。

表1　 D2=0.5D1, D3=0.5D1时矩形板频率的频率参数

表2　 D2=D1, D3=0.5D1时矩形板频率的频率参数

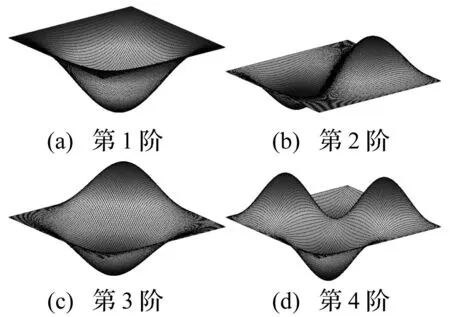
图2　SSCC矩形板前四阶的振型Fig.2 The first four mode shapes for the SSCC rectangular plate

为了检验本文方法的收敛性，表3给出了各向异性矩形薄板在不同截断数时的计算结果，板的长宽比a/b=1，弹性参数为D2=D1,D3=0.5D1，边界条件为CCCC。从表中可以看出，M=N=5和M=N=20时得到的前八阶无量纲固有频率的最大偏差为0.22%，即本方法具有较好的收敛性，当截断数取较小的值时就能得到比较精确的结果。

本文方法不仅可以计算经典边界条件下矩形薄板的振动频率，而且适用于弹性支撑的矩形板。表4给出了长宽比a/b=1的正交各向异性矩形薄板在不同弹性支撑刚度下的前8阶无量纲振动频率曲线。x=0和x=a上旋转约束弹簧刚度值都为无穷大，y=0和y=b上旋转约束弹簧刚度值都为零，而四边上的横向位移约束弹簧刚度值都为10k×D1。从表中可以看出，随着弹簧刚度值的增加，矩形板的频率也随之增大，当k≥5时，数值几乎不在变化，频率值变为边界条件为CSCS下的结果。从这里也能看出，本文看中刚度值无穷大取为107×D1是合适的。

表3　正交各向异性矩形板频率的收敛性

表4　 弹性边界条件下板的振动频率

4结论

(1) 本文采用横向位移约束弹簧和旋转约束弹簧来模拟任意的弹性边界条件，所有经典的边界条件都可以通过设置四边上的弹簧刚度值为无穷大或者零来模拟。

(2) 文中采用改进Fourier级数法建立了正交各向异性矩形薄板的自由振动模型，得到了板结构固有频率的解析解。振动位移函数表示为一个标准的二维Fourier余弦级数和辅助级数的线性叠加。通过辅助级数的引入，解决了振动位移的导数在边界潜在的不连续性问题，从而使改进Fourier级数法适用于任意弹性边界条件下的矩形板。

(3) 本文方法中，所有的频率参数可以通过求解一个标准的特征值问题而得到。对于不同边界条件下的模态参数，只需设置相应的边界弹簧刚度值，然后就可以通过统一的程序进行求解。

(4) 最后进行了数值分析，并与其它文献的结果进行了比较，验证了本方法的快速收敛性和准确性。

参 考 文 献

[1] Bhat R B.Natural frequencies of rectangular plates using characteristic orthogonal polynomials in the Rayleigh-Ritz method [J]. Journal of Sound and Vibration, 1985, 102(4):493-499.

[2] Jafari A A,Eftekhari S A. An efficient mixed methodology for free vibration and buckling analysis of orthotropic rectangular plates [J]. Applied Mathematics and Computation, 2011, 218:2670-2692.

[3] Bardell N S, Dunsdon J M, Langley D S.Free vibration analysis of thin coplanar rectangular plate assemblies-Part I: theory, and initial results for specially orthotropic plates[J]. Composite Structures, 1996, 34:129-143.

[4] Gorman D J. Accurate free vibration analysis of clamped orthotropic plate by the method of superposition[J]. Journal of Sound and Vibration, 1990, 140:391-411.

[5] Kshirsagar S, Bhaskar K.Accurate and elegant free vibration and buckling studies of orthotropic rectangular plates using untruncated infinite series [J]. Journal of Sound and Vibration, 2008, 314:837-850.

[6] Hurlebaus S, Gaul L, Wang J T S.An exact series solution for calculating the eigenfrequencies of orthotropic plates with completely free boundary [J]. Journal of Sound and Vibration, 2001, 244(5):747-859.

[7] 张承宗，杨光松. 各向异性板结构横向弯曲一般解析解[J]. 力学学报, 1996, 28(4):429-440.

ZHANG Cheng-zong, YANG Guang-song.General analytic solutions for transverse bending problem of anisotropic plate structures [J]. Acta Mechanica Sinica, 1996, 28(4):429-440.

[8] Huang M, Ma X Q, Sakiyama T, el al.Free vibration analysis of orthotropic rectangular plates with variable thickness and general boundary conditions [J], Journal of Sound and Vibration, 2005, 288:931-955.

[9] 黄炎，廖瑛，谢燕. 双参数弹性地基上受压的正交异性板的自由振动[J]. 工程力学, 2006, 23(3):46-49.

HUANG Yan, LIAO Ying, XIE Yan. Free vibration of compressed orthotropic plate on two parameter elastic foundation [J]. Engineering Mechanics, 2006, 23(3):46-49.

[10] Xing Y F, Liu B. New exact solutions for free vibrations of thin orthotropic rectangular plates [J]. Composite Structures, 2009, 89:567-574.

[11] Bercin A N.Free vibration solution for clamped orthotropic plates using the Kantorovich method[J]. Journal of Sound and Vibration, 1996, 196(2):243-247.

[12] Sakata T, Takahashi K, Bhat R B.Natural frequencies of orthotropic rectangular plates obtained by iterative reduction of the partial differential equation [J]. Journal of Sound and Vibration, 1996, 189(1):89-101.

[13] Rahbar Ranji A, Rostami Hoseynabadi H.A semi-analytical solution for forced vibrations response of rectangular orthotropic plates with various boundary conditions[J]. Journal of Mechanical Science and Technology, 2010, 24:357-364.

[14] Li W L. Free vibrations of beams with general boundary conditions [J]. Journal of Sound and Vibration, 2000, 237(4):709-725.

[15] Li W L, Zhang X F, Du J T. An exact series solution for the transverse vibration of rectangular plates with general elastic boundary supports [J]. Journal of Sound and Vibration, 2009,321(1/2):254-269.

[16] 史冬岩，石先杰，王青山,等. T型耦合板结构振动特性研究[J]. 振动与冲击, 2014, 33(4): 185-189.

SHI Dong-yan,SHI Xian-jie,WANG Qing-shan,et al. Vibration analysis of a T-coupled plate structure [J].Journal of Vibration and Shock,2014,33(4):185-189.

第一作者 曾军才 男，高级工程师，1980年10月生

摘要：采用改进Fourier级数方法，建立了正交各向异性矩形薄板的弯曲振动模型，推导出与振动控制方程等价的矩阵方程，得到控制方程在任意边界条件下的解析解。弯曲振动的位移函数表示为标准的二维Fourier余弦级数和辅助Fourier级数之和，通过辅助级数的引入，解决了振动位移函数的偏导数在各边界处潜在不连续的问题。矩形板的振动模态信息能够通过求解一个标准的矩阵特征值而得到。最后进行数值计算并与现有的文献结果进行比较，验证了该方法的快速收敛性和计算精确性。

关键词：正交各向异性板；改进Fourier级数；任意弹性边界条件；解析解

Free vibration characteristics of orthotropic rectangular plates

ZENGJun-cai1,WANGJiu-fa1,YAOWang2,YUTao2(1. No. 710 R&D Institute, CSIC, Yichang 433003, China;2. TCM China Tool Consulting & Management Ltd. Shanghai 200137, China)

Abstract:An improved Fourier series method was proposed to develop the transverse vibration model of orthotropic rectangular plates and derive the matrix equation which is equivalent to governing differential equations. An analytical solution for vibration of plates with general elastic boundary conditions was provided. The vibration displacement was solved as the linear combination of a double Fourier cosine series and an auxiliary series. The use of these supplementary series is to solve the discontinuity problem encountered in the partial differentials of displacement function along the edges. The vibration mode characteristics were obtained by solving the eigen values of the matrix. Several numerical examples were given and the comparison of the results with those of the available literature validates the convergence and correctness of the method.

Key words:orthotropic plates; improved Fourier series; general elastic boundary support; analytic solution

基金项目：国家自然科学基金(51075215,51475246);江苏省自然科学基金(BK20131402)

中图分类号:TP533

文献标志码：A DOI:10.13465/j.cnki.jvs.2015.24.021

收稿日期：2014-10-13修改稿收到日期：2014-12-12