基于位移正反馈的力与位移切换控制加载方法

谭晓晶， 王　贞， 吴　斌， 周惠蒙， 阿拉塔

(1.云南省建筑科学研究院，昆明　650223； 2.哈尔滨工业大学，哈尔滨　150090；3.中国地震局工程力学研究所，哈尔滨　150080； 4.云南省地震工程勘察院，昆明　650041)



基于位移正反馈的力与位移切换控制加载方法

谭晓晶1， 王贞2， 吴斌2， 周惠蒙3， 阿拉塔4

(1.云南省建筑科学研究院，昆明650223； 2.哈尔滨工业大学，哈尔滨150090；3.中国地震局工程力学研究所，哈尔滨150080； 4.云南省地震工程勘察院，昆明650041)

拟动力试验技术是检验结构抗震性能的一个重要手段[1-4]。然而在进行拟动力试验时，电液伺服作动器只能采用力控制或位移控制中的一种模式工作，无法实现力与位移之间的自动实时切换。通常当试件的刚度很大时采用力控制加载模式，而当其刚度衰减时则采用位移控制加载模式，这样能充分利用两种不同加载控制模式的优点，提高试验加载的控制精度，使得试验结果更可靠。

对于力与位移切换控制，因为作动器力控制环与位移控制环的控制增益是不同的，那么相应控制电路中的工作电压通常是不一样的。如果在两种控制环之间直接切换，切换瞬间容易导致电路中的工作电流发生突变，进而引起电液伺服作动器发生瞬间的突发性运动。这种突发性运动不仅严重影响作动器控制的平稳性和试件的安全性，还导致试验误差产生(见图1)。因此，如何实现力与位移控制之间的平滑切换是该类试验方法的关键问题。

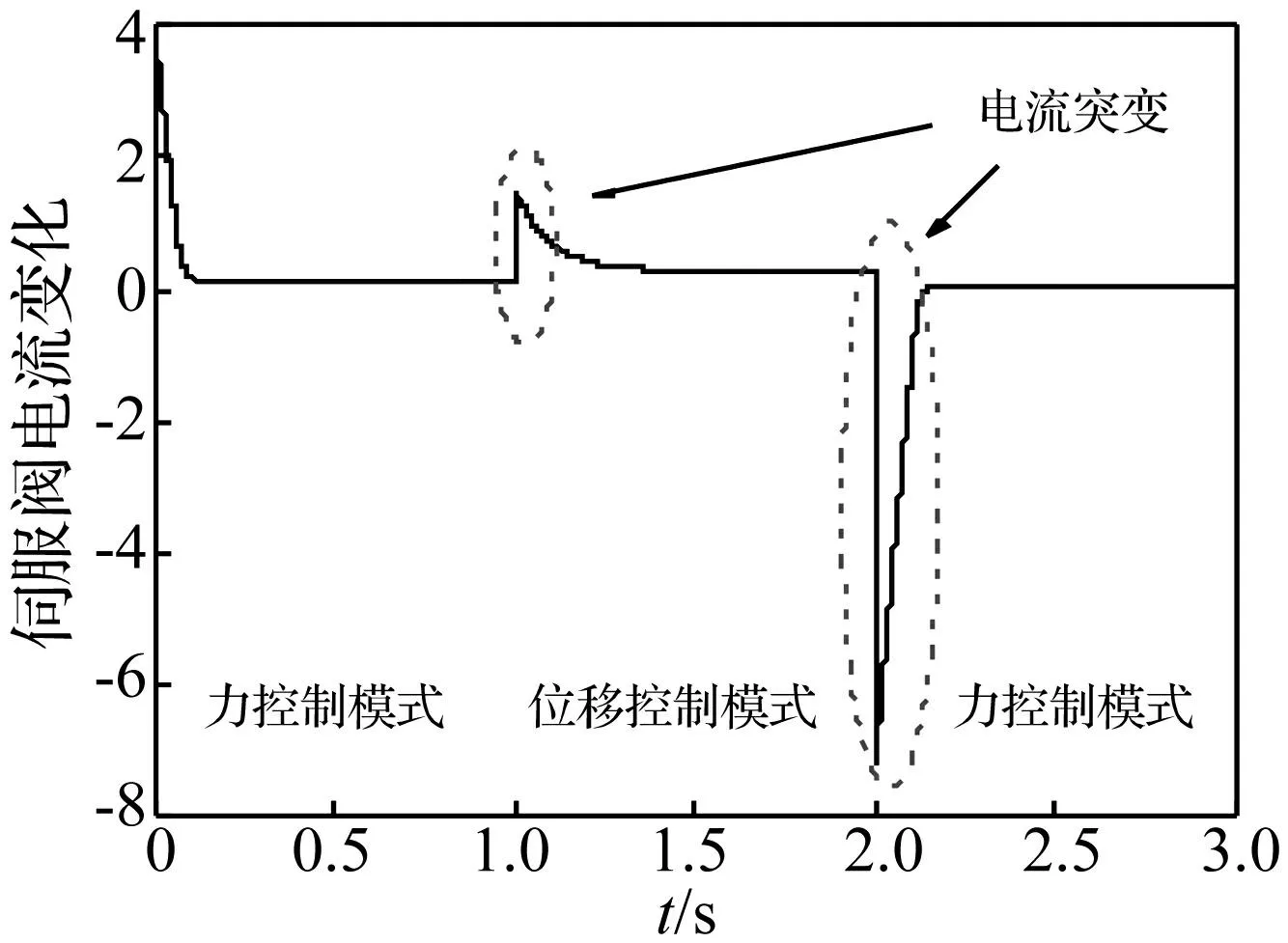
图1　作动器伺服阀电流在切换瞬间的突变Fig.1 Sharp increments of servo-valve current of the actuator at switching instant

对于力与位移切换控制研究，唐志贵[5]提出了“二阶误差为零”的方法来确保试验机在各种状态下的平稳切换。但是该方法过于复杂，需要设计专门的二阶误差信号运算及切换控制逻辑模拟电路，在切换过程中还需要手动操作，自动化程度低，切换不够平稳且有一定的冲击性，得到的实际切换效果并不理想。此外该方法并未考虑力与位移控制环的控制增益不相同的情况。文献[6]阐述了MTS公司电液伺服材料试验机的自动切换功能。相比较前一种方法，该系统采用了计算机程序来控制状态切换，自动化程度提高，但是对于数字电路部分需要编制复杂的控制程序，通用性不强，并且该系统也未考虑力与位移控制环的控制增益不相同的情况。黄勇等[7]提出了数字PID控制器和模型跟踪自适应控制器的平滑切换算法。对于数字PID平滑切换算法，采用修改切换后的输入命令以使得切换前后闭环控制误差相等的办法来完成状态切换，然后再调整控制器参数以进行新状态的控制。但是控制参数的再次调整又会影响之前的切换控制效果，同时对于连续多次状态切换该方法又过于繁琐，因为每次切换均需要修改切换后的输入命令，并更改相应的控制器参数。周烁等[8]针对振动主频大范围快速变化、且伴有大量宽频干扰的复杂机械振动现象，采用多个二阶滤波器代替系统模型，改进了传统的多模型切换控制方法，实现系统的主动隔振。这种方法避免了对整体系统的建模和辨识，减轻了计算量，解决了切换控制过频和不收敛的问题。但该方法仅用于系统不同控制算法之间的切换，难以应用到电液伺服作动器的力与位移切换控制中。对于力和位置的精确控制，盖盛焘等[9]提出了内模控制加前馈补偿的二自由度位置控制器和带位置内环的力控制器，成功实现了机器人末端执行器的精确定位和接触力控制。但是该方法实现的是力与位置混合控制，并不是切换控制。高炳微等[10]通过分别建立位置控制系统和力控制系统，采用基于修正因子的模糊切换控制方法，实现了电液伺服系统位置控制和力控制之间的平滑过渡。该方法的修正因子和切换控制的实现均依赖于反馈力的有和无，而拟动力试验加载过程中反馈力始终存在，该方法难以实施。岳永恒[11]对磁流变阻尼器汽车悬架系统的切换控制进行了研究，但该切换控制仅在整个控制系统中不同控制器之间实施，尚无法应用到电液伺服加载系统中。

针对上述问题，本文提出了一种基于位移正反馈的力与位移切换控制方法，该方法不需要试验系统在硬件上有任何变动，且电液伺服作动器可以保持出厂时的设置。在切换过程中，作动器始终采用位移控制模式工作，即在位移控制模式下实现力的反馈控制。

1基于位移正反馈的力与位移切换控制原理

本文所提出的切换算法的目标是平稳、快速切换，后者是该方法的另一特色。一般而言，伺服控制系统的控制类别和控制参数确定后，其运动轨迹主要取决于两个因素，即命令和控制器状态。因此，理想的切换算法需要同时处理切换前后命令变化和控制器状态间断带来的问题。对于前者，可以适当选择切换瞬间的命令，再与切换后的命令进行内插，就能保证命令的连续。对于后者，需要设定切换瞬间控制器的初始状态。较简单的处理方法是设定为零，即与试验的第一步类似，这么做的缺点是在某些情况下不能保证运动的快速性。比如切换后的控制模式采用PI控制器，需要适当选择积分项的初值，否则若从零开始重新累积控制误差，可能导致切换后作动器运动较慢甚至方向不正确。显然，对于切换前处于稳定状态的系统，理想的切换算法必须保证切换后系统仍然处于稳定状态，否则就可能带来不必要的波动。根据这个认识，就可以确定命令初值和控制器状态初值。

类似地，力与位移切换控制也可以在现有的力反馈环外附加一个力的正反馈和位移负反馈来实现，该思路也仅是本文方法的一种变换而已。

下面以位移环和力环均采用PI控制器的情况为例来讨论该方法的更多细节问题，图2中

(1)

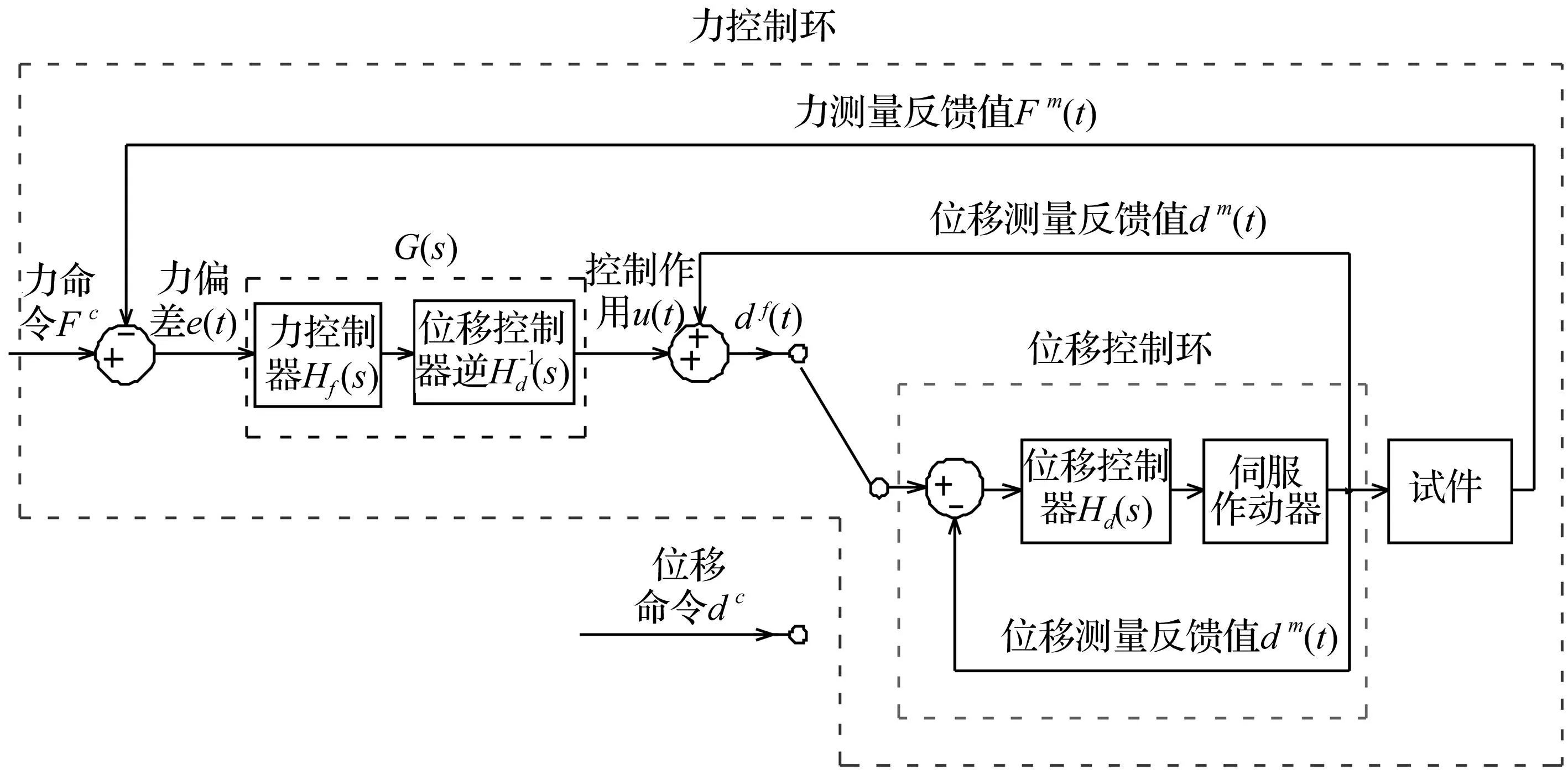
图2　基于位移正反馈的切换控制试验方法原理图Fig.2 Schematic diagram of switching control method based on positive displacement feedback

(2)

(3)

式(3)可在时域中表示为

(4)

式中：e(t)=Fc(t)-Fm(t),u(t)=df(t)-dm(t)。

(5)

式中：δt为试验的采样周期。由式(5)可得

(6)

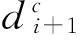
(7)

(8)

式中：Δt为试验的单步加载时间步长，j为单步命令的插值序数，t为试验加载时间。但是一般而言，若在该切换之后不进行位移命令内插，仅会带来较小命令跳跃，与位移阶跃命令类似，可以不做处理，本文的后续数值模拟分析将涉及该问题。显然，该切换过程一定满足前述理想切换算法的基本要求，即切换前处于稳定状态的系统，切换后系统仍然处于稳定状态。实际上从力控制模式切换为位移控制模式时，对于作动器控制而言仅仅是输入的位移命令发生了变化，这与标准的位移控制方式是一样的。

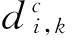
(9)

由式(5)可以得到

(10)

(11)

则

(12)

(13)

(14)

式(12)表明，切换瞬间并不需要保证位移响应与位移命令相同，可容许存在一定的位移控制误差，也就是说该方法能应用到控制过程的动态切换。另一方面，该式表明若位移控制误差为零或者很小，力命令的初值即为当前实测反力(后续模拟中采用了该结论)。在该分析中，已经采用了

(15)

即已经完成了控制器状态的更新。

该分析表明，根据理想切换的基本要求和合理假定，能推导得到切换后命令初值和控制器状态初值。在此基础上，就能保证命令和控制器状态的平滑性，进而能够实现平稳、快速切换。切换控制方法的流程图如图3所示。

图3　切换控制方法的流程图Fig.3 The flow chart of the proposed switching control method

2数值模拟分析

切换控制方法的关键在于保证切换的平稳性。为了验证该切换控制方法的平稳性，本节采用持荷加载方式来进行切换控制试验加载的数值模拟。数值模拟采用Simulink仿真软件，系统的采样频率为1 000 Hz；试验对象为线弹性模型，刚度KE= 13 kN/mm；设计的力控制器参数为KP= 0.002 5，KI= 0.003 5 /s，位移控制器参数为KP= 1.0，KI= 1.418 /s；模拟的作动器力与位移量程分别为±630 kN和±250 mm，力与位移噪声的幅值均取为相应量程的千分之一。模拟过程中先采用位移控制模式加载，位移命令为1 mm；然后切换为力控制模式，力命令为13 kN；最后再切换为位移控制模式，位移命令为1 mm。每步持荷时间均为1 s。得到的模拟结果如图4所示。

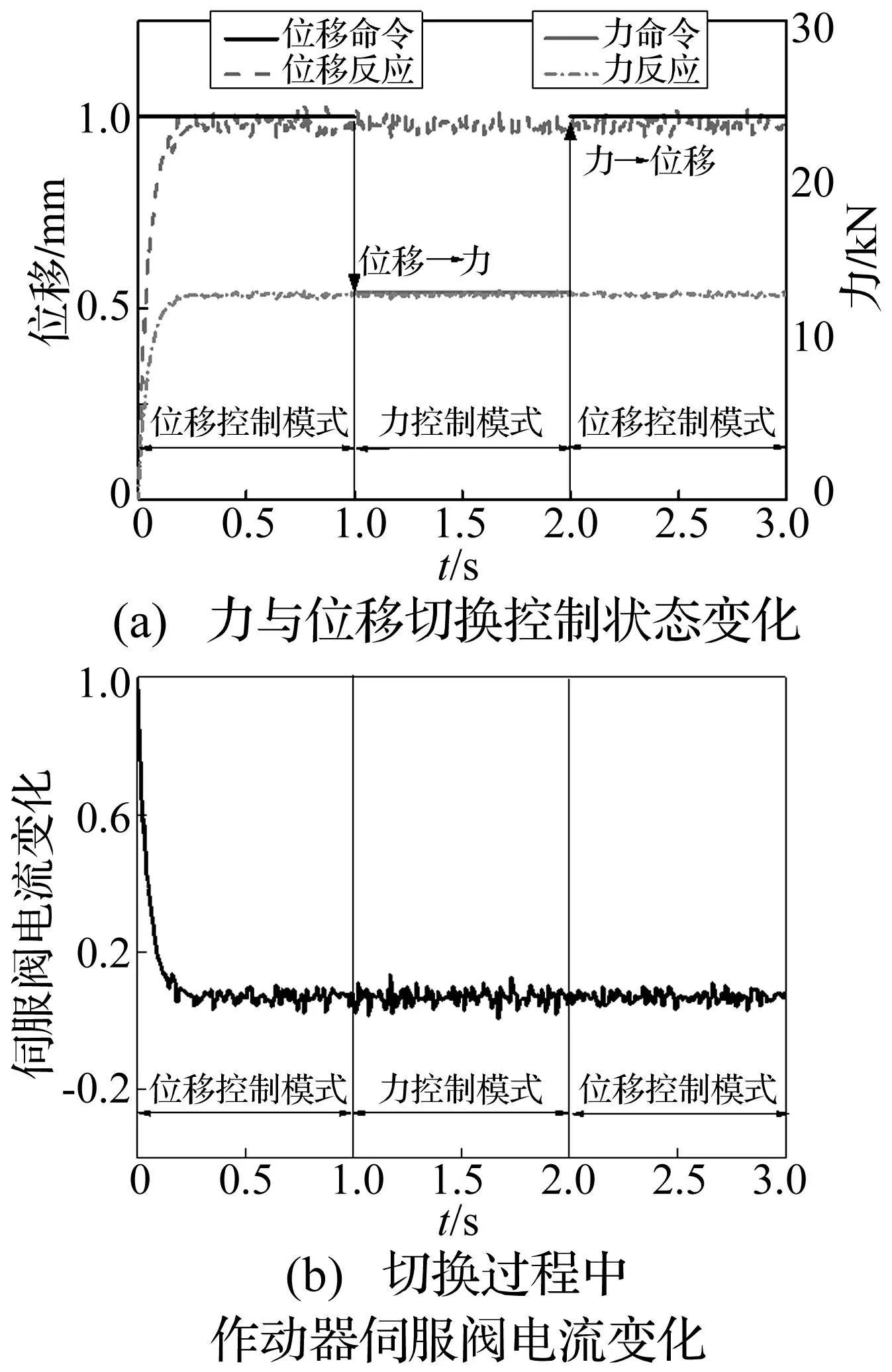
图4　切换控制方法的平稳性验证Fig.4 Stationarity verification of the switching control method

从图4(a)中可以看出，两个控制模式中的反应均能很好地跟踪相应的加载命令，说明设计的控制器能起到很好的控制作用。从结果分析来看，位移控制存在约3%的稳态误差，而力控制存在约1%的稳态误差，均满足试验控制精度要求。在力与位移切换的瞬时，作动器的响应保持稳定状态，无冲击现象发生。并且作动器伺服阀的工作电流也未产生突变，图4(b)所示。可以看出，模拟过程中力与位移控制模式之间能很好地衔接起来，该切换控制方法是可行的，能实现平稳切换。

3切换控制试验验证

为了验证力与位移切换控制加载方法，设计制作了一个足尺钢结构立柱作为试验加载对象。立柱的顶部用螺栓连接了一个水平加载H型钢横梁，底部锚固在试验台座上，试验加载装置如图5所示。

本次试验在哈尔滨工业大学力学与结构试验中心完成。试验的加载设备采用MTS公司的电液伺服作动器，其力与位移量程分别为±1 000 kN和±500 mm。试验系统的控制采用Flex Test GT控制器与MTS液压控制系统的MTS793.10软件来完成。通过MTS793.10软件中的计算编辑器完成力控制环与位移控制环相应程序的编写，设定相应的力与位移命令，并通过其中的多目标试验模块(MPT)控制试验指令的发送及试验加载的进行。

图5　钢结构立柱力与位移切换控制的试验加载装置Fig.5 Setup for the force-displacement switching control test of the steel column

通常拟动力试验的命令多采用阶跃形式发送，因此该试验用以验证多步阶跃形式命令下的力与位移切换控制的可行性。试验设定了力与位移命令的交替发送，且每步命令加载持续时间为10 s，共进行4步加载。根据该试件设计试验控制系统的位移控制器PI参数分别为KP= 1.3、KI= 0.1 /s，力控制器PI参数分别为KP= 0.04、KI= 0.003 /s。

钢柱在力与位移切换控制下得到的试验结果如图6所示。从图中可以看出，控制系统在力与位移控制模式下均能达到很好的控制效果，作动器每一步的力和位移响应均能很好地跟踪其命令。从试验加载控制精度来分析，两种控制模式达到稳态时，位移控制的稳态误差约为1%，而力控制的稳态误差约为2%，均满足试验加载精度要求，同时也说明位移控制器参数取值要优于力控制器参数，该力控制器参数并不是最佳值。在力与位移切换的瞬间，力控制与位移控制之间能很好地衔接，作动器无冲击现象发生。说明在切换前后作动器能实现平稳的、连贯的加载。由此可以看出，该切换控制方法是可行性的，可以成功地实现力与位移之间自动而又平稳的切换。

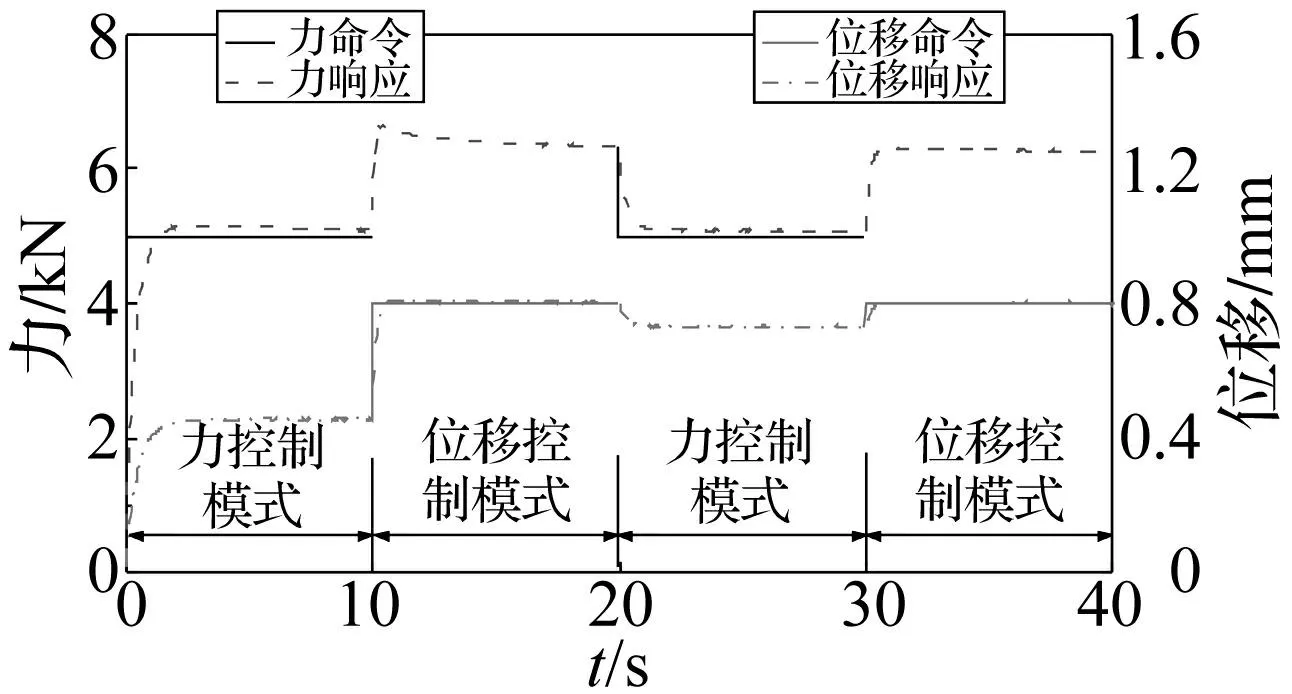
图6　力与位移切换控制试验结果Fig.6 Results obtained in force-displacement switching control test

4结论

提出了基于位移正反馈的力与位移切换控制试验方法，以PI控制为例深入阐述了该方法的实现原理，主要结论如下：

(1) 位移正反馈环能消除加载控制系统封装的位移控制回路，是该平稳切换控制方法的基础。通过该正反馈环，能在不改动试验硬件设备的情况下实现力与位移的自动切换。

(2) 持荷加载数值模拟表明该方法能很好地实现力与位移之间的平稳切换。

(3) 钢柱的力与位移切换控制试验进一步验证了该方法的可行性和有效性。

参 考 文 献

[1] Mahin S A, Shing P B. Pseudodynamic method for seismic testing [J]. Journal of Structural Engineering, 1985,111(7):148-1503.

[2] Aktan H M. Pseudo-dynamic testing of structures[J]. Journal of Engineering Mechanics, 1986,112(2):183-197.

[3] Takanashi K, Nakashima M. Japanese activities on on-line testing [J]. Journal of Engineering Mechanics, 1987,113(7):1014-1032.

[4] Shing P B, Nakashima M, Bursi O S. Application of pseudodynamic test method to structural research [J]. Earthquake Spectra, 1996,12(1):29-56.

[5] 唐志贵. 电液伺服疲劳试验过程中控制方式的转换[J]. 试验机与材料试验, 1985, (1): 50-52.

TANG Zhi-gui. Switching control mode of the electro-hydraulic servo during fatigue tests[J]. Test Machine and Material Test, 1985(1):50-52.

[6] 陈申, 何肖瑜. 材料试验机控制状态的自动切换[J]. 试验机与材料试验, 1986 (3): 24-28.

CHEN Shen, HE Xiao-yu. Automatic switchingof the control state of material testing machine[J]. Test Machine and Material Test, 1986(3):24-28.

[7] 黄勇, 崇生, 史维祥. 电液伺服试验机中负刚度问题的研究[J]. 机床与液压, 1999, (1): 9-11.

HUANG Yong, CHONG Sheng, SHI Wei-xiang.Study on negative stiffness problem ofthe electro-hydraulic servo testing machine[J]. Machine Tool & Hydraulics, 1999(1):9-11.

[8] 周烁，李运堂，孟光，等. 基于干扰观测的切换控制方法在主动隔振中的应用研究[J]. 振动与冲击，2006，25(6)：121-123.

ZHOU Shou, LI Yun-tang, MENG Guang, et al. Active vibration isolation with switching control method based on disturbance obaservation[J]. Journal of Vibration and Shock, 2006, 25(6): 121-123.

[9] 盖盛焘，朱晓蕊. 力-位移控制算法在工业系统中的应用[J]. 微计算机信息，2009, 23(8): 173-175.

GAI Sheng-tao, ZHU Xiao-rui. Industrial application of position-force control[J].Microcomputer Information, 2009, 23(8): 173-175.

[10] 高炳微，邵俊鹏，韩桂华. 电液伺服系统位置和力模糊切换控制方法[J]. 电机与控制学报，2014,18(5)：99-104.

GAO Bing-wei, SHAO Jun-peng, HAN Gui-hua. Fuzzy switching control between position and force for electro-hydraulic servo system[J]. Electric Machine and Control, 2014, 18(5): 99-104.

[11] 岳永恒. 基于磁流变阻尼器的汽车悬架系统切换控制[D]. 哈尔滨：哈尔滨工业大学，2013.

第一作者 谭晓晶 男，博士，高级工程师,1979年10月生

摘要：为了结合力控制与位移控制两种不同试验加载控制模式的优点，并在拟动力试验中实现两种模式的自动切换，提出了基于位移正反馈的力与位移切换控制方法。首先从理论角度分析了切换控制过程，然后从数值模拟和试验角度分别验证了该方法的可行性和有效性。研究结果表明，该方法能很好地实现力与位移控制模式之间自动而平滑的切换。

关键词：位移正反馈；位移控制；力控制；切换控制

Switching control method between force control mode and displacement control mode based on positive displacement feedback

TANXiao-jing1,WANGZhen2,WUBin2,ZHOUHui-meng3,Alata4(1. Yunnan Institute of Building Research, Kunming 650223, China; 2. Harbin Institute of Technology, Harbin 150090, China; 3. Institute of Engineering Mechanics, China Earthquake Administration, Harbin150080, China; 4. Yunnan Institute of Earthquake Engineering Investigation, Kunming 650041, China)

Abstract:A force-displacement switching control method based on a positive displacement feedback loop was proposed in order to combine the advantages of the force control mode and the displacement control mode and to accomplish automatic switching in pseudo-dynamic testing. The switching process was theoretically analyzed. The numerical simulations and test results demonstrate that the method can provide automatic and smooth switching between force control and displacement control.

Key words:positive displacement feedback; displacement control; force control; switch control

中图分类号:TU317

文献标志码：A DOI:10.13465/j.cnki.jvs.2015.24.012

通信作者吴斌 男，博士，教授，1970年1月生

收稿日期：2015-01-15修改稿收到日期：2015-05-11

基金项目：国家自然科学基金项目资助(51161120360,51110106,51408565);中央高校基本科研业务费专项资金(HIT.ICRST.2010016,HIT.BRET2.2010009);基本业务地震行业科研专项经费项目(2014B13);国家博士后基金面上资助(2014M551293)