叶片旋转噪声激励下旋涡风机壳体声辐射计算理论及分析

左曙光， 何慧娟， 吴旭东， 张琛璘， 韦开君， 王　哲

(同济大学 新能源汽车工程中心，上海　201804)



叶片旋转噪声激励下旋涡风机壳体声辐射计算理论及分析

左曙光， 何慧娟， 吴旭东， 张琛璘， 韦开君， 王哲

(同济大学 新能源汽车工程中心，上海201804)

随着旋涡风机的广泛应用[1-2]，除了性能之外，其噪声也得到越来越多的关注[3-4]。旋涡风机噪声可分为叶片噪声、电磁噪声、流体噪声和机械噪声。无论是哪一种噪声，最终都以力或声载荷的形式激励壳体，引起壳体振动从而向外辐射噪声。因此研究旋涡风机壳体声辐射特性对风机噪声的研究具有重要意义。目前旋涡风机壳体声辐射的公开文献相对较少，而且由于风机壳体结构的复杂性，风机壳体声辐射的计算多采用商业软件数值仿真的方法。Lee等[5]从非定常流场中利用声类比提取出的声源信息并结合BEM软件sysnoise计算了叶片噪声激励下离心风机壳体的声辐射。左曙光等[6]采用边界元软件virtual lab模拟了旋涡风机壳体在流体噪声激励下的远场辐射噪声，并探讨了壳体散热片以及结构阻尼对壳体声辐射的影响。尽管商业软件数值计算结果较精确，但需耗费大量时间，使得对风机结构参数的影响因素分析有限，从而无法快速实现进一步的结构优化。而采用理论计算方法，通过对风机壳体进行合理简化，实现对壳体声辐射的快速预测，有助于叶片结构参数对壳体声辐射的影响因素分析。

本文根据旋涡风机内螺旋形流动及风机叶片和流道的尺寸确定尾流面，对叶片表面及尾流面离散化，并基于面元法求解叶片表面气动载荷。根据Farassat改进的FW-H声波方程得到叶片旋转噪声，并利用Fluegge薄壳理论和拉格朗日能量法建立旋涡风机壳体动力学模型。基于Helmholtz边界元法，建立风机壳体远场辐射声压的理论计算模型。通过试验验证了该理论模型的有效性，并通过与商业软件仿真的对比验证了该模型的时效性。最后根据理论计算模型分析叶片结构参数对叶片旋转噪声激励下壳体声辐射的影响。

1叶片噪声激励下风机壳体声辐射计算方法

1.1叶片表面气动载荷计算

旋涡风机运转会引起内部流体非定常运动，旋转叶片表面受到非定常力而形成随时间变化的压力脉动。叶片表面的压力脉动即气动载荷的变化是叶片噪声产生的根本所在。借鉴航空航天领域中有关螺旋桨噪声的计算思路，先确定叶片表面的气动载荷。相比于速度面元法，速度势面元法计算量和存储空间小，轴流风机等旋转机械的气动载荷计算均基于速度势面元法。根据速度势面元法，格林公式导出的物面积分方程为：

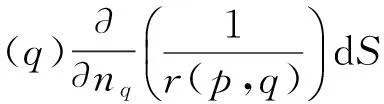
(1)

式中：Δφ为尾流面上速度势差。积分方程中三项积分分别为在物体表面上强度为φ(q)的偶极子分布，物体表面强度为Vref·nq的源分布和尾流面上强度为Δφ(q)的偶极子分布。

根据面元法数值计算方法[7]，需将旋涡风机叶片和尾流面进行离散。对叶片进行均匀厚度、忽略倒角和圆角的简化后，沿叶片展向和弦向对每个叶片的压力面和吸力面进行面元划分。由于简化后的叶片表面均为平面，采用平面四边形面元来表示叶片表面。为减小数值计算结果偏差，在叶根和叶尖处取较密的面元。

由于绕风机轴线的周向运动和叶片间的循环流动的结合，旋涡风机的流动形式为特有的螺旋形流动[2]。借鉴航空航天领域飞机螺旋桨的经验尾流面模型方法，将其应用到旋涡风机尾流面的建模。假设尾流面的形状与旋涡风机流动形式相一致，在其基础上建立尾流面的几何形状。采用I S Yoo等人的求解循环流动中心方法[8]，如图1。

图1　旋涡风机循环流动中心示意图Fig.1 Circulating flow center of regenerative blower

根据叶轮和流道几何参数，可确定循环中心：

(2)

式中：b为叶片宽度，d为流道深度，t为叶片厚度，Z为叶片数目，r2为叶轮半径，Bu和Bb分别为以循环流动中心为界的上下部分的体积流量。

结合叶片宽度与流道宽度的几何尺寸，叶片内循环流动半径与流道内的循环流动半径为：

(3)

(4)

式中：r0为轮毂半径。

确定了叶片间循环流动相关参数后，并结合叶片的周向流动，可得到尾流面的几何模型，如图2。

图2　尾流面模型图(单位：m)Fig.2 Model of wake flow surface

根据叶片及尾流面离散结果，对边界积分方程(4)进行离散，在叶片的四边形面元上布置相等强度的源汇和偶极子，在尾流面上仅布置相等强度的偶极子，则离散的边界方程为：

(5)

式中：δij表示Kronecker数，即当i=j时，δij=1；当i≠j时，δij=0。N为旋涡风机所有叶片的面元数，Cij，Bij和Wij分别表示各叶片面元上偶极子强度的影响系数、叶片面元上各源汇间的影响系数以及尾流面的偶极子对叶片面元上偶极子的作用。

考虑到尾流面上的偶极子强度按照压力库塔条件是由物面尾缘处上下表面的速度势之差而形成，即Δφ=φ+-φ-，则方程(5)可简化：

(6)

当叶片上的面元位于尾缘处时，Aij=Cij±Wij，而当面元在非尾缘处时，Aij=Cij。将式(6)展开得：

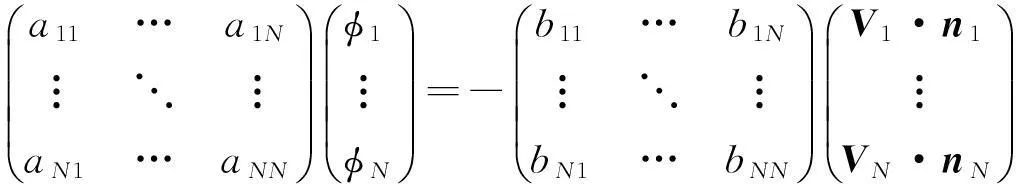
等式两边同时乘以影响系数矩阵的逆阵，可求得叶片表面每个面元上的速度势值。再对计算得到的速度势值求导，求得面元上扰动速度值。最后利用伯努利方程即可求得叶片表面气动载荷值。

1.2叶片旋转噪声计算

旋涡风机的叶片旋转所产生的离散噪声对风机的总体噪声起着主要贡献和影响，同时也是引起壳体声辐射的主要激励源[9]。由气动声学理论可知，对于旋涡风机这种亚声速工况下的旋转机械，其叶片离散噪声由与叶片表面非定常力有关的偶极子声源和与叶片表面速度有关的单极子声源所构成[10]。

本文中旋涡风机叶片旋转噪声的计算采用Farassat改进的FW-H方程的噪声时域计算方法[11]：

p=pT+pL

(8)

式中:p为声压，等式右边分别代表单极子声源和偶极子声源引起的噪声。当叶片表面气动载荷、叶片结构参数及风机转速已知时，即可求得叶片噪声时域解，具体计算表达式见文献[11]。

在离风机中心1米处按轴向和周向布置声压测点。设风机中心在固定坐标系中为原点O(0,0,0)，远场各声压测点为:轴向：X1(1,0,0)、X2(-1,0,0)；周向：X3(0,1,0)、X4(0,-1,0)、X5(0,0,-1)。具体位置如图3所示。

图3　远场声压测点位置图Fig.3 Point location measuring sound pressure in far field

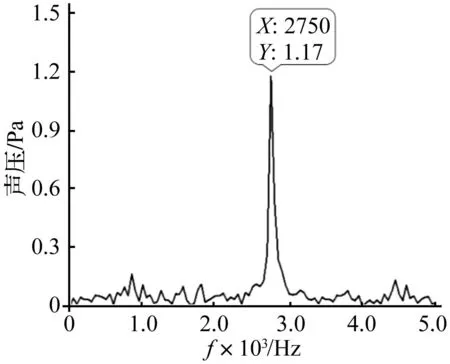
图4　监测点X5的声压频域图Fig.4 Amplitude frequency diagram of sound pressure at X5

对各声压测点所得时域信号进行傅里叶变换得到频域信号。5个测点的频域信号类似，明显峰值均在叶片通过频率处(2 750 Hz)，周向测点X5的频域图如图4所示。各测点叶片通过频率(BPF)处的声压幅值如表1。

表1　测点叶片通过频率处的声压幅值

从五个远场测点的声压幅值上可看出，在离风机中心相同距离的情况下，风机周向的声压值明显大于轴向声压值。

1.3旋涡风机壳体动力学模型

对旋涡风机来说，叶片噪声主要是通过作用在风机的壳体上使之产生振动，最终以声辐射的形式传播到远场监测点。根据上述旋涡风机叶片旋转噪声的指向性，即周向的声压值明显大于轴向的声压值，在不考虑与结构共振的前提下，风机壳体周向上的振动要大于风机轴向上的振动。另外在对两端封闭的风机壳体进行模态分析数值仿真时发现，在低于2 000 Hz的低频段，模态主要体现为壳体轴向的振动，在高于2 000 Hz的高频段内，绝大多数的模态振型主要体现为壳体径向的振动[12]。而作为声激励的风机叶片旋转噪声刚好位于2 000 Hz以上的高频段内，因此旋涡风机壳体周向的振动特性是本文关注的重点。根据噪声激励和壳体模态的结论对风机壳体进一步简化，忽略壳体两端端盖的影响。

旋涡风机壳体简化模型及坐标系如图5所示，为一有限长圆柱壳体结构。图中，圆柱壳的壳体中面半径为R，壳体厚度为h，壳体长度为L；坐标系中的x轴方向和θ方向分别为圆柱壳体的轴向和周向方向，并以壳体一端圆的中心点作为坐标轴原点O；u,v,w分别代表壳体表面微元的轴向、周向和径向位移。

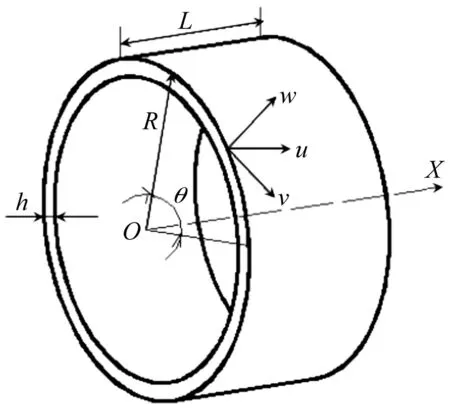
图5　旋涡风机壳体简化模型Fig.5 Simplified model of regenerative blower’s shell

由于风机壳体厚度远小于壳体直径，基于Fluegge薄壳理论[13]的假设，并利用能量法，建立风机壳体动力学模型如下[14-15]：

圆柱壳体的动能表达式为：

(9)

式中：ρ为壳体的密度；dz为壳体微元的厚度。

圆柱壳体的势能表达式为：

(10)

式中：E为壳体的杨氏弹性模量，υ为泊松比。

得到动能与势能的表达式之后，就可利用拉格朗日法进行求解。拉格朗日能量法为：

(11)

式中:F为叶片旋转噪声激励力，q为壳体振动位移，n表示周向。

针对声激励的计算，首先将圆柱壳体沿轴向和周向划分得到面元，计算各面元中心控制点(面元形心)处的声压。然后计算各面元的面积，并结合已获得的声压大小，得到各面元的声激励大小。声激励的方向均为圆柱壳体径向方向。

采用Ritz方法来描述壳体的周向和轴向位移分布，并设力的作用点为(x,R,θ)，则作用于风机壳体的径向激励为：

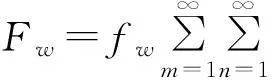
(12)

式中:fw为激励的幅值大小，即为声压p与面元大小的乘积；ω′表示激振频率。

将声激励下圆柱壳体的振动计算转化为多个面激励下圆柱壳体受迫振动的线性叠加。因此，圆柱壳体受迫振动动力学方程为：

(13)

对式(13)整理后，计算圆柱壳体的振动响应，得到振动位移信号和速度信号，表达式为：

(14)

(15)

1.4风机壳体声辐射理论计算模型

求解声辐射问题就是求解波动方程在特定边界条件下的解。利用圆柱壳体受迫振动计算所得结果，结合Helmholtz积分方程，并对壳体表面进行离散化，从而得到任意边界下远场某点声压理论计算表达式[16]。

C(X)p(X)=

(16)

式中:p为声压；ω为振动频率，c为声速，ρ为流体密度，vn为结构体法向振速，即式(15)的叶片噪声激励下圆柱壳体的振动速度信号。C为场点的位置系数，一个仅与边界几何形状有关的量。当场点位于声辐射物体外任意一空间位置时，C=1；当场点位于光滑的声辐射物体表面时，C=0.5。G为自由空间格林函数[17]：

(17)

将式(17)进行离散化处理，考虑计算精度及时间成本，本文采用四节点四边形线性等参单元模拟壳体表面，各节点形函数为[18]：

(18)

式中：ζ和η为各单元局部坐标系中的坐标轴，用来表示等参单元的形函数。

在确定形函数之后，则原各单元上速度和压力可表示为四个节点上速度和压力的线性叠加：

(19)

(20)

将上式代入离散化后的Helmholtz边界积分方程中，并令：

(21)

(22)

则离散化后的边界积分方程为：

(23)

利用上式可计算壳体远场声辐射，计算步骤为：将已知量物体表面法向振速(15)代入式(23)中，先计算得到物体表面声压(C=0.5)，之后再次利用式(23)，获得除物体表面外空间上任一点的声压大小(C=1)。

2理论计算模型有效性及时效性的验证

2.1理论计算模型有效性验证

风机叶片结构参数和壳体结构参数如下。

根据GBT2888-91《风机和罗茨鼓风机噪声测量方法》中关于风机壳体噪声的测点布置要求：测点位置在通风机主轴水平面内、经过叶轮几何中心的直线上，距离壳体1 m处。测点为C1、C2、C3、M1、M2、M3；在其基础上再增加两个测点，分别位于C1和M3中间的C5及C3和M1之间的C4，这两点都距离风机壳体1 m，如图6。

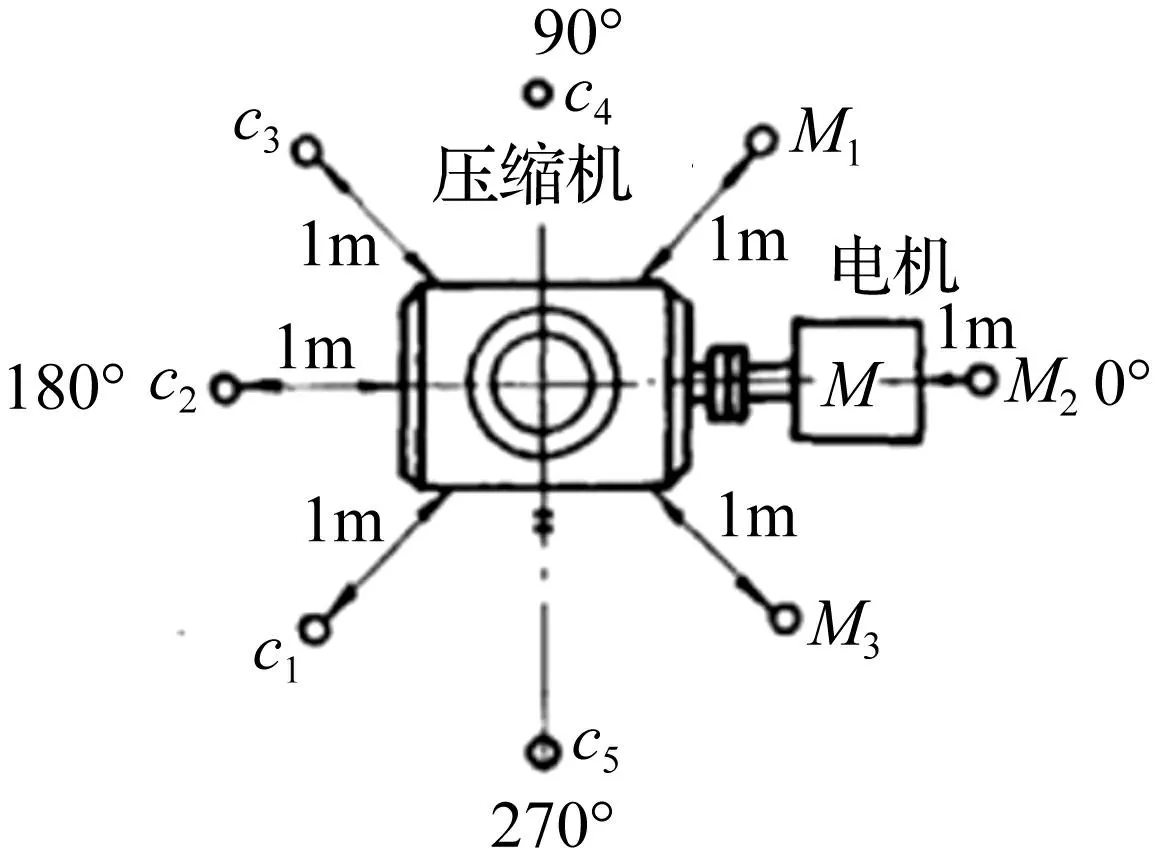
图6　风机壳体噪声的测点分布图Fig.6 Point distribution of measuring the fan shell noise

8个测点的试验噪声值与基于壳体声辐射理论计算模型的相同位置测点下的理论计算值对比如图7。

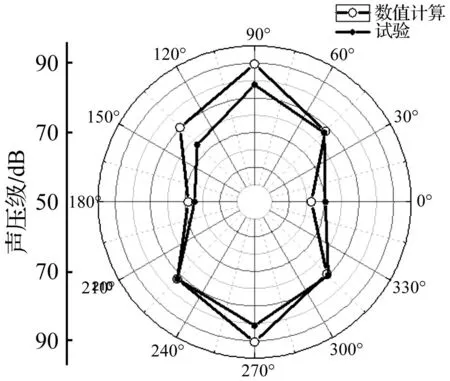
图7　理论计算结果与试验结果圆周分布图Fig.7 Circular distribution of theoretical calculation and test

从图7可得，理论结果中风机周向上测点的声压值明显大于其它位置的声压值，与试验结果一致，表明风机主要的辐射噪声源是在风机周向的位置。

由于理论计算未考虑壳体对声波的反射、透射而导致的能量损失，大多测点的理论计算结果略大于试验结果；由于理论计算未考虑与进出口相连接的进出口管道的声辐射噪声，靠近进出口位置(0°)处的理论结果略小于试验结果。误差均在可接受范围之内。因此，该壳体声辐射理论计算模型具有有效性。

2.2理论计算模型时效性验证

目前风机叶片旋转噪声及壳体声辐射的计算分析大多基于多个商业软件的联合数值仿真，本文所建立壳体声辐射理论计算模型能实现壳体声辐射的快速计算。采用理论计算模型和商业软件进行叶片噪声激励下壳体声辐射的计算时间对比见表3。

表3　计算时间对照表

由表3可知，与商业软件相比，该理论计算模型大幅减少了计算时间，为叶片结构参数进行影响因素分析及进一步结构优化设计奠定了有利的基础。

3叶片结构参数对壳体声辐射的影响

根据叶片噪声激励下风机壳体声辐射计算方法，不同的叶片结构参数会改变叶片表面气动载荷，从而改变叶片旋转噪声，引起风机壳体声辐射不同。为获得较低的叶片噪声激励下的壳体声辐射噪声，本文对影响叶片噪声激励的叶片主要结构参数如叶片数、叶片弯角、叶片宽度、叶片厚度等进行了影响因素分析，对叶片的结构设计具有指导意义。

3.1叶片数

分析叶片数的改变对壳体远场辐射噪声的影响，叶片数分别取45、50、55、60、65。远场辐射噪声的结果如下。

由图8得出，随着叶片数的增加，平均声压级呈单调递减的趋势。叶片数从45增加到65，声压级从82.4 dB减小到76.0 dB。叶片数小于55时，壳体声辐射声压级随叶片数的变化较快，而叶片数大于55时，声压级随叶片数的变化相对较慢。

3.2叶片厚度

分析叶片厚度的改变对壳体远场辐射噪声的影响，叶片厚度分别取2 mm、3 mm、4 mm、5 mm、6 mm。远场辐射噪声的结果(见图9)。

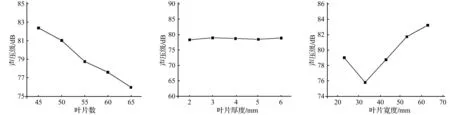
图8 叶片数对壳体声辐射影响Fig.8Effectsofbladenumberonshellsoundradiation图9 叶片厚度对壳体声辐射影响Fig.9Effectsofbladethicknessonshellsoundradiation图10 叶片宽度对壳体声辐射影响Fig.10Effectsofbladewidthonshellsoundradiation

由图9得出，当叶片厚度增加时，壳体声辐射平均声压级有升有降，但其变化的幅值并不明显。从2 mm叶片厚度到6 mm叶片厚度，声压级最大值为79.0 dB，最小值为78.4 dB，仅相差0.6 dB。因此，可以认为叶片厚度对风机壳体声辐射声压级没有影响。

3.3叶片宽度

分析叶片宽度的改变对壳体远场辐射噪声的影响，叶片宽度分别取23 mm、33 mm、43 mm、53 mm、63 mm。远场辐射噪声的结果见图10。

由图10得出，声压级最低点所对应的叶片宽度为33 mm。当叶片宽度从23 mm增加到33 mm，声压级从79.0 dB减小到75.9 dB；叶片宽度从33 mm增加到63 mm，声压级又逐渐从75.9 dB增加到83.2 dB。可知，随着叶片宽度增加，声压级先减小再增大。

3.4叶片弯角

分析叶片弯角的改变对壳体远场辐射噪声的影响，叶片弯角分别取-12°、-8°、-4°、0°、4°、8°、12°。远场辐射噪声的结果见图11。

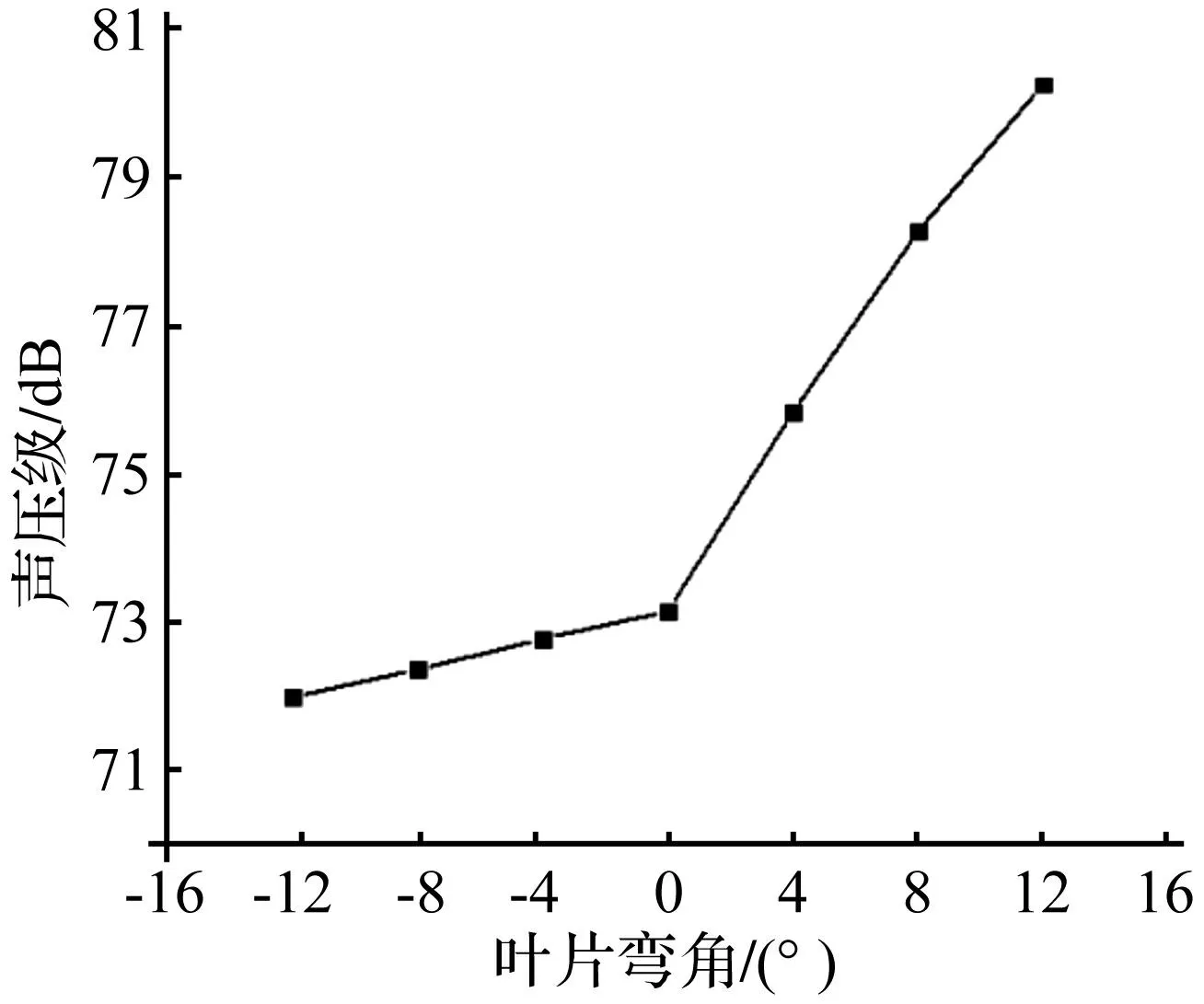
图11　叶片弯角对壳体声辐射影响Fig.11 Effects of blade angle on shell sound radiation

由图11得出，当叶片弯角与旋转方向一致时(即前向叶片，弯角大于0°)，随着叶片弯角的增大，声压级随之增大；而当叶片弯角与旋转方向相反时(即后向叶片，弯角小于0°)，声压级随着叶片弯角的增大而减小。

4结论

(1) 借鉴航空航天领域中螺旋桨桨叶气动载荷求解方法，根据旋涡风机内特有的螺旋流动形式建立尾流面几何模型。对叶片表面与尾流面进行离散化，基于面元法建立了叶片表面非定常气动载荷计算模型。

(2) 基于FW-H声波方程，将叶片表面气动载荷代入叶片噪声时域表达式中，得到叶片旋转噪声。旋涡风机的叶片旋转噪声计算表明，在与旋涡风机中心相同距离下，位于风机周向的声压值要明显大于轴向上的声压值，说明旋涡风机叶片旋转噪声对周向位置起着主要影响。

(3) 对风机壳体结构简化，基于Fluegge薄壳理论和拉格朗日能量法建立了风机壳体动力学模型。将叶片旋转噪声激励作用于风机壳体上，利用边界元理论及Helmholz边界积分方程，得到叶片旋转噪声激励下旋涡风机壳体声辐射。结果表明，风机主要的辐射噪声源位于风机周向位置，与试验结果一致。与商业软件仿真计算相比，理论计算能大幅缩短计算时间，利于叶片结构参数对风机壳体声辐射影响的快速分析。

(4) 以风机壳体声辐射平均声压级作为评价指标，分别对叶片数、叶片厚度、叶片宽度和叶片弯角进行了单因素影响分析，结果表明：叶片数的增加(45~65)使声压级逐渐减小；叶片厚度的改变(2~6 mm)对平均声压级几乎没有影响；随着叶片宽度增加(23~63 mm)，声压级先减小再增大；声压级随前向叶片弯角的增大(0°~12°)而增大，随后向弯角的增加(0°~12°)而减小。

参 考 文 献

[1] Raheel M, Engeda A. Current status, design and performance trends for the regenerative flow compressor and pumps[J]. American Society of Mechanical Engineers, 2002, 7: 99-110.

[2] 韩惠君，左曙光. 叶片参数对旋涡风机性能的影响[J]. 流体机械，2012, 40(7): 15-19.

HAN Hui-jun, ZUO Shu-guang. Effect of blade parameters on performance of regenerative blower[J]. Fluid Machinery, 2012, 40(7): 15-19.

[3] 康强，左曙光，张世炜. 燃料电池轿车用旋涡风机噪声特性分析[J]. 振动与冲击，2011，30(12): 235-240.

KANG Qiang, ZUO Shu-guang, ZHANG Shi-wei. Noise feature analysis foe a vortex blower in fuel cell vehicles[J]. Journal of Vibration and Shock, 2011，30(12): 235-240.

[4] 左曙光，韦开君，宋立廷，等. 燃料电池车用漩涡风机壳体辐射噪声数值预测[J]. 噪声与振动控制，2013,33(3): 142-146.

ZUO Shu-guang, WEI Kai-jun, SONG Li-ting, et al. Numerical prediction of radiation noise for vibrating shell of a regenerative blower in fuel-cell vehicles[J]. Noise and Vibration Control, 2013,33(3): 142-146.

[5] Lee S, Heo S, Cheong C. Prediction and reduction of internal blade-passing frequency noise of the centrifugal fan in a refrigerator[J]. International Journal of Refrigeration, 2010, 33(6): 1129-1141.

[6] 左曙光，宋立廷. 旋涡风机壳体在内流场作用下的动力响应[J]. 振动.测试与诊断，2013(5): 851-855.

ZUO Shu-guang, SONG Li-ting. Dynamic response of the regenerative blower’s shell under the action of the internal flow field[J]. Journal of Vibration，Measurement & Diagnosis, 2013(5): 851-855.

[7] 张永坤，熊鹰. 基于面元法及模型试验的船舶螺旋桨噪声预报方法[J]. 武汉理工大学学报:交通科学与工程版，2008(5): 818-821.

ZHANG Yong-kun, XIONG Ying. Prediction of ship propeller noise using surface panel method and experimental investigations[J]. Journal of Wuhan University of Technology: Transportation Science & Engineering, 2008(5): 818-821.

[8] Yon I S, Park M R, Chung M K. Improved momentum exchange theory for incompressible regenerative turbomachines. Proe. IMechE[J]. Part A: Journal of Power and Energy,2005,219:567-581．

[10] Goldstein M E. Aeroacoustics[J]. New York, McGraw-Hill International Book Co., 1976.

[11] Farassat F, Brentner K S. The acoustic analogy and the prediction of the noise of rotating blades[J]. Theoretical and Computational Fluid Dynamics, 1998, 10(1/2/3/4): 155-170.

[12] 张琛璘. 叶片噪声激励下旋涡风机壳体声辐射计算方法及应用研究[D]. 上海: 同济大学，2014:32-40.

[13] 陈美霞，谢坤，魏建辉. 带框架肋骨圆柱壳体振动特性分析[J]. 华中科技大学学报:自然科学版，2014, 42(3): 127-132.

CHEN Mei-xia, XIE Kun, WEI Jian-hui. Vibration characteristics analysis of cylinder shell with frame rib[J]. Journal of Huazhong University of Science and Technology:Natural Science Edition, 2014,42(3):127-132.

[14] Kwak M K, Heo S, Jeong M. Dynamic modelling and active vibration controller design for a cylindrical shell equipped with piezoelectric sensors and actuators[J]. Journal of Sound and Vibration, 2009, 321(3): 510-524.

[15] Sohn J W, Choi S B, Kim H S. Vibration control of smart hull structure with optimally placed piezoelectric composite actuators[J]. International Journal of Mechanical Sciences, 2011, 53(8): 647-659.

[16] Chapelle D, Bathe K J. The finite element analysis of shells: fundamentals[M]. Berlin: Springer, 2011.

[17] Brebbia C A. Boundary element methods in acoustics[M]. Southampton, Boston: Computational Mechanics Publications, 1991.

[18] Bathe K J. Finite element procedures[M] .laus-Jurgen Bathe, 2006.

第一作者 左曙光 男，教授，博士生导师，1968年6月生

摘要：基于旋涡风机内螺旋形流动，采用面元法和螺旋桨尾流面建模法建立叶片表面气动载荷理论计算模型。根据FW-H方程所得的叶片旋转噪声结果对旋涡风机壳体进行简化，基于Fluegge薄壳理论和拉格朗日能量法建立了旋涡风机壳体动力学模型，并结合边界元法建立了壳体远场声辐射的理论计算模型。理论计算的壳体声辐射指向性表明，壳体声辐射主要是在风机的周向位置，与试验结果一致。且较商业软件仿真，采用该文理论方法的计算时间大幅减少。最后利用理论计算模型，探讨了叶片数、叶片厚度、叶片宽度和叶片弯角对叶片旋转噪声激励下壳体声辐射的影响规律：叶片数的增加使得声压级逐渐减小；叶片厚度的改变对平均声压级几乎没有影响；随着叶片宽度的增加，声压级先减小再增大；声压级随前向叶片弯角的增大而增大，随后向弯角的增加而减小。

关键词：叶片旋转噪声；薄壳理论；壳体声辐射；叶片参数

Sound radiation of regenerative blower’s shell under the rotational noise excitation of blades

ZUOShu-guang,HEHui-juan,WUXu-dong,ZHANGChen-lin,WEIKai-jun,WANGZhe(Clean Energy Automotive Engineering Center, Tongji University, Shanghai 201804, China)

Abstract:Considering the spiral-like flow in regenerative blower, and using the panel method and the modeling method of flow field under propeller, a theoretical model was set up to calculate the aerodynamic load on blade surface. Based on the FW-H equation, the regenerative blower’s shell was simplified. With the thin shell theory and the Lagrange energy method, a dynamic model of regenerative blower’s shell was set up. Using the boundary integral method, a theoretical calculation model of far field sound radiation of the shell was established. The distribution of sound radiation shows that the shell sound radiation is mainly in circumference, which is consistent with the test result. The calculation time consumption is greatly reduced using the theoretical calculation proposed than using the commercial software. According to the model, the influences of blade number, blade thickness, blade width and blade angle on shell sound radiation under the rotational noise excitation were studied. The sound pressure level (SPL) decreases with the increase of blade number. The blade thickness nearly has no effect on the SPL. With the increase of blade width, the SPL decreases at first and then increases. As the blade angle increases, the SPL of forward-curved blade increases and that of backward-curved blade decreases.

Key words:blade rotation noise; thin shell theory; shell sound radiation; blade parameters

中图分类号:TH314

文献标志码：A DOI:10.13465/j.cnki.jvs.2015.24.010

通信作者吴旭东 男，助理教授，博士后，1983年11月生

收稿日期：2014-09-12修改稿收到日期：2014-11-26

基金项目：国家自然科学基金(51305303);国家重大仪器专项(2012YQ150256)