灾害条件下多层次应急疏散模型的构建方法研究*

唐炉亮,杨　雪，刘　章，王雪浩，靳　晨，董　坤

(1 武汉大学 测绘遥感信息工程国家重点实验室，湖北 武汉 430079；2 航天恒星科技有限公司(503所)，北京 100086)



灾害条件下多层次应急疏散模型的构建方法研究*

唐炉亮1,杨雪1，刘章1，王雪浩1，靳晨1，董坤2

(1 武汉大学 测绘遥感信息工程国家重点实验室，湖北 武汉 430079；2 航天恒星科技有限公司(503所)，北京 100086)

摘要:人们每天都要面对各种造成严重财产和人身安全损失的重大灾害，如何建立灾害条件下中国人口高密度大范围的应急疏散模型，具有重大的意义。该文基于我国灾害条件下高密度人口的集体疏散模式，按照灾害区域的具体情况和人口分布，以道路实时速度和路面损毁程度所决定的道路阻抗性作为评判道路疏散能力的依据，构建从危险区域的多集结点到安全区域的多安置点的多层次应急疏散模型，确定集体疏散人员的疏散路径、人数和车辆，实现在最短的时间内的受灾群众整体最优疏散，并以山东省德州发生地震作为实验区，采用GoogleMap API和C#搭建多层次应急疏散平台，验证了多层次应急疏散模型的可行性。

关键词:多层次疏散模型；空间点配对；最优K条路径；车辆分配；应急疏散平台

近几年全球灾害频发，如何应对灾害条件下的应急疏散，成为国内外研究的热点。1960年代起世界各国的科研工作者就提出了很多应对不同灾害类型的应急疏散模型，1970年代 Lewis[1]提出飓风交通预测需求方法，1980年代美国的弗吉尼亚州为应对核泄漏开发出一套应急疏散仿真系统(NETVACI)[2]，1990年代又开发了TEDSS决策支持系统，以防止核电站发生灾害后及时通知当地群众撤离路线[3]，Cova等[4]对野火蔓延区域的家庭进行了模拟，并估算比较了为家庭疏散所推荐的撤退路线的疏散时间。国内学者通过总结中国历年来遭遇重大灾害后应急救援的经验和教训，提出用理性战略来实施应急救援的总体布局[5]，通过构建异地疏散专题模型和地震应急空间信息库，为地震应急指挥决策确定应急疏散的最优方案[6]，同时对应急疏散的最优路径进行了研究[7]；除此之外，李清泉等人[8]提出基于拥挤度的应急疏散路径优化方法，为大型公共场所人员提供疏散路径方案。

随着计算机仿真技术的发展，发达国家逐渐采用宏观和微观交通仿真技术对紧急事件疏散方案进行分析评价[9-12]，如苏格兰开发的多层建筑物/人员疏散模拟软件SIMULEX，英国开发的火灾模拟软件SMARTFIRE与大型场馆人员疏散模拟软件EXODUS，美国橡树岭国家实验室针对飓风等紧急事件应急疏散开发的大型路网应急交通流疏散模拟系统OREMS，以及MIT开发的多用途大范围道路交通综合仿真软件TransModeler等。这些都是针对西方欧美国家灾害发生后，在政府发布的灾害信息和交通诱导下，受灾群众进行自主驾驶，逃离灾害区域的疏散模式，应急疏散主要涉及到灾害人数、位置、区域以及疏散路径的选择；而我国在大型灾害条件下，应急疏散以集体转移疏散为主，主要依靠政府统一安排和组织，将受灾群众集中在危险区域的若干集结点，统一安排车辆疏散到安全区域的若干个安置点，是一种集体转移疏散模式，主要涉及到受灾人数、灾害的位置、区域的定位，集结点、安置点的选择和空间和人数配对，以及集结点到安置点的转移路径、车辆数和人数。因此，现有的应急疏散模型无法满足中国灾害应急的集结点、安置点的空间和人数配对、路径选择、转移人数、转移车辆数等。

本文针对中国灾害条件下应急疏散的需求，构建从危险区域的多集结点到安全区域的多安置点的多层次应急疏散模型，确定集体疏散人员的疏散路径、人数和车辆数，实现在最短时间内的人员整体最优疏散。

1道路疏散能力评估

灾害条件下将危险区域的人员疏散到安全区域的主要目标是高效和安全。高效性是指在最短的时间内将所有人员从集结点转移到安置点，期间涉及了道路的等级、车辆限速、路段长度、车流状况。安全性则是指从集结点将待疏散人口转移到安置点的过程中要穿越危险区的一部分地区，由于灾害的发生会导致建筑物坍塌、路面损毁、山体滑坡等危险情况发生，所以要保证疏散人员整体的安全性。因此，应急疏散应该选取道路通行能力最好、阻抗性最低的道路。基于以往的道路网数据分析和研究，道路阻抗性指标的计算有多种方法[13-14]。我们结合物理学中弹簧弹力模型：F=k×△x的物理意义和特性，提出以道路阻抗性作为衡量道路疏散能力的评估依据，当道路阻抗系数不变时，道路越长道路阻抗力就越大。同理如果两条路径长度相同，但阻抗系数不同的道路，阻抗系数越大的道路其阻抗力就越大。道路阻抗性需要两个方面因素来确定：一是由道路等级、车辆限速、路面宽度以及车流量等确定的通行阻抗；二是由灾害发生导致路面塌陷、断裂和阻挡导致的灾害阻抗。根据上述分析，构建道路阻抗Pi如下：

Pi= a1×Ti+a2×Di。

(1)

式中：Pi为某条路段的阻抗；Ti为某路段的通行阻抗；Di为某路段路面损毁程度决定的损毁阻抗；a1、a2为通行阻抗和损毁阻抗系数，分别用来确定Ti与Di的影响因子比例以及平衡两者之间的量纲问题，其大小由专家经验和实际道路交通状况而定。

依据我国九五交通科技重点攻关项目研究成果重新标定的BPR函数，并结合灾害发生后所需的实时信息的支持，对BPR函数的各个参量做了一定的调整，公式如下所示：

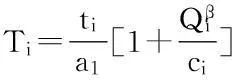
(2)

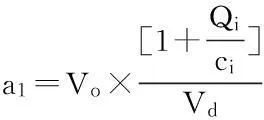
(3)

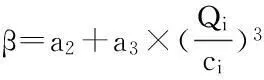
(4)

式中：Ti表示了路段i在实时速度为Vo的时候行驶整条路段所需要的时间；Qi(pcu/h)是路段i的实时交通流量；Ci(pcu/h)为路段i的通行能力；ti则基于道路i的设计车速的行驶时间；Vo(km/h)是路段i的实时行驶速度；Vd(km/h)为路段i 的设计车速其值的大小与道路等级相关；a1, a2, a3, β为回归参数和修正系数，其值的大小本文引用了文献[15]中通过大量道路数据研究所获得的经验值。

灾害阻抗往往和灾害的类别、发生区域地理环境以及经济状况有很大的关联。相对于城市而言，复杂的道路网以及密集的建筑群都会为灾害的疏散带来一定的困难；山地区域的灾害则需要考虑路网的便利性，诸如泥石流、山洪、地震等灾害也许会破坏仅有的几条交通要道，从而阻碍疏散的完成。通过分析这些因素我们基于现有针对城市地震灾害阻抗计算公式，提出了其在其他区域内的应用变形，如下所示：

Di=Pbi×Si×Ei。

(5)

式中：Di是路段i的灾害阻抗值；其单位为m；Pbi为路段i两侧分布物体被破坏的概率；Si为路段i的阻断严重性；Ei为路段i的阻断曝光量。

Si=Hi/Wi。

(6)

式中：Hi为路段i两侧分布物体的平均高度，Wi为路段i的道路有效宽度。

Ei=Ki×Li。

(7)

式中：Ki是路段i两侧分布物体的密度；Li是路段i的长度。

2多层次应急疏散模型

多层次应急疏散模型是根据灾害发生的具体位置，受灾群众人数，集结点和安置点位置，确定危险区域与实时道路网疏散能力，确定多集结点与多安置点之间空间配对和人口数量，完成多源多汇的路径优化，并根据疏散车辆总数和疏散路径，分配每一条疏散路径上的车辆数和疏散人数。

2.1多集结点与多安置点之间的空间匹配

将滞留在危险区域集结点的居民疏散到安全区域安置点是构建多层次模型的主要任务，首先要根据集结点与安置点之间的空间位置和人口数，确定集结点和安置点的空间匹配方案。根据具体位置与灾害范围，确定危险区域，选取危险区域的多集结点和安全区域的多安置点。集结点选取是在危险区域内选取易于聚集人群、没有高大建筑物、尽可能远离灾害发生的源点、交通枢纽发达等特点的地方；安置点的选取是在远离危险区域的安全区域内选取救援物资运输便利、受伤群众可及时救治，最大程度接纳被疏散人员的地方，通常选取医院、学校、体育馆、广场等作为安置点。集结点和安置点的空间位置确定后，从空间分析角度进行多集结点和多安置点的匹配。

(1)集结点与安置点的Voronoi图构建

集结点与安置点的Voronoi空间分析是基于集结点与安置点的位置和形态特征，从空间位置、空间分布、空间形态、空间距离及空间方位、拓扑及相关等方面，采用Voronoi图的空间剖分特性，解决从多集结点到多安置点的配对问题。

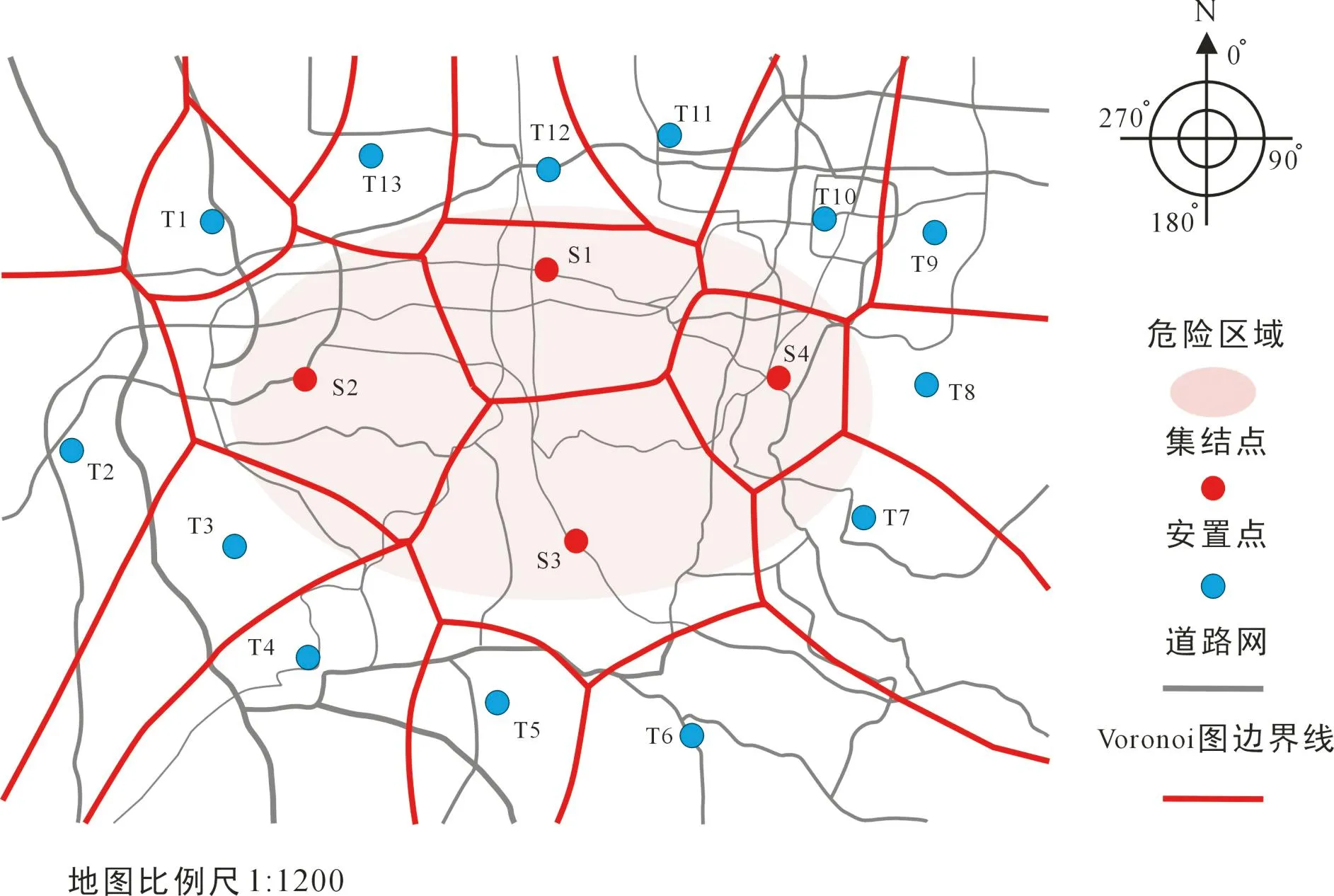
Voronoi图对平面N个离散点而言，它把平面分为几个区，每一个区包括一个点，该点所在的区是到该点距离最近点的集合，构建平面上若干点构成的多边形的内点到该多边形生距离。考虑到位于危险区域的集结点的待疏散人口数量和分布密度，以及位于安全区域安置点可接纳人口数量，采用加权Voronoi图进行空间剖分，生成加权Voronoi图，设n个点P={p1,p2,p3…pn},有n个正实数 λ={λ1,λ2,…},VORn=n(Pi, λi)=∩{P|d(p,pi)/λi

图1　Voronoi图与道路网络的叠加示意图

图1中的椭圆形中心为灾害发生地，其覆盖范围为危险区域，Si为危险区域的集结点，Ti为安全区域的安置点。

(2)多集结点到多安置点的空间配对

按照构建加权Voronoi图的方法和模拟点的坐标值及其权重值构建加权Voronoi图与道路疏散能力的道路网进行叠加，根据叠加后相邻关系来分析空间点之间的空间匹配关系，如图1所示,可以看到构成每个点辐射区域的多边形的邻近关系，按照这些点所在区域道路网通行能力以及每个集结点的待疏散人口数量和每个安置点可接纳人口数量，选取每个集结点所对应的若干个安置点。根据图1中所示，可以得到集结点与安置点的空间匹配。

表1所示为多个集结点和多个安置点的空间邻接关系，其中0表示两个点空间不邻接，1表示两个点空间邻接。根据表1所示的各个空间点的空间关系，可以得到与每个集结点所邻接的安置点。

表1　集结点与安置点的空间邻接表

根据各个集结点的空间拓扑关系和道路网疏散能力的高低，可以生成表2。从表2中可以看到，根据模拟值S1处待疏散人口数量以及所优先考虑的安置点：T10、T11、T12、T13每个安置点的接纳人口数量，最终确定的与S1配对的安置点分别为：T11、T12、T13，由于配置人口从优开始，所以T12、T11点的接纳能力达到满负荷，T13处的空余接纳人口数量则是S1处输送完T12和T11后剩余人口数量和T13原有接纳量之间的差值。按照以上分配人口的方法确定与每个集结点所匹配的所有安置点以及分配到各安置点的人口数量。

表2　基于道路权重的最终集结点和安置点配对表

2.2集结点到安置点的多源多汇路径优化

将受灾人员从集结点转移到安置点通常有很多条路径供选择，如何选择最优的路径使得受灾人员从集结点可以安全、高效到达安置点是构建应急疏散模型中及其重要的一个环节。基于加权Voronoi图和道路网叠加所获得的空间匹配关系，可以得到与每个集结点相匹配的若干个安置点以及从各个集结点出发到达每个安置点所分配的人口数量，一般情况下如果只选择一条路径作为从一个集结点到另一个安置点的疏散路线会导致该疏散路径上出现拥堵现象，从而加剧了道路的疏散压力直接导致整体疏散时间的延长。本文采用基于最大流[16-19]的K条路径优化方法，根据道路疏散能力的评判标准，选取从多个集结点到多个安置点的最优若干条路径，将多源、多汇问题转化为单源、单汇问题，也即最优K条路径，其基本思想为：从一个集结点出发到达另一个安置点有若干条道路，每条道路都由若干条路段组成，根据路段道路阻抗性高低来确定从集结点到安置点的每条通达路线的总阻抗，选取阻抗最小的路径作为最优路径，然后依次类推选取次优条、再次优条路径直到选取K条路径。

2.2.1最大流约束下的多路径优化

评定所选择区域内路段的疏散能力是建立在实时动态的交通流信息、道路损毁度和静态道路状况的基础上，为了实现在灾害条件下人员疏散的过程中所选择的道路具有实时的最优性，采用基于最大流的K条最优路径来解决短期内人员拥堵导致车流量增大从而影响全局的疏散速度的问题。将每条路段的人口分配信息记录在链接路段的节点上，如图2所示。图中路段权重采用道路阻抗性的倒数进行评定记为：p1，p2，p3…分别为每条路段的权重值，n1-2则为链接节点1和节点2的路段所分配的人口数量。

图2　基于最大流的多源多汇多路径和人流量优化分配

路段1～21～32～42～5……道路疏散能力p1p2p3p4……分配人口数n1-2n1-3n2-4n2-5……

根据图2所示，从集结点出发有三条路径可供疏散滞留人口到达安置点，三条路径分别经历了不同的道路节点分别为：{1,2,4,7,9}，{1,2,5,8,9}，{1,3,6,9}，根据图中的路段和节点的空间关系以及与分配人流量之间的关系得到表3，如下所示。

2.2.2道路网疏散能力分层与K路径层次搜索

由于路径优化过程中的路径搜索需要面对的是大区域的、实时的和包含POI信息的道路网数据，导致基于最大流的K条最优路径效率低，传统的路径寻优算法虽然都能实现单源点到单汇点的最短路径搜索，但是对于一些特定的问题却存在其自身的缺陷，Dijkstra算法是最短路径寻优算法中比较经典的一种算法，其优点是该算法实现起来容易简单，缺点是利用该算法寻找起讫点之间最短路径的过程中，需要遍历所有的节点和路段，极大地降低了搜索效率。对于小范围的数据该算法具有很好的应用性，但是对于大区域、海量的数据，就会大大降低整体模型的运算速度。针对路径搜索算法的优化，已经提出了很多新的方法[20-21]。本文则是按照特定的道路网数据格式和构建重大灾害条件下应急疏散模型的具体要求对数据进行分层处理，从而达到优化路径搜索的目的，如图3所示。

图3　道路网应急疏散能力分层与路径层次搜索

所有的道路网数据按照道路通行能力分为四个层次分别为：H={H1，H2，H3，H4},其中每个层都有各自的道路通行能力阈值范围：ζ={ζ1，ζ2，ζ3，ζ4}，其中对应的每个层都存在阈值范围：ζ1={ζ1min,ζ1max},ζ2={ζ2min,ζ2max},ζ3={ζ3min,ζ3max},ζ4={ζ4min,ζ4max}。对于道路网层：Li=(Vi, Ei, Wi, ζi)，速度Vi=(v1,v2…)，阻断曝光量Ei=(e1,e2…); 通行能力ζi=(ζimin, ζimax)，当搜索某一个集结点到另一个安置点的通达路径时，按照如下步骤实施。

Step1：判断集结点和安置点所临近的路段的等级，采用“选高不选低”的原则将该集结点和安置点配置到与其临近的所有路段中等级最高的路段上。

Step2：从集结点出发寻找与之共线的其他节点，并判断这些节点所位于路段的层级，假设与集结点位于同一条路段的节点集合按照所在道路等级从高到低的顺序进行排序得到集合N={ n|ni∈Ls，i=1,2……}。

Step3：从集合N中依次取每个节点元素进行下一步的搜索，若当前节点所在的路段位于最高层级，则从该节点所在的路段开始，寻找与之共线的下一个节点，并将该路段作为可用路段进行标记，然后将下一个节点作为当前节点开始下一步搜索，依次类推直到当前节点与安置点匹配路段后的对应节点位于同一条路段上停止搜索。

Step4：若从集结点出发无法再找到可以与之链接的高层级路段的节点时，则选择次优层级作为搜索目标，寻找当前节点所位于层级的下一层层级相对应的节点，再从该节点出发搜索直到到达安置点为止。

Step5：重复Step3、Step4，直到节点集合中的各个元素都搜索完毕为止，并将从出发节点到终止节点途径的所有节点与路段标记与记录形成点-路段-点，即以路径为主的文件。具体搜索方法如图4所示：从集结点出发，将该集结点配置到L1路段上，然后判断与集结点共线的下一结点，从该节点出发寻找下一条到达安置点的路径。由于在Hi层级上已经无法找到可以到达安置点的路段，则从该层级的那个终止节点出发找到其位于Hi+1层级的对应点，然后根据该对应点所位于路段的拓扑关系，找到到达安置点的通达路径。图3中从集结点出发到达安置点的路径都由黄色的箭头标示出来。

2.3K路径的疏散车辆数分配

多层次应急疏散模型的最后就是要在和多源多汇规划的K路径基础上，根据每一条路径上的待疏散人数和基于道路疏散能力，确定K路径上的车辆数。通过路径搜索和节点人流分配，可以得到从某个集结点到某个安置点的K条最优路径中每条路径的所分配到的疏散任务也即疏散的人口数量。假设从某个集结点出发到达某个安置点有k条路径，分配给每条疏散路径上的人口数量分别为：{Q1，Q2，Q3，Q4…Qk}。根据疏散路径的长度和实时运输速度，计算出每条疏散路径的单次疏散时间ETi(第i条路上单次疏散时间)，假设有k条疏散路径，每条路径的单次疏散时间表示为：{ ET1，ET2，ET3…ETk}，a为每车能疏散的人数，根据应急疏散的整体最优为目标，建立车辆分配的目标函数如下：

(8)

当单条路径的疏散时间接近与所有应急疏散路径所完成疏散的时间的平均值时，可以将此状态作为应急疏散达到整体最优，也即在上述公式中目标函数F的值无限趋近于0的时候，所求出的车辆数量即为每条疏散路径疏散人口的最优疏散车辆数，在采用计算机模拟计算时，可以将F值取为0从而得到每条路径的车辆分配数量。

假设从所有的集结点到所有的安置点共有K条路径，每条路径的单次疏散时间为ETi；假设每辆车可以运载a人，则每条路上分配到的车辆数为Nk，车辆总数为N；ni为第i条疏散道路所有的路段数量为n，tij则为第i条路上第j个路段的单次疏散时间。

N=N1+N2+…Nk；

(9)

(10)

(11)

3实验与比较

3.1实验

本文以GoogleMapAPI为开发平台，采用C#开发完成了大范围的多层次应急疏散平台。以国家“八六三”计划项目的示范区域山东省德州市为实验，采用基于无人机等低空遥感平台采集的实时交通信息，以及灾害区域内的道路损毁信息，假设山东德州发生地震，获取到了实时交通信息及灾害损毁信息，采用本文提出的多层次应急疏散模型，确定危险区域，选取集结点和安置点，整个实验区的道路网G={V，E，W}，其中路网的实时速度V={v1,v2,v3…}，阻断曝光量E={e1,e2,e3…}，道路通行能力W={w1,w2,w3…}，确定道路通行能力值依次存入到W集合中，并与V，E相对应，建立实验区的道路网拓扑，以及对道路网的疏散能力进行评估。

圆形覆盖的区域中心为灾害点，圆形区域为灾害区域，选取山东德州市的4个集结点：S1、S2、S3、S4，ID号分别为41、55、49、54，以及8个安置点：T1，T2，T3，T4，T5，T6，T7，T8，ID号依次为：24、237、76、75、238、9、8、4。通过多层次应急疏散平台，将道路网和依据集结点和安置点所构建的Voronoi实现图层叠加，如图4所示，根据其空间匹配关系，得到的集结点和安置点的配对信息表存入到实时数据库中。根据多层次应急疏散模型，实现集结点到安置点的K条最优路径优化与车辆分配，生成应急疏散路径、疏散人数、车辆分配，具体如图5所示。

图4　集结点与安置点的Voronoi图与空间匹配关系示意图

图5　应急疏散路径与车辆分配结果

图5中淡蓝色圆形覆盖的区域为设置了中心灾害源后所定义的模拟灾害区，位于灾害区域内的黑色圆点为模拟决策者选取的集结点，位于安全区域内的红色三角形为安置点。按照系统自动对所有的集结点和安置点赋予ID标示，图中;ID号为：41、55、49、54是集结点的ID号，ID号为：24、237、76、75、238、9、8、4是安置点。由于本文实验所用基础路网与Googlemap基础路网存在差异性，所以每一条路径并没有完全的与其重叠。并且多源-多汇分配方案可以从图中读取，具体内容如表4所示。

表4　应急疏散人口分配及车辆分配方案表

3.2与国内外方法的比较

欧美国家发生灾害后，受灾群众会驱车自主疏散。由于我国目前私家车普及率低且人口数量、密度大，所以采用国外应急疏散模式并不适用我国国情。因此，本文所提出的模型主要针对我国某些区域发生大型灾害后，政府将受灾群众集体式的从危险区域内多个集结点转移到安全区域内的多个安置点。同时我们提出的多层次应急模型和疏散方法是针对灾害定位、道路灾害损毁和疏散能力评价方法、集结点和安置点选取与空间配对、多集结点和多安置点人口持有率和容纳量的配比及疏散路径的优化、以及基于疏散时间最短的全局最优条件下每条疏散路径上车辆分配。与国外现有应急疏散模型或方法的对比主要体现在：应对灾害类型、确定灾害范围功能、集结点和安置点选取、疏散路径推荐、车辆分配等，具体对比内容如表5所示。

从表5中可以看到，欧美发达国家现有的应急疏散模型大部分针对飓风、核电站、室内火灾等易发灾害，而我国目前面临最严重的灾害就是地震及地震引发的次生灾害。针对应对灾害类型的不同，所适用的应急疏散模型功能、机制也会有所不同。

4结论

针对我国灾害条件下高密度人口的集体疏散模式，以道路实时速度和路面损毁程度所决定的道路阻抗性作为评判道路疏散能力的依据，提出了从多集结点到多安置点的多层次应急疏散模型，确定待疏散群众的疏散路径、人数和车辆数，并以山东省德州市作为实验区域，采用GoogleMap API和C#搭建多层次应急疏散平台。与国内外应急疏散模型进行比较和分析，验证了该模型对国内国情的适用性较高且应对细节更加丰富。对于中国集体疏散模式下应对各种自然灾害的应急疏散，目前的研究只是刚刚开始，尤其是对于大规模和大区域范围的应急疏散仿真将有待进一步的研究。

表5　本文方法与国内外方法比较

参考文献：

[1]Lewus D C. Transportation planning for hurricane evacuations[J]. ITE Journal, 1985,55 (8)：31-35.

[2]Hobeika A G, Kim C. Comparsion of traffic assignments in evacuation modeling[J].IEEE Transactions on Engineering Management, 1998, 45(2):192-198.

[3]Hobeika A G, Kim S, Beckwith R E. A decision support system for developing evacuation plans around nuclear power stations[J].Interfaces,1994,24(5):22-35.

[4]Cova T J, Johnson J P. Microsimulation of neighborhood evacuations in the Urban-wildland Interface[J].Environment and Planning, 2002,34(12): 2211-2229.

[5]张玮晶.特大地震灾害应急救援中理性战略的建立与实施[J]. 灾害学, 2014,29(4): 155-158.

[6]曹彦波，李永强，曹刻,等. 基于GIS技术的地震应急异地疏散接受能力判断模型研究[J]. 地震研究，2008，31:624-628.

[7]刘春年，邓青箐. 应急决策信息系统最优路径研究——基于路阻函数理论及Dijkstra算法[J]. 灾害学，2014,29(3):18-23.

[8]李清泉，李秋萍，方志祥.一种基于时空拥挤度的应急疏散路径优化方法[J].测绘学报，2011,40(4):518-522.

[9]Wang Z., Jia F, Galea E R. Simulating one of the CIB W14 round robin test cases using the SMARTFIRE fire field model[J]. Fire Safety Journal, 2001, 36(7):661-677.

[10]Cwynne S, Gelea E R. Arcview of the methdologics used in the computer simulation of evacuation from the build enviroment[J]. Building and Enviroment, 1999, 34:741-749.

[11]Yu J, Pande A, Nezamuddin N, et al. Routing strategies for emergency management decision support systems during evacuation[J]. Journal of Transportation Safety & Security, 2014, 6(3): 257-273.

[12]Lu L, Yun T L, Li L.A comparison of phase transitions produced by paramics, transModeler, and VISSIM[J]. IEEE Intelligent Transportation Systems Magazine, 2010,2(3):19-24.

[13]王元庆，周伟，吕连思. 道路阻抗函数理论与应用研究[J].公路交通科技，2003,21(9):82-85.

[14]王炜,邓卫杨琪,等著. 公路网络规划建设与管理方法[M].北京：科学出版社，2001,101-103.

[15]许添本,吕奖慧. 地震救灾最小风险路径选择模式之建立与应用[J].国立台湾大学台大工程学刊，2002,85:32-47.

[16]Ahuja R K, Magnanti T L.Network flows: Theory, algorithms and applications[M].New Jersey: Prentice Hall.2000:34-78.

[17]Chang J C, Cheng R C, Shih H T, et al. Maximum freedom last scheduling algorithm for downlinks of DSRC networks[J], IEEE Intelligent Transportation Systems Society, 2007,8(2):223-232.

[18]颜佑启，欧阳建湘. 最短路-最大流交通分配法[J]. 中国公路学报，2005,18(4): 91-95.

[19]向剑平，王悦，胡剑. 基于道路网络的首先优化路径搜索算法[J]. 计算机工程，2011,37(12):54-55.

[20]唐炉亮,常晓猛,李清泉. 出租车经验知识建模与路径规划算法[J]. 测绘学报, 2010, 39 (4):404-409.

[21]Maher L, Tiravat A, Siamak A. A dynamic transportation planning support system for hurricane evacuation[C]//2006 IEEE Intelligent Transportation Systems Conference. Toronto, Canada, 2006:612-617.

杜爱军,魏鸣,王炳赟. 下击暴流的三维仿真和回波特征分析[J].灾害学, 2015,30(2):186-192,234. [Du AiJun, Wei Ming and Wang Bingyun. Three-dimensional simulation and echo characters analysis on downbursts[J]. Journal of Catastrophology, 2015,30(2)：186-192,234.]

Research on the Multi-levels Emergency Evacuation Model underDisaster Conditions

Tang Luliang1, Yang Xue1, Liu Zhang1, Wang Xuehao1, Jin Chen1and Dong Kun2

(1.StateKeyLaboratoryofInformationEngineeringinSurveying,MappingandRemoteSensingof

WuhanUniversity,Wuhan430079,China; 2.AerospaceHengxinTechniqueLLC(503Institute),

Beijing100086,China)

Abstract:So many major disasters happened in the world every year and lead to serious loss to the property and personal safety. How to formulate emergency evacuation model for high-density city under the disasters condition is very important for human being. China has many high-density cities and when the disaster happened people there will be delivered by the government. So the difference between other developed countries and China is the evacuation model belongs to a kind of collective evacuation. Multi-level Emergency Evacuation Model (MEEM) is put forward, which determines the space match between the multi-gathering places (Origins) in the disaster area and multi-setting places (Destinations) in the safe area. Based on the real road traffic and road damage in varying degrees, MEEM measures the road evacuation ability use the road impedance which is decided by road speed and pavement damage limited to the evaluation target. MEEM plans the routes from the Origins to the Destinations, and decide the numbers of the evacuation cars and population on the every route. Finally, an emergency evacuation case has been done in this paper with the data base of Shandong province, and a function compare has been done between the proposed model with other evacuation models, and the result validates the MEEM to be a promising method which fits to the Chinese condition.

Key words:Multi-level Emergency Evacuation Model; spatial point matching; the optimal K path; vehicle allocation; emergency evacuation platform

doi:10.3969/j.issn.1000-811X.2015.02.035

中图分类号：P208 ；X43

文献标志码：A

文章编号：1000-811X(2015)02-0179-07

作者简介：唐炉亮(1973-)，男，湖南湘潭人，博士(后)，教授，博士生导师，主要从事时空GIS、交通地理(GIS-T)，时空数据获取与分析等研究. E-mail: tll@whu.edu.cn通讯作者：杨雪(1989-),女，宁夏银川人，博士研究生，主要从事时空数据获取、处理和分析.E-mail: yangxuez@126.com

基金项目：国家自然科学基金资助项目(41271442,40801155)；中国航天科技集团公司卫星应用研究院创新基金资助(2014CXJJ-DSJ02)；深圳市北斗卫星应用工程技术研究中心资助

收稿日期：2014-10-28修回日期：2014-12-04