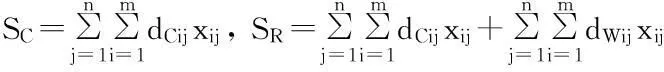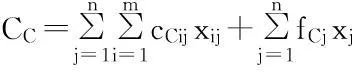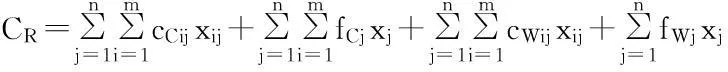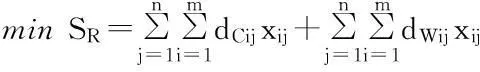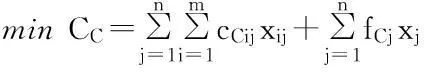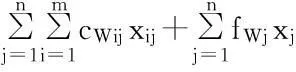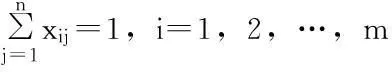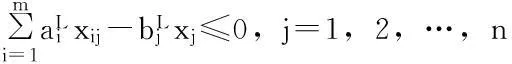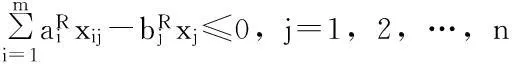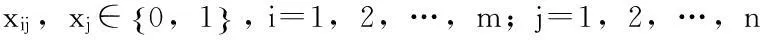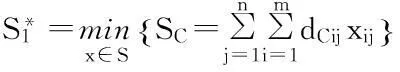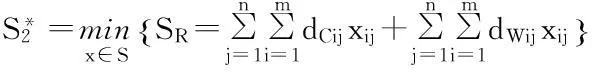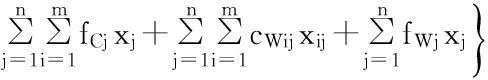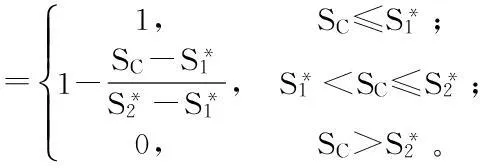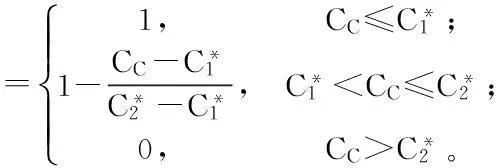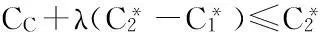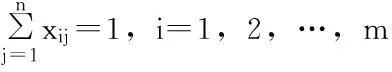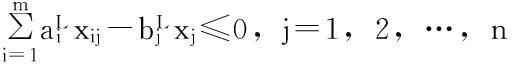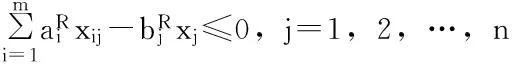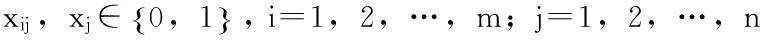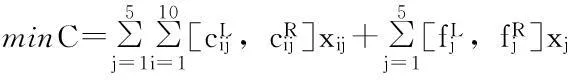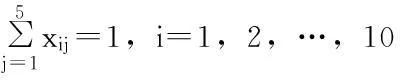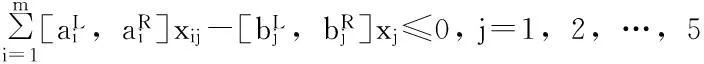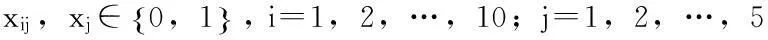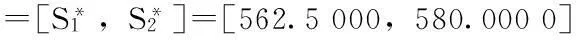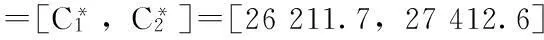基于区间数信息的区域应急物资储备库选址多目标决策模型*

郭子雪，王兰英， 齐美然，张　露

(1.河北大学 管理学院，河北 保定 071002； 2. 河北大学 期刊社， 河北 保定 071002)



基于区间数信息的区域应急物资储备库选址多目标决策模型*

郭子雪1，王兰英2， 齐美然1，张露1

(1.河北大学 管理学院，河北 保定 071002； 2. 河北大学 期刊社， 河北 保定 071002)

摘要:应急物资储备库选址决策是区域应急物资储备体系建设中的重要问题之一。该文研究了基于区间数的区域应急物资储备库选址问题的模糊多目标决策方法，给出了区间数的概念和排序规则，构建了约束条件中含有区间数的区域应急物资储备库选址问题的模糊多目标规划模型，提出了求模型满意解的算法，最后通过算例分析说明该方法的有效性。

关键词:应急物资储备库；区间数；选址模型；模糊多目标决策

应急物资储备库选址决策直接关系到应急物资保障的反应速度和区域应急物资储备体系建设的有效性。应急物资储备库选址决策属于设施选址问题的研究范畴，目前，国内外学者对应急物资储备库选址问题的研究主要集中在该类问题的集合覆盖模型[1-3]、最大覆盖模型[4-5]、多目标决策模型[6]、随机规划模型[7-8]、多属性决策模型[9-11]以及模型的算法设计[12-13]等方面。本文在现有研究基础上，构建了区间数信息下应急物资储备库选址问题的模糊多目标决策模型，给出了模型的有效解法。

1区间数及其排序规则

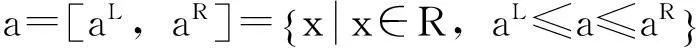
(1)

定义2设a=[aL,aR],b=[bL,bR]是两个区间数，λ为实数，则有

①加法运算a+b=[aL,aR]+[bL,bR]=[aL+bL,aR+bR]；

(2)

②减法运算a-b=[aL,aR]-[bL,bR]=[aL-bR,aR-bL]；

(3)

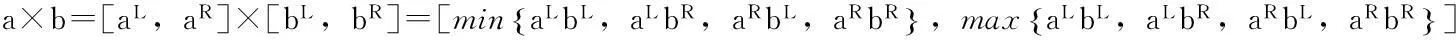
(4)

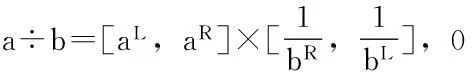
(5)

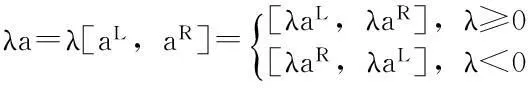
(6)

定义3[14]设a=[aL,aR],b=[bL,bR]是任意两个区间数，定义a和b之间的序关系“≤LR”：

(7)

序关系“≤LR”表示：在最小最优化问题中，决策者希望实际问题产生较小的消耗，如果a≤LRb，则a优于b。

定义4[14]设a=[aL,aR],b=[bL,bR]是任意两个区间数，定义a和b之间的序关系“≤CW”：

(8)

在定义4中，区间数a的中点aC反映区间数a的期望值，区间数a的半径aW反映区间数a的不确定性。在最小最优化问题中，决策者追求最小消耗和最小不确定性，即如果a≤CWb”，则a优于b。

定义5设a=[aL,aR],b=[bL,bR]是任意两个区间数，定义a和b之间的序关系“≤CR”：

(9)

容易证明：

(10)

2问题描述与模型构建

2.1问题描述

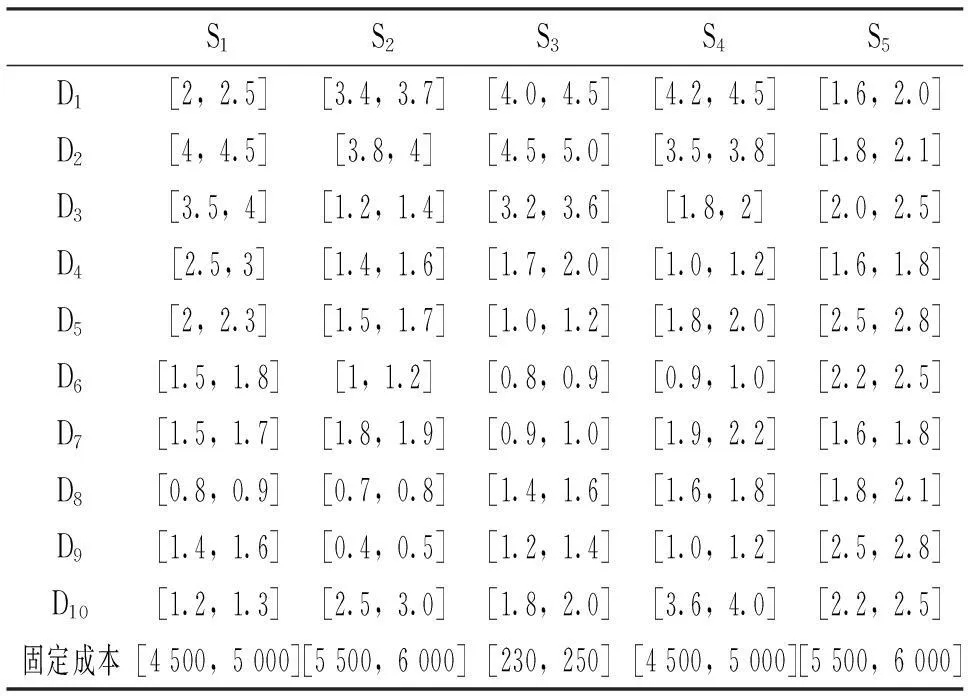
设S1,S2,…,Sn为应急物流系统中n个可供选择的应急物资储备库选择点，D1,D2,…,Dm为该应急物流系统的m个应急物资需求点。由于突发事件的应急管理具有复杂性、不确定性等特点，所以假设应急物资储备库选择点到应急物资需求点的行车距离、运输费用、各需求点的需求量以及每个应急物资储备库选择点的容量等系统决策参数均可用区间数来表示。那么在应急物资储备库的容量受限条件下，应如何选择应急物资储备库的位置，才能使该应急物流系统运行总成本和应急物资储备库到达各应急需求点的总距离达到最小？

根据突发事件应急管理的特点，本问题的讨论作如下假设：

(1)该问题的目标函数和约束条件都是决策变量的线性关系，且其中的不确定性系统参数均为区间数形式。

(2)系统中的应急物资储备库候选点是确定的，每个应急物资储备库候选点的建设成本各不相同，且其应急物资储备具有容量限制。

(3)突发事件发生后系统中应急需求点的需求量可以预测，各需求点的需求总量小于或等于系统中各应急物资储备库的储备总量。

(4)考虑到突发事件发生后道路交通状况会受到多种客观因素的影响，从应急物资储备库到应急需求点的运输距离是一模糊变量，用区间数表示。

(5)要求每个应急需求点由一个应急物资储备库提供应急服务，不考虑应急物资装卸过程中消耗的时间。

(6)为了兼顾应急物资储备库的可及性以及资金受限条件下资金的利用效率，问题的目标是使应急物资储备库到达应急需求点的总距离、应急系统总的运营成本最小化。

2.2模型的建立

(1)模型参数的涵义

n表示应急物资储备库候选点的个数；

m表示应急需求点的个数；

i表示应急需求点集数量m的索引号；

j表示应急物资储备库候选点集n的索引号；

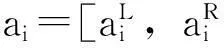
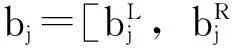
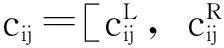
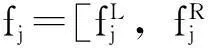
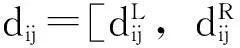
xij是0-1决策变量，当需求点i由应急物资储备库候选点j提供服务时它取值为1，否则它取值为0。

xj也是0-1决策变量，当应急物资储备库候选点被选中时它取值为1，否则它取值为0。

(2)问题的数学模型

基于上述假设，可得应急物资储备库选址问题的模糊多目标规划模型：

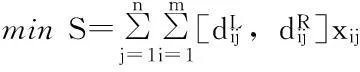
(11)

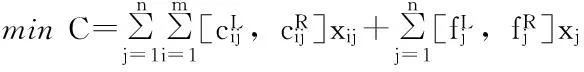
(12)

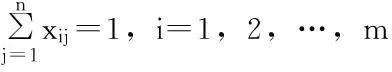
(13)

xij-xj≤0,i=1,2,…,m;j=1,2,…,n；

(14)

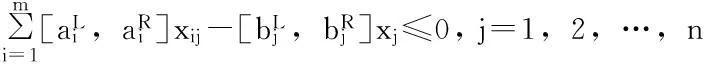
(15)

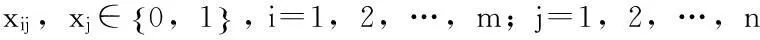
(16)

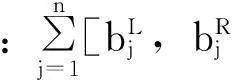
3模型算法

3.1约束条件的确定性转化

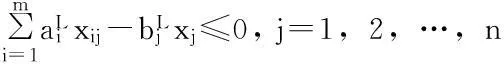
(17)

(18)

于是，模糊多目标规划问题(1)～(6)等价于以下模糊多目标规划问题(P1)：

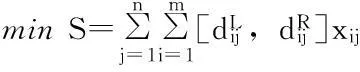
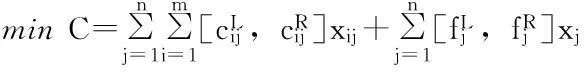
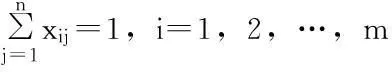
xij-xj≤0,i=1,2,…,m;j=1,2,…,n；

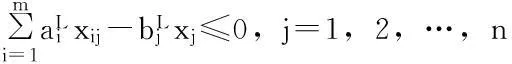
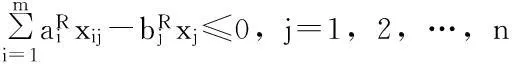
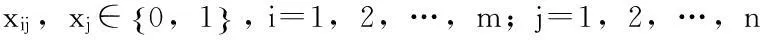
3.2模糊多目标规划问题的确定性转化

定义6设K是模糊线性规划问题(1)～(6)的可行解集，x0∈K是它的一个最优解，如果不存在另一个x∈K，使得S(x)

假设SC,SR分别表示区间型目标函数S的中点和半径，CC,CR分别表示区间型目标函数C的中点和半径，则根据区间数的运算得到：

由模糊多目标规划问题(1)～(6)得到以下普通多目标规划问题(P2)：

xij-xj≤0,i=1,2,…,m;j=1,2,…,n；

可以证明：问题(P2)Pareto最优解即是模糊多目标规划问题(1)～(6)在定义6下的最优解。

分别考虑问题(P2)中的每个目标函数，利用普通单目标规划问题的解法可以得到其最优解和最优值。

于是得到模糊多目标规划问题(1)～(6)目标函数S和C的容许区间：

(19)

定义区间数目标函数S小于S*、C小于C*的满意度：

(20)

(21)

采用极小算子，可得与问题(P2)等价线性规划问题(P3)：

(P3)：maxλ；

xij-xj≤0,i=1,2,…,m;j=1,2,…,n；

3.3模型算法的一般步骤

Step1利用序关系“a≤CRb”，写出经典多目标规划问题(P2)；

Step2针对多目标规划问题(P2)中的每个目标函数，求解相应的单目标规划问题，得到模糊多目标规划问题(1)～(6)各目标函数的最好值(或期望值)与最差值；

Step3定义每个目标的隶属度函数，构建单目标参数规划问题(P3)；

Step4求解单目标参数规划问题(P3)，得到原模糊多目标规划问题(1)～(6)的Pareto最优解。

表1　应急物资储备库的容量及其到需求点的距离等

表2　应急物资储备库的固定成本及其到需求点的单位运费

4算例分析

设0-1决策变量xj=

xij-xj≤0,i=1,2,…,10;j=1,2,…,5；

利用表1和表2中的数据计算出dCij,dWij,cCij,cWij，代入问题(P2)并求解，可得目标函数S和C的容许区间：

将上述结果代入(P3)，并利用lindo软件求解，可得其最优解：λ=0.999 375 5，x15=1，x25=1，x34=1，x44=1，x53=1，x62=1，x73=1，x81=1，x92=1，x101=1，x1=1，x2=1，x3=1，x4=1，x5=1，其余为0；此时，SC=562.5，CC=26 212.45。

5结论

应急物资储备库选址问题是区域应急物资储备体系建设中的重要决策之一，将应急物资储备库置于合理的位置，不仅可以降低成本，而且能够保证提供应急物资的时效性，它直接关系到应急物流保障的反应速度和区域应急物资储备体系建设的有效性。本文基于区间数模糊信息环境，构建了约束条件中含有区间模糊参数的应急物资储备库选址多目标规划模型，提出了一种基于满意度的模型优化算法，并通过算例分析验证了该方法的可行性和有效性。

参考文献：

[1]何建敏，刘春林.应急管理与应急系统-选址、调度与算法[M].北京:科学出版社，2005.

[2]方磊.基于偏好DEA的应急系统选址模型研究[J].系统工程理论与实践，2006 (8):116-123.

[3]刘浪.基于集合覆盖理论的航空应急物资储备点选址方法[J].南昌航空大学学报，2010，12(2)：19-26.

[4]陈志宗,尤建新. 重大突发事件应急救援设施选址的多目标决策模型[J].管理科学，2006，19(40)：10-14.

[5]Adenso-diaz B, Rodriguez F. A simple search heuristic for the MCLP: Application to the location of the ambulance bases in a rural region[J]. Omege, 1997, 25: 81-187.

[6]陈达强，刘南．带时变供应约束的多出救点选择多目标决策模型[J]. 自然灾害学报，2010,19(3):94-99.

[7]Vladimir M, Charles R. The queuing probabilistic location set covering and sime extension[J]. Socio-Economic Planning Science, 1994, 28: 167-178.

[8]Mustafa S. Canbolat, Michael von Massow. Locating emergency facilities with random demand for risk minimization[J]. Expert Systems with Applications, 2011, 38:10099-10106.

[9]李国旗，张锦，刘思婧.城市应急物流设施选址的多目标规划模型[J].计算机工程与应用，2011，47(19):238-241.

[10]田依林.基于FAHP 法的应急物资储备库选址研究[J].武汉理工大学学报:交通科学与工程版，2010，34(2):354-357.

[11]王威. 城市避震疏散场所选址的时间满意覆盖模型[J].上海交通大学学报，2014, 48(1): 154-158.

[12]Carmen G Rawls, Mark A Turnquist.Pre-positioning of emergency supplies for disaster response[J]. Transportation Research Part B, 2010 (44):521-534.

[13]Beasley J E, Jomsten K. Enhancing an algorithm for set covering problems[J].European Journal of Operational Research, 1992, 58: 293-300.

[14]Ishibuchi H,Tanaka H. Multiobjective programming in optimization of the interval objective fuction[J]. European Journal of operational research, 1990,48:219-225.

陈伟珂，花翠. 基于突发事件生命周期视角的应急物流虚拟联合体的运行模型研究[J].灾害学, 2015,30(2):152-157. [Chen Weike and Hua Cui. Research on operation models of emergency logistics virtual union based on emergency lifecycle[J].Journal of Catastrophology, 2015,30(2)：152-157.]

A Fuzzy Multi-objective Decision Making Approach of EmergencyMaterial Storage Location Based on Interval Number

Guo Zixue1, Wang Lanying2, Qi Meiran1and Zhang Lu1

(1.SchoolofManagement,HebeiUniversity,Baoding071002,China; 2.EditorialDepartment

ofJournal,HebeiUniversity,Baoding071002,China)

Abstract:Emergency material storage location is one of the important problems for constructing regional emergency resources reserve system. A fuzzy multi-objective decision making approach of emergency material storage location based on interval number is studied. Concept and ordering rule of interval number are given. The fuzzy multi-objective decision making model of emergency material storage location based on interval number is set up, and the solution algorithm for this model is presented. Finally, a numerical example shows that the method is valid.

Key words:emergency material storage; interval number; location model; fuzzy multi-objective decision making

doi:10.3969/j.issn.1000-811X.2015.02.029

中图分类号：X43

文献标志码：A

文章编号：1000-811X(2015)02-0148-04

作者简介：郭子雪(1964-)，男，河北清河县人，教授，博士，主要从事物流与供应链管理、应急管理等方向的研究．E-mail：guozx@163.com通讯作者：王兰英(1978-)，女，河北衡水人，副编审，博士，主要从事项目投资决策、生物环境与能源工程方向的研究．E-mail: 15188936776@qq.com

基金项目：国家社科基金资助项目(11BGL089)；河北省社科基金项目(HB14GL076)

收稿日期：2014-09-02修改日期：2014-11-05