训练场地环境下杰出运动员中枢疲劳ANN预测模型的构建

周文婷++孟琪

摘要：目的：构建可预测训练场地环境综合因素影响下的杰出单板U型场地滑雪运动员中枢疲劳情况的人工神经网络模型（ANN）。方法：分3次对单板U行场地滑雪国家队在哈尔滨体育学院帽儿山滑雪场的训练场地环境指标进行测试，并对运动员的声喜好等情况进行问卷调查和访谈，测试及调查指标包括声学指标和环境指标。以闪光融合频率评价运动员的中枢疲劳情况。将上述指标纳入ANN模型的构建，包括训练次数、隐藏层设计、函数的选择和模型的检验等。结果：14个主、客观指标变量与单板U型场地滑雪运动员的中枢疲劳显著相关，2个不相关。在3层结构（1个隐藏层）的ANN模型中，隐藏节点数、训练次数和训练函数分别在25、800和TRAINOSS时效果最优。分别构建了可预测运动员中枢疲劳的ANN通用模型和分组模型，并获得了上述模型的最优网络参数及预测结果。结论：成功构建了可预测训练场地环境综合因素下杰出单板U型场地滑雪运动员中枢疲劳情况的ANN模型。

关键词：训练场地环境；综合因素；单板U型场地滑雪；中枢疲劳；预测；人工神经网络

中图分类号：G804 文献标识码：A

文章编号：1008-2808（2015）06-0008-07

作为技巧类难美项群雪上运动项目，单板U型场地滑雪因其运动员需要在3-4min内完成6-8个高难度空中翻转动作，故在训练和比赛中易因精神高度紧张，注意力集中而产生中枢疲劳。中枢疲劳是中枢为防止机体发生过度机能衰竭而出现的保护性抑制，可受多种因素影响并存在显著的个体差异，环境可能是其中一个重要因素。众多研究发现，环境声音对环境中个体的心理疲劳影响显著，其他环境因素则可能与环境声音协同发挥作用。

当前，主流的预测方法分为基于人工智能的预测方法和基于统计学的算法，前者包括支持向量机、贝叶斯网络和人工神经网络（artificial neuralnetwork，ANN）等，后者如序列逻辑回归模型。不同于以往的理论推导公式，ANN可通过分析和学习大量已有的评价数据，总结出研究对象与影响因素之间的关系，并由这些“关系”预测未知结果，在60余年的发展中，不断完善和加人多种算法，从而在工业、医学、商业等众多领域广泛用于识别和预测，多项采用该技术建立的预测模型，其准确率都达到了70%以上。根据学习策略和互联模式连接方式的不同，ANN分为多种类型，而BP（Back Propogation）神经网络因较其它神经网络具有普遍性强和运算过程清晰等优势，特别适于求解内部机制复杂的问题，应用最为广泛。

提高训练效果，延缓运动疲劳出现和快速从疲劳中恢复是当前运动训练亟待解决的问题，而通过训练场地的环境指标预测运动员的中枢疲劳情况，进而调整相关环境指标以延缓运动员中枢疲劳的出现或使其迅速得以恢复，将可能是提高训练效果的新手段。为此，本研究首次通过BP网络技术构建训练场地综合因素影响下单板U型场地滑雪项目杰出运动员的中枢疲劳预测模型，旨在为其将来的应用提供参考。

1 实验对象和方法

1.1 实验对象

国家单板U型场地滑雪队41名（女17/男24）杰出运动员参与研究。所有运动员均为国家一级以上运动员，平均年龄和平均训练年限分别为20.3±5.2yrs和12.6±5.7yrs。

1.2 实验方法

1.2.1 输入数据的采集

（1）选址。所有评价数据进行采集时，需要选择具有典型性的调查地点。虽然调研得知国家单板U型场地滑雪队有多处训练场地，但日常训练主要集中于哈尔滨体育学院帽儿山滑雪场。为此，本研究选取该滑雪场作为测试地点。

（2）主观调查。采用调查问卷研究影响因素与运动员在训练场地环境下主观感受间的关系，其中声环境主观感受包括声舒适度、主观响度、声喜好等指标，其他环境主观感受包括温度感受、湿度感受、亮度感受和风速感受。具体过程包括：

A.问卷设计：首先提出研究假设，对研究对象进行界定；其次采用结构访谈和无结构访谈相结合的形式对主观响度、声舒适度和声喜好的研究内容进行补充，提出问卷题目的设计方案；最后完成主观响度、声舒适度和声喜好的量表、使用者特征量表和环境调查量表。

B.信度与效度分析：通过5位专家对问卷的效度进行检验，评价结果良好。采用Cronbachα信度进行问卷的信度检验，结果，环境因子信度αl=0.713，声音因子信度α2=0.821，信度满足调查的要求。

C.正式调查：调查以实地发放问卷结合访谈的形式进行，分别于2014年11月、2015年1月和3月对在帽儿山滑雪场训练的杰出单板U型场地滑雪运动员发放121份问卷，回收有效问卷115份，回收率95.0%。调查结果通过SPSS14.0软件录入和进行分类研究。

（3）客观测量。除主观感受外，可能影响中枢疲劳评价结果的一些客观物理指标也被测试，包括声压级、混响时间、温度、湿度、照度及风速。声压级测量使用声级计记录A声级数据，并保证测量位置离U型槽壁面和其它主要反射面不小于Im，距地面1.2m-1.5m，每3-5s记录一次，每个地点记录100个数据，取平均值为测量点的A声级。混响时间使用无指向声源作为声源点，在一定的距离上设置若干个测量点，在声源停止发声时，用高保真录音机记录声压级衰减的过程，并用OldB的软件进行分析。由于测试时滑雪场内的温湿度变化缓慢，因此在调查问卷结束之后，只对每一个点使用温湿度计记录1组温湿度的数据。测量的照度值一般指水平工作面照度。对滑雪场而言，统一选取运动员在U型槽上跃起的平均高度，即男子3.0m，女子2.0m作为水平工作面标准高度，每记录一份问卷之后，对测量点水平工作面照度计量一次。风速测量使用手持式风速仪，测试过程中持续记录，取平均值为测试点的风速。为验证模型准确度，分别对运动员的中枢疲劳情况进行了测试，方法采用闪光融合频率测试，测试时间分别为训练前30min、训练30min、训练60min、训练90min、训练后即刻及训练后30min。

（4）数据分析。采用Matlab7平台进行ANN预测模型的构建。问卷调查及测试获得的主、客观指标的描述采用以平均值±标准差（x±s）；主、客观指标与运动员中枢疲劳的相关性检验采用Pear-son/Spearman相关分析（双尾），各指标在训练及检验组间的差异则采用配对t检验（双尾）。SPSS 14.0软件包统计分析，非常显著性水平与显著性水平分别定为0.01和0.05。

1.2.2 单板U型场地滑雪运动员中枢疲劳ANN模型的构建 以上述与运动员中枢疲劳相关的变量作为输入变量，个体中枢疲劳为输出变量。因样本量有限，在模型分析过程中，80%的数据用于训练而20%数据用于检验；在模型评价过程中，70%的数据用于训练，10%为无效数据，20%的数据用于检验。

（1）隐藏层及节点设计。参考相关文献，ANN模型采用3层结构（1个隐藏层），隐藏节点数范围从5-35，网络的训练次数设定为100-3000次，分别计算训练及检验组的误差与相关系数。

（2）函数选择。ANN的函数主要包括传递函数、训练函数和学习函数。因学习函数对运算的结果影响较小，故仅调整传递函数和训练函数。本研究以纯线性函数PURELIN作为传递函数，训练函数为TRAINLM、TRAINOSS和TRAINCGB这3种经典的Matlab训练函数。隐藏节点数及网络训练次数参照上述：隐藏层及节点设计的结果，分别计算训练及检验组的误差与相关系数。

（3）模型的检验。数据被分为10组，其中8组用于输入数据，1组作为检验数据，1组作为预测数据，以进行模型的过拟合检验。隐藏节点数及网络训练次数参照上述：（1）隐藏层及节点设计的结果，训练模型参照；（2）函数选择的结果，分别计算有/无检验测试下训练及检验组的误差与相关系数。

2 结果与分析

2.1 影响单板U型场地滑雪运动员中枢疲劳的因素

鉴于与ANN模型无关的输人数据会影响预测结果，故输入网络前，需要分析整理出声音、使用者、空间和环境等影响因素与中枢疲劳的关系，如表1所示，16个指标被选为运动员中枢疲劳预测模型的输入变量，输出变量为个体的中枢疲劳。相关检验发现，上述变量中，14个变量与单板U型场地滑雪运动员的中枢疲劳显著相关，故2个与中枢疲劳不相关的要素，A1及A6，在接下来的模型构建中不纳入网络计算。

2.2 单板U型场地滑雪运动员中枢疲劳ANN模型的构建

业已证实，BP神经网络中隐藏层的数量为1层或2层时就可以解决现有的各种分类问题，故本研究选择1个隐藏层的3层结构ANN模型。此外，关于隐藏层的节点数，若数量较少，则网络不能进行训练或降低网络训练的性能；若节点数较多，虽然可能降低网络的训练误差，但训练中也容易出现“过拟合”或导致网络训练时间的提高。

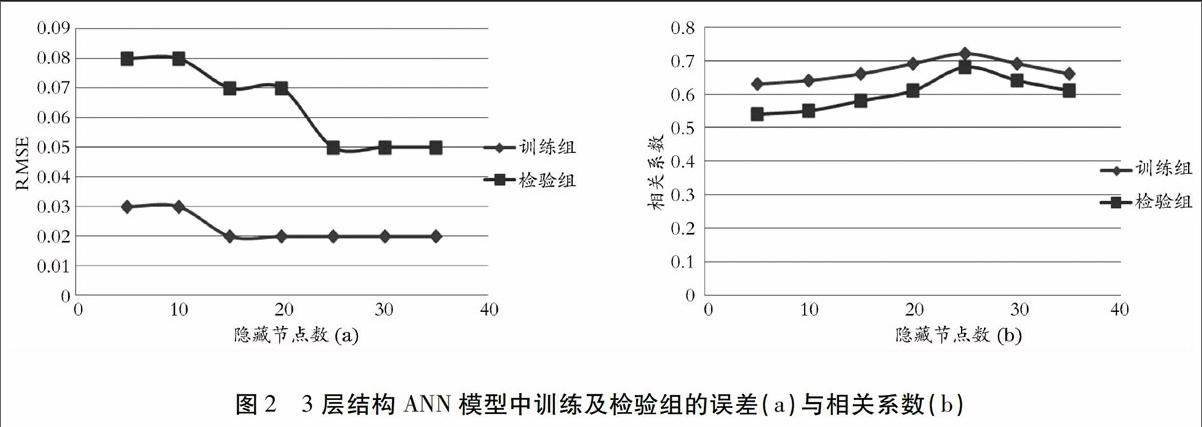
根据隐藏层节点数确定的最基本原则，本研究选择5-35的隐藏节点数范围，ANN模型中训练及检验组的误差与相关系数见图2。由图2（b）可见，当隐藏节点数的变化范围为5-35时，检验组相关系数的变化范围为0.54-0.68，当隐藏节点数从30变为35时，检验组的相关系数由0.64降为0.61，表明隐藏节点数为25是ANN模型在3层结构下的最优节点数。

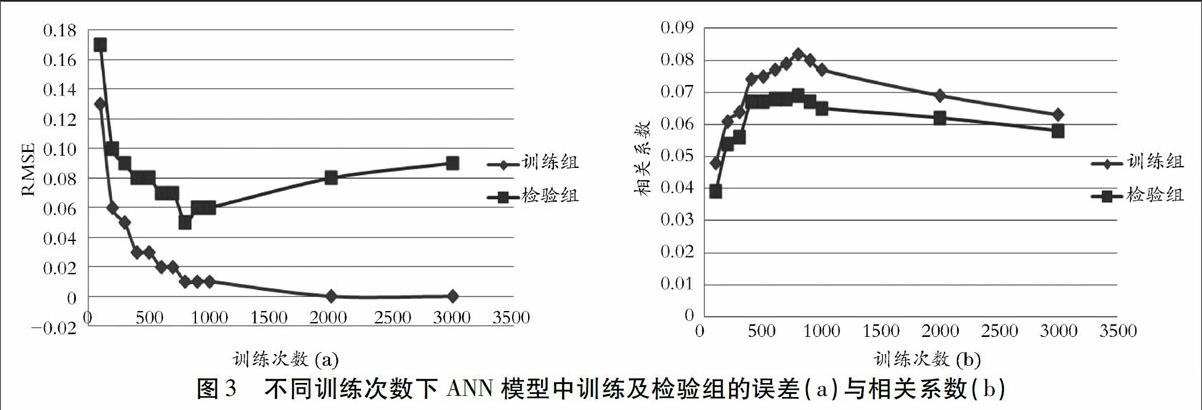
迭代次数是BP人工神经网络的运算次数，增加网络的迭代次数可减少网络的训练误差，但会增加网络的训练时间。为确定合适的迭代次数对网络预测效果的影响，本研究分别训练了100次、200次、300次、400次、500次、600次、700次、800次、900次、1000次、2000次和3000次，不同训练次数下ANN模型中训练及检验组的误差及相关系数见图3。由图3（b）可见，检验组的相关系数在训练次数为100时最低，仅为0.39，随着训练次数的增加，检验组的相关系数逐渐好转，并在训练次数增至400-800时达到0.67-0.69的较好水平。然而，当训练次数继续由900增加至3000的过程中，检验组的相关系数不再增加，而是从0.67逐渐降至0.58，其原因可能是因为网络的迭代次数过多，导致网络的“过拟合”，使其泛化能力降低，即网络从“灵活理解”变为“简单记忆”，使预测的准确率下降，故800次被作为ANN模型的最优训练次数用于模型构建。

根据前面结果，不同训练函数下ANN模型中的隐藏节点数及训练次数均设定为25和800，该模型中训练及检验组的误差与相关系数见图4。

由图可见，TRAINOSS训练函数下ANN模型的训练效果较其他训练函数更好，其检验组的相关系数为0.72，说明选用该训练函数时，网络的收敛速度较慢，训练误差最小；而选用训练函数TRAINM时，网络的收敛速度快，但误差较大，因此在三种训练函数中最不利于ANN模型的训练效果。

根据前面结果，有/无验证测试条件下ANN模型中的隐藏节点数及训练次数均设定为25和800，训练函数采用TRAINOSS，该模型中训练及检验组的标准差与相关系数见表2。由表可见，有验证测试条件下ANN模型的检验组标准差较无验证测试条件下检验组的误差小，表明所有ANN模型在此步均需进行验证测试。

2.3 单板U型场地滑雪运动员中枢疲劳的ANN模型

根据影响运动员中枢疲劳的各变量权重，本研究分别构建了可预测单板U型场地滑雪运动员中枢疲劳的ANN通用模型（General 1和General 2，即G1和G2）和分组模型。ANN通用模型分别选取不同数量的变量，所有可能会影响单板U型场地滑雪运动员中枢疲劳的16个主、客观指标均被选为预测模型G1的输入变量，而G2中的输入变量为14个与运动员中枢疲劳相关的主、客观指标。

此外，由于运动员中枢疲劳受年龄、运动等级和训练年限影响较大，本研究还据此构建了相应的ANN分组模型，即ANN年龄模型（Agel-3，即A1、A2和A3）、ANN运动等级模型（Sport Gradel-3，即SGI、SG2和SG3）及ANN训练年限模型（Training Lengthl-3，即TLI、TL2和TL3）。上述模型的样本分别分为低龄组（<18yrs组）、适龄组（18-22yrs组）和熟龄组（>23yrs组）；国家一级、健将组和国际健将组；以及低年限组（<7yrs组）、中年限组（8-13yrs组）和高年限组（>14yrs组），ANN模型则分别命名为A1、A2、A3；SGI、SG2、SG3；和TLI、TL2、TL3，各模型参数见表3。

在对上述ANN模型进行数轮测试后，获得的最优网络及其预测结果见表4。从中可见，在两种通用ANN模型中，G1模型的预测结果与实际测试结果的相关系数仅为0.44，预测准确度并不理想，而G2模型的预测结果较C1明显好转，其相关系数为0.68，准确度较好，可作为单板U型场地滑雪运动员中枢疲劳的ANN通用预测模型。此外，研究还发现，当将样本按相应标准分组后，ANN年龄模型、ANN运动等级模型和ANN训练年限模型的各组模型预测结果均较好，相关系数均达到0.70以上，预测效果好于通用模型，故可用于单板U型场地滑雪运动员中枢疲劳的分组预测。

3 结论

14个主、客观指标变量与单板U型场地滑雪运动员的中枢疲劳显著相关，2个不相关。在3层结构（1个隐藏层）的ANN模型中，隐藏节点数、训练次数和训练函数分别在25、800和TRAINOSS时效果最优。分别成功构建了可预测训练场地环境综合因素下运动员中枢疲劳情况的ANN通用模型G2和分组模型A1、A2、A3；SG1、SG2、SG3；及TL1、TL2、TL3，并获得了上述模型的最优网络参数及预测结果。