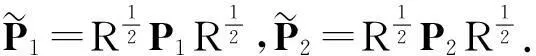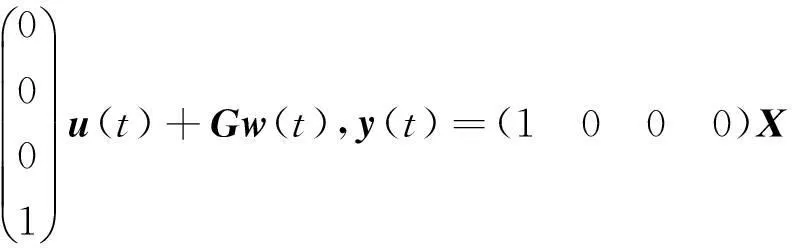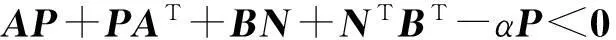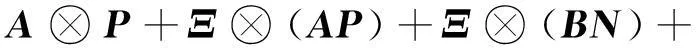基于采样数据卫星姿态的FTB输出反馈控制

薛晓娟　沈艳军

(1. 三峡大学 理学院， 湖北 宜昌　443002； 2. 三峡大学 电气与新能源学院， 湖北 宜昌　443002)



基于采样数据卫星姿态的FTB输出反馈控制

薛晓娟1沈艳军2

(1. 三峡大学 理学院， 湖北 宜昌443002； 2. 三峡大学 电气与新能源学院， 湖北 宜昌443002)

摘要：运用Lyapunov稳定性理论和有限时间有界理论，讨论了基于采样数据卫星姿态的有限时间有界(FTB)输出反馈控制问题.首先给出了使闭环系统满足FTB的充分条件，然后将输出反馈控制器的存在问题转化为线性矩阵不等式(LMI)的可行性问题.最后，仿真实验验证了所设计的控制器的有效性和可行性．

关键词：卫星姿态；线性系统；有限时间有界；输出反馈控制

有限时间有界是目前控制届的研究热点之一．1961年Peter Dorato提出了“短时间稳定(Short Time Stability)”的概念[1]，有限时间控制问题开始成为人们关注的研究热点．在系统受外部扰动情况下，Amato[2]提出了有限时间有界(FTB)的概念．随后，他们等[3]讨论了一类带有时变参数不确定性和定常外部扰动的线性系统的有限时间控制问题，提出了系统是FTB的充分条件，然后设计了状态反馈控制器，将控制器的存在问题转化为LMIs可行性问题．同时，输出反馈FTB控制器也得到研究[4]，进一步改进结果见文献[5-6]．文献[7]讨论了具有范数有界的外部干扰的线性变参数系统的有限时间控制问题，文献[8-9]将有限时间控制问题拓展到奇异系统．Ichihara等人分别给出连续时间系统[10]和离散时间系统[11]带有输入限制的有限时间控制问题，更多结果见文献[12-14]．

从上述的研究成果可以看出，基于采样数据有限时间控制问题的研究成果很少，因此，在文献[6]的基础上，本文将有限时间有界引入到基于采样数据线性系统中，通过Lyapunov稳定性理论和有限时间有界理论，讨论了基于采样数据卫星姿态的FTB输出反馈控制问题，将控制器的存在问题转化为线性矩阵不等式的可行性问题．最后，仿真实验验证了所设计的控制器的有有效性和可行性．

1基础知识

考虑如下线性系统

其中，矩阵A∈Rn×n，G∈Rn×l，状态向量x(t)∈Rn，外部扰动w(t)∈Rl满足

首先给出以下定义和引理：

定义1(FTB)称线性系统(1)在外部扰动w(t)满足(2)的条件下，关于(c1，c2，T，R，h，d)(00)是FTB的，如果

其中h代表采样周期．

引理1对任意的正定矩阵M∈Rn×n，变量γ>0以及向量函数ω：[0，γ]→Rn，那么下面的不等式成立：

2主要结果

考虑如下卫星姿态控制问题[15]，图1展示了某卫星及其双体模型的简图．在图1(a)中，卫星姿态θ1表示主卫星关于行星的角度，θ2表示行星传感器和仪表组织间的角度，图1(b)中展示了卫星等效机械系统图，在该图中，传感器被安装到与θ2有关的硬盘上．对卫星来说，假定两个主体通过在图1中展示的带有转矩矩阵的弹簧k和粘滞阻尼常数b连接．

图1　卫星及其双体模型简图

模型的方程式为：

其中，Tc是在主体上的控制转矩，J1、J2为实常数．

令

则可得：

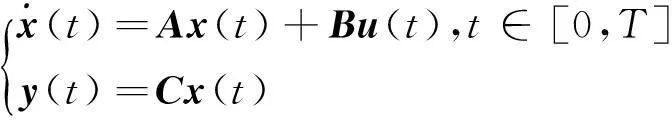
在卫星系统中，不可避免地存在一些摩擦等外部因素，因此，在上述系统中，考虑外部扰动，得到

其中，B∈Rn×m，C∈Rp×n，x(t)，w(t)，A，G前面已给出，下面将在这个形式下讨论该系统的有限时间有界问题．

假设1：假设输出y(t)在tk是可测的，其中tk表示采样时刻且满足tk+1=tk+h．

本文目的是基于采样数据设计如下输出反馈控制器

使得闭环系统是FTB的，由式(5)～(7)可得

考虑状态转换

得如下闭环系统

其等价形式为

定理1存在观测器增益L和形式如(7)的控制器，使得闭环系统(10)关于(c1，c2，T，h，R，d)是FTB的，如果存在矩阵P1∈Rn×n>0，P2∈Rl×l>0，以及非负α和3个正数λa，λb，λc满足

证明：构造如下Lyapunov泛函

其中，

沿着系统(11)的状态对V(z(t))求导数，并由引理1，得

其中，

另一方面，由式(12)可以得到

由上式可以得到

在式(19)两边同时乘以e-αt，并在区间t∈[0，T]进行积分，得

由于α≥0，可得到

从式(21)中可以得到

同时，从式(15)得到

从式(16)得到

故，V2(z(0))为

将式(23)和式(24)代入式(22)，得

且

由式(25)和式(26)，得到

对于所有的t∈[0，T]，由条件(13)得到，xT(t)Rx(t)

推论1存在观测器增益L和形式(7)的控制器，使系统(13)关于(c1，c2，T，h，R，d)是FTB的，如果存在矩阵P1∈Rn×n>0，P2∈Rl×l>0，以及非负α和3个正数λa，λb，λc满足：

证明：通过Schur补定理，由(12)可以得到

注1：LMI条件(28)、(29)、(30)、(31)的成立依赖于c2，满足(28)、(29)、(30)、(31)的c2的最小上界可以通过求解下面关于P1，P2，c2，K，L的优化问题求得．

3仿真实例

在本节中，使用下面的例子来证明通过输出反馈提出的采样控制器的正确性和有效性.

例1：在上述卫星姿态控制问题的系统(5)中，选取k=0.091，b=0.0036以及J1=1，J2=0.1，则得

令c1=1，d=1，T=5，R=I，其中I为适当阶数的单位阵，初始条件设为[0.1；0.1；0.1；0.1]，并且选取外部扰动为w(t)=0.5sin5t．

接下来分两步求解状态反馈控制器K以及观测器增益L．

由文献[16]可知，在闭环系统的区域极点配置复平面有界区域D的范围内，存在一个状态反馈控制器K当且仅当存在一个适合维数的矩阵S满足

因此，假设

同时求解推论1和最小值问题(33)．

第1步：设计K

存在一个非负的常数α，一个正定矩阵P和一个矩阵N满足式(35)～(37)：

在求解式(35)～(37)时，需要首先给出一个α的值来保证式(35)～(37)是一组线性矩阵不等式.在这种情况下，需要将闭环系统极点配置到上述定义的区域D的范围内，因此，闭环系统是渐近稳定的，同时，选取α=0，使用MatlabLMIToolbox[17]，求得

第2步：设计L

存在一个非负的常数α，3个正数λa，λb，λc，对称矩阵P1，P2和一个矩阵M满足式(39)～(43)：

再次使用MatlabLMIToolbox，得到

[-3.763 3 -5.791 6 -4.907 8 -1.105 7]T

同时得到c2=1.25．

图2　例1中状态向量在[0，T]上的轨迹

在图2中，给出的是例1中状态向量在[0，T]上的轨迹；由图3可以看到例1中xT(t)Rx(t)在[0，T]上的轨迹，且其轨迹一直在c2的下方，说明在[0，T]上，在控制器的作用下，xT(t)Rx(t)

图3　例1中xT(t)Rx(t)在[0，T]上的轨迹

4结语

本文运用Lyapunov稳定性理论和有限时间有界理论，讨论了基于采样数据卫星姿态的有限时间有界(FTB)输出反馈控制问题.首先给出了使闭环系统满足FTB的充分条件，然后将输出反馈控制器的存在问题转化为线性矩阵不等式(LMI)的可行性问题.最后，仿真实验验证了所设计的控制器的有效性和可行性．

参考文献：

[1]Dorato P． Short Time Stability in Linear Time-varying Systems[C]． Proc of the IRE International Convention Record Part, 1961(4)： 83-87．

[2]Amato F, Ariola M, Abdallah C T． Dynamic Output Feedback Finite-time Control of LTI Systems Subject to Parametric Uncertainties and Disturbances[C]． Kalsruhe, In Proc. European control conference, 1999：1176-1180．

[3]Amato F, Ariola M, Dorato P． Finite-time Control o f Linear Systems Subject to Parametric Uncertainties and Disturbances[J]． Automatica, 2001. 37： 1459-1463．

[4]Amato F, Ariola M, Cosentino C． Finite Time Control via Output Feedback： A General Approach[C]． Proceedings of the 42nd IEEE Conference on Decision and Control, Maui, Hawaii USA, 2003, 350-355．

[5]Amato F, Ariola M, Cosentino C． Finite-Time Control of Linear Time-Varying Systems via Output Feedback[C]． Proceedings of the American Control Conference, Portland, 2005, 4722-4726．

[6]Amato F, Ariola M, Cosentino C． Finite-Time Stabilization via Dynamic Output Feedback[J]． Automatica, 2006, 42(2)： 337-342．

[7]Shen Y． Finite-time Control of Linear Parameter-varying Systems with Norm-bounded Exogenous Disturbance[J]． Control Theory Appl , 2008,6(2)：184-188．

[8]冯俊娥,吴臻,孙甲冰．具有干扰输入的不确定奇异系统有限时间控制器设计[C]．第五届全球智能控制与自动化大会论文集.杭州：浙江大学出版社,2004：1002-1006．

[9]孙甲冰,程兆林．一类不确定线性奇异系统的有限时间控制问题[J]．山东大学学报：理学版,2004,39(2)：101-106．

[10] Ichihara H, Katayama H． Finite-Time Control for Linear Systems with Input Constraints[C]． Proceedings of the American Control Conference, Hyatt Regency Riverfront, St, Louis, MO, USA, 2009： 476-481．

[11] Ichihara H, Katayama H． Finite-Time Control for Linear Discrete-Time Systems with Input Constraints[C]． Proceedings of the American Control Conference, Hyatt Regency Riverfront, St, Louis, MO, USA, 2009,1171-1176．

[12] Amato F, Ambrosino R, Ariola M, et al． Finite-time Stability of Linear Time-varying Systems with Jumps[J]． Automatica, 2009, 45：1354-1358．

[13] Amato F, Ariola M, Cosentino C． Finite-time Control of Discrete-time Linear Systems： Analysis and Design Conditions[J]． Automatica, 2010, 46(5)： 919-924．

[14] Amato F, Tommasi G, Pironti A． Necessary and Sufficient Conditions for Finite-time Stability of Impulsive Dynamical Linear Systems[J]． Automatica, 2013, 49：2546-2550．

[15] Franklin G J，Powell J D， Emami-Naeini A． Feedback Control of Dynamic Systems[M]． Fifth Edition． 北京：人民邮电出版社, 2007,7 ： 550-552．

[16] Chilali M, Gahinet P, Apkarian P． Robust Pole Placement in LMI Regions[J]． IEEE Transactions on Automatic Control, 1999,44：2257-2270．

[17] Gahinet P, Nemirovski A, Laub A J, et al． LMI Control Toolbox. Natick[M]． MA： The Mathworks Inc， 1995．

[责任编辑张莉]

Output Feedback FTB Control for Satellite Attitude

Based on Sampled-data Measurement

Xue Xiaojuan1Shen Yanjun2

(1. College of Science, China Three Gorges Univ., Yichang 443002, China； 2. College of Electrical Engineering & Renewable Energy, China Three Gorges Univ., Yichang 443002, China)

AbstractBy using the Lyapunov theory and finite time boundedness (FTB) theory, an output feedback controller was designed for satellite attitude based on sampled-data measurement. Sufficient conditions are presented to ensure that the closed-loop system is FTB. Then, the existence of the controller can be transformed into the feasibility problem of the linear matrix inequalities(LMIs). Finally, an example is given to illustrate the validity and effectiveness of the methodology.

Keywordssatellite attitude；linear system；finite time boundedness；output feedback control

基金项目：国家自然科学基金资助项目(51275273)

收稿日期：2015-06-07

中图分类号：P134.3

文献标识码：A

文章编号：1672-948X(2015)06-0085-06

DOI：10.13393/j.cnki.issn.1672-948X.2015.06.018

通信作者：沈艳军(1970-)，男，教授，博士，主要从事鲁棒控制、人工神经网络、智能控制等的研究．E-mail：shenyj@ctgu.edu.cn